第6章 一元一次方程素养提优卷(含解析)
文档属性
| 名称 | 第6章 一元一次方程素养提优卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 646.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 00:00:00 | ||
图片预览




文档简介
第6章 一元一次方程 素养提优卷
考试时间:100分钟 满分:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
请点击修改第I卷的文字说明
一、单选题
1.下列方程中,解是的方程是( )
A. B. C. D.
2.下列说法正确的是( )
A.如果,那么 B.如果,那么
C.如果,那么 D.如果,那么
3.若关于的方程是一元一次方程,则此方程的解是( )
A. B. C. D.
4.当的取值不同时,整式(其中是常数)的值也不同,具体情况如表所示:
0 1
4 2 0
则关于的方程的解为( )
A. B. C. D.
5.如果方程和方程的解互为相反数,那么的值为( )
A. B. C. D.
6.小亮在做作业时,不小心将墨水洒在了作业纸上,导致方程=x中的一个常数被污染,同桌说正确答案是,则被污染的常数是( )
A.6 B.5 C.4 D.3
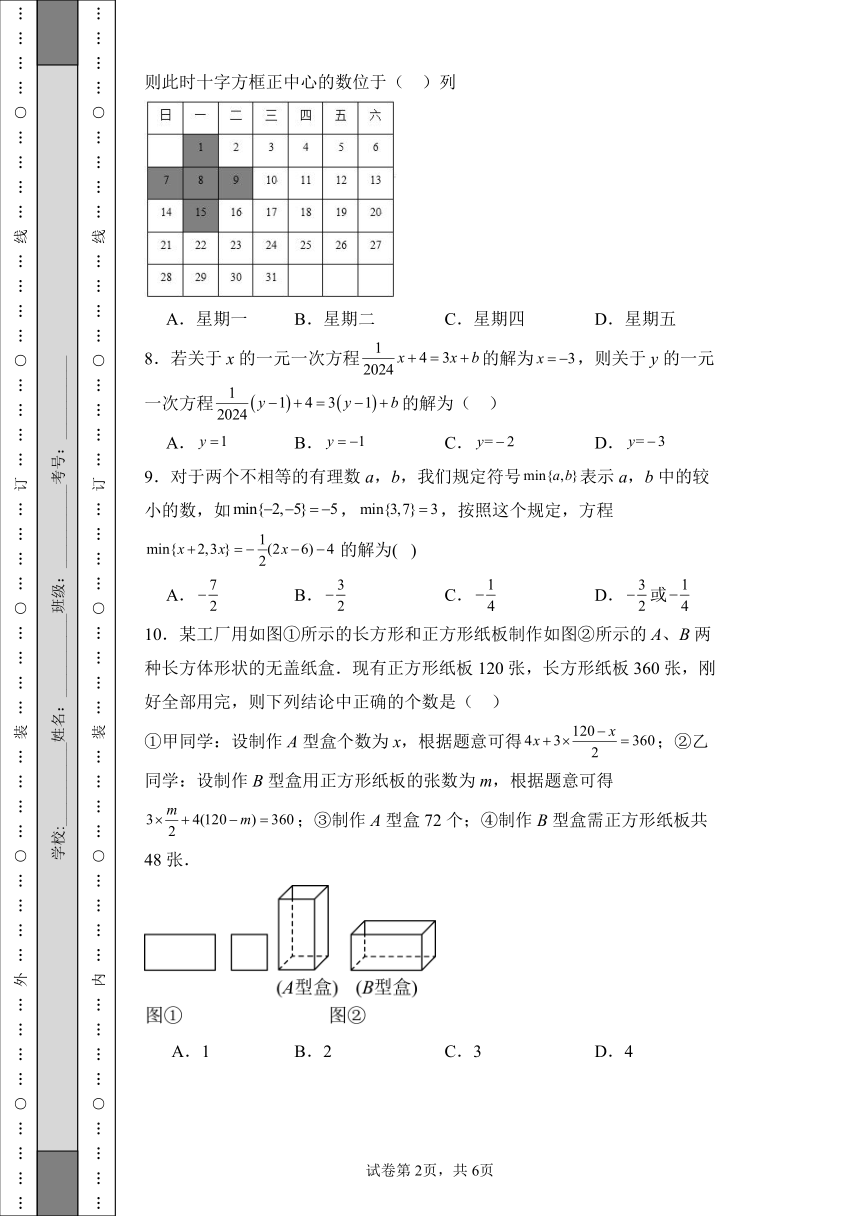
7.如图,在2024年1月的日历中,用带阴影的十字方框覆盖其中5个数字,例如:1,7,8,9,15.现在移动十字方框,使其覆盖的5个数之和等于115,则此时十字方框正中心的数位于( )列
A.星期一 B.星期二 C.星期四 D.星期五
8.若关于x的一元一次方程的解为,则关于y的一元一次方程的解为( )
A. B. C. D.
9.对于两个不相等的有理数a,b,我们规定符号表示a,b中的较小的数,如,,按照这个规定,方程的解为( )
A. B. C. D.或
10.某工厂用如图①所示的长方形和正方形纸板制作如图②所示的A、B两种长方体形状的无盖纸盒.现有正方形纸板120张,长方形纸板360张,刚好全部用完,则下列结论中正确的个数是( )
①甲同学:设制作A型盒个数为x,根据题意可得;②乙同学:设制作B型盒用正方形纸板的张数为m,根据题意可得;③制作A型盒72个;④制作B型盒需正方形纸板共48张.
A.1 B.2 C.3 D.4
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
11.列方程表示“的倍与的和等于”: .
12.若方程和方程的解相同,则的值为 .
13.我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.”其大意为:有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;将绳索对半折后再去量竿,就比竿短5尺.如果设绳索长为x尺,则列一元一次方程是 .
14.如果两个一元一次方程的解互为倒数,我们就称这两个方程为“友好方程”.例如,方程和方程为“友好方程”.若关于的方程与方程是“友好方程”,则 .
15.如图,在的方格中,每个小方格的边长为1且标记数字,在方格中画阴影正方形.现规定被阴影正方形全部覆盖的小方格,其数值之和记为m,部分覆盖的小方格,其数值之和的一半记为n.以图1中阴影正方形为例,.若在图2中画一个面积为5的阴影正方形(顶点均在格点上),且,则m的值为 .
三、解答题
16.已知关于x的方程是一元一次方程.
(1)求m的值;
(2)已知:是该一元一次方程的解,求n的值.
17.解方程:
(1);(2).
18.十八世纪最杰出的瑞士数学家欧拉,最先把关于的多项式用符号“”表示,如果.例:当时,.
(1)当时,求的值.
(2)当时,求的值.
19.在学习《求解一元一次方程》之后,老师在黑板上出了一道解方程的题,下面是小乐同学的解题过程,请仔细阅读并完成相应的任务.
解:………………第一步 …………………第二步 ………………第三步 ……………………………第四步 ……………………………第五步
任务一:填空:
①以上解题过程中,第一步的变形的依据是 ;第二步去括号时依据的运算律是 ;
②以上解题过程中从第 步开始出现错误,这一步错误的原因是 ;
③请直接写出该方程的正确解: ;
任务二:除纠正上述错误外,请你根据平时的学习经验,就解一元一次方程还需要注意的事项给同学们提一条建议.
20.某飞镖游戏的靶盘如图所示,游戏规定:若投出靶盘外则视为脱靶,计分规则如下:
投中位置 A区 B区 脱靶
一次计分 3分 1分 分
小颖玩了两局游戏,每局投10次飞镖.
(1)在第一局中,小颖投中A区4次,B区2次,脱靶4次,求小颖本局得分;
(2)第二局中,小颖投中A区m次,B区3次,其余全部脱靶,小颖称本局得分比第一局高11分.请你通过计算判断小颖的说法是否正确.
21.观察下列三个等式:,我们称使等式成立的一对有理数a,b为“有趣数对”,记为,例如数对都是“有趣数对”,请回答下列问题:
(1)数对是“有趣数对”吗?试说明理由.
(2)若是“有趣数对”,求a的值.
(3)若是“有趣数对”,求的值.
22.小王自主创业开了一家服装店,经营一段时间后,小王发现每件进价为200元的A种服装,按标价的八折出售时的利润率为.
(1)求A种服装的标价为多少元?
(2)已知B种服装的进价为300元,小王售完两种服装后,又以原来的价格购进A,B两种服装共110件,所用资金为28000元.
①求购进的A,B两种服装各多少件?
②由于小王对市场需求了解不清楚,换季时,A种服装虽已全部售出,但B种服装按标价400元只售出了10件,为了尽快回笼资金,小王决定对剩余的B种服装打折处理,在B种服装恰好保本的情况下,剩余的B种服装打几折处理?
23.如图,某动力科学研究实验基地内装有一段长为的笔直轨道,现将长度为的金属滑块在上面往返滑动一次,滑动开始前,滑块左端与点A重合,滑动过程由三个阶段组成:
1.滑块以的速度沿方向匀速滑动,当滑块的右端与点B重合时,滑动停止.
2.滑块停顿.
3.滑块以小于的速度沿方向匀速返回,当滑块的左端与点A重合时,滑动停止.设滑动时间为时,滑块左端离点A的距离为,右端离点B的距离为,
(1)当时,求的值.
(2)整个滑动过程总用时(含停顿的时间),请根据所给条件解决下列问题:
①求滑块返回的速度.
②记,若,求t的值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】本题考查了解一元一次方程及一元一次方程的解,熟练掌握解一元一次方程的步骤是解题的关键.
【详解】解:A、的解是,故此选项不符合题意;
B、的解是,故此选项符合题意;
C、的解是,故此选项不符合题意;
D、的解是,故此选项不符合题意;
故选:B.
2.B
【分析】题目主要考查等式的性质,根据等式的性质逐一判断即可得答案,熟练掌握等式的基本性质是解题关键.
【详解】解:A、C、若,等式变形错误,故A、C不符合题意;
B、如果,那么,正确,故B符合题意;
D、如果,那么,故D不符合题意.
故选:B.
3.A
【分析】本题考查了一元一次方程的定义,以及一元一次方程的求解,一元一次方程指只含有一个未知数、未知数的最高次数为1且两边都为整式的等式.据此即可求解.
【详解】解:由题意得:,
∴
原方程为:,
解得:,
故选:A
4.D
【分析】本题考查一元一次方程的解,解题的关键是理清表格中数据的含义.方程整理为,根据表格确定出所求方程的解.
【详解】解:,
,
从表格中观察:当时,,
故选:D.
5.C
【分析】本题主要考查了一元一次方程的解和解法,先按照解一元一次方程的一般步骤,求出已知条件中两个方程的解,然后根据两个方程的解是互为相反数,列出关于的方程,解方程即可.解题关键是熟练掌握一元一次方程解的定义和解一元一次方程的一般步骤.
【详解】解: 由解得:,
,
方程两边同时乘得:,
去括号得:,
移项得:,
合并得:,
方程和方程 的解互为相反数,
,
,
,
故选:C.
6.C
【分析】本题主要考查了一元一次方程的解以及解一元一次方程,把代入,得出关于m的一元一次方程,解方程即可求解.
【详解】解:设常数项为m,则原方程为:,
把代入,
则方程变成:,
整理得:,
解得:,
故选:C.
7.B
【分析】本题主要考查了一元一次方程的应用,解题的关键是根据题意列出方程,准确计算.设中心数为x,根据5个数之和等于115,列出方程,解方程即可.
【详解】解:设中心数为x,根据题意得:
,
解得:,
∴此时十字方框正中心的数位于星期二这一列,
故选:B.
8.C
【分析】本题考查了一元一次方程的解的定义,熟记使一元一次方程左右两边相等的未知数的值叫做一元一次方程的解是解题的关键.
根据题中两个方程的关系,可知,即可求出y的值.
【详解】解:∵方程的解为,
∴方程的解满足,
解得:.
故选:C.
9.C
【分析】本题考查了一元一次方程的求解,分类讨论①若,即:时②若,即:时两种情况即可求解.
【详解】解:①若,即:时:
原方程为:,
解得:;
②若,即:时:
原方程为:,
解得:(舍去)
故选:C
10.D
【分析】观察图形可知,A型纸盒需要4个长方形纸板,1个正方形纸板,B型纸盒需要3个长方形纸板和2个正方形纸板,设A型盒子个数为x个,可得A型纸盒需要长方形纸板的数量和B型纸盒需要长方形纸板的数量,可列出方程对①进行判断;设B 型盒中正方形纸板的个数为m个,可得B型纸盒需要长方形纸板的数量和A型纸盒需要长方形纸板的数量,可列出方程对②进行判断;设制作A 型盒子a个,B型盒子b个,根据长方形纸板360张,正方形纸板120张,可得出方程组,解之即可得出a,b值,进而可对③④进行判断.
【详解】解:设A型盒子个数为x个,则A型盒子需要长方形纸板张,正方形纸板x张,
∵B型纸盒需要2个正方形纸板,
∴可制作B型纸盒的数量为个,需要长方形纸板张,
∴,故①正确;
设B 型盒中正方形纸板的个数为m个,则B型纸盒有个,需要长方形纸板张,A型盒子有个,
∴,故②正确;
设制作A 型盒子a个,B型盒子b个,
则,解得,
∴A型盒子有72个,B型纸盒有24个,
∴B型纸盒中正方形纸板48个,
故③④正确;
故正确的个数有4个.
故选:D.
【点睛】本题考查了由实际问题抽象出一元一次方程以及二元一次方程组的应用,找准等关系,正确列出一元一次方程(或二元一次方程组)是解题的关键.
11.
【分析】本题考查了列一元一次方程,根据题意直接列出一元一次方程即可求解,理解题意是解题的关键.
【详解】解:由题意可得,,
故答案为:.
12.2
【分析】此题主要考查了一元一次方程解的定义.解答此题的关键是熟知方程组有公共解的含义,考查了学生对题意的理解能力.
先求方程的解,再代入,求得的值.
【详解】解:解方程,得,
把代入,
得:,
解得.
故答案为:2.
13.
【分析】本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次方程是解题的关键.设绳索长x尺,则竿长尺,根据“将绳索对半折后再去量竿,就比竿短5尺”,即可得出关于x的一元一次方程,此题得解.
【详解】解:设绳索长x尺,则竿长尺,
依题意,得:,
故答案为:.
14.
【分析】本题考查解一元一次方程,解方程与方程,根据题中“友好方程”定义,列方程求解即可得到答案,熟练掌握一元一次方程解法是解决问题的关键.
【详解】解:解得;
解得;
关于的方程与方程是“友好方程”,
,解得,
故答案为:.
15.12
【分析】本题考查的是图形的变化规律,关键是通过图1中面积为10的阴影正方形,分析出图2中面积为5的阴影正方形,被全部覆盖的小方格有1个,被部分覆盖的小方格有8个;然后列式求解即可.
图1中阴影正方形的面积为10,被全部覆盖的小方格有4个,被部分覆盖的小方格有10个;则面积为5的阴影正方形,被全部覆盖的小方格有1个,被部分覆盖的小方格有8个;被全部覆盖的小方格数值即为m,被部分覆盖的小方格,数值分别为、、、、、、、;因,将式子进行化简计算即可.
【详解】解:如图所示,
面积为5的阴影正方形,被全部覆盖的小方格有1个,被部分覆盖的小方格有8个;
被全部覆盖的小方格数值即为m,被部分覆盖的小方格,数值分别为;
因为,即,
,
解得:.
故答案为:12.
16.(1)
(2)
【分析】本题考查一元一次方程的定义,方程的解.
(1)根据一元一次方程的定义可得,,求解即可;
(2)把代入方程,求解即可.
【详解】(1)∵关于x的方程是一元一次方程,
∴且
∴;
(2)由(1)得,该一元一次方程为,
∵是该方程的解,
∴,
∴.
17.(1)
(2)
【分析】本题主要考查解一元一次方程,去分母、去括号、移项、合并同类项、系数化为1,这仅是解一元一次方程的一般步骤,针对方程的特点,灵活应用,各种步骤都是为使方程逐渐向形式转化.
依次去括号、移项、合并同类项、系数化为1可得;
依次去括号、移项、合并同类项、系数化为1可得.
【详解】(1)解:
移项得:
合并同类项得:
系数化为1,得:
(2)解:
去括号得:
移项得:
合并同类项得:
系数化为1,得:
18.(1)
(2)x的值为或
【分析】此题考查了新定义运算,熟练掌握代数式的求值和解一元一次方程是解题的关键.
(1)根据题意代入求值即可;
(2)根据题意列出方程,解方程即可.
【详解】(1)解:当时,
.
(2)当时,即,
当时有:
,
;
当时有:
,
,
∴当时,x的值为或.
19.任务一:①等式的基本性质;乘法分配律;②三;移项时没有变号;③;任务二:①去分母时要给每一项乘以分母的最小公倍数数,特别是常数项是易错点;②去括号时,如果括号外是“” 号,括号内每一项都要变号;③移项时,注意移动项的符合的变化(不唯一).
【分析】本题主要考查了解一元一次方程,掌握解一元一次方程的基本步骤以及注意事项是解题的关键.
任务一:根据解一元一次方程的基本步骤逐步分析、判定即可解答;
任务二:结合解一元一次方程的经验,总结注意事项即可.
【详解】解:任务一:
①以上解题过程中,第一步的变形的依据是等式的基本性质;第二步去括号时依据的运算律是乘法分配律;
②以上解题过程中从第三步开始出现错误,这一步错误的原因是移项时没有变号;
由,
,
,
,
③该方程的正确解:;
故答案为:①等式的基本性质;乘法分配律;②三;移项时没有变号;③;
任务二:解一元一次方程需要注意以下事项:①去分母时要给每一项乘以分母的最小公倍数数,特别是常数项是易错点;②去括号时,如果括号外是“” 号,括号内每一项都要变号;③移项时,注意移动项的符合的变化
20.(1)小颖本局得分为6分
(2)小颖的说法不正确,理由见解析
【分析】本题主要考查有理数混合运算和一元一次方程的应用,
通过投中的区和各区的分数即可求得得分;
首先求得投中各区的次数,根据各区的分数列出本局得分代数式,再结合题意列出方程求解判断正确与否;
【详解】(1)解:∵A区4次,B区2次,脱靶4次,
∴(分).
则小颖本局得分为6分.
(2)由题意,得本局脱靶次数为:(次).
本局得分:(分).
∵小颖称本局得分比第一局高11分.
∴,解得,与题意不符.
所以,小颖的说法不正确.
21.(1)不是,理由见解析;
(2);
(3).
【分析】本题考查有理数的运算,一元一次方程的实际应用,代数式求值,理解“有趣数对”的定义,是解题的关键.
(1)根据“有趣数对”的定义,进行判断即可;
(2)根据“有趣数对”的定义,列出方程进行求解即可;
(3)先根据“有趣数对”的定义,得到,利用整体代入法求代数式的值即可.
【详解】(1)解:不是,理由如下,
∵,,,
∴数对不是“有趣数对”;
(2)∵是“有趣数对”,
∴
解得:;
(3)∵是“有趣数对”
∴,
即,
.
22.(1)A种服装的标价为300元
(2)①A种服装购进50件,B种服装购进60件;②剩余的B种服装打七折处理
【分析】本题考查了一元一次方程的应用;
(1)设A种服装的标价为元,根据利润率的计算方法列方程求解即可;
(2)①设购进的A种服装有件,则购进的B种服装有件,根据购进A,B两种服装共110件,所用资金为28000元列方程求解即可;
②设剩余的B种服装打折处理,根据只售的10件的金额加上处理部分的进而等于B种服装进货总额,列方程求解即可.
【详解】(1)解:设A种服装的标价为元,
由题意得:,
解得:,
答:A种服装的标价为300元;
(2)①设购进的A种服装有件,则购进的B种服装有件,
由题意得:,
解得:,
则,
答:A种服装购进50件,B种服装购进60件;
②设剩余的B种服装打折处理,
由题意得:,
解得:,
答:剩余的B种服装打七折处理.
23.(1)
(2)或
【分析】本题考查了一元一次方程的应用:
(1)根据时间等于路程除以速度,可知当时,滑块右端刚好与点B重合,即可求得答案;
(2)①先求得返回所用的时间,根据速度等于路程除以时间求解即可;②分两种情况讨论:1)当滑块从左向右滑动,2)当滑块从右向左滑动,根据题意列出方程求解即可.
【详解】(1)解:轨道长为,长度为的滑块从点A到点B的速度为,
第一阶段所用的时间为,
当时,滑块右端刚好与点B重合,;
(2)解:①整个过程用时,当滑块右端与点B重合时,滑块停顿,
第三阶段所用的时间为.
滑块返回的速度为.
②分析可得:,当时,显然第二阶段时不满足,所以分两种情况:
1)当滑块从左向右滑动,即时,,,,,解得;
2)当滑块从右向左滑动,即时,,,,解得.
综上所述,当或时,.
答案第1页,共2页
答案第1页,共2页
考试时间:100分钟 满分:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
请点击修改第I卷的文字说明
一、单选题
1.下列方程中,解是的方程是( )
A. B. C. D.
2.下列说法正确的是( )
A.如果,那么 B.如果,那么
C.如果,那么 D.如果,那么
3.若关于的方程是一元一次方程,则此方程的解是( )
A. B. C. D.
4.当的取值不同时,整式(其中是常数)的值也不同,具体情况如表所示:
0 1
4 2 0
则关于的方程的解为( )
A. B. C. D.
5.如果方程和方程的解互为相反数,那么的值为( )
A. B. C. D.
6.小亮在做作业时,不小心将墨水洒在了作业纸上,导致方程=x中的一个常数被污染,同桌说正确答案是,则被污染的常数是( )
A.6 B.5 C.4 D.3
7.如图,在2024年1月的日历中,用带阴影的十字方框覆盖其中5个数字,例如:1,7,8,9,15.现在移动十字方框,使其覆盖的5个数之和等于115,则此时十字方框正中心的数位于( )列
A.星期一 B.星期二 C.星期四 D.星期五
8.若关于x的一元一次方程的解为,则关于y的一元一次方程的解为( )
A. B. C. D.
9.对于两个不相等的有理数a,b,我们规定符号表示a,b中的较小的数,如,,按照这个规定,方程的解为( )
A. B. C. D.或
10.某工厂用如图①所示的长方形和正方形纸板制作如图②所示的A、B两种长方体形状的无盖纸盒.现有正方形纸板120张,长方形纸板360张,刚好全部用完,则下列结论中正确的个数是( )
①甲同学:设制作A型盒个数为x,根据题意可得;②乙同学:设制作B型盒用正方形纸板的张数为m,根据题意可得;③制作A型盒72个;④制作B型盒需正方形纸板共48张.
A.1 B.2 C.3 D.4
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
11.列方程表示“的倍与的和等于”: .
12.若方程和方程的解相同,则的值为 .
13.我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.”其大意为:有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;将绳索对半折后再去量竿,就比竿短5尺.如果设绳索长为x尺,则列一元一次方程是 .
14.如果两个一元一次方程的解互为倒数,我们就称这两个方程为“友好方程”.例如,方程和方程为“友好方程”.若关于的方程与方程是“友好方程”,则 .
15.如图,在的方格中,每个小方格的边长为1且标记数字,在方格中画阴影正方形.现规定被阴影正方形全部覆盖的小方格,其数值之和记为m,部分覆盖的小方格,其数值之和的一半记为n.以图1中阴影正方形为例,.若在图2中画一个面积为5的阴影正方形(顶点均在格点上),且,则m的值为 .
三、解答题
16.已知关于x的方程是一元一次方程.
(1)求m的值;
(2)已知:是该一元一次方程的解,求n的值.
17.解方程:
(1);(2).
18.十八世纪最杰出的瑞士数学家欧拉,最先把关于的多项式用符号“”表示,如果.例:当时,.
(1)当时,求的值.
(2)当时,求的值.
19.在学习《求解一元一次方程》之后,老师在黑板上出了一道解方程的题,下面是小乐同学的解题过程,请仔细阅读并完成相应的任务.
解:………………第一步 …………………第二步 ………………第三步 ……………………………第四步 ……………………………第五步
任务一:填空:
①以上解题过程中,第一步的变形的依据是 ;第二步去括号时依据的运算律是 ;
②以上解题过程中从第 步开始出现错误,这一步错误的原因是 ;
③请直接写出该方程的正确解: ;
任务二:除纠正上述错误外,请你根据平时的学习经验,就解一元一次方程还需要注意的事项给同学们提一条建议.
20.某飞镖游戏的靶盘如图所示,游戏规定:若投出靶盘外则视为脱靶,计分规则如下:
投中位置 A区 B区 脱靶
一次计分 3分 1分 分
小颖玩了两局游戏,每局投10次飞镖.
(1)在第一局中,小颖投中A区4次,B区2次,脱靶4次,求小颖本局得分;
(2)第二局中,小颖投中A区m次,B区3次,其余全部脱靶,小颖称本局得分比第一局高11分.请你通过计算判断小颖的说法是否正确.
21.观察下列三个等式:,我们称使等式成立的一对有理数a,b为“有趣数对”,记为,例如数对都是“有趣数对”,请回答下列问题:
(1)数对是“有趣数对”吗?试说明理由.
(2)若是“有趣数对”,求a的值.
(3)若是“有趣数对”,求的值.
22.小王自主创业开了一家服装店,经营一段时间后,小王发现每件进价为200元的A种服装,按标价的八折出售时的利润率为.
(1)求A种服装的标价为多少元?
(2)已知B种服装的进价为300元,小王售完两种服装后,又以原来的价格购进A,B两种服装共110件,所用资金为28000元.
①求购进的A,B两种服装各多少件?
②由于小王对市场需求了解不清楚,换季时,A种服装虽已全部售出,但B种服装按标价400元只售出了10件,为了尽快回笼资金,小王决定对剩余的B种服装打折处理,在B种服装恰好保本的情况下,剩余的B种服装打几折处理?
23.如图,某动力科学研究实验基地内装有一段长为的笔直轨道,现将长度为的金属滑块在上面往返滑动一次,滑动开始前,滑块左端与点A重合,滑动过程由三个阶段组成:
1.滑块以的速度沿方向匀速滑动,当滑块的右端与点B重合时,滑动停止.
2.滑块停顿.
3.滑块以小于的速度沿方向匀速返回,当滑块的左端与点A重合时,滑动停止.设滑动时间为时,滑块左端离点A的距离为,右端离点B的距离为,
(1)当时,求的值.
(2)整个滑动过程总用时(含停顿的时间),请根据所给条件解决下列问题:
①求滑块返回的速度.
②记,若,求t的值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】本题考查了解一元一次方程及一元一次方程的解,熟练掌握解一元一次方程的步骤是解题的关键.
【详解】解:A、的解是,故此选项不符合题意;
B、的解是,故此选项符合题意;
C、的解是,故此选项不符合题意;
D、的解是,故此选项不符合题意;
故选:B.
2.B
【分析】题目主要考查等式的性质,根据等式的性质逐一判断即可得答案,熟练掌握等式的基本性质是解题关键.
【详解】解:A、C、若,等式变形错误,故A、C不符合题意;
B、如果,那么,正确,故B符合题意;
D、如果,那么,故D不符合题意.
故选:B.
3.A
【分析】本题考查了一元一次方程的定义,以及一元一次方程的求解,一元一次方程指只含有一个未知数、未知数的最高次数为1且两边都为整式的等式.据此即可求解.
【详解】解:由题意得:,
∴
原方程为:,
解得:,
故选:A
4.D
【分析】本题考查一元一次方程的解,解题的关键是理清表格中数据的含义.方程整理为,根据表格确定出所求方程的解.
【详解】解:,
,
从表格中观察:当时,,
故选:D.
5.C
【分析】本题主要考查了一元一次方程的解和解法,先按照解一元一次方程的一般步骤,求出已知条件中两个方程的解,然后根据两个方程的解是互为相反数,列出关于的方程,解方程即可.解题关键是熟练掌握一元一次方程解的定义和解一元一次方程的一般步骤.
【详解】解: 由解得:,
,
方程两边同时乘得:,
去括号得:,
移项得:,
合并得:,
方程和方程 的解互为相反数,
,
,
,
故选:C.
6.C
【分析】本题主要考查了一元一次方程的解以及解一元一次方程,把代入,得出关于m的一元一次方程,解方程即可求解.
【详解】解:设常数项为m,则原方程为:,
把代入,
则方程变成:,
整理得:,
解得:,
故选:C.
7.B
【分析】本题主要考查了一元一次方程的应用,解题的关键是根据题意列出方程,准确计算.设中心数为x,根据5个数之和等于115,列出方程,解方程即可.
【详解】解:设中心数为x,根据题意得:
,
解得:,
∴此时十字方框正中心的数位于星期二这一列,
故选:B.
8.C
【分析】本题考查了一元一次方程的解的定义,熟记使一元一次方程左右两边相等的未知数的值叫做一元一次方程的解是解题的关键.
根据题中两个方程的关系,可知,即可求出y的值.
【详解】解:∵方程的解为,
∴方程的解满足,
解得:.
故选:C.
9.C
【分析】本题考查了一元一次方程的求解,分类讨论①若,即:时②若,即:时两种情况即可求解.
【详解】解:①若,即:时:
原方程为:,
解得:;
②若,即:时:
原方程为:,
解得:(舍去)
故选:C
10.D
【分析】观察图形可知,A型纸盒需要4个长方形纸板,1个正方形纸板,B型纸盒需要3个长方形纸板和2个正方形纸板,设A型盒子个数为x个,可得A型纸盒需要长方形纸板的数量和B型纸盒需要长方形纸板的数量,可列出方程对①进行判断;设B 型盒中正方形纸板的个数为m个,可得B型纸盒需要长方形纸板的数量和A型纸盒需要长方形纸板的数量,可列出方程对②进行判断;设制作A 型盒子a个,B型盒子b个,根据长方形纸板360张,正方形纸板120张,可得出方程组,解之即可得出a,b值,进而可对③④进行判断.
【详解】解:设A型盒子个数为x个,则A型盒子需要长方形纸板张,正方形纸板x张,
∵B型纸盒需要2个正方形纸板,
∴可制作B型纸盒的数量为个,需要长方形纸板张,
∴,故①正确;
设B 型盒中正方形纸板的个数为m个,则B型纸盒有个,需要长方形纸板张,A型盒子有个,
∴,故②正确;
设制作A 型盒子a个,B型盒子b个,
则,解得,
∴A型盒子有72个,B型纸盒有24个,
∴B型纸盒中正方形纸板48个,
故③④正确;
故正确的个数有4个.
故选:D.
【点睛】本题考查了由实际问题抽象出一元一次方程以及二元一次方程组的应用,找准等关系,正确列出一元一次方程(或二元一次方程组)是解题的关键.
11.
【分析】本题考查了列一元一次方程,根据题意直接列出一元一次方程即可求解,理解题意是解题的关键.
【详解】解:由题意可得,,
故答案为:.
12.2
【分析】此题主要考查了一元一次方程解的定义.解答此题的关键是熟知方程组有公共解的含义,考查了学生对题意的理解能力.
先求方程的解,再代入,求得的值.
【详解】解:解方程,得,
把代入,
得:,
解得.
故答案为:2.
13.
【分析】本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次方程是解题的关键.设绳索长x尺,则竿长尺,根据“将绳索对半折后再去量竿,就比竿短5尺”,即可得出关于x的一元一次方程,此题得解.
【详解】解:设绳索长x尺,则竿长尺,
依题意,得:,
故答案为:.
14.
【分析】本题考查解一元一次方程,解方程与方程,根据题中“友好方程”定义,列方程求解即可得到答案,熟练掌握一元一次方程解法是解决问题的关键.
【详解】解:解得;
解得;
关于的方程与方程是“友好方程”,
,解得,
故答案为:.
15.12
【分析】本题考查的是图形的变化规律,关键是通过图1中面积为10的阴影正方形,分析出图2中面积为5的阴影正方形,被全部覆盖的小方格有1个,被部分覆盖的小方格有8个;然后列式求解即可.
图1中阴影正方形的面积为10,被全部覆盖的小方格有4个,被部分覆盖的小方格有10个;则面积为5的阴影正方形,被全部覆盖的小方格有1个,被部分覆盖的小方格有8个;被全部覆盖的小方格数值即为m,被部分覆盖的小方格,数值分别为、、、、、、、;因,将式子进行化简计算即可.
【详解】解:如图所示,
面积为5的阴影正方形,被全部覆盖的小方格有1个,被部分覆盖的小方格有8个;
被全部覆盖的小方格数值即为m,被部分覆盖的小方格,数值分别为;
因为,即,
,
解得:.
故答案为:12.
16.(1)
(2)
【分析】本题考查一元一次方程的定义,方程的解.
(1)根据一元一次方程的定义可得,,求解即可;
(2)把代入方程,求解即可.
【详解】(1)∵关于x的方程是一元一次方程,
∴且
∴;
(2)由(1)得,该一元一次方程为,
∵是该方程的解,
∴,
∴.
17.(1)
(2)
【分析】本题主要考查解一元一次方程,去分母、去括号、移项、合并同类项、系数化为1,这仅是解一元一次方程的一般步骤,针对方程的特点,灵活应用,各种步骤都是为使方程逐渐向形式转化.
依次去括号、移项、合并同类项、系数化为1可得;
依次去括号、移项、合并同类项、系数化为1可得.
【详解】(1)解:
移项得:
合并同类项得:
系数化为1,得:
(2)解:
去括号得:
移项得:
合并同类项得:
系数化为1,得:
18.(1)
(2)x的值为或
【分析】此题考查了新定义运算,熟练掌握代数式的求值和解一元一次方程是解题的关键.
(1)根据题意代入求值即可;
(2)根据题意列出方程,解方程即可.
【详解】(1)解:当时,
.
(2)当时,即,
当时有:
,
;
当时有:
,
,
∴当时,x的值为或.
19.任务一:①等式的基本性质;乘法分配律;②三;移项时没有变号;③;任务二:①去分母时要给每一项乘以分母的最小公倍数数,特别是常数项是易错点;②去括号时,如果括号外是“” 号,括号内每一项都要变号;③移项时,注意移动项的符合的变化(不唯一).
【分析】本题主要考查了解一元一次方程,掌握解一元一次方程的基本步骤以及注意事项是解题的关键.
任务一:根据解一元一次方程的基本步骤逐步分析、判定即可解答;
任务二:结合解一元一次方程的经验,总结注意事项即可.
【详解】解:任务一:
①以上解题过程中,第一步的变形的依据是等式的基本性质;第二步去括号时依据的运算律是乘法分配律;
②以上解题过程中从第三步开始出现错误,这一步错误的原因是移项时没有变号;
由,
,
,
,
③该方程的正确解:;
故答案为:①等式的基本性质;乘法分配律;②三;移项时没有变号;③;
任务二:解一元一次方程需要注意以下事项:①去分母时要给每一项乘以分母的最小公倍数数,特别是常数项是易错点;②去括号时,如果括号外是“” 号,括号内每一项都要变号;③移项时,注意移动项的符合的变化
20.(1)小颖本局得分为6分
(2)小颖的说法不正确,理由见解析
【分析】本题主要考查有理数混合运算和一元一次方程的应用,
通过投中的区和各区的分数即可求得得分;
首先求得投中各区的次数,根据各区的分数列出本局得分代数式,再结合题意列出方程求解判断正确与否;
【详解】(1)解:∵A区4次,B区2次,脱靶4次,
∴(分).
则小颖本局得分为6分.
(2)由题意,得本局脱靶次数为:(次).
本局得分:(分).
∵小颖称本局得分比第一局高11分.
∴,解得,与题意不符.
所以,小颖的说法不正确.
21.(1)不是,理由见解析;
(2);
(3).
【分析】本题考查有理数的运算,一元一次方程的实际应用,代数式求值,理解“有趣数对”的定义,是解题的关键.
(1)根据“有趣数对”的定义,进行判断即可;
(2)根据“有趣数对”的定义,列出方程进行求解即可;
(3)先根据“有趣数对”的定义,得到,利用整体代入法求代数式的值即可.
【详解】(1)解:不是,理由如下,
∵,,,
∴数对不是“有趣数对”;
(2)∵是“有趣数对”,
∴
解得:;
(3)∵是“有趣数对”
∴,
即,
.
22.(1)A种服装的标价为300元
(2)①A种服装购进50件,B种服装购进60件;②剩余的B种服装打七折处理
【分析】本题考查了一元一次方程的应用;
(1)设A种服装的标价为元,根据利润率的计算方法列方程求解即可;
(2)①设购进的A种服装有件,则购进的B种服装有件,根据购进A,B两种服装共110件,所用资金为28000元列方程求解即可;
②设剩余的B种服装打折处理,根据只售的10件的金额加上处理部分的进而等于B种服装进货总额,列方程求解即可.
【详解】(1)解:设A种服装的标价为元,
由题意得:,
解得:,
答:A种服装的标价为300元;
(2)①设购进的A种服装有件,则购进的B种服装有件,
由题意得:,
解得:,
则,
答:A种服装购进50件,B种服装购进60件;
②设剩余的B种服装打折处理,
由题意得:,
解得:,
答:剩余的B种服装打七折处理.
23.(1)
(2)或
【分析】本题考查了一元一次方程的应用:
(1)根据时间等于路程除以速度,可知当时,滑块右端刚好与点B重合,即可求得答案;
(2)①先求得返回所用的时间,根据速度等于路程除以时间求解即可;②分两种情况讨论:1)当滑块从左向右滑动,2)当滑块从右向左滑动,根据题意列出方程求解即可.
【详解】(1)解:轨道长为,长度为的滑块从点A到点B的速度为,
第一阶段所用的时间为,
当时,滑块右端刚好与点B重合,;
(2)解:①整个过程用时,当滑块右端与点B重合时,滑块停顿,
第三阶段所用的时间为.
滑块返回的速度为.
②分析可得:,当时,显然第二阶段时不满足,所以分两种情况:
1)当滑块从左向右滑动,即时,,,,,解得;
2)当滑块从右向左滑动,即时,,,,解得.
综上所述,当或时,.
答案第1页,共2页
答案第1页,共2页
