第7章 数据的收集、整理、描述精选题练习(含解析)
文档属性
| 名称 | 第7章 数据的收集、整理、描述精选题练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 08:10:13 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学八年级下册苏科版第7章数据的收集、整理、描述精选题练习
一、单选题
1.下列调查中,适宜全面调查的是( )
A.调查春节联欢晚会的收视率
B.调查市场上某种食品的色素含量是否符合国家标准
C.调查某批次汽车的抗撞击能力
D.了解七年级(1)班同学每周体育锻炼的时间
2.为了解某市2022年中考数学学科各分数段成绩的分布情况,采用抽样调查方式从中随机抽取600名考生的中考数学成绩进行统计分析,在这一问题中,样本是指( )
A.600 B.被抽取的600名考生的中考数学成绩
C.被抽取的600名考生 D.某市2022年中考数学成绩
3.某校为了解七年级1200名新生的上学方式,随机对该年级部分学生的上学方式(乘车、步行、骑车)进行了调查,并根据调查结果绘制了条形统计图和扇形统计图,则下列判断错误的是( )
A.调查的学生中步行上学的有8名
B.扇形统计图中步行的学生人数所占的圆心角是
C.该校七年级学生中骑车上学的约有360名
D.扇形统计图中骑车的学生人数所占的圆心角是
4.下列实数,,,,中,无理数出现的频率为( )
A. B. C. D.
5.一组数据共40个数,分为5组,第1组到第3组的频数之和为27,第4组的频率是,则第5组的频数为( )
A.8 B.9 C.10 D.11
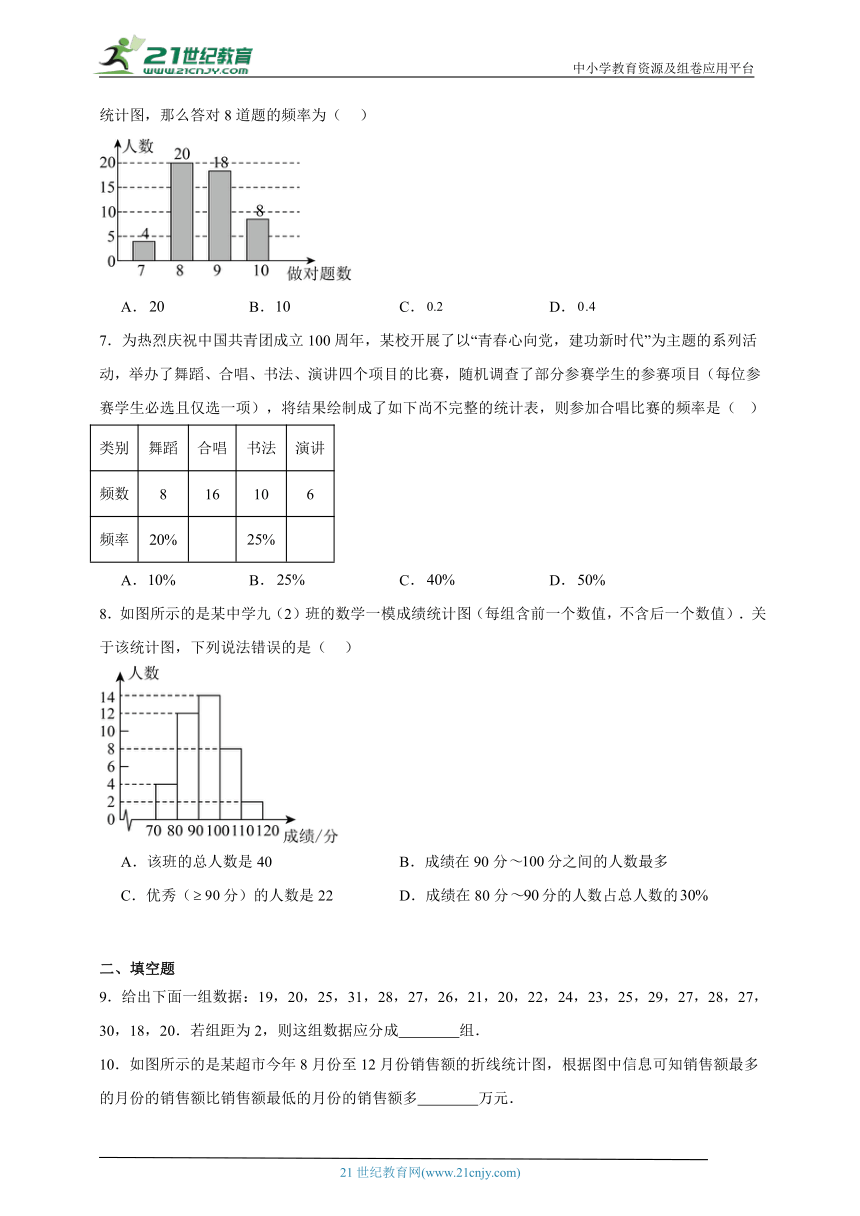
6.数学老师布置了道选择题作为课堂练习,榕榕将全班同学的答题情况绘制成了如图所示的条形统计图,那么答对8道题的频率为( )
A. B. C. D.
7.为热烈庆祝中国共青团成立100周年,某校开展了以“青春心向党,建功新时代”为主题的系列活动,举办了舞蹈、合唱、书法、演讲四个项目的比赛,随机调查了部分参赛学生的参赛项目(每位参赛学生必选且仅选一项),将结果绘制成了如下尚不完整的统计表,则参加合唱比赛的频率是( )
类别 舞蹈 合唱 书法 演讲
频数 8 16 10 6
频率
A. B. C. D.
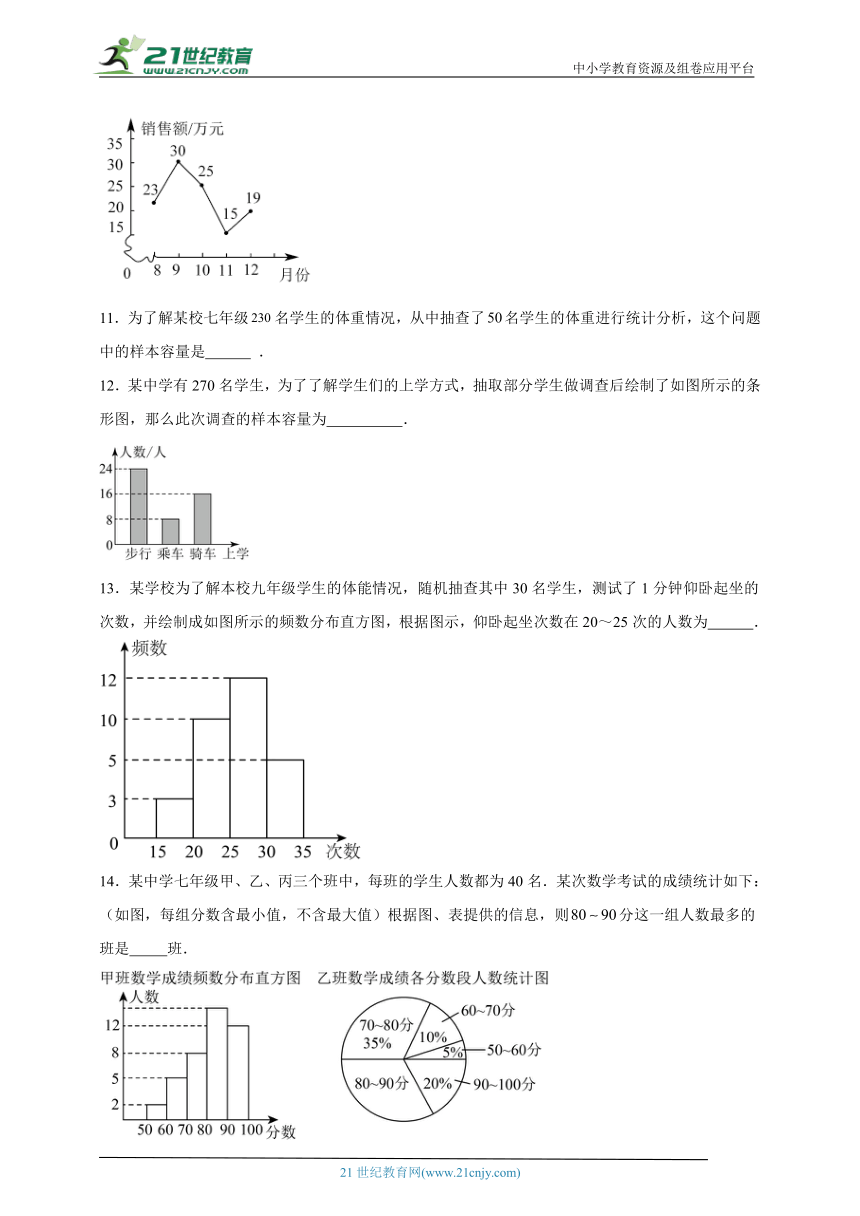
8.如图所示的是某中学九(2)班的数学一模成绩统计图(每组含前一个数值,不含后一个数值).关于该统计图,下列说法错误的是( )
A.该班的总人数是40 B.成绩在90分分之间的人数最多
C.优秀(分)的人数是22 D.成绩在80分分的人数占总人数的
二、填空题
9.给出下面一组数据:19,20,25,31,28,27,26,21,20,22,24,23,25,29,27,28,27,30,18,20.若组距为2,则这组数据应分成 组.
10.如图所示的是某超市今年8月份至12月份销售额的折线统计图,根据图中信息可知销售额最多的月份的销售额比销售额最低的月份的销售额多 万元.
11.为了解某校七年级名学生的体重情况,从中抽查了名学生的体重进行统计分析,这个问题中的样本容量是 .
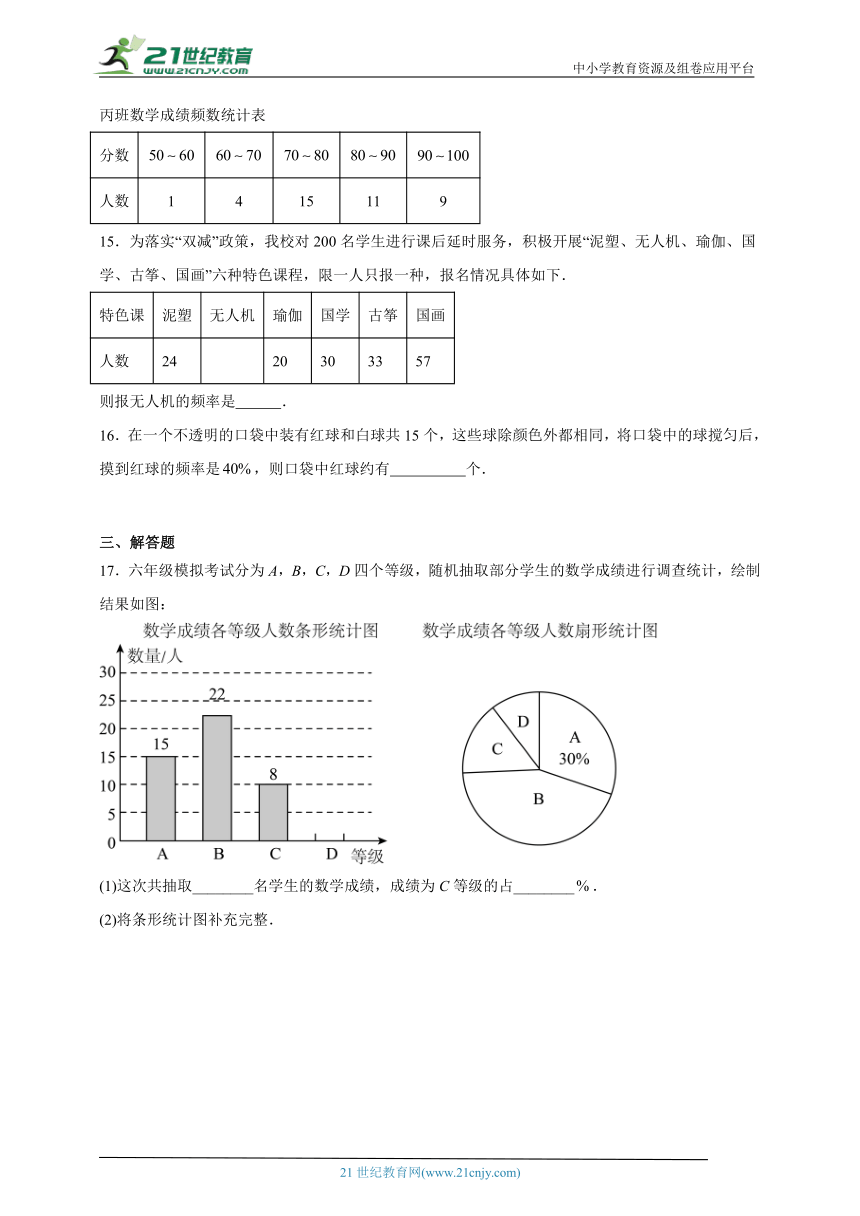
12.某中学有270名学生,为了了解学生们的上学方式,抽取部分学生做调查后绘制了如图所示的条形图,那么此次调查的样本容量为 .
13.某学校为了解本校九年级学生的体能情况,随机抽查其中30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,根据图示,仰卧起坐次数在20~25次的人数为 .
14.某中学七年级甲、乙、丙三个班中,每班的学生人数都为40名.某次数学考试的成绩统计如下:(如图,每组分数含最小值,不含最大值)根据图、表提供的信息,则分这一组人数最多的班是 班.
丙班数学成绩频数统计表
分数
人数 1 4 15 11 9
15.为落实“双减”政策,我校对200名学生进行课后延时服务,积极开展“泥塑、无人机、瑜伽、国学、古筝、国画”六种特色课程,限一人只报一种,报名情况具体如下.
特色课 泥塑 无人机 瑜伽 国学 古筝 国画
人数 24 20 30 33 57
则报无人机的频率是 .
16.在一个不透明的口袋中装有红球和白球共15个,这些球除颜色外都相同,将口袋中的球搅匀后,摸到红球的频率是,则口袋中红球约有 个.
三、解答题
17.六年级模拟考试分为A,B,C,D四个等级,随机抽取部分学生的数学成绩进行调查统计,绘制结果如图:
(1)这次共抽取________名学生的数学成绩,成绩为C等级的占________.
(2)将条形统计图补充完整.
18.某中学六年级共有学生171人,其中1班有48人.为了迎接新年,全年级师生组织了一场迎新演出,各班同学踊跃参加,如图是各班参演学生人数情况统计图.请根据图中提供的信息解答下列问题:
(1)表示“2班参演学生人数”的扇形的圆心角度数是______.
(2)如果3班的参演学生人数比4班的少9人,求全年级的参演学生人数.
(3)如果1班和2班的参演学生人数之和是这两个班级学生总人数的,3班和4班的参演学生人数之和是这两个班级学生总人数的,求2班的学生总人数.
19.某校体育老师为了研究八年级学生赛跑后心率的分布情况,随机抽取了该年级名学生,测量了他们赛跑后的脉搏次数,结果如下:
脉搏次数(次/分) 频数/学生人数
▲
▲
(1)该调查中的个体是▲;
(2)该老师将上述数据分组后,列出了右边的频数分布表,请将频数分布表补充完整;
(3)根据频数分布表画出频数分布直方图.
20.某公司在过去几年内使用某种型号的节能灯1000支,该公司对这些灯管的使用寿命(单位:小时)进行了统计,统计结果如下表所示:
分组 1700以上
频数 48 121 208 223 193 207
频率
(1)将各组的频率填入表中;
(2)根据上述统计结果,计算灯管使用寿命不足1500小时的频率.
21.为监测的情况,随机抽取达州市天的空气质量状况,统计如下:
污染指数()
天数()
其中时,空气质量为优;时,空气质量为良;时,空气质量为轻微污染.
(1)该市这天中有多少天空气质量达到优良?
(2)该市这天中,空气质量为轻微污染的天数的频率是多少?(结果精确到百分位)
22.郑州市气象台2023年12月11日3时40分发布暴雪红色预警信号:过去6小时,郑州站降雪量已达毫米,积雪深度厘米.当天,郑州市教育局下发了关于极端恶劣天气条件下临时停课的通知.某校学生积极参加社区组织的扫雪除冰工作,小明同学为了解七、八年级学生的参与时间(分钟),从两个年级各随机抽取名学生进行调查,并对数据(时间)进行整理、表示和分析.
①八年级学生参与时间的频数直方图如图(数据分成组:,,,,,).
②八年级学生参与时间在这一组的是:,,,,,,,,,,,,,.
③学生参与时间的平均数、中位数、众数如下表.
年级 平均数 中位数 众数
七年级
八年级
根据以上信息,回答下列问题:
(1)表格中______.
(2)你认为哪个年级学生参与扫雪除冰工作更积极?请说明理由.
(3)七年级共有学生名,七(4)班学生小亮说:“我参与扫雪除冰分钟,高于七年级学生扫雪除冰时间的平均数分钟,所以七年级至少有名学生比我参与的时间少.”小亮的说法是否正确?请说明理由.
参考答案:
1.D
【分析】本题考查对调查方式的选择,根据普查结果准确,所以在要求精确、难度相对不大,实验无破坏性的情况下应选择普查方式,当考查的对象很多或考查会给被调查对象带来损伤破坏,以及考查经费和时间都非常有限时,普查就受到限制,这时就应选择抽样调查.
【详解】解:A、调查春节联欢晚会的收视率,适宜抽样调查,不符合题意.
B、调查市场上某种食品的色素含量是否符合国家标准,适宜抽样调查,不符合题意.
C、调查某批次汽车的抗撞击能力,适宜抽样调查,不符合题意.
D、了解七年级(1)班同学每周体育锻炼的时间,适宜全面调查,符合题意.
故选:D.
2.B
【分析】本题考查总体、个体、样本、样本容量,根据样本的定义,结合具体的问题情境进行解答即可,理解样本的意义是正确解答的关键.
【详解】在这个问题中,样本是被抽取的600名考生的中考数学成绩.
故选:B.
3.D
【分析】本题考查利用条形统计图和扇形统计图综合判断,能从统计图中提取相关信息进行计算是解题的关键.
【详解】解:A. 调查的学生中步行上学的有名,正确;
B. 扇形统计图中步行的学生人数所占的圆心角是,正确;
C. 该校七年级学生中骑车上学的约有名,正确
D. 扇形统计图中骑车的学生人数所占的圆心角是,错误;
故选D.
4.C
【分析】本题考查频数与频率,算术平方根,无理数,解题的关键是根据无理数的定义以及“频率=频数÷总数”进行列式计算即可.
【详解】解:下列实数,,,,中,无理数有:,,,共个,
∴无理数出现的频率为:.
故选:C.
5.B
【分析】本题考查了频数与频率,根据频数=总次数×频率先求出第四组的频数,然后再进行计算即可解答.
【详解】解:由题意得:第4组的频数,
∵第1组到第3组的频数之和为27,
∴第5组的频数,
故选:B.
6.D
【分析】本题考查了频率的计算方法,频数与数据总数的比值为频率,频率反映了各组频数的大小在总数中所占的分量.
根据题目中所给的条形统计图,求出全班学生的总人数,利用答对8道题的学生人数除以全班总人数即可得答对8道题的同学的频率.
【详解】解:由条形统计图可得,全班学生人数为:(人),
答对8道题的学生人数为人,
∴答对8道题的同学的频率为:.
故选:D.
7.C
【分析】本题考查频数分布表,先根据表中数据求得调查总人数,进而求参加合唱频率即可.
【详解】解:由表可知,调查总人数为(人),
∴参加合唱比赛的频率为,
故选:C.
8.C
【分析】本题主要考查了频数分布直方图,从直方图上获得所需信息是解题的关键.
根据从直方图上获取的信息逐项判断即可解答.
【详解】解:A.该班的总人数是,故A选项说法正确,但不符合题意;
B.由统计图可知,成绩在90分分之间的人数是14,是最多的,故B选项说法正确,但不符合题意;
C.优秀(分)的人数是,故C选项说法错误,符合题意;
D.成绩在80分的人数是12,占总人数的,故D选项说法正确,但不符合题意.
故选:C.
9.7
【分析】本题考查组距、组数之间的关系等知识,掌握组数的定义是本题的关键,即数据分成的组的个数称为组数.用极差除以组距,如果商是整数,组数=这个整数加1,如果商不是整数,用进一法,确定组数.
【详解】解:∵,,
∴分成的组数7组,
故答案为:7.
10.15
【分析】本题考查了从统计图分析数据等知识,根据折线统计图得到销售额最多的月份为9月,销售额为30万元,销售额最少的月份为11月,销售额为15万元,相减即可求解.
【详解】解:由统计图得销售额最多的月份为9月,销售额为30万元,销售额最少的月份为11月,销售额为15万元,
(万元).
故答案为:15
11.
【分析】本题考查了总体、个体、样本、样本容量,根据总体、个体、样本、样本容量的意义,即可解答.
【详解】解:为了解某校七年级名学生的体重情况,从中抽查了名学生的体重进行统计分析,这个问题中的样本容量是,
故答案为:50
12.
【分析】本题主要考查了求样本容量,根据样本容量的定义进行求解即可:一个样本包括的个体数量叫做样本容量可得答案.熟知相关定义是解题的关键,样本容量是指样本中包含个体的数目,没有单位.
【详解】解:由题意得,样本容量为,
故答案为:.
13.10
【分析】本题考查读频数分布直方图的能力,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
【详解】解:读图可知:仰卧起坐次数在20~25次的人数是10,
故答案为:10.
14.甲
【分析】本题考查频数分布直方图、扇形统计图、频数分布表,解答本题的关键是明确题意,利用数形结合的思想解答.
根据题意和统计图表中的信息,可以得到甲、乙、丙三个班中分这一组人数,然后比较大小,即可解答本题.
【详解】解:甲班分这一组有(人),
乙班分这一组有(人),
丙班分这一组有11人,
∵,
∴分这一组人数最多的是甲班,
故答案为:甲.
15.
【分析】本题主要考查了求频率,先求出报名无人机的人数,再用报名无人机的人数除以总人数即可得到答案.
【详解】解:由题意得,报名无人机的人数为人,
∴报无人机的频率是,
故答案为:.
16.6
【分析】本题考查了利用频率估计概率:大量重复试验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.用频率估计概率得到的是近似值,随试验次数的增多,值越来越精确.已知摸到红球的频率是,根据概率公式计算这个口袋中红球的数量.
【详解】解:因为摸到红球的频率是,
所以估计这个口袋中红球的数量为(个).
故答案为:6.
17.(1)50,
(2)见解析
【分析】本题主要考查统计图表:
(1)用A等人数除以所占总人数的百分数即可,用成绩为C等级的学生数除以总人数即可求出C等级的学生数占总人数的百分数;
(2)用总人数减去A、B、C等级的人数,即可求出D等级的人数,然后画图即可
【详解】(1)解:(名);
,
故答案为:50;16;
(2)解:(名)
画图如下:
18.(1)
(2)全年级的参演学生人数为72人
(3)2班的学生总人数为42人
【分析】本题考查扇形统计图,一元一次方程的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
(1)根据扇形统计图中的数据,可以计算出“2班参演学生人数”的扇形的圆心角度数;
(2)根据3班的参演学生人数比4班的少9人,列式计算即可;
(3)根据题意列式计算即可.
【详解】(1)解: ,
答:表示“2班参演学生人数”的扇形的圆心角度数是,
(2)解:(人,
答:全年级的参演学生人数为72人;
(3)解:设2班的学生总人数为人,
根据题意得,,
解得,
答:2班的学生总人数为42人.
19.(1)每一名学生赛跑后的脉搏次数
(2)142,142,2,5
(3)见解析
【分析】本题考查频数分布表、频率分布直方图,整体、个体,理解整体、个体的意义;
(1)根据总体、个体的意义结合实际问题情境得出答案;
(2)求出表格中的分组,依据组距和频数统计可得答案;
(3)根据频数分布表画出频数分布直方图.
【详解】(1)该年级每名学生赛跑后1的脉搏次数;
故答案为该年级每名学生赛跑后1min的脉搏次数;
(2)根据组距为5,可得各组的分界值,根据频数统计可得各组频数,
脉搏次数(次/分) 频数/学生人数
故答案为:,,,;
(3)频率分布直方图如图所示.
20.(1)见解析
(2)
【分析】(1)由频率,可得出各组的频率;
(2)要计算灯管使用寿命不足1500小时的频率,即计算前四个小组的频率之和.
【详解】(1)解: ,,,,,;
填表如下:
分组 1700以上
频数 48 121 208 223 193 207
频率
(2)由(1)可得,
所以灯管使用寿命不足1500小时的频率为.
【点睛】本题主要考查了频率分布表的计算和频数分布直方图的应用以及概率的求法,属于基础题.
21.(1)天
(2)
【分析】(1)从表中找出空气质量达到优良的天数,然后求出它们的和即可;
(2)从表中找出空气质量为轻微污染的天数,然后求比即可.
【详解】(1)解:时,空气质量为优,时,空气质量为良,
天中空气质量达到优良的天数为:(天);
(2)天中,空气质量为轻微污染的天数是(天),
天中,空气质量为轻微污染的天数的频率是.
【点睛】本题考查频率的定义,读懂统计表,从统计表中获取信息是解题关键.
22.(1)
(2)八年级学生参与扫雪除冰工作更积极,理由见解析
(3)小亮的说法错误,理由见解析
【分析】本题考查了频数分布直方图、众数、中位数以及加权平均数,能够从图表中获取必要信息是解题的关键.
(1)根据中位数的定义解答即可;
(2)根据平均数和中位数的定义即可解答;
(3)根据中位数的意义解答即可.
【详解】(1)解:把年级名学生参与扫雪除冰的时间从小到大排列,排在中间的两位数分别是,,
中位数,
故答案为:;
(2)八年级学生参与扫雪除冰工作更积极,理由如下:
八年级参与扫雪除冰工作时间的平均数和中位数均大于七年级,所以八年级学生参与扫雪除冰工作更积极;
(3)小亮的说法错误,理由如下:
小亮参与扫雪除冰分钟,低于七年级的中位数,所以七年级至少有名学生比小亮参与的时间多.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学八年级下册苏科版第7章数据的收集、整理、描述精选题练习
一、单选题
1.下列调查中,适宜全面调查的是( )
A.调查春节联欢晚会的收视率
B.调查市场上某种食品的色素含量是否符合国家标准
C.调查某批次汽车的抗撞击能力
D.了解七年级(1)班同学每周体育锻炼的时间
2.为了解某市2022年中考数学学科各分数段成绩的分布情况,采用抽样调查方式从中随机抽取600名考生的中考数学成绩进行统计分析,在这一问题中,样本是指( )
A.600 B.被抽取的600名考生的中考数学成绩
C.被抽取的600名考生 D.某市2022年中考数学成绩
3.某校为了解七年级1200名新生的上学方式,随机对该年级部分学生的上学方式(乘车、步行、骑车)进行了调查,并根据调查结果绘制了条形统计图和扇形统计图,则下列判断错误的是( )
A.调查的学生中步行上学的有8名
B.扇形统计图中步行的学生人数所占的圆心角是
C.该校七年级学生中骑车上学的约有360名
D.扇形统计图中骑车的学生人数所占的圆心角是
4.下列实数,,,,中,无理数出现的频率为( )
A. B. C. D.
5.一组数据共40个数,分为5组,第1组到第3组的频数之和为27,第4组的频率是,则第5组的频数为( )
A.8 B.9 C.10 D.11
6.数学老师布置了道选择题作为课堂练习,榕榕将全班同学的答题情况绘制成了如图所示的条形统计图,那么答对8道题的频率为( )
A. B. C. D.
7.为热烈庆祝中国共青团成立100周年,某校开展了以“青春心向党,建功新时代”为主题的系列活动,举办了舞蹈、合唱、书法、演讲四个项目的比赛,随机调查了部分参赛学生的参赛项目(每位参赛学生必选且仅选一项),将结果绘制成了如下尚不完整的统计表,则参加合唱比赛的频率是( )
类别 舞蹈 合唱 书法 演讲
频数 8 16 10 6
频率
A. B. C. D.
8.如图所示的是某中学九(2)班的数学一模成绩统计图(每组含前一个数值,不含后一个数值).关于该统计图,下列说法错误的是( )
A.该班的总人数是40 B.成绩在90分分之间的人数最多
C.优秀(分)的人数是22 D.成绩在80分分的人数占总人数的
二、填空题
9.给出下面一组数据:19,20,25,31,28,27,26,21,20,22,24,23,25,29,27,28,27,30,18,20.若组距为2,则这组数据应分成 组.
10.如图所示的是某超市今年8月份至12月份销售额的折线统计图,根据图中信息可知销售额最多的月份的销售额比销售额最低的月份的销售额多 万元.
11.为了解某校七年级名学生的体重情况,从中抽查了名学生的体重进行统计分析,这个问题中的样本容量是 .
12.某中学有270名学生,为了了解学生们的上学方式,抽取部分学生做调查后绘制了如图所示的条形图,那么此次调查的样本容量为 .
13.某学校为了解本校九年级学生的体能情况,随机抽查其中30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,根据图示,仰卧起坐次数在20~25次的人数为 .
14.某中学七年级甲、乙、丙三个班中,每班的学生人数都为40名.某次数学考试的成绩统计如下:(如图,每组分数含最小值,不含最大值)根据图、表提供的信息,则分这一组人数最多的班是 班.
丙班数学成绩频数统计表
分数
人数 1 4 15 11 9
15.为落实“双减”政策,我校对200名学生进行课后延时服务,积极开展“泥塑、无人机、瑜伽、国学、古筝、国画”六种特色课程,限一人只报一种,报名情况具体如下.
特色课 泥塑 无人机 瑜伽 国学 古筝 国画
人数 24 20 30 33 57
则报无人机的频率是 .
16.在一个不透明的口袋中装有红球和白球共15个,这些球除颜色外都相同,将口袋中的球搅匀后,摸到红球的频率是,则口袋中红球约有 个.
三、解答题
17.六年级模拟考试分为A,B,C,D四个等级,随机抽取部分学生的数学成绩进行调查统计,绘制结果如图:
(1)这次共抽取________名学生的数学成绩,成绩为C等级的占________.
(2)将条形统计图补充完整.
18.某中学六年级共有学生171人,其中1班有48人.为了迎接新年,全年级师生组织了一场迎新演出,各班同学踊跃参加,如图是各班参演学生人数情况统计图.请根据图中提供的信息解答下列问题:
(1)表示“2班参演学生人数”的扇形的圆心角度数是______.
(2)如果3班的参演学生人数比4班的少9人,求全年级的参演学生人数.
(3)如果1班和2班的参演学生人数之和是这两个班级学生总人数的,3班和4班的参演学生人数之和是这两个班级学生总人数的,求2班的学生总人数.
19.某校体育老师为了研究八年级学生赛跑后心率的分布情况,随机抽取了该年级名学生,测量了他们赛跑后的脉搏次数,结果如下:
脉搏次数(次/分) 频数/学生人数
▲
▲
(1)该调查中的个体是▲;
(2)该老师将上述数据分组后,列出了右边的频数分布表,请将频数分布表补充完整;
(3)根据频数分布表画出频数分布直方图.
20.某公司在过去几年内使用某种型号的节能灯1000支,该公司对这些灯管的使用寿命(单位:小时)进行了统计,统计结果如下表所示:
分组 1700以上
频数 48 121 208 223 193 207
频率
(1)将各组的频率填入表中;
(2)根据上述统计结果,计算灯管使用寿命不足1500小时的频率.
21.为监测的情况,随机抽取达州市天的空气质量状况,统计如下:
污染指数()
天数()
其中时,空气质量为优;时,空气质量为良;时,空气质量为轻微污染.
(1)该市这天中有多少天空气质量达到优良?
(2)该市这天中,空气质量为轻微污染的天数的频率是多少?(结果精确到百分位)
22.郑州市气象台2023年12月11日3时40分发布暴雪红色预警信号:过去6小时,郑州站降雪量已达毫米,积雪深度厘米.当天,郑州市教育局下发了关于极端恶劣天气条件下临时停课的通知.某校学生积极参加社区组织的扫雪除冰工作,小明同学为了解七、八年级学生的参与时间(分钟),从两个年级各随机抽取名学生进行调查,并对数据(时间)进行整理、表示和分析.
①八年级学生参与时间的频数直方图如图(数据分成组:,,,,,).
②八年级学生参与时间在这一组的是:,,,,,,,,,,,,,.
③学生参与时间的平均数、中位数、众数如下表.
年级 平均数 中位数 众数
七年级
八年级
根据以上信息,回答下列问题:
(1)表格中______.
(2)你认为哪个年级学生参与扫雪除冰工作更积极?请说明理由.
(3)七年级共有学生名,七(4)班学生小亮说:“我参与扫雪除冰分钟,高于七年级学生扫雪除冰时间的平均数分钟,所以七年级至少有名学生比我参与的时间少.”小亮的说法是否正确?请说明理由.
参考答案:
1.D
【分析】本题考查对调查方式的选择,根据普查结果准确,所以在要求精确、难度相对不大,实验无破坏性的情况下应选择普查方式,当考查的对象很多或考查会给被调查对象带来损伤破坏,以及考查经费和时间都非常有限时,普查就受到限制,这时就应选择抽样调查.
【详解】解:A、调查春节联欢晚会的收视率,适宜抽样调查,不符合题意.
B、调查市场上某种食品的色素含量是否符合国家标准,适宜抽样调查,不符合题意.
C、调查某批次汽车的抗撞击能力,适宜抽样调查,不符合题意.
D、了解七年级(1)班同学每周体育锻炼的时间,适宜全面调查,符合题意.
故选:D.
2.B
【分析】本题考查总体、个体、样本、样本容量,根据样本的定义,结合具体的问题情境进行解答即可,理解样本的意义是正确解答的关键.
【详解】在这个问题中,样本是被抽取的600名考生的中考数学成绩.
故选:B.
3.D
【分析】本题考查利用条形统计图和扇形统计图综合判断,能从统计图中提取相关信息进行计算是解题的关键.
【详解】解:A. 调查的学生中步行上学的有名,正确;
B. 扇形统计图中步行的学生人数所占的圆心角是,正确;
C. 该校七年级学生中骑车上学的约有名,正确
D. 扇形统计图中骑车的学生人数所占的圆心角是,错误;
故选D.
4.C
【分析】本题考查频数与频率,算术平方根,无理数,解题的关键是根据无理数的定义以及“频率=频数÷总数”进行列式计算即可.
【详解】解:下列实数,,,,中,无理数有:,,,共个,
∴无理数出现的频率为:.
故选:C.
5.B
【分析】本题考查了频数与频率,根据频数=总次数×频率先求出第四组的频数,然后再进行计算即可解答.
【详解】解:由题意得:第4组的频数,
∵第1组到第3组的频数之和为27,
∴第5组的频数,
故选:B.
6.D
【分析】本题考查了频率的计算方法,频数与数据总数的比值为频率,频率反映了各组频数的大小在总数中所占的分量.
根据题目中所给的条形统计图,求出全班学生的总人数,利用答对8道题的学生人数除以全班总人数即可得答对8道题的同学的频率.
【详解】解:由条形统计图可得,全班学生人数为:(人),
答对8道题的学生人数为人,
∴答对8道题的同学的频率为:.
故选:D.
7.C
【分析】本题考查频数分布表,先根据表中数据求得调查总人数,进而求参加合唱频率即可.
【详解】解:由表可知,调查总人数为(人),
∴参加合唱比赛的频率为,
故选:C.
8.C
【分析】本题主要考查了频数分布直方图,从直方图上获得所需信息是解题的关键.
根据从直方图上获取的信息逐项判断即可解答.
【详解】解:A.该班的总人数是,故A选项说法正确,但不符合题意;
B.由统计图可知,成绩在90分分之间的人数是14,是最多的,故B选项说法正确,但不符合题意;
C.优秀(分)的人数是,故C选项说法错误,符合题意;
D.成绩在80分的人数是12,占总人数的,故D选项说法正确,但不符合题意.
故选:C.
9.7
【分析】本题考查组距、组数之间的关系等知识,掌握组数的定义是本题的关键,即数据分成的组的个数称为组数.用极差除以组距,如果商是整数,组数=这个整数加1,如果商不是整数,用进一法,确定组数.
【详解】解:∵,,
∴分成的组数7组,
故答案为:7.
10.15
【分析】本题考查了从统计图分析数据等知识,根据折线统计图得到销售额最多的月份为9月,销售额为30万元,销售额最少的月份为11月,销售额为15万元,相减即可求解.
【详解】解:由统计图得销售额最多的月份为9月,销售额为30万元,销售额最少的月份为11月,销售额为15万元,
(万元).
故答案为:15
11.
【分析】本题考查了总体、个体、样本、样本容量,根据总体、个体、样本、样本容量的意义,即可解答.
【详解】解:为了解某校七年级名学生的体重情况,从中抽查了名学生的体重进行统计分析,这个问题中的样本容量是,
故答案为:50
12.
【分析】本题主要考查了求样本容量,根据样本容量的定义进行求解即可:一个样本包括的个体数量叫做样本容量可得答案.熟知相关定义是解题的关键,样本容量是指样本中包含个体的数目,没有单位.
【详解】解:由题意得,样本容量为,
故答案为:.
13.10
【分析】本题考查读频数分布直方图的能力,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
【详解】解:读图可知:仰卧起坐次数在20~25次的人数是10,
故答案为:10.
14.甲
【分析】本题考查频数分布直方图、扇形统计图、频数分布表,解答本题的关键是明确题意,利用数形结合的思想解答.
根据题意和统计图表中的信息,可以得到甲、乙、丙三个班中分这一组人数,然后比较大小,即可解答本题.
【详解】解:甲班分这一组有(人),
乙班分这一组有(人),
丙班分这一组有11人,
∵,
∴分这一组人数最多的是甲班,
故答案为:甲.
15.
【分析】本题主要考查了求频率,先求出报名无人机的人数,再用报名无人机的人数除以总人数即可得到答案.
【详解】解:由题意得,报名无人机的人数为人,
∴报无人机的频率是,
故答案为:.
16.6
【分析】本题考查了利用频率估计概率:大量重复试验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.用频率估计概率得到的是近似值,随试验次数的增多,值越来越精确.已知摸到红球的频率是,根据概率公式计算这个口袋中红球的数量.
【详解】解:因为摸到红球的频率是,
所以估计这个口袋中红球的数量为(个).
故答案为:6.
17.(1)50,
(2)见解析
【分析】本题主要考查统计图表:
(1)用A等人数除以所占总人数的百分数即可,用成绩为C等级的学生数除以总人数即可求出C等级的学生数占总人数的百分数;
(2)用总人数减去A、B、C等级的人数,即可求出D等级的人数,然后画图即可
【详解】(1)解:(名);
,
故答案为:50;16;
(2)解:(名)
画图如下:
18.(1)
(2)全年级的参演学生人数为72人
(3)2班的学生总人数为42人
【分析】本题考查扇形统计图,一元一次方程的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
(1)根据扇形统计图中的数据,可以计算出“2班参演学生人数”的扇形的圆心角度数;
(2)根据3班的参演学生人数比4班的少9人,列式计算即可;
(3)根据题意列式计算即可.
【详解】(1)解: ,
答:表示“2班参演学生人数”的扇形的圆心角度数是,
(2)解:(人,
答:全年级的参演学生人数为72人;
(3)解:设2班的学生总人数为人,
根据题意得,,
解得,
答:2班的学生总人数为42人.
19.(1)每一名学生赛跑后的脉搏次数
(2)142,142,2,5
(3)见解析
【分析】本题考查频数分布表、频率分布直方图,整体、个体,理解整体、个体的意义;
(1)根据总体、个体的意义结合实际问题情境得出答案;
(2)求出表格中的分组,依据组距和频数统计可得答案;
(3)根据频数分布表画出频数分布直方图.
【详解】(1)该年级每名学生赛跑后1的脉搏次数;
故答案为该年级每名学生赛跑后1min的脉搏次数;
(2)根据组距为5,可得各组的分界值,根据频数统计可得各组频数,
脉搏次数(次/分) 频数/学生人数
故答案为:,,,;
(3)频率分布直方图如图所示.
20.(1)见解析
(2)
【分析】(1)由频率,可得出各组的频率;
(2)要计算灯管使用寿命不足1500小时的频率,即计算前四个小组的频率之和.
【详解】(1)解: ,,,,,;
填表如下:
分组 1700以上
频数 48 121 208 223 193 207
频率
(2)由(1)可得,
所以灯管使用寿命不足1500小时的频率为.
【点睛】本题主要考查了频率分布表的计算和频数分布直方图的应用以及概率的求法,属于基础题.
21.(1)天
(2)
【分析】(1)从表中找出空气质量达到优良的天数,然后求出它们的和即可;
(2)从表中找出空气质量为轻微污染的天数,然后求比即可.
【详解】(1)解:时,空气质量为优,时,空气质量为良,
天中空气质量达到优良的天数为:(天);
(2)天中,空气质量为轻微污染的天数是(天),
天中,空气质量为轻微污染的天数的频率是.
【点睛】本题考查频率的定义,读懂统计表,从统计表中获取信息是解题关键.
22.(1)
(2)八年级学生参与扫雪除冰工作更积极,理由见解析
(3)小亮的说法错误,理由见解析
【分析】本题考查了频数分布直方图、众数、中位数以及加权平均数,能够从图表中获取必要信息是解题的关键.
(1)根据中位数的定义解答即可;
(2)根据平均数和中位数的定义即可解答;
(3)根据中位数的意义解答即可.
【详解】(1)解:把年级名学生参与扫雪除冰的时间从小到大排列,排在中间的两位数分别是,,
中位数,
故答案为:;
(2)八年级学生参与扫雪除冰工作更积极,理由如下:
八年级参与扫雪除冰工作时间的平均数和中位数均大于七年级,所以八年级学生参与扫雪除冰工作更积极;
(3)小亮的说法错误,理由如下:
小亮参与扫雪除冰分钟,低于七年级的中位数,所以七年级至少有名学生比小亮参与的时间多.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
