第5章 二次函数重难点检测卷(含解析)
文档属性
| 名称 | 第5章 二次函数重难点检测卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 740.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 08:36:17 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学苏科版九年级下册第5章二次函数重难点检测卷
一、选择题
1.关于二次函数,下列说法正确的是( )
A.函数图象的开口向下 B.函数图象的顶点坐标是
C.该函数的最大值是5 D.当时,y随x的增大而增大
2.如图,二次函数的图象与x轴交于,B两点,下列说法正确的是( )
A.抛物线的对称轴为直线
B.抛物线的顶点坐标为
C.A,B两点之间的距离为5
D.当时,y的值随x值的增大而增大
3.若点、都在二次函数的图象上,则a与b的大小关系( )
A. B. C. D.无法确定
4. 二次函数y=ax2+3x﹣1与x轴的交点个数是( )
A.2 B.1 C.0 D.不能确定
5.二次函数 的图象与x轴有交点,则k的取值范围是( )
A. B. 且
C. D. 且
6.如图,一名学生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是y=(x-10)(x+4),则铅球推出的距离OA=( )
A.14m B.10m C.7m D.4m
7.二次函数y=ax2+bx+1的图象与一次函数y=2ax+b在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
8.若一次函数y=(n+1)x+n的图象过第一、三、四象限,则函数y=nx2﹣nx( )
A.有最大值 B.有最大值
C.有最小值 D.有最小值
9.已知 和 均是以 为自变量的函数,当 时,函数值分别是 和 ,若存在实数 ,使得 ,则称函数 和 具有性质P。以下函数 和 具有性质P的是( )
A. 和 B. 和
C. 和 D. 和
10.如图,已知开口向上的抛物线与轴交于点,对称轴为直线.下列结论:①;②;③若关于的方程一定有两个不相等的实数根;④.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.把抛物线y=x2+1向右平移1个单位,所得新抛物线的表达式是 .
12. 关于的二次函数,在时有最大值6,则 .
13.如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米.水面下降1米时,水面的宽度为 米.
14.如图,王叔叔想用长为的栅栏,再借助房屋的外墙围成一个矩形羊圈,已知房屋外墙足够长,当矩形的边 时,羊圈的面积最大.
15.已知点是抛物线上一动点.
(1)当点M到y轴的距离不大于1时,b的取值范围是 ;
(2)当点M到直线的距离不大于时,b的取值范围是,则的值为 .
16.某广场要建一个圆形喷水池,计划在池中心位置竖直安装一根带有喷水头的水管,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m(如图).若水柱落地处离池中心的水平距离也为3m,则水管的设计高度应为 m.
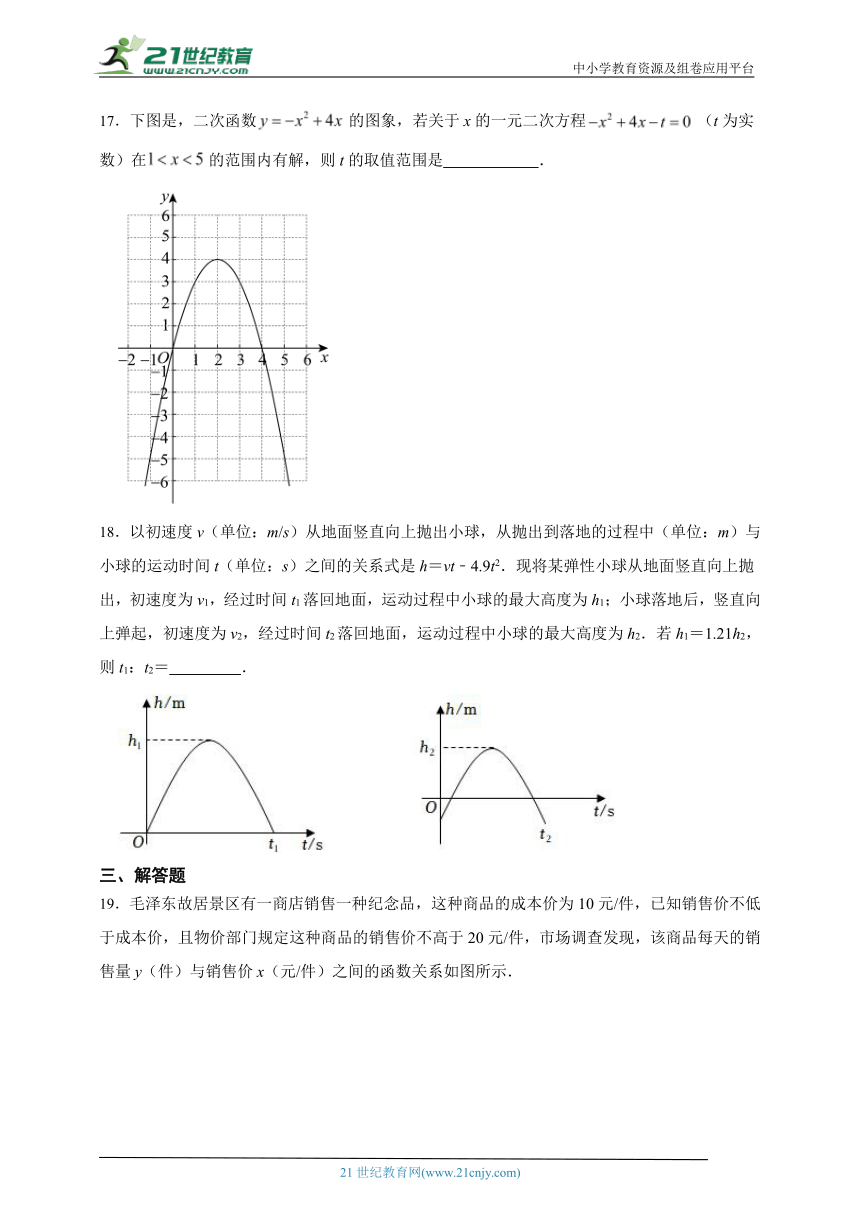
17.下图是,二次函数的图象,若关于x的一元二次方程(t为实数)在的范围内有解,则t的取值范围是 .
18.以初速度v(单位:m/s)从地面竖直向上抛出小球,从抛出到落地的过程中(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=vt﹣4.9t2.现将某弹性小球从地面竖直向上抛出,初速度为v1,经过时间t1落回地面,运动过程中小球的最大高度为h1;小球落地后,竖直向上弹起,初速度为v2,经过时间t2落回地面,运动过程中小球的最大高度为h2.若h1=1.21h2,则t1:t2= .
三、解答题
19.毛泽东故居景区有一商店销售一种纪念品,这种商品的成本价为10元/件,已知销售价不低于成本价,且物价部门规定这种商品的销售价不高于20元/件,市场调查发现,该商品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
20.在平面直角坐标系xOy中,有抛物线.
(1)若点在抛物线上,
①求抛物线的对称轴;
②若点也在抛物线上,求的取值范围;
(2)当时,有已知点,若抛物线与线段AB只有一个公共点,结合函数图象,求的取值范围.
21.体育测试时,九年级一名学生,双手扔实心球.已知实心球所经过的路线是某个二次函数图象的一部分,如果球出手处 点距离地面的高度为 ,当球运行的水平距离为 时,达到最大高度 的 处(如图),问该学生把实心球扔出多远?(结果保留根号)
22.如图,已知二次函数y=x2+bx+c图象经过点A(1,﹣2)和B(0,﹣5).
(1)求该二次函数的表达式及图象的顶点坐标;
(2)当y≤﹣2时,请根据图象直接写出x的取值范围.
23.中新社上海3月21日电(记者缪璐)21日在上海举行的2023年全国跳水冠军赛女子单人10米跳台决赛中,陈芋汐以416.25分的总分夺得冠军,全红婵位列第二,掌敏洁获得铜牌.在精彩的比赛过程中,全红婵选择了一个极具难度的207C(向后翻腾三周半抱膝).如图2所示,建立平面直角坐标系xOy.如果她从点A(3,10)起跳后的运动路线可以看作抛物线的一部分,从起跳到入水的过程中,她的竖直高度y(单位:米)与水平距离x(单位:米)近似满足函数关系式y=a(x﹣h)2+k(a<0).
(1)在平时训练完成一次跳水动作时,全红蝉的水平距离x与竖直高度y的几组数据如下:
水平距离x/m 0 3 3.5 4 4.5
竖直高度y/m 10 10 k 10 6.25
根据上述数据,直接写出k的值为 ,直接写出满足的函数关系式: ;
(2)比赛当天的某一次跳水中,全红婵的竖直高度y与水平距离x近似满足函数关系y=﹣5x2+40x﹣68,记她训练的入水点的水平距离为d1;比赛当天入水点的水平距离为d2,则d1 d2(填“>”“=”或“<”);
(3)在(2)的情况下,全红婵起跳后到达最高点B开始计时,若点B到水平面的距离为c,则她到水面的距离y与时间t之间近似满足y=﹣5t2+c,如果全红婵在达到最高点后需要1.6秒的时间才能完成极具难度的270C动作,请通过计算说明,她当天的比赛能否成功完成此动作?
答案解析部分
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】D
5.【答案】D
6.【答案】B
7.【答案】A
8.【答案】B
9.【答案】A
10.【答案】D
11.【答案】
12.【答案】2或
13.【答案】2
14.【答案】15
15.【答案】(1)或
(2)0或5或5或0
16.【答案】
17.【答案】
18.【答案】11:10
19.【答案】(1)解:设y与x的函数解析式为y=kx+b,
将(12,28)、(15,25)代入,得:
解得:,
所以y与x的函数解析式为y=﹣x+40(10≤x≤20);
(2)解:根据题意知,W=(x﹣10)y
=(x﹣10)(﹣x+40)
=﹣x2+50x﹣400
=﹣(x﹣25)2+225,
∵a=﹣1<0,
∴当x<25时,W随x的增大而增大,
∵10≤x≤20,
∴当x=20时,W取得最大值,最大值为200,
答:每件销售价为20元时,每天的销售利润最大,最大利润是200元.
20.【答案】(1)①点在抛物线上,,
,
抛物线的对称轴为直线;
②抛物线的对称轴为直线,
,
抛物线顶点坐标为,
点在抛物线上,
当时,,解得;
当时,,解得
综上所述,或.
(2)当时,,
点在抛物线与轴围成的图象的内部,
当时,,
当时,点在第一象限内,
点在抛物线与轴围成的图象的内部,
线段AB只有和在左侧的抛物线相交,
抛物线与线段AB恰有一个公共点,
当时,点在第一象限内,
点在抛物线与轴围成的图象的内部,
线段AB只有和在右侧的抛物线相交,
抛物线与线段AB恰有一个公共点,
或
即满足条件的的范围为或.
21.【答案】解:以 所在直线为 轴,过点 作 的垂线为 轴,建立平面直角坐标系,则有 ,如图所示:
设函数解析式为: ,则把点A代入得:
,解得: ,
∴函数解析式为 ,
令 ,则有 ,解得: (舍), ,
所以,该同学把实心球扔出 米.
22.【答案】(1)解:把A(1,-2)和B(0,-5)代入y=x2+bx+c得:
,
解得,
∴二次函数的表达式为y=x2+2x-5,
∵y=x2+2x﹣5=(x+1)2-6,
∴顶点坐标为(-1,-6);
(2)解:如图:
∵点A(1,-2)关于对称轴直线x=﹣1的对称点C(-3,-2),
∴当y≤-2时,x的范围是-3≤x≤1.
23.【答案】(1)11.25;y=﹣5(x﹣3.5)2+11.25
(2)<
(3)解:y=﹣5x2+40x﹣68=﹣5(x﹣4)2+12,
∴B(4,12),
∴c=12,
∴y=﹣5t2+12,
当t=1.6时,y=﹣5×1.62+12=﹣0.8,
∵﹣0.8<0,
即她在水面上无法完成此动作,
∴她当天的比赛不能成功完成此动作.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学苏科版九年级下册第5章二次函数重难点检测卷
一、选择题
1.关于二次函数,下列说法正确的是( )
A.函数图象的开口向下 B.函数图象的顶点坐标是
C.该函数的最大值是5 D.当时,y随x的增大而增大
2.如图,二次函数的图象与x轴交于,B两点,下列说法正确的是( )
A.抛物线的对称轴为直线
B.抛物线的顶点坐标为
C.A,B两点之间的距离为5
D.当时,y的值随x值的增大而增大
3.若点、都在二次函数的图象上,则a与b的大小关系( )
A. B. C. D.无法确定
4. 二次函数y=ax2+3x﹣1与x轴的交点个数是( )
A.2 B.1 C.0 D.不能确定
5.二次函数 的图象与x轴有交点,则k的取值范围是( )
A. B. 且
C. D. 且
6.如图,一名学生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是y=(x-10)(x+4),则铅球推出的距离OA=( )
A.14m B.10m C.7m D.4m
7.二次函数y=ax2+bx+1的图象与一次函数y=2ax+b在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
8.若一次函数y=(n+1)x+n的图象过第一、三、四象限,则函数y=nx2﹣nx( )
A.有最大值 B.有最大值
C.有最小值 D.有最小值
9.已知 和 均是以 为自变量的函数,当 时,函数值分别是 和 ,若存在实数 ,使得 ,则称函数 和 具有性质P。以下函数 和 具有性质P的是( )
A. 和 B. 和
C. 和 D. 和
10.如图,已知开口向上的抛物线与轴交于点,对称轴为直线.下列结论:①;②;③若关于的方程一定有两个不相等的实数根;④.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.把抛物线y=x2+1向右平移1个单位,所得新抛物线的表达式是 .
12. 关于的二次函数,在时有最大值6,则 .
13.如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米.水面下降1米时,水面的宽度为 米.
14.如图,王叔叔想用长为的栅栏,再借助房屋的外墙围成一个矩形羊圈,已知房屋外墙足够长,当矩形的边 时,羊圈的面积最大.
15.已知点是抛物线上一动点.
(1)当点M到y轴的距离不大于1时,b的取值范围是 ;
(2)当点M到直线的距离不大于时,b的取值范围是,则的值为 .
16.某广场要建一个圆形喷水池,计划在池中心位置竖直安装一根带有喷水头的水管,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m(如图).若水柱落地处离池中心的水平距离也为3m,则水管的设计高度应为 m.
17.下图是,二次函数的图象,若关于x的一元二次方程(t为实数)在的范围内有解,则t的取值范围是 .
18.以初速度v(单位:m/s)从地面竖直向上抛出小球,从抛出到落地的过程中(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=vt﹣4.9t2.现将某弹性小球从地面竖直向上抛出,初速度为v1,经过时间t1落回地面,运动过程中小球的最大高度为h1;小球落地后,竖直向上弹起,初速度为v2,经过时间t2落回地面,运动过程中小球的最大高度为h2.若h1=1.21h2,则t1:t2= .
三、解答题
19.毛泽东故居景区有一商店销售一种纪念品,这种商品的成本价为10元/件,已知销售价不低于成本价,且物价部门规定这种商品的销售价不高于20元/件,市场调查发现,该商品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
20.在平面直角坐标系xOy中,有抛物线.
(1)若点在抛物线上,
①求抛物线的对称轴;
②若点也在抛物线上,求的取值范围;
(2)当时,有已知点,若抛物线与线段AB只有一个公共点,结合函数图象,求的取值范围.
21.体育测试时,九年级一名学生,双手扔实心球.已知实心球所经过的路线是某个二次函数图象的一部分,如果球出手处 点距离地面的高度为 ,当球运行的水平距离为 时,达到最大高度 的 处(如图),问该学生把实心球扔出多远?(结果保留根号)
22.如图,已知二次函数y=x2+bx+c图象经过点A(1,﹣2)和B(0,﹣5).
(1)求该二次函数的表达式及图象的顶点坐标;
(2)当y≤﹣2时,请根据图象直接写出x的取值范围.
23.中新社上海3月21日电(记者缪璐)21日在上海举行的2023年全国跳水冠军赛女子单人10米跳台决赛中,陈芋汐以416.25分的总分夺得冠军,全红婵位列第二,掌敏洁获得铜牌.在精彩的比赛过程中,全红婵选择了一个极具难度的207C(向后翻腾三周半抱膝).如图2所示,建立平面直角坐标系xOy.如果她从点A(3,10)起跳后的运动路线可以看作抛物线的一部分,从起跳到入水的过程中,她的竖直高度y(单位:米)与水平距离x(单位:米)近似满足函数关系式y=a(x﹣h)2+k(a<0).
(1)在平时训练完成一次跳水动作时,全红蝉的水平距离x与竖直高度y的几组数据如下:
水平距离x/m 0 3 3.5 4 4.5
竖直高度y/m 10 10 k 10 6.25
根据上述数据,直接写出k的值为 ,直接写出满足的函数关系式: ;
(2)比赛当天的某一次跳水中,全红婵的竖直高度y与水平距离x近似满足函数关系y=﹣5x2+40x﹣68,记她训练的入水点的水平距离为d1;比赛当天入水点的水平距离为d2,则d1 d2(填“>”“=”或“<”);
(3)在(2)的情况下,全红婵起跳后到达最高点B开始计时,若点B到水平面的距离为c,则她到水面的距离y与时间t之间近似满足y=﹣5t2+c,如果全红婵在达到最高点后需要1.6秒的时间才能完成极具难度的270C动作,请通过计算说明,她当天的比赛能否成功完成此动作?
答案解析部分
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】D
5.【答案】D
6.【答案】B
7.【答案】A
8.【答案】B
9.【答案】A
10.【答案】D
11.【答案】
12.【答案】2或
13.【答案】2
14.【答案】15
15.【答案】(1)或
(2)0或5或5或0
16.【答案】
17.【答案】
18.【答案】11:10
19.【答案】(1)解:设y与x的函数解析式为y=kx+b,
将(12,28)、(15,25)代入,得:
解得:,
所以y与x的函数解析式为y=﹣x+40(10≤x≤20);
(2)解:根据题意知,W=(x﹣10)y
=(x﹣10)(﹣x+40)
=﹣x2+50x﹣400
=﹣(x﹣25)2+225,
∵a=﹣1<0,
∴当x<25时,W随x的增大而增大,
∵10≤x≤20,
∴当x=20时,W取得最大值,最大值为200,
答:每件销售价为20元时,每天的销售利润最大,最大利润是200元.
20.【答案】(1)①点在抛物线上,,
,
抛物线的对称轴为直线;
②抛物线的对称轴为直线,
,
抛物线顶点坐标为,
点在抛物线上,
当时,,解得;
当时,,解得
综上所述,或.
(2)当时,,
点在抛物线与轴围成的图象的内部,
当时,,
当时,点在第一象限内,
点在抛物线与轴围成的图象的内部,
线段AB只有和在左侧的抛物线相交,
抛物线与线段AB恰有一个公共点,
当时,点在第一象限内,
点在抛物线与轴围成的图象的内部,
线段AB只有和在右侧的抛物线相交,
抛物线与线段AB恰有一个公共点,
或
即满足条件的的范围为或.
21.【答案】解:以 所在直线为 轴,过点 作 的垂线为 轴,建立平面直角坐标系,则有 ,如图所示:
设函数解析式为: ,则把点A代入得:
,解得: ,
∴函数解析式为 ,
令 ,则有 ,解得: (舍), ,
所以,该同学把实心球扔出 米.
22.【答案】(1)解:把A(1,-2)和B(0,-5)代入y=x2+bx+c得:
,
解得,
∴二次函数的表达式为y=x2+2x-5,
∵y=x2+2x﹣5=(x+1)2-6,
∴顶点坐标为(-1,-6);
(2)解:如图:
∵点A(1,-2)关于对称轴直线x=﹣1的对称点C(-3,-2),
∴当y≤-2时,x的范围是-3≤x≤1.
23.【答案】(1)11.25;y=﹣5(x﹣3.5)2+11.25
(2)<
(3)解:y=﹣5x2+40x﹣68=﹣5(x﹣4)2+12,
∴B(4,12),
∴c=12,
∴y=﹣5t2+12,
当t=1.6时,y=﹣5×1.62+12=﹣0.8,
∵﹣0.8<0,
即她在水面上无法完成此动作,
∴她当天的比赛不能成功完成此动作.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
