北师大版八年级数学下册第六章 平行四边形 难点详解专项训练练习题(含解析)
文档属性
| 名称 | 北师大版八年级数学下册第六章 平行四边形 难点详解专项训练练习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 357.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 00:00:00 | ||
图片预览



文档简介
北师大版八年级数学下册第六章平行四边形专项训练
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如果一个多边形的外角和等于其内角和的2倍,那么这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
2、如图,在正五边形ABCDE中,连接AD,则∠DAE的度数为( )
A.46° B.56° C.36° D.26°
3、如图,点O是 ABCD的对称中心,l是过点O的任意一条直线,它将平行四边形分成甲、乙两部分,在这个图形上做扎针试验,则针头扎在甲、乙两个区域的可能性的大小是( )
A.甲大 B.乙大 C.一样大 D.无法确定
4、若一个多边形的每一个内角均为120°,则下列说法错误的是( )
A.这个多边形的内角和为720° B.这个多边形的边数为6
C.这个多边形是正多边形 D.这个多边形的外角和为360°
5、如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=( )
A.90° B.180° C.270° D.360°
6、平行四边形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OA=OC=,则点B的坐标为( )
A.(,1) B.(1,) C.(+1,1) D.(1,+1)
7、如图,桐桐从A点出发,前进3m到点B处后向右转20°,再前进3m到点C处后又向右转20°,…,这样一直走下去,她第一次回到出发点A时,一共走了( )
A.100m B.90m C.54m D.60m
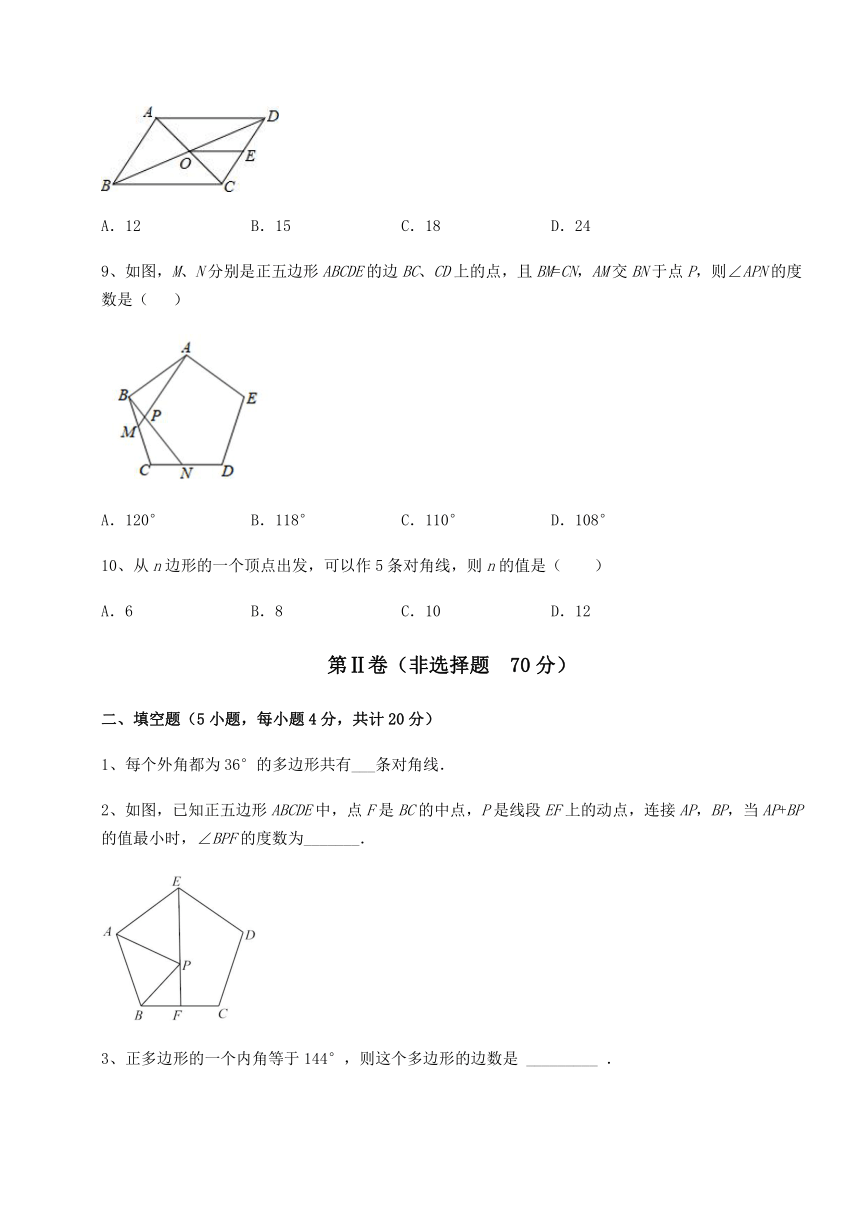
8、如图,平行四边形ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是( )
A.12 B.15 C.18 D.24
9、如图,M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P,则∠APN的度数是( )
A.120° B.118° C.110° D.108°
10、从n边形的一个顶点出发,可以作5条对角线,则n的值是( )
A.6 B.8 C.10 D.12
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、每个外角都为36°的多边形共有___条对角线.
2、如图,已知正五边形ABCDE中,点F是BC的中点,P是线段EF上的动点,连接AP,BP,当AP+BP的值最小时,∠BPF的度数为_______.
3、正多边形的一个内角等于144°,则这个多边形的边数是 _________ .
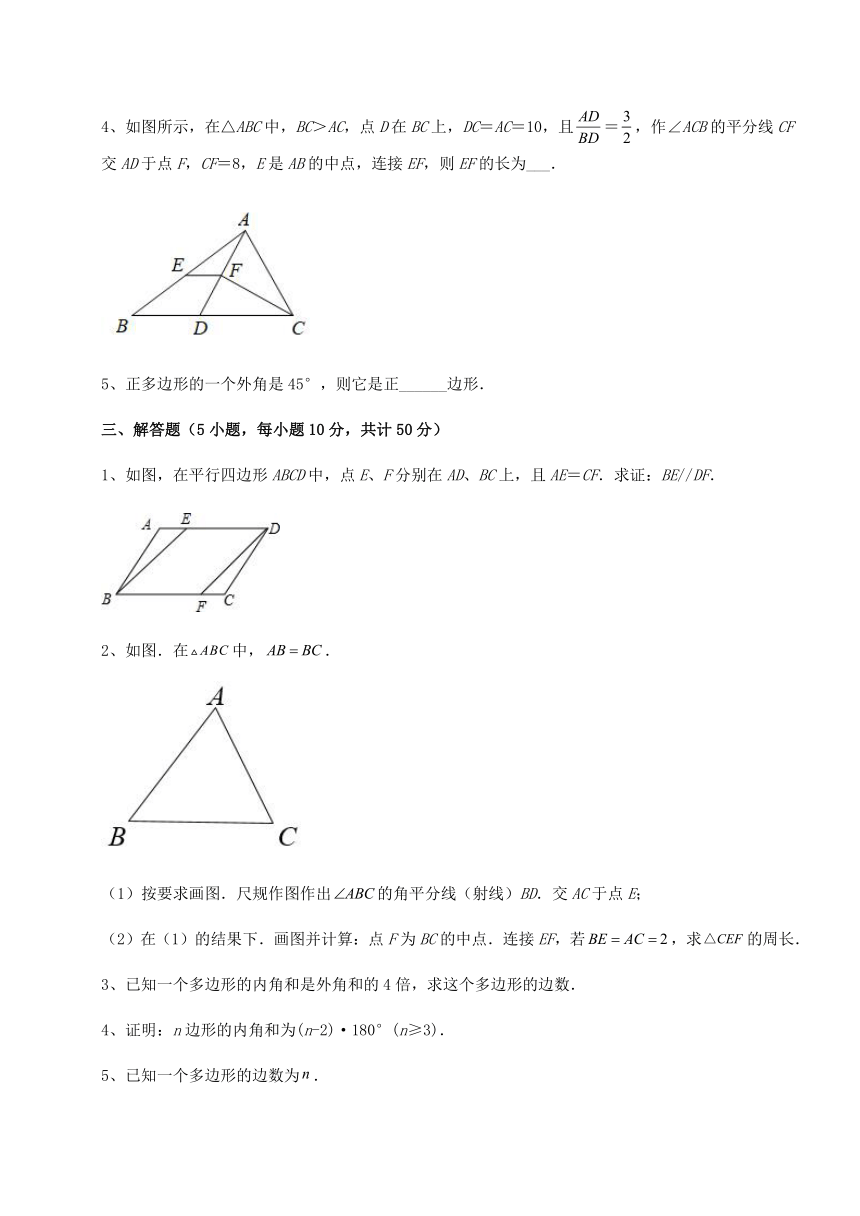
4、如图所示,在△ABC中,BC>AC,点D在BC上,DC=AC=10,且=,作∠ACB的平分线CF交AD于点F,CF=8,E是AB的中点,连接EF,则EF的长为___.
5、正多边形的一个外角是45°,则它是正______边形.
三、解答题(5小题,每小题10分,共计50分)
1、如图,在平行四边形ABCD中,点E、F分别在AD、BC上,且AE=CF.求证:BE//DF.
2、如图.在中,.
(1)按要求画图.尺规作图作出的角平分线(射线)BD.交AC于点E;
(2)在(1)的结果下.画图并计算:点F为BC的中点.连接EF,若,求的周长.
3、已知一个多边形的内角和是外角和的4倍,求这个多边形的边数.
4、证明:n边形的内角和为(n-2)·180°(n≥3).
5、已知一个多边形的边数为.
(1)若,求这个多边形的内角和.
(2)若这个多边形的内角和的比一个四边形的外角和多,求的值.
-参考答案-
一、单选题
1、A
【分析】
多边形的外角和是360度,多边形的外角和是内角和的2倍,则多边形的内角和是180度,则这个多边形一定是三角形.
【详解】
解:多边形的外角和是360度,
又多边形的外角和是内角和的2倍,
多边形的内角和是180度,
这个多边形是三角形.
故选:A.
【点睛】
考查了多边形的外角和定理,解题的关键是掌握多边形的外角和定理.
2、C
【分析】
在等腰三角形中,求出的度数即可解决问题.
【详解】
在正五边形中,,
是等腰三角形,
.
故选:C.
【点睛】
本题主要考查等腰三角形的性质以及正多边形内角,解答本题的关键是求出正五边形的内角,此题基础题,比较简单.
3、C
【分析】
如图,连接 记过的直线交于 则为的中点,再证明 可得 从而可得答案.
【详解】
解:如图,连接 记过的直线交于
为 ABCD的对称中心,
为的中点,
同理:
所以针头扎在甲、乙两个区域的可能性的大小是一样的,
故选C
【点睛】
本题考查的是全等三角形的判定与性质,平行四边形的性质,随机事件发生的可能性的大小,几何概率的意义,理解几何概率的意义是解本题的关键.
4、C
【分析】
先根据多边形的外角和求出这个多边形的边数,再根据多边形的内角和、正多边形的定义即可得.
【详解】
解:多边形的每一个内角均为,
这个多边形的每一个外角均为,
这个多边形的边数为,则选项B说法正确;
这个多边形的内角和为,则选项A说法正确;
多边形的外角和为,
选项D说法正确;
各边相等,各内角也相等的多边形叫做正多边形,
选项C说法错误;
故选:C.
【点睛】
本题考查了多边形的内角和与外角和、正多边形的定义,熟练掌握多边形的内角和与外角和是解题关键.
5、C
【分析】
首先根据三角形内角和定理算出的度数,再根据四边形内角和为,计算出的度数.
【详解】
解:,
,
,
,
故选:C.
【点睛】
本题主要考查了三角形内角和定理,多边形内角和定理,解题的关键是利用三角形的内角和,四边形的内角和.
6、C
【分析】
作,求得、的长度,即可求解.
【详解】
解:作,如下图:
则
在平行四边形中,,
∴
∴为等腰直角三角形
则,解得
∴
故选:C
【点睛】
此题考查了平行四边形的性质,等腰直角三角形的性质以及勾股定理,解题的关键是灵活运用相关性质进行求解.
7、C
【分析】
根据多边形的外角和及每一个外角的度数,可求出多边形的边数,再根据题意求出正多边形的周长即可.
【详解】
解:由题意可知,当她第一次回到出发点A时,所走过的图形是一个正多边形,
由于正多边形的外角和是360°,且每一个外角为20°,
360°÷20°=18,
所以它是一个正18边形,
因此所走的路程为18×3=54(m),
故选:C.
【点睛】
本题考查了多边形的内角与外角,能熟记多边形的外角和定理是解此题的关键,注意:多边形的外角和=360°.
8、B
【分析】
根据平行四边形的对边相等和对角线互相平分可得,OB=OD,又因为E点是CD的中点,可得OE是△BCD的中位线,可得OE=BC,所以易求△DOE的周长.
【详解】
解:∵ ABCD的周长为36,
∴2(BC+CD)=36,则BC+CD=18.
∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=12,
∴OD=OB=BD=6.
又∵点E是CD的中点,
∴OE是△BCD的中位线,DE=CD,
∴OE=BC,
∴△DOE的周长=OD+OE+DE=BD+(BC+CD)=6+9=15,
故选:B.
【点睛】
本题考查了三角形中位线定理、平行四边形的性质.解题时,利用了“平行四边形对角线互相平分”、“平行四边形的对边相等”的性质.
9、D
【分析】
由五边形的性质得出AB=BC,∠ABM=∠C,证明△ABM≌△BCN,得出∠BAM=∠CBN,由∠BAM+∠ABP=∠APN,即可得出∠APN=∠ABC,即可得出结果.
【详解】
解:∵五边形ABCDE为正五边形,
∴AB=BC,∠ABM=∠C,
在△ABM和△BCN中
,
∴△ABM≌△BCN(SAS),
∴∠BAM=∠CBN,
∵∠BAM+∠ABP=∠APN,
∴∠CBN+∠ABP=∠APN=∠ABC=
∴∠APN的度数为108°;
故选:D.
【点睛】
本题考查了全等三角形的判定与性质、多边形的内角和定理;熟练掌握五边形的形状,证明三角形全等是解决问题的关键.
10、B
【分析】
根据从边形的一个顶点出发可以作条对角线即可得.
【详解】
解:由题意得:,
解得,
故选:B.
【点睛】
本题考查了多边形的对角线问题,熟练掌握“从边形的一个顶点出发可以作条对角线”是解题关键.
二、填空题
1、35
【分析】
设这个多边形为n边形,然后根据多边形外角和为360度以及多边形对角线公式进行求解即可.
【详解】
解:设这个多边形为n边形,
由题意得:,
∴,
∴这个多边形的对角线条数条,
故答案为:35.
【点睛】
本题主要考查了多边形外角和,多边形对角线条数,解题的关键在于能够熟练掌握相关知识进行求解.
2、54°
【分析】
如图,连接AC,PC,设AC交EF于点P′,连接BP′.证明当点P与P′重合时,PA+PB的值最小,求出∠P′BC可得结论.
【详解】
解:如图,连接AC,PC,设AC交EF于点P′,连接BP′.
∵正五边形ABCDE中,点F是BC的中点,
∵EF⊥BC,
∴B,C关于EF对称,
∴PB=PC,
∵PA+PB=PA+PC≥AC,
∴当点P与P′重合时,PA+PB的值最小,
∵ABCDE是正五边形,
∴BA=BC,∠ABC=108°,
∴∠BAC=∠BCA=36°,
∵P′B=CP′,
∴∠P′BC=∠P′CB=36°,
∵∠EFB=90°,
∴∠BP′F=90°﹣∠P′BC=90°﹣36°=54°.
故答案为:54°.
【点睛】
本题考查正多边形,轴对称﹣最短问题等知识,解题的关键是学会利用轴对称解决最短问题,属于中考常考题型.
3、10
【分析】
先根据已知条件设出正多边形的边数,再根据正多边形的计算公式得出结果即可.
【详解】
解:设这个正多边形是正n边形,根据题意得:
(n-2)×180°=144°n,
解得:n=10.
故答案为:10.
【点睛】
本题考查了正多边形的内角,在解题时要根据正多边形的内角和公式列出式子是本题的关键.
4、4
【分析】
根据等腰三角形的性质得到F为AD的中点,CF⊥AD,根据勾股定理得到DF==6,根据三角形的中位线定理即可得到结论.
【详解】
解:∵DC=AC=10,∠ACB的平分线CF交AD于F,
∴F为AD的中点,CF⊥AD,
∴∠CFD=90°,
∵DC=10,CF=8,
∴DF==6,
∴AD=2DF=12,
∵,
∴BD=8,
∵点E是AB的中点,
∴EF为△ABD的中位线,
∴EF=BD=4,
故答案为:4.
【点睛】
本题考查了三角形的中位线定理,等腰三角形的性质,勾股定理,证得EF是△ABD的中位线是解题的关键.
5、八
【分析】
利用任意多边形的外角和均为360°,正多边形的每个外角相等即可求出答案.
【详解】
360÷45=8.
故它是正八边形.
故答案为:八.
【点睛】
此题主要考查了多边形的外角和,利用任意凸多边形的外角和均为360°,正多边形的每个外角相等即可求出答案.
三、解答题
1、见解析
【分析】
先求出DE=BF,再证明四边形BEDF是平行四边形,即可得出结论.
【详解】
证明:∵四边形ABCD是平行四边形
∴AD=BC,AD//BC,
∵AE=CF,
∴DE=BF,
又∵DE//BF,
∴四边形BEDF是平行四边形,
∴BE//DF.
【点睛】
本题考查了平行四边形的判定与性质;熟练掌握平行四边形的判定方法,证明四边形是平行四边形是解决问题的关键.
2、(1)见解析;(2)
【分析】
(1)根据角平分线的尺规作图方式进行解答即可;
(2)根据等腰三角形三线合一以及三角形中位线的知识进行解答即可.
【详解】
解:(1)如图即为所作:
;
(2)∵,平分,
∴,
∴,
在中,
,
∵是的中点,为BC的中点,
∴为的中位线,
∴,,
∴的周长=.
【点睛】
本题考查了尺规作图-角平分线,等腰三角形三线合一的性质,以及三角形中位线的性质,熟练掌握以上性质是解本题的关键.
3、这个多边形的边数是10.
【分析】
多边形的外角和是360°,内角和是它的外角和的4倍,则内角和为4×360=1440度.n边形的内角和可以表示成(n-2) 180°,设这个多边形的边数是n,即可得到方程,从而求出边数.
【详解】
解:设这个多边形的边数为n,
由题意得:(n-2)×180°=4×360°,
解得n=10,
故这个多边形的边数是10.
【点睛】
此题主要考查了多边形的外角和,内角和公式,做题的关键是正确把握内角和公式为:(n-2) 180°,外角和为360°.
4、见解析
【分析】
在n边形内任取一点O,连接O与各顶点的线段把n边形分成了n个三角形,然后利用n个三角形的面积减去以O为公共顶点的n个角的和,即可求证.
【详解】
已知: n边形A1A2……An,
求证: ,
证明:如图,在n边形内任取一点O,连接O与各顶点的线段把n边形分成了n个三角形,
∵n个三角形内角和为n·180°,以O为公共顶点的n个角的和360°(即一个周角),
∴n边形内角和为 .
【点睛】
本题主要考查了多边形的内角和,做适当辅助线,得到n边形的内角和等于n个三角形的面积减去以O为公共顶点的n个角的和是解题的关键.
5、(1);(2)12
【分析】
(1)把,代入多边形内角和公式求解即可;
(2)根据多边形内角和公式及多边形外角和为,列出一元一次方程求解即可.
【详解】
解:(1)当时,,
∴这个多边形的内角和为.
(2)由题意,得,
解得:,
∴的值为12.
【点睛】
本题考查了多边形的内角和与外角和问题及一元一次方程应用,解题的关键是牢记多边形的内角和与外角和.
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如果一个多边形的外角和等于其内角和的2倍,那么这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
2、如图,在正五边形ABCDE中,连接AD,则∠DAE的度数为( )
A.46° B.56° C.36° D.26°
3、如图,点O是 ABCD的对称中心,l是过点O的任意一条直线,它将平行四边形分成甲、乙两部分,在这个图形上做扎针试验,则针头扎在甲、乙两个区域的可能性的大小是( )
A.甲大 B.乙大 C.一样大 D.无法确定
4、若一个多边形的每一个内角均为120°,则下列说法错误的是( )
A.这个多边形的内角和为720° B.这个多边形的边数为6
C.这个多边形是正多边形 D.这个多边形的外角和为360°
5、如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=( )
A.90° B.180° C.270° D.360°
6、平行四边形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OA=OC=,则点B的坐标为( )
A.(,1) B.(1,) C.(+1,1) D.(1,+1)
7、如图,桐桐从A点出发,前进3m到点B处后向右转20°,再前进3m到点C处后又向右转20°,…,这样一直走下去,她第一次回到出发点A时,一共走了( )
A.100m B.90m C.54m D.60m
8、如图,平行四边形ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是( )
A.12 B.15 C.18 D.24
9、如图,M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P,则∠APN的度数是( )
A.120° B.118° C.110° D.108°
10、从n边形的一个顶点出发,可以作5条对角线,则n的值是( )
A.6 B.8 C.10 D.12
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、每个外角都为36°的多边形共有___条对角线.
2、如图,已知正五边形ABCDE中,点F是BC的中点,P是线段EF上的动点,连接AP,BP,当AP+BP的值最小时,∠BPF的度数为_______.
3、正多边形的一个内角等于144°,则这个多边形的边数是 _________ .
4、如图所示,在△ABC中,BC>AC,点D在BC上,DC=AC=10,且=,作∠ACB的平分线CF交AD于点F,CF=8,E是AB的中点,连接EF,则EF的长为___.
5、正多边形的一个外角是45°,则它是正______边形.
三、解答题(5小题,每小题10分,共计50分)
1、如图,在平行四边形ABCD中,点E、F分别在AD、BC上,且AE=CF.求证:BE//DF.
2、如图.在中,.
(1)按要求画图.尺规作图作出的角平分线(射线)BD.交AC于点E;
(2)在(1)的结果下.画图并计算:点F为BC的中点.连接EF,若,求的周长.
3、已知一个多边形的内角和是外角和的4倍,求这个多边形的边数.
4、证明:n边形的内角和为(n-2)·180°(n≥3).
5、已知一个多边形的边数为.
(1)若,求这个多边形的内角和.
(2)若这个多边形的内角和的比一个四边形的外角和多,求的值.
-参考答案-
一、单选题
1、A
【分析】
多边形的外角和是360度,多边形的外角和是内角和的2倍,则多边形的内角和是180度,则这个多边形一定是三角形.
【详解】
解:多边形的外角和是360度,
又多边形的外角和是内角和的2倍,
多边形的内角和是180度,
这个多边形是三角形.
故选:A.
【点睛】
考查了多边形的外角和定理,解题的关键是掌握多边形的外角和定理.
2、C
【分析】
在等腰三角形中,求出的度数即可解决问题.
【详解】
在正五边形中,,
是等腰三角形,
.
故选:C.
【点睛】
本题主要考查等腰三角形的性质以及正多边形内角,解答本题的关键是求出正五边形的内角,此题基础题,比较简单.
3、C
【分析】
如图,连接 记过的直线交于 则为的中点,再证明 可得 从而可得答案.
【详解】
解:如图,连接 记过的直线交于
为 ABCD的对称中心,
为的中点,
同理:
所以针头扎在甲、乙两个区域的可能性的大小是一样的,
故选C
【点睛】
本题考查的是全等三角形的判定与性质,平行四边形的性质,随机事件发生的可能性的大小,几何概率的意义,理解几何概率的意义是解本题的关键.
4、C
【分析】
先根据多边形的外角和求出这个多边形的边数,再根据多边形的内角和、正多边形的定义即可得.
【详解】
解:多边形的每一个内角均为,
这个多边形的每一个外角均为,
这个多边形的边数为,则选项B说法正确;
这个多边形的内角和为,则选项A说法正确;
多边形的外角和为,
选项D说法正确;
各边相等,各内角也相等的多边形叫做正多边形,
选项C说法错误;
故选:C.
【点睛】
本题考查了多边形的内角和与外角和、正多边形的定义,熟练掌握多边形的内角和与外角和是解题关键.
5、C
【分析】
首先根据三角形内角和定理算出的度数,再根据四边形内角和为,计算出的度数.
【详解】
解:,
,
,
,
故选:C.
【点睛】
本题主要考查了三角形内角和定理,多边形内角和定理,解题的关键是利用三角形的内角和,四边形的内角和.
6、C
【分析】
作,求得、的长度,即可求解.
【详解】
解:作,如下图:
则
在平行四边形中,,
∴
∴为等腰直角三角形
则,解得
∴
故选:C
【点睛】
此题考查了平行四边形的性质,等腰直角三角形的性质以及勾股定理,解题的关键是灵活运用相关性质进行求解.
7、C
【分析】
根据多边形的外角和及每一个外角的度数,可求出多边形的边数,再根据题意求出正多边形的周长即可.
【详解】
解:由题意可知,当她第一次回到出发点A时,所走过的图形是一个正多边形,
由于正多边形的外角和是360°,且每一个外角为20°,
360°÷20°=18,
所以它是一个正18边形,
因此所走的路程为18×3=54(m),
故选:C.
【点睛】
本题考查了多边形的内角与外角,能熟记多边形的外角和定理是解此题的关键,注意:多边形的外角和=360°.
8、B
【分析】
根据平行四边形的对边相等和对角线互相平分可得,OB=OD,又因为E点是CD的中点,可得OE是△BCD的中位线,可得OE=BC,所以易求△DOE的周长.
【详解】
解:∵ ABCD的周长为36,
∴2(BC+CD)=36,则BC+CD=18.
∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=12,
∴OD=OB=BD=6.
又∵点E是CD的中点,
∴OE是△BCD的中位线,DE=CD,
∴OE=BC,
∴△DOE的周长=OD+OE+DE=BD+(BC+CD)=6+9=15,
故选:B.
【点睛】
本题考查了三角形中位线定理、平行四边形的性质.解题时,利用了“平行四边形对角线互相平分”、“平行四边形的对边相等”的性质.
9、D
【分析】
由五边形的性质得出AB=BC,∠ABM=∠C,证明△ABM≌△BCN,得出∠BAM=∠CBN,由∠BAM+∠ABP=∠APN,即可得出∠APN=∠ABC,即可得出结果.
【详解】
解:∵五边形ABCDE为正五边形,
∴AB=BC,∠ABM=∠C,
在△ABM和△BCN中
,
∴△ABM≌△BCN(SAS),
∴∠BAM=∠CBN,
∵∠BAM+∠ABP=∠APN,
∴∠CBN+∠ABP=∠APN=∠ABC=
∴∠APN的度数为108°;
故选:D.
【点睛】
本题考查了全等三角形的判定与性质、多边形的内角和定理;熟练掌握五边形的形状,证明三角形全等是解决问题的关键.
10、B
【分析】
根据从边形的一个顶点出发可以作条对角线即可得.
【详解】
解:由题意得:,
解得,
故选:B.
【点睛】
本题考查了多边形的对角线问题,熟练掌握“从边形的一个顶点出发可以作条对角线”是解题关键.
二、填空题
1、35
【分析】
设这个多边形为n边形,然后根据多边形外角和为360度以及多边形对角线公式进行求解即可.
【详解】
解:设这个多边形为n边形,
由题意得:,
∴,
∴这个多边形的对角线条数条,
故答案为:35.
【点睛】
本题主要考查了多边形外角和,多边形对角线条数,解题的关键在于能够熟练掌握相关知识进行求解.
2、54°
【分析】
如图,连接AC,PC,设AC交EF于点P′,连接BP′.证明当点P与P′重合时,PA+PB的值最小,求出∠P′BC可得结论.
【详解】
解:如图,连接AC,PC,设AC交EF于点P′,连接BP′.
∵正五边形ABCDE中,点F是BC的中点,
∵EF⊥BC,
∴B,C关于EF对称,
∴PB=PC,
∵PA+PB=PA+PC≥AC,
∴当点P与P′重合时,PA+PB的值最小,
∵ABCDE是正五边形,
∴BA=BC,∠ABC=108°,
∴∠BAC=∠BCA=36°,
∵P′B=CP′,
∴∠P′BC=∠P′CB=36°,
∵∠EFB=90°,
∴∠BP′F=90°﹣∠P′BC=90°﹣36°=54°.
故答案为:54°.
【点睛】
本题考查正多边形,轴对称﹣最短问题等知识,解题的关键是学会利用轴对称解决最短问题,属于中考常考题型.
3、10
【分析】
先根据已知条件设出正多边形的边数,再根据正多边形的计算公式得出结果即可.
【详解】
解:设这个正多边形是正n边形,根据题意得:
(n-2)×180°=144°n,
解得:n=10.
故答案为:10.
【点睛】
本题考查了正多边形的内角,在解题时要根据正多边形的内角和公式列出式子是本题的关键.
4、4
【分析】
根据等腰三角形的性质得到F为AD的中点,CF⊥AD,根据勾股定理得到DF==6,根据三角形的中位线定理即可得到结论.
【详解】
解:∵DC=AC=10,∠ACB的平分线CF交AD于F,
∴F为AD的中点,CF⊥AD,
∴∠CFD=90°,
∵DC=10,CF=8,
∴DF==6,
∴AD=2DF=12,
∵,
∴BD=8,
∵点E是AB的中点,
∴EF为△ABD的中位线,
∴EF=BD=4,
故答案为:4.
【点睛】
本题考查了三角形的中位线定理,等腰三角形的性质,勾股定理,证得EF是△ABD的中位线是解题的关键.
5、八
【分析】
利用任意多边形的外角和均为360°,正多边形的每个外角相等即可求出答案.
【详解】
360÷45=8.
故它是正八边形.
故答案为:八.
【点睛】
此题主要考查了多边形的外角和,利用任意凸多边形的外角和均为360°,正多边形的每个外角相等即可求出答案.
三、解答题
1、见解析
【分析】
先求出DE=BF,再证明四边形BEDF是平行四边形,即可得出结论.
【详解】
证明:∵四边形ABCD是平行四边形
∴AD=BC,AD//BC,
∵AE=CF,
∴DE=BF,
又∵DE//BF,
∴四边形BEDF是平行四边形,
∴BE//DF.
【点睛】
本题考查了平行四边形的判定与性质;熟练掌握平行四边形的判定方法,证明四边形是平行四边形是解决问题的关键.
2、(1)见解析;(2)
【分析】
(1)根据角平分线的尺规作图方式进行解答即可;
(2)根据等腰三角形三线合一以及三角形中位线的知识进行解答即可.
【详解】
解:(1)如图即为所作:
;
(2)∵,平分,
∴,
∴,
在中,
,
∵是的中点,为BC的中点,
∴为的中位线,
∴,,
∴的周长=.
【点睛】
本题考查了尺规作图-角平分线,等腰三角形三线合一的性质,以及三角形中位线的性质,熟练掌握以上性质是解本题的关键.
3、这个多边形的边数是10.
【分析】
多边形的外角和是360°,内角和是它的外角和的4倍,则内角和为4×360=1440度.n边形的内角和可以表示成(n-2) 180°,设这个多边形的边数是n,即可得到方程,从而求出边数.
【详解】
解:设这个多边形的边数为n,
由题意得:(n-2)×180°=4×360°,
解得n=10,
故这个多边形的边数是10.
【点睛】
此题主要考查了多边形的外角和,内角和公式,做题的关键是正确把握内角和公式为:(n-2) 180°,外角和为360°.
4、见解析
【分析】
在n边形内任取一点O,连接O与各顶点的线段把n边形分成了n个三角形,然后利用n个三角形的面积减去以O为公共顶点的n个角的和,即可求证.
【详解】
已知: n边形A1A2……An,
求证: ,
证明:如图,在n边形内任取一点O,连接O与各顶点的线段把n边形分成了n个三角形,
∵n个三角形内角和为n·180°,以O为公共顶点的n个角的和360°(即一个周角),
∴n边形内角和为 .
【点睛】
本题主要考查了多边形的内角和,做适当辅助线,得到n边形的内角和等于n个三角形的面积减去以O为公共顶点的n个角的和是解题的关键.
5、(1);(2)12
【分析】
(1)把,代入多边形内角和公式求解即可;
(2)根据多边形内角和公式及多边形外角和为,列出一元一次方程求解即可.
【详解】
解:(1)当时,,
∴这个多边形的内角和为.
(2)由题意,得,
解得:,
∴的值为12.
【点睛】
本题考查了多边形的内角和与外角和问题及一元一次方程应用,解题的关键是牢记多边形的内角和与外角和.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
