第二十六章 反比例函数重难点检测卷(含答案)
文档属性
| 名称 | 第二十六章 反比例函数重难点检测卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 799.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学人教版九年级下册第二十六章反比例函数重难点检测卷
一、选择题
1.函数 和y=-kx+2(k≠0); 在同一平面直角坐标系中的图象可能是 ( )
A. B.
C. D.
2.下列关于反比例函数 的说法,错误的是( )
A.图象经过点(1,-3) B.图象位于第二、四象限
C.图象关于直线y=x对称 D.y随x的增大而增大
3.某校科技小组进行野外考察,利用铺垫木板的方式,通过了一片湿泥地,他们发现:当人和木板对湿泥地的压力一定时,人和木板对地面的压强 p(Pa)随着木板面积S(m )的变化而变化,其关系式为 p 如果人和木板对湿泥地的压力 F 合计600 N,那么下列说法正确的是 ( )
A.p是S的正比例函数
B.当S越来越大时,p也越来越大
C.若压强不超过6000 Pa,则木板面积最大为 0.1m
D.当木板面积为0.2m 时,压强是3000 Pa
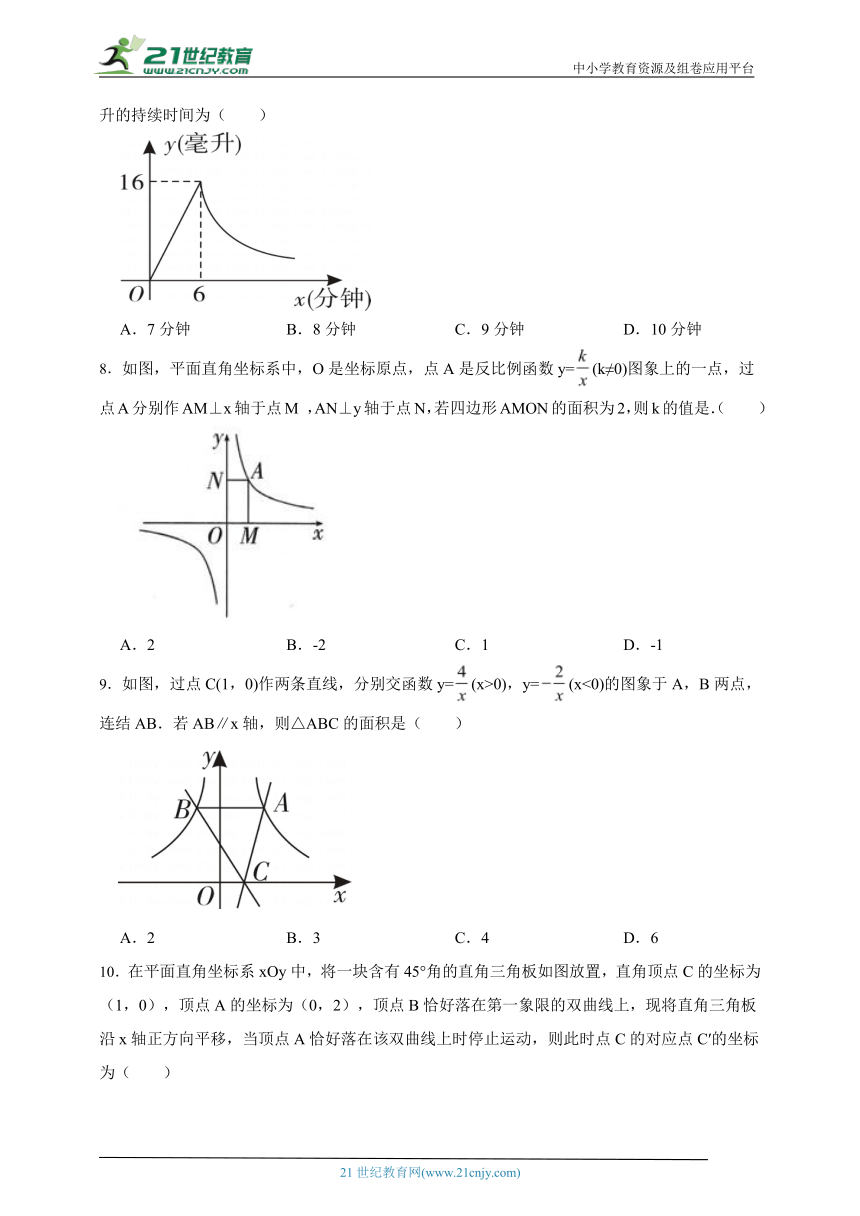
4. 某村耕地总面积为 50 公顷,且该村人均耕地面积y(公顷)与总人口x(人)的函数图象如图所示,则下列说法正确的是( )
A.该村人均耕地面积随总人口的增多而增多
B.该村人均耕地面积y与总人口x成正比例
C.若该村人均耕地面积为0.2公顷,则总人口为1000人
D.当该村总人口为50人时,人均耕地面积为1公顷
5.在同一平面直角坐标系中,一次函数+b与反比例函数(k k ≠0,x>0)的图象如图所示,则当 y >y 时,自变量x(x>0)的取值范围是( )
A.x<1 B.x>3 C.06.如图,函数. y=kx+b(k≠0)与的图象相交于 A(-2,3),B两点,则不等式 的解为( )
A.x>-2 B.-21
C.x>1 D.x<-2或07.某校工作人员对教室进行消毒时,室内每立方米空气中的含药量y(毫升)与喷洒消毒液的时间x(分钟)成正比例关系,喷洒完成后,y与x成反比例关系(如图所示).已知喷洒消毒液用时6分钟,此时室内每立方米空气中的含药量为16毫升.问室内每立方米空气中的含药量不低于8毫升的持续时间为( )
A.7分钟 B.8分钟 C.9分钟 D.10分钟
8.如图,平面直角坐标系中,O是坐标原点,点A是反比例函数y=(k≠0)图象上的一点,过点A分别作AM⊥x轴于点M ,AN⊥y轴于点N,若四边形AMON的面积为2,则k的值是.( )
A.2 B.-2 C.1 D.-1
9.如图,过点C(1,0)作两条直线,分别交函数y=(x>0),y=(x<0)的图象于A,B两点,连结AB.若AB∥x轴,则△ABC的面积是( )
A.2 B.3 C.4 D.6
10.在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
A.( ,0) B.(2,0)
C.( ,0) D.(3,0)
二、填空题
11. 当温度不变时,气球内气体的压强 p(kPa)是气体体积V(m )的函数,下表记录了一组实验数据:
V(m ) 1 1.5 2 2.5 3
p(kPa) 96 64 48 38.4 32
p关于V的函数表达式可能是 。
12.若点(2,m),(2,n)分别在反比例函数和 的图象上,则 m 和 n 的大小关系是m n(填“>”“<”或“=”).
13.已知点 A(-2,m)在一个反比例函数的图象上,点 A'与点 A 关于 y轴对称.若点 A'在正比例函数的图象上,则这个反比例函数的表达式为 .当x>2时,反比例函数值 y的取值范围是 .
14.如图, 已知点A(2,3),B(0,2),点 A 在反比例函数 的图象上,作射线 AB,再将射线 AB绕点 A 按逆时针方向旋转 45°,交反比例函数的图象于点 C,则点 C 的坐标为 .
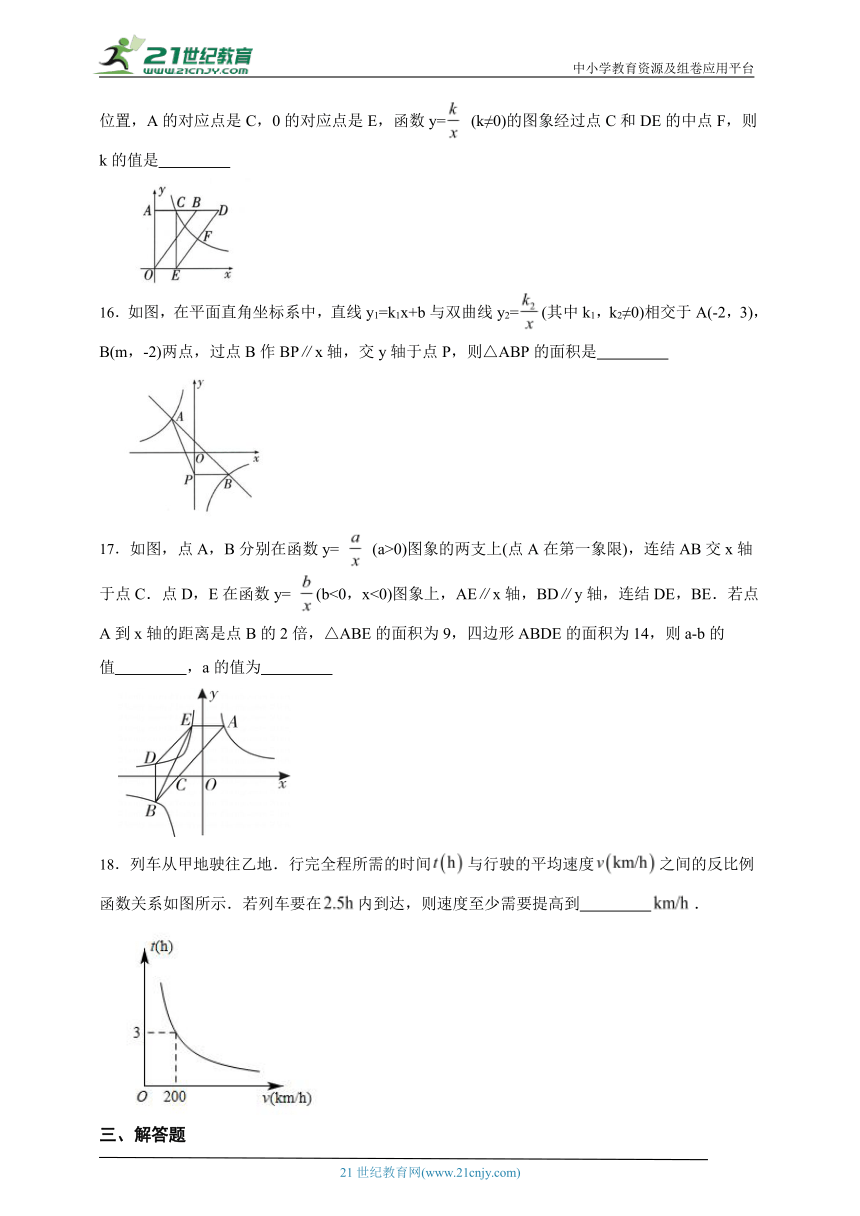
15.如图,在平面直角坐标系xOy中,点A(0,4),B(3,4) ,将△ABO向右平移到△CDE的位置,A的对应点是C,0的对应点是E,函数y= (k≠0)的图象经过点C和DE的中点F,则k的值是
16.如图,在平面直角坐标系中,直线y1=k1x+b与双曲线y2=(其中k1,k2≠0)相交于A(-2,3),B(m,-2)两点,过点B作BP∥x轴,交y轴于点P,则△ABP的面积是
17.如图,点A,B分别在函数y= (a>0)图象的两支上(点A在第一象限),连结AB交x轴于点C.点D,E在函数y= (b<0,x<0)图象上,AE∥x轴,BD∥y轴,连结DE,BE.若点A到x轴的距离是点B的2倍,△ABE的面积为9,四边形ABDE的面积为14,则a-b的值 ,a的值为
18.列车从甲地驶往乙地.行完全程所需的时间与行驶的平均速度之间的反比例函数关系如图所示.若列车要在内到达,则速度至少需要提高到 .
三、解答题
19.已知y是x的反比例函数,且当x=2时,y=6.
(1)求y关于x的函数表达式.
(2)当x=4时,求y的值.
20.如图,老李想利用一段5m 长的墙(图中 EF),建一个面积为32 m 的矩形猪圈,另外三面(图中 AB,BC,CD)需要自己修建.老李准备了可以修建20 m墙的材料(可以不用完).
(1)设 AB=y,BC=x,求y关于x的函数表达式.
(2)(1)中的函数 y的值能否取8.5 请说明理由.
21.如图,一次函数y=x+1的图象交y轴于点A,与反比例函数 的图象相交于点B(m,2).求:
(1)反比例函数的表达式.
(2)△AOB的面积.
22.如图,点A 在第一象限内,AB⊥x轴于点 B,反比例函数 的图象分别交 AO,AB 于点C,D.已知点 C的坐标为(2,2),BD=1.
(1)求 k 的值及点 D 的坐标.
(2)已知点 P 在该反比例函数的图象上,且在△ABO的内部(包括边界),直接写出点 P 的横坐标x的取值范围.
23.如图,在同一平面直角坐标系中,一次函数y 和正比例函数 y =-2x的图象相交于点 A,反比例函数 的图象经过点 A.
(1)求反比例函数的表达式.
(2)写出当y >y 时,x的取值范围.
(3)设一次函数 的图象与反比例函数 的图象的另一个交点为 B,连结OB,求△ABO的面积.
24.如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点M,D分别在OA ,AB上,且AD=AM=2.一次函数y=kx+b的图象过点D和M,反比例函数y= 的图象经过点D,与BC交点为N.
(1)求反比例函数和一次函数的表达式;
(2)若点P在y轴上,且使四边形OMDP的面积与四边形OMNC的面积相等,求点P的坐标.
答案解析部分
1.【答案】D
2.【答案】D
3.【答案】D
4.【答案】D
5.【答案】D
6.【答案】D
7.【答案】C
8.【答案】A
9.【答案】B
10.【答案】C
11.【答案】p=
12.【答案】<
13.【答案】;
14.【答案】(-1,-6)
15.【答案】6
16.【答案】
17.【答案】12;9
18.【答案】240
19.【答案】(1)
(2)3
20.【答案】(1)
(2)不能.理由略
21.【答案】(1)
(2)
22.【答案】(1)解:∵反比例函数图象经过点C(2,2),
∴,解得k=4.
∴ 反比例函数解析式为.
又∵BD=1,∴点D 的纵坐标为1,
将y=1代入中,则x=4.
∴点D的坐标为(4,1).
∴k的值为4,点 D的坐标为(4,1).
(2)2≤x≤4.
23.【答案】(1)解:由题意可得,解得,
∴ 点A 的坐标为(-2,4).
将A(-2,4)代入中,可得k=-8,
∴ 反比例函数的表达式为.
(2)解:当y >y 时,正比例函数图象在反比例函数上方,
由题意可得,解得或,
∴ 两函数图象的交点横坐标为-2和-2,
∴当y >y 时,x的取值范围为-22.
(3)解:由题意可得,解得或,
∴ 点B的坐标为(-8,1).
设一次函数和x轴的交点为C,如图
则C的坐标为(-10,0),
∴ .
∴△ABO的面积15.
24.【答案】(1)解:∵C(0,3),∴OC=3.∵四边形OABC是正方形,∴OA=AB=3.∵AD=2,∴D(-3,2).∵点D在反比例函数y=的图象上,
∴m=-3×2=-6,∴反比例函数的表达式为y=
∵AM=2,
∴OM=OA-AM=1,∴M(-1,0).∵点D(-3,2),M(-1,0)在直线y=kx+b上,
∴解得
∴一次函数的表达式为y=-x-1.
(2)解:如图,过点D作DH⊥y轴于点H,连接MN,
由(1)知,反比例函数的表达式为y= ,
当y=3时,x= =-2,∴N( -2,3) , ∴S四边形OMNC= (CN+OM) ·OC= -×(2+1) ×3=4.5.设P(0,n),
∵四边形0MDP的面积与四边形OMNC的面积相等,
∴S四边形OMDP = (OM+DH) ·AD+ DH·PH= ×( 1+3)×2+ ×3×(n-2)=4.5,∴n= ,∴点P的坐标为(0,)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学人教版九年级下册第二十六章反比例函数重难点检测卷
一、选择题
1.函数 和y=-kx+2(k≠0); 在同一平面直角坐标系中的图象可能是 ( )
A. B.
C. D.
2.下列关于反比例函数 的说法,错误的是( )
A.图象经过点(1,-3) B.图象位于第二、四象限
C.图象关于直线y=x对称 D.y随x的增大而增大
3.某校科技小组进行野外考察,利用铺垫木板的方式,通过了一片湿泥地,他们发现:当人和木板对湿泥地的压力一定时,人和木板对地面的压强 p(Pa)随着木板面积S(m )的变化而变化,其关系式为 p 如果人和木板对湿泥地的压力 F 合计600 N,那么下列说法正确的是 ( )
A.p是S的正比例函数
B.当S越来越大时,p也越来越大
C.若压强不超过6000 Pa,则木板面积最大为 0.1m
D.当木板面积为0.2m 时,压强是3000 Pa
4. 某村耕地总面积为 50 公顷,且该村人均耕地面积y(公顷)与总人口x(人)的函数图象如图所示,则下列说法正确的是( )
A.该村人均耕地面积随总人口的增多而增多
B.该村人均耕地面积y与总人口x成正比例
C.若该村人均耕地面积为0.2公顷,则总人口为1000人
D.当该村总人口为50人时,人均耕地面积为1公顷
5.在同一平面直角坐标系中,一次函数+b与反比例函数(k k ≠0,x>0)的图象如图所示,则当 y >y 时,自变量x(x>0)的取值范围是( )
A.x<1 B.x>3 C.0
A.x>-2 B.-2
C.x>1 D.x<-2或0
A.7分钟 B.8分钟 C.9分钟 D.10分钟
8.如图,平面直角坐标系中,O是坐标原点,点A是反比例函数y=(k≠0)图象上的一点,过点A分别作AM⊥x轴于点M ,AN⊥y轴于点N,若四边形AMON的面积为2,则k的值是.( )
A.2 B.-2 C.1 D.-1
9.如图,过点C(1,0)作两条直线,分别交函数y=(x>0),y=(x<0)的图象于A,B两点,连结AB.若AB∥x轴,则△ABC的面积是( )
A.2 B.3 C.4 D.6
10.在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
A.( ,0) B.(2,0)
C.( ,0) D.(3,0)
二、填空题
11. 当温度不变时,气球内气体的压强 p(kPa)是气体体积V(m )的函数,下表记录了一组实验数据:
V(m ) 1 1.5 2 2.5 3
p(kPa) 96 64 48 38.4 32
p关于V的函数表达式可能是 。
12.若点(2,m),(2,n)分别在反比例函数和 的图象上,则 m 和 n 的大小关系是m n(填“>”“<”或“=”).
13.已知点 A(-2,m)在一个反比例函数的图象上,点 A'与点 A 关于 y轴对称.若点 A'在正比例函数的图象上,则这个反比例函数的表达式为 .当x>2时,反比例函数值 y的取值范围是 .
14.如图, 已知点A(2,3),B(0,2),点 A 在反比例函数 的图象上,作射线 AB,再将射线 AB绕点 A 按逆时针方向旋转 45°,交反比例函数的图象于点 C,则点 C 的坐标为 .
15.如图,在平面直角坐标系xOy中,点A(0,4),B(3,4) ,将△ABO向右平移到△CDE的位置,A的对应点是C,0的对应点是E,函数y= (k≠0)的图象经过点C和DE的中点F,则k的值是
16.如图,在平面直角坐标系中,直线y1=k1x+b与双曲线y2=(其中k1,k2≠0)相交于A(-2,3),B(m,-2)两点,过点B作BP∥x轴,交y轴于点P,则△ABP的面积是
17.如图,点A,B分别在函数y= (a>0)图象的两支上(点A在第一象限),连结AB交x轴于点C.点D,E在函数y= (b<0,x<0)图象上,AE∥x轴,BD∥y轴,连结DE,BE.若点A到x轴的距离是点B的2倍,△ABE的面积为9,四边形ABDE的面积为14,则a-b的值 ,a的值为
18.列车从甲地驶往乙地.行完全程所需的时间与行驶的平均速度之间的反比例函数关系如图所示.若列车要在内到达,则速度至少需要提高到 .
三、解答题
19.已知y是x的反比例函数,且当x=2时,y=6.
(1)求y关于x的函数表达式.
(2)当x=4时,求y的值.
20.如图,老李想利用一段5m 长的墙(图中 EF),建一个面积为32 m 的矩形猪圈,另外三面(图中 AB,BC,CD)需要自己修建.老李准备了可以修建20 m墙的材料(可以不用完).
(1)设 AB=y,BC=x,求y关于x的函数表达式.
(2)(1)中的函数 y的值能否取8.5 请说明理由.
21.如图,一次函数y=x+1的图象交y轴于点A,与反比例函数 的图象相交于点B(m,2).求:
(1)反比例函数的表达式.
(2)△AOB的面积.
22.如图,点A 在第一象限内,AB⊥x轴于点 B,反比例函数 的图象分别交 AO,AB 于点C,D.已知点 C的坐标为(2,2),BD=1.
(1)求 k 的值及点 D 的坐标.
(2)已知点 P 在该反比例函数的图象上,且在△ABO的内部(包括边界),直接写出点 P 的横坐标x的取值范围.
23.如图,在同一平面直角坐标系中,一次函数y 和正比例函数 y =-2x的图象相交于点 A,反比例函数 的图象经过点 A.
(1)求反比例函数的表达式.
(2)写出当y >y 时,x的取值范围.
(3)设一次函数 的图象与反比例函数 的图象的另一个交点为 B,连结OB,求△ABO的面积.
24.如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点M,D分别在OA ,AB上,且AD=AM=2.一次函数y=kx+b的图象过点D和M,反比例函数y= 的图象经过点D,与BC交点为N.
(1)求反比例函数和一次函数的表达式;
(2)若点P在y轴上,且使四边形OMDP的面积与四边形OMNC的面积相等,求点P的坐标.
答案解析部分
1.【答案】D
2.【答案】D
3.【答案】D
4.【答案】D
5.【答案】D
6.【答案】D
7.【答案】C
8.【答案】A
9.【答案】B
10.【答案】C
11.【答案】p=
12.【答案】<
13.【答案】;
14.【答案】(-1,-6)
15.【答案】6
16.【答案】
17.【答案】12;9
18.【答案】240
19.【答案】(1)
(2)3
20.【答案】(1)
(2)不能.理由略
21.【答案】(1)
(2)
22.【答案】(1)解:∵反比例函数图象经过点C(2,2),
∴,解得k=4.
∴ 反比例函数解析式为.
又∵BD=1,∴点D 的纵坐标为1,
将y=1代入中,则x=4.
∴点D的坐标为(4,1).
∴k的值为4,点 D的坐标为(4,1).
(2)2≤x≤4.
23.【答案】(1)解:由题意可得,解得,
∴ 点A 的坐标为(-2,4).
将A(-2,4)代入中,可得k=-8,
∴ 反比例函数的表达式为.
(2)解:当y >y 时,正比例函数图象在反比例函数上方,
由题意可得,解得或,
∴ 两函数图象的交点横坐标为-2和-2,
∴当y >y 时,x的取值范围为-2
(3)解:由题意可得,解得或,
∴ 点B的坐标为(-8,1).
设一次函数和x轴的交点为C,如图
则C的坐标为(-10,0),
∴ .
∴△ABO的面积15.
24.【答案】(1)解:∵C(0,3),∴OC=3.∵四边形OABC是正方形,∴OA=AB=3.∵AD=2,∴D(-3,2).∵点D在反比例函数y=的图象上,
∴m=-3×2=-6,∴反比例函数的表达式为y=
∵AM=2,
∴OM=OA-AM=1,∴M(-1,0).∵点D(-3,2),M(-1,0)在直线y=kx+b上,
∴解得
∴一次函数的表达式为y=-x-1.
(2)解:如图,过点D作DH⊥y轴于点H,连接MN,
由(1)知,反比例函数的表达式为y= ,
当y=3时,x= =-2,∴N( -2,3) , ∴S四边形OMNC= (CN+OM) ·OC= -×(2+1) ×3=4.5.设P(0,n),
∵四边形0MDP的面积与四边形OMNC的面积相等,
∴S四边形OMDP = (OM+DH) ·AD+ DH·PH= ×( 1+3)×2+ ×3×(n-2)=4.5,∴n= ,∴点P的坐标为(0,)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
