2023-2024学年第二学期甘肃省武威第十七中学教研联片九年级数学开学学情评估(含答案)
文档属性
| 名称 | 2023-2024学年第二学期甘肃省武威第十七中学教研联片九年级数学开学学情评估(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 220.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-12 23:49:35 | ||
图片预览


文档简介
2023-2024学年第二学期甘肃省武威第十七中学教研联片
九年级数学开学学情评估
一、选择题(共30分)
1.(3分)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.(3分) 已知直角三角形的两条直角边长恰好是方程的两个根,则此直角三角形斜边长是( )
A.13 B.5 C. D.
3.(3分) 已知一元二次方程的两根分别为,,则的值为( )
A. B. C. D.
4.(3分)要组织一次排球邀请赛,参赛的每个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛.设比赛组织者应邀请x个队参赛,则x满足的关系式为( )
A. B.
C. D.
5.(3分)已知二次函数y=ax2+bx+c的图象如图所示,下列说法错误的是( )
A.图象关于直线x=1对称
B.函数y=ax2+bx+c的最小值是-4
C.当-4≤x≤3时,y≥0
D.当x<1时,y随x的增大而减小
6.(3分)抛物线与抛物线的相同点是( )
A.顶点相同 B.对称轴相同
C.抛物线形状相同 D.顶点都在轴上
7.(3分)如图,在中,,将绕点逆时针旋转到的位置,使得,则的度数是( )
A. B. C. D.
8.(3分)在平面直角坐标系中,点关于原点对称的点的坐标是( )
A. B. C. D.
9.(3分)如图,已知⊙O的直径CD=8,AB是⊙O的弦,AB⊥CD,垂足为M,OM=2,则AB的长为( )
A.2 B. C.4 D.
10.(3分)在一个不透明的袋子中放入15个红球和若干个白球(球除了颜色不同外其余都相同),如果从袋子里摸出一个球记录下颜色后放回,经过多次重复试验后,发现摸到红球的频率稳定在0.6,则袋中白球有( )
A.5个 B.10个 C.15个 D.25个
二、填空题(共24分)
11.(3分)关于的方程的一个根为,那么的值是 .
12.(3分)若关于x的方程(m+2)x|m|+2x-3=0是一元二次方程,则m= .
13.(3分)抛物线 的顶点坐标是 .
14.(3分)抛物线可以由抛物线向 平移个单位得到.
15.(3分)如图,将绕点逆时针旋转,得到,若点恰好在的延长线上,则的度数为 .
16.(3分)在平面直角坐标系中,将点绕原点逆时针旋转180°得到点,则点的坐标是 ;
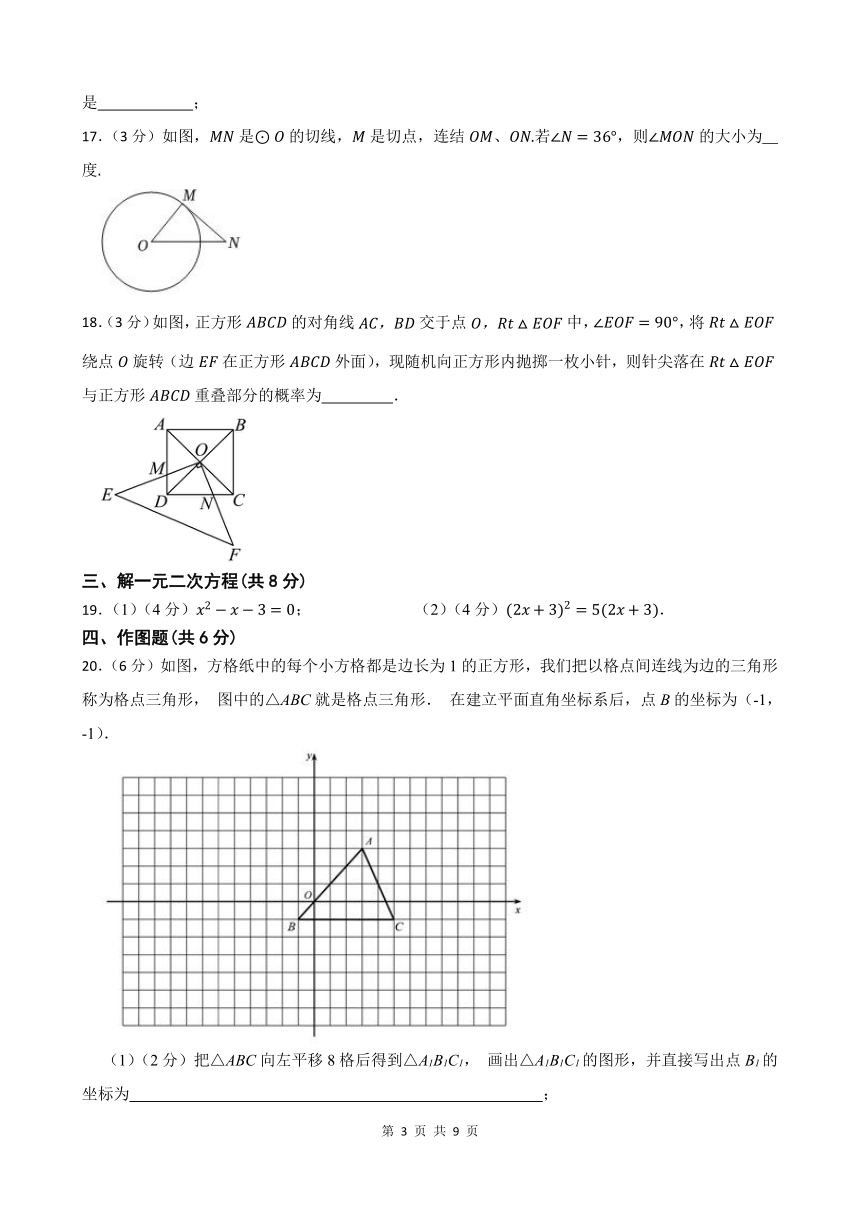
17.(3分)如图,是的切线,是切点,连结、若,则的大小为 度
18.(3分)如图,正方形的对角线交于点中,,将绕点旋转(边在正方形外面),现随机向正方形内抛掷一枚小针,则针尖落在与正方形重叠部分的概率为 .
三、解一元二次方程(共8分)
19.(1)(4分); (2)(4分).
四、作图题(共6分)
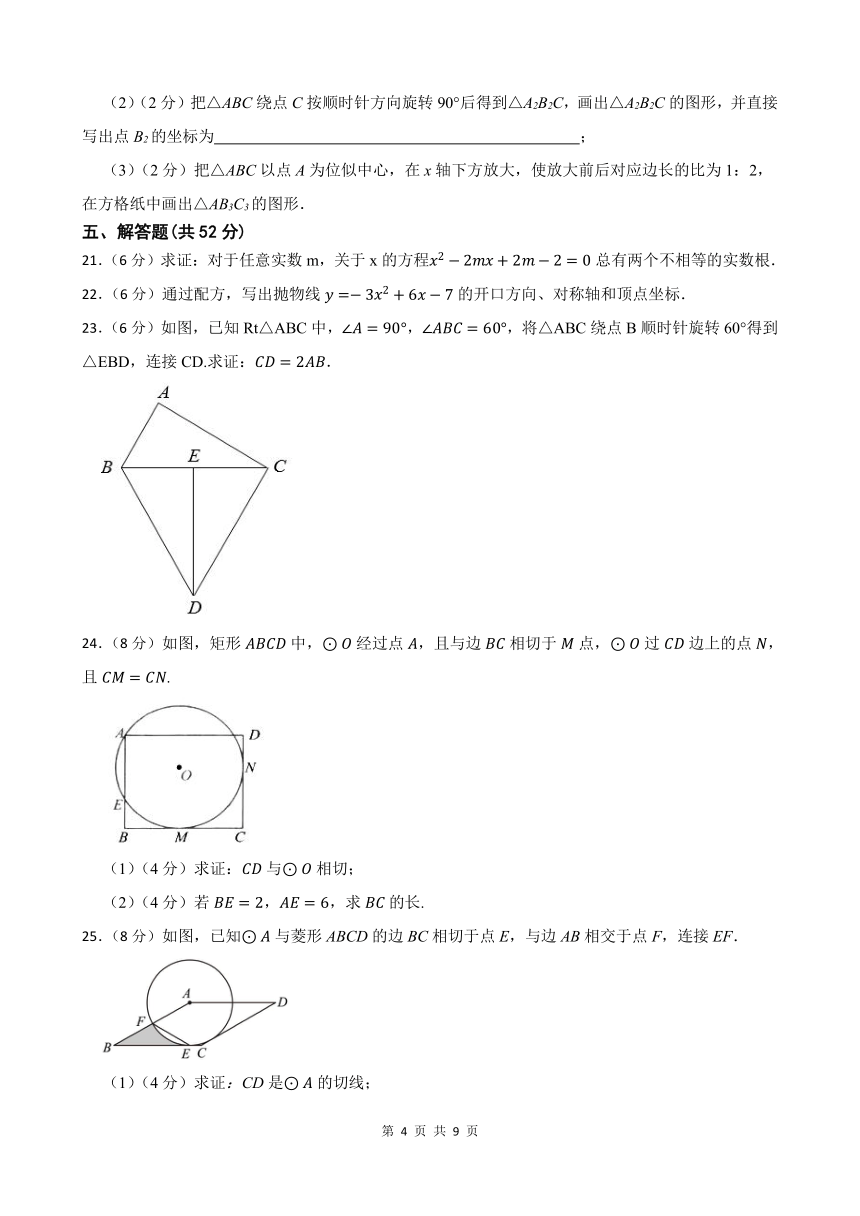
20.(6分)如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为格点三角形, 图中的△ABC就是格点三角形. 在建立平面直角坐标系后,点B的坐标为(-1,-1).
(1)(2分)把△ABC向左平移8格后得到△A1B1C1, 画出△A1B1C1的图形,并直接写出点B1的坐标为 ;
(2)(2分)把△ABC绕点C按顺时针方向旋转90°后得到△A2B2C,画出△A2B2C的图形,并直接写出点B2的坐标为 ;
(3)(2分)把△ABC以点A为位似中心,在x轴下方放大,使放大前后对应边长的比为1:2,在方格纸中画出△AB3C3的图形.
五、解答题(共52分)
21.(6分)求证:对于任意实数m,关于x的方程总有两个不相等的实数根.
22.(6分)通过配方,写出抛物线的开口方向、对称轴和顶点坐标.
23.(6分)如图,已知Rt△ABC中,,,将△ABC绕点B顺时针旋转60°得到△EBD,连接CD.求证:.
24.(8分)如图,矩形中,经过点,且与边相切于点,过边上的点,且.
(1)(4分)求证:与相切;
(2)(4分)若,,求的长.
25.(8分)如图,已知与菱形ABCD的边BC相切于点E,与边AB相交于点F,连接EF.
(1)(4分)求证:CD是的切线;
(2)(4分)若的半径为2,,求图中阴影部分的面积.
26.(8分)在一个不透明的盒子里有红球、黄球、绿球各一个,它们除了颜色外其余都相同,小颖从盒子里随机摸出一球,记录下颜色后放回盒子里,充分摇匀后,再随机摸出一球,并记录下颜色.请用列表法或画树状图法,求小颖两次摸出的球颜色相同的概率.
27.(10分)已知二次函数 ( 是常数).
(1)(3分)求证:不论 为何值,该函数的图象与 轴有 个公共点;
(2)(3分)如图,若该函数与 轴的一交点是原点,求另一交点 的坐标及顶点 的坐标;
(3)(4分)在(2)的条件下, 轴上是否存在一点 ,使得 最小?若存在,求出点 的坐标;若不存在,请说明理由.
答案
1-10 CDABC DBADB
11. 12.2 13.(2,1) 14.下 15. 16. 17.54 18.
19.(1)解:,
这里,,,
,
,
,;
(2)解:,
,
,
或,
,.
20.略
21.证明:
∵,
∴.
∴对于任意实数m,关于x的方程总有两个不相等的实数根.
22.解:,
∵,
∴抛物线的开口向下,
对称轴为直线,顶点坐标为
23.证明:在Rt△ABC中,,,
∴,
∴.
∵△ABC绕点B顺时针旋转60°得到△EBD,
∴,,
∴△CBD是等边三角形,
∴.
24.(1)证明:连接,,,
,,,,
与相切于,,,
,,
又是的半径,与相切;
(2)解:过点作于,连接,
,,
四边形是矩形,,
又,四边形是矩形,
,,
,,
,,,
四边形是矩形,,
25.(1)证明:连接AE,作AH⊥CD于H,
∵BC切⊙A于点E,∴AE⊥BC ,
∴∠AEB=∠AHD=90°,
在菱形ABCD中,AB=AD,∠B=∠D,
∴△ABE≌△ADH ∴AH=AE,
又∵AE是半径,AH⊥CD ,
∴CD是⊙A的切线;
(2)解:∵∠BEF=30°,由(1)知∠AEB=90°,
∴∠AEF=60°,
∵AE=AF, ∴ △AFE是等边三角形,∴∠FAE=60°,∠B=30°,
又∵AE=2 , AB=2AE=4,∴,
∴ ,
又∵,
∴;
26.解:画树状图如下:
共有9种等可能的结果,小颖两次摸出的球颜色相同的结果有3个,
小颖两次摸出的球颜色相同的概率为.
27.(1)证明:令 ,即 ,
∴ , , ,
∴ ,
∴ ,
∴不论 为何值,该函数的图象 轴有2个公共点;
(2)解:已知函数 过 ,
∴ ,
解得: ,
∴ ,
当 时, ,
解得: , ,
∴ ,
由 可得 ,
∴ ;
(3)存在.
解:如图所示作 关于 轴的对称点 ,
设直线 : ,且 , ,
∴ ,
解得: ,
∴ ,
当 时, ,
.
九年级数学开学学情评估
一、选择题(共30分)
1.(3分)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.(3分) 已知直角三角形的两条直角边长恰好是方程的两个根,则此直角三角形斜边长是( )
A.13 B.5 C. D.
3.(3分) 已知一元二次方程的两根分别为,,则的值为( )
A. B. C. D.
4.(3分)要组织一次排球邀请赛,参赛的每个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛.设比赛组织者应邀请x个队参赛,则x满足的关系式为( )
A. B.
C. D.
5.(3分)已知二次函数y=ax2+bx+c的图象如图所示,下列说法错误的是( )
A.图象关于直线x=1对称
B.函数y=ax2+bx+c的最小值是-4
C.当-4≤x≤3时,y≥0
D.当x<1时,y随x的增大而减小
6.(3分)抛物线与抛物线的相同点是( )
A.顶点相同 B.对称轴相同
C.抛物线形状相同 D.顶点都在轴上
7.(3分)如图,在中,,将绕点逆时针旋转到的位置,使得,则的度数是( )
A. B. C. D.
8.(3分)在平面直角坐标系中,点关于原点对称的点的坐标是( )
A. B. C. D.
9.(3分)如图,已知⊙O的直径CD=8,AB是⊙O的弦,AB⊥CD,垂足为M,OM=2,则AB的长为( )
A.2 B. C.4 D.
10.(3分)在一个不透明的袋子中放入15个红球和若干个白球(球除了颜色不同外其余都相同),如果从袋子里摸出一个球记录下颜色后放回,经过多次重复试验后,发现摸到红球的频率稳定在0.6,则袋中白球有( )
A.5个 B.10个 C.15个 D.25个
二、填空题(共24分)
11.(3分)关于的方程的一个根为,那么的值是 .
12.(3分)若关于x的方程(m+2)x|m|+2x-3=0是一元二次方程,则m= .
13.(3分)抛物线 的顶点坐标是 .
14.(3分)抛物线可以由抛物线向 平移个单位得到.
15.(3分)如图,将绕点逆时针旋转,得到,若点恰好在的延长线上,则的度数为 .
16.(3分)在平面直角坐标系中,将点绕原点逆时针旋转180°得到点,则点的坐标是 ;
17.(3分)如图,是的切线,是切点,连结、若,则的大小为 度
18.(3分)如图,正方形的对角线交于点中,,将绕点旋转(边在正方形外面),现随机向正方形内抛掷一枚小针,则针尖落在与正方形重叠部分的概率为 .
三、解一元二次方程(共8分)
19.(1)(4分); (2)(4分).
四、作图题(共6分)
20.(6分)如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为格点三角形, 图中的△ABC就是格点三角形. 在建立平面直角坐标系后,点B的坐标为(-1,-1).
(1)(2分)把△ABC向左平移8格后得到△A1B1C1, 画出△A1B1C1的图形,并直接写出点B1的坐标为 ;
(2)(2分)把△ABC绕点C按顺时针方向旋转90°后得到△A2B2C,画出△A2B2C的图形,并直接写出点B2的坐标为 ;
(3)(2分)把△ABC以点A为位似中心,在x轴下方放大,使放大前后对应边长的比为1:2,在方格纸中画出△AB3C3的图形.
五、解答题(共52分)
21.(6分)求证:对于任意实数m,关于x的方程总有两个不相等的实数根.
22.(6分)通过配方,写出抛物线的开口方向、对称轴和顶点坐标.
23.(6分)如图,已知Rt△ABC中,,,将△ABC绕点B顺时针旋转60°得到△EBD,连接CD.求证:.
24.(8分)如图,矩形中,经过点,且与边相切于点,过边上的点,且.
(1)(4分)求证:与相切;
(2)(4分)若,,求的长.
25.(8分)如图,已知与菱形ABCD的边BC相切于点E,与边AB相交于点F,连接EF.
(1)(4分)求证:CD是的切线;
(2)(4分)若的半径为2,,求图中阴影部分的面积.
26.(8分)在一个不透明的盒子里有红球、黄球、绿球各一个,它们除了颜色外其余都相同,小颖从盒子里随机摸出一球,记录下颜色后放回盒子里,充分摇匀后,再随机摸出一球,并记录下颜色.请用列表法或画树状图法,求小颖两次摸出的球颜色相同的概率.
27.(10分)已知二次函数 ( 是常数).
(1)(3分)求证:不论 为何值,该函数的图象与 轴有 个公共点;
(2)(3分)如图,若该函数与 轴的一交点是原点,求另一交点 的坐标及顶点 的坐标;
(3)(4分)在(2)的条件下, 轴上是否存在一点 ,使得 最小?若存在,求出点 的坐标;若不存在,请说明理由.
答案
1-10 CDABC DBADB
11. 12.2 13.(2,1) 14.下 15. 16. 17.54 18.
19.(1)解:,
这里,,,
,
,
,;
(2)解:,
,
,
或,
,.
20.略
21.证明:
∵,
∴.
∴对于任意实数m,关于x的方程总有两个不相等的实数根.
22.解:,
∵,
∴抛物线的开口向下,
对称轴为直线,顶点坐标为
23.证明:在Rt△ABC中,,,
∴,
∴.
∵△ABC绕点B顺时针旋转60°得到△EBD,
∴,,
∴△CBD是等边三角形,
∴.
24.(1)证明:连接,,,
,,,,
与相切于,,,
,,
又是的半径,与相切;
(2)解:过点作于,连接,
,,
四边形是矩形,,
又,四边形是矩形,
,,
,,
,,,
四边形是矩形,,
25.(1)证明:连接AE,作AH⊥CD于H,
∵BC切⊙A于点E,∴AE⊥BC ,
∴∠AEB=∠AHD=90°,
在菱形ABCD中,AB=AD,∠B=∠D,
∴△ABE≌△ADH ∴AH=AE,
又∵AE是半径,AH⊥CD ,
∴CD是⊙A的切线;
(2)解:∵∠BEF=30°,由(1)知∠AEB=90°,
∴∠AEF=60°,
∵AE=AF, ∴ △AFE是等边三角形,∴∠FAE=60°,∠B=30°,
又∵AE=2 , AB=2AE=4,∴,
∴ ,
又∵,
∴;
26.解:画树状图如下:
共有9种等可能的结果,小颖两次摸出的球颜色相同的结果有3个,
小颖两次摸出的球颜色相同的概率为.
27.(1)证明:令 ,即 ,
∴ , , ,
∴ ,
∴ ,
∴不论 为何值,该函数的图象 轴有2个公共点;
(2)解:已知函数 过 ,
∴ ,
解得: ,
∴ ,
当 时, ,
解得: , ,
∴ ,
由 可得 ,
∴ ;
(3)存在.
解:如图所示作 关于 轴的对称点 ,
设直线 : ,且 , ,
∴ ,
解得: ,
∴ ,
当 时, ,
.
同课章节目录
