比例应用题易错汇编(含答案)数学六年级下册北师大版
文档属性
| 名称 | 比例应用题易错汇编(含答案)数学六年级下册北师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 774.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-13 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
比例应用题易错汇编-数学六年级下册北师大版
1.一幅中国交通地图比例尺为在这幅地图上量得甲、乙两座城市之间相距6厘米,一辆出租车从甲城开出,3.75小时后到达乙城。出租车平均每小时行多少千米?
2.看图填一填,画一画。
(1)新华书店到学校的实际距离是( )米。
(2)小月家在学校北偏东45°方向,实际距离为900米的地方,请在图中标出小月家的位置。
3.某核酸检测点进行了为期三天的核酸检测,第一天有450人进行了核酸检测,第二天进行核酸检测的人数比第一天多,第三天与第二天进行核酸检酬的人数比是,该检测点第三天有多少人进行了核酸检测?(用比例解答)
4.一个机器实际零件长5毫米,画在比例尺是的图纸上,应画多少厘米?
5.如图,已知小红家到体育场的实际距离是7.5km。
(1)这幅图的比例尺是多少?
(2)从小红家到游乐园,实际要走多少千米?
(3)已知博物馆在游乐园的西偏北方向,实际距离为10km的地方,请在图中标出博物馆的位置。
6.将一个长25米,宽15米的长方形按1∶500的比例尺画在图纸上,该长方形在图纸上的面积是多少平方厘米?
7.某社区在封控时招募了216名志愿者,其中女性占,后来又来了若干名女性志愿者,使女性志愿者与男性志愿者的人数之比是3∶7,后来又来了多少名女性志愿者?(用比例解)
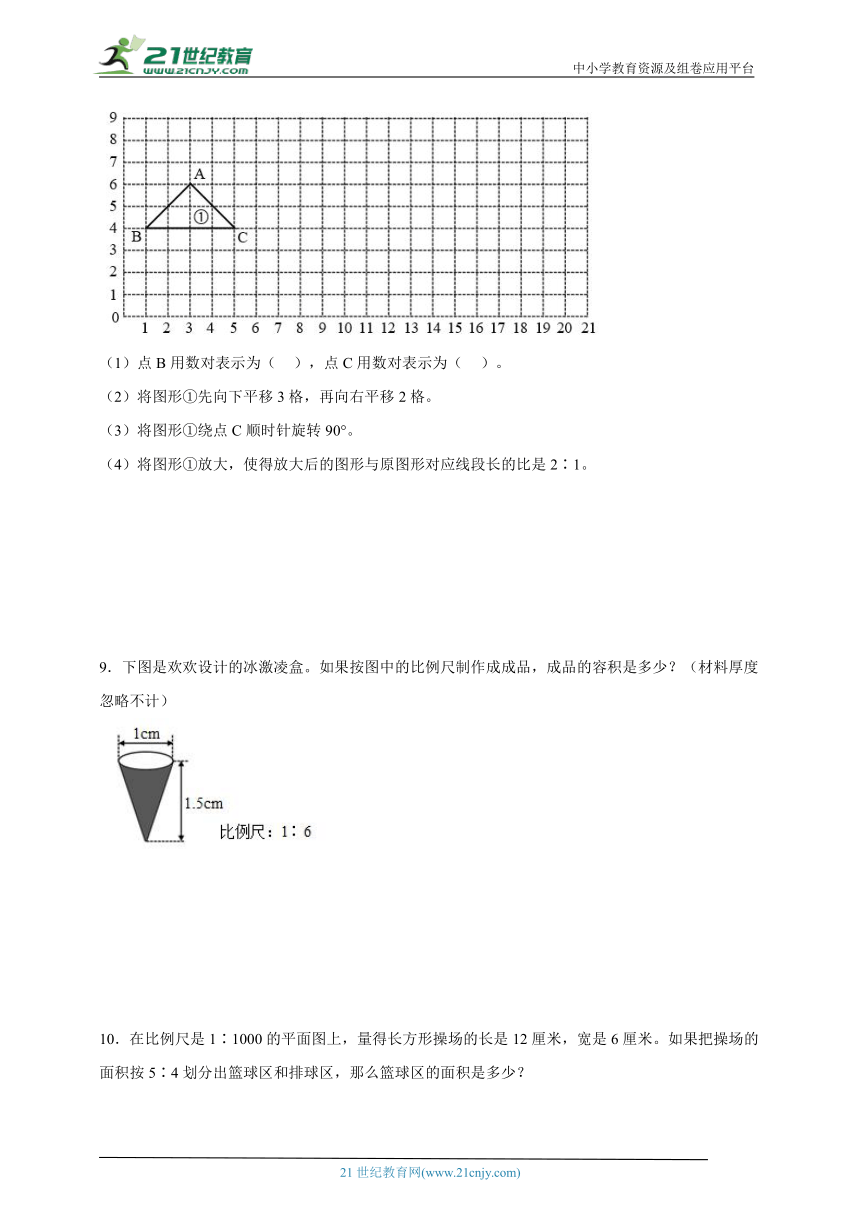
8.已知点A用数对表示为(3,6),按要求填一填,画一画。
(1)点B用数对表示为( ),点C用数对表示为( )。
(2)将图形①先向下平移3格,再向右平移2格。
(3)将图形①绕点C顺时针旋转90°。
(4)将图形①放大,使得放大后的图形与原图形对应线段长的比是2∶1。
9.下图是欢欢设计的冰激凌盒。如果按图中的比例尺制作成成品,成品的容积是多少?(材料厚度忽略不计)
10.在比例尺是1∶1000的平面图上,量得长方形操场的长是12厘米,宽是6厘米。如果把操场的面积按5∶4划分出篮球区和排球区,那么篮球区的面积是多少?
11.希望小学装修多媒体教室,计划用边长4分米的方砖铺地。需要800块。实际用边长8分米的正方形大理石铺地,则需要多少块正方形大理石?
12.“中国天眼”是目前全球最大的球面射电望远镜(简称FAST),它的球面口为圆,口径500米,与美国阿雷西博(Arecibo)305米口径望远镜相比,其综合性能提高约10倍。FAST将在未来20年保持世界一流设备的地位,成为世界天文学研究的“利器”。
(1)我国FAST球面口的面积是多少平方米?
(2)我国FAST与美国Arecibo球面口周长的最简比是( )。
(3)我国科学家在设计FAST时,设计图纸上的球面口直径是50cm,这幅设计图的比例尺是( )。
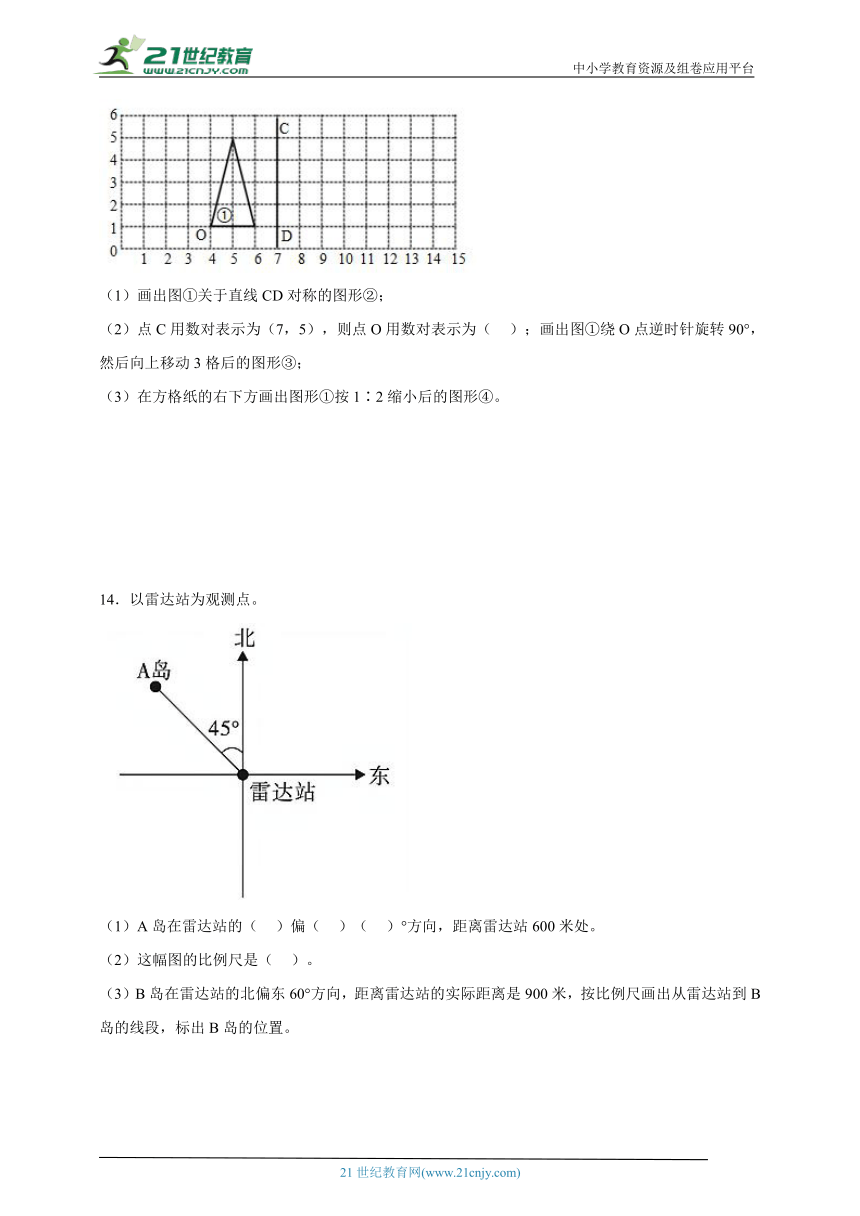
13.填一填、画一画(下面每个小正方形的边长表示1厘米)。
(1)画出图①关于直线CD对称的图形②;
(2)点C用数对表示为(7,5),则点O用数对表示为( );画出图①绕O点逆时针旋转90°,然后向上移动3格后的图形③;
(3)在方格纸的右下方画出图形①按1∶2缩小后的图形④。
14.以雷达站为观测点。
(1)A岛在雷达站的( )偏( )( )°方向,距离雷达站600米处。
(2)这幅图的比例尺是( )。
(3)B岛在雷达站的北偏东60°方向,距离雷达站的实际距离是900米,按比例尺画出从雷达站到B岛的线段,标出B岛的位置。
15.在一幅比例尺为1∶50000的地图上,欢欢发现某公园的占地接近于一个长方形。她用直尺量得这个长方形的长为2.4cm,宽为1.8cm。请你根据以上信息测算出该公园的占地面积约多少公顷?
16.在一幅比例尺是1∶15000000的地图上,A地到B地的图上距离是5厘米,甲、乙两车同时从A,B两地相向而行,甲车每小时行66千米,5小时后两车相遇,乙车每小时行多少千米?
17.甲,乙两个车间原来人数比为7∶3,甲车间人数调出后,还剩42人,乙车间原来有多少人?(用比例解)
18.按要求填一填,画一画。
(1)点A的位置用数对表示,点B的位置用数对( )表示,点C的位置用数对( )表示。
(2)以虚线为对称轴,画出图形①的轴对称图形。
(3)将图形①先向左平移6格,再向下平移2格。
(4)将图形②绕点A逆时针旋转90度。
(5)将图形③缩小,使得缩小后的图形与原图形对应线段长的比是。
19.下面是小明家位置图,按要求回答:
(1)奶奶生病了,请你用文字描述奶奶从小明家去医院看病所走的线路。
(2)看完病,奶奶有点饿了,想在医院的正西方向距医院200米的饭店就餐,请在图中用★标出饭店的位置并写出计算过程。
20.兄弟两人月收入的比为4∶3,月支出比为11∶6,月结余均为3600元,问每人每月收入多少元?
21.请按要求完成:
(1)将图中A点、C点的位置分别用数对表示出来:( )、( )。
(2)画出这个三角形绕B点顺时针旋转90°后的图形。
(3)按2∶1画出这个三角形放大后的图形,放大后的图形与原三角形面积比是( )。
(4)从图中可知,A点在C点的( )偏( )( )°方向。
参考答案:
1.80千米
【分析】根据实际距离=图上距离÷比例尺,代入数据,求出甲、乙两座城市之间的实际距离,再根据速度=路程÷时间,代入数据,即可解答。
【详解】6÷
=6×5000000
=30000000(厘米)
30000000厘米=300(千米)
300÷3.75=80(千米)
答:出租车平均每小时行80千米。
【点睛】本题考查实际距离和图上距离的换算,以及根据速度、时间和路程三者的关系解答问题,注意单位名数之间的换算。
2.(1)600
(2)见详解
【分析】(1)通过测量,新华书店到学校的图上距离是2厘米;根据实际距离=图上距离÷比例尺,代入数据,求出新华书店到学校的实际距离;
(2)根据地图上方向的规定:上北下南,左西右东;以学校的位置为观测点,即可确定小月家方向,再根据学校与小月家的实际距离以及图中所标注的比例尺,求出学校与小月家的图上距离,从而在图中标出小月家的位置。
【详解】(1)量得新华书店到学校的图上距离是2厘米。
2÷
=2×30000
=60000(厘米)
60000厘米=600米
新华书店到学校的实际距离是600米。
(2)900米=90000厘米
90000×=3(厘米)
【点睛】本题利用方向和距离在平面图中确定物体位置的方法以及比例尺的灵活应用,画平面图的关键一是方向的确定,二是根据实际距离以及比例尺求出图上距离。
3.660人
【分析】把第一天进行核酸检测的人数看作单位“1”,第二天进行核酸检测的人数是第一天的(1+),用第一天核酸检测人数×(1+),求出第二天核酸检测人数;
设该核酸检查点第三天核酸检测人数是x人,根据第三天与第二天进行核酸检测的人数比是11∶9,列比例:x∶第二天核酸检测人数=11∶9,解比例,即可解答。
【详解】450×(1+)
=450×
=540(人)
解:设该核酸检查点第三天有x人进行核酸检测。
x∶540=11∶9
9x=540×11
9x=5940
x=5940÷9
x=660
答:该核酸检测点第三天有660人进行了核酸检测。
【点睛】本题先根据分数乘法的意义,求出第二天核酸检测的人数,再根据比例的基本性质,求出第三天核酸检测的人数。
4.4厘米
【分析】图上距离=实际距离×比例尺,代入数据,即可解答。
【详解】5毫米=0.5厘米
0.5×8=4(厘米)
答:应画4厘米。
【点睛】本题考查实际距离和图上距离之间的换算,注意单位名数的统一。
5.(1)1∶500000
(2)35千米
(3)见详解
【分析】(1)根据小红家到体育场的实际距离,再量出小红家到体育场的图上距离,根据比例尺的意义:比例尺=图上距离∶实际距离,求出这幅图的比例尺;
(2)量出小红家到游乐园的图上距离;再根据实际距离=图上距离÷比例尺,求出这幅图小红家到游乐园的实际距离;
(3)根据图上距离=实际距离×比例尺,代入数据,求出游乐园到博物馆的图上距离;再以游乐园为观测点,根据方向,角度和距离,画出博物馆的位置。
【详解】(1)量出小红家到体育场的图上距离是1.5厘米。
7.5千米=750000厘米
1.5∶750000
=(1.5÷1.5)∶(750000÷1.5)
=1∶500000
答:这幅图的比例尺是1∶500000。
(2)量出小红家到游乐园的图上距离是7厘米。
7÷
=7×500000
=3500000(厘米)
3500000厘米=35千米
答:从小红家到游乐园,实际要走35千米。
(3)10千米=1000000厘米
1000000×=2(厘米)
【点睛】本题考查比例尺的意义,图上距离和实际距离之间的换算,以及根据方向、角度和距离确定物体位置。
6.15平方厘米
【分析】实际距离和比例尺已知,根据“图上距离=实际距离×比例尺”即可分别求出长方形的长和宽的图上距离,利用长方形的面积S=ab即可求出它的图上面积。
【详解】25米=2500厘米
15米=1500厘米
2500×=5(厘米)
1500×=3(厘米)
5×3=15(平方厘米)
答:该长方形在图纸上的面积是15平方厘米。
【点睛】此题主要考查图上距离、实际距离和比例尺的关系以及长方形的面积的计算方法,解答时要注意单位的换算。
7.24名
【分析】根据原来女性占总人数的分率,求出女性和男性的人数,再设后来来了x名女性,根据女性和男性人数比,列比例求解。
【详解】原来女性人数:216×=48(名)
男性人数:216-48=168(名)
解:设后来来了x名女性。
(48+x)∶168=3∶7
7×(48+x)=3×168
336+7x=504
336+7x-336=504-336
7x=168
7x÷7=168÷7
x=24
答:后来又来了24名女性志愿者。
【点睛】本题主要考查比例的应用,关键注意男性志愿者的人数没有改变。
8.(1)B(1,4);C(5,4)
(2)(3)(4)见详解
【分析】(1)根据数对的表示方法:第一个数字表示列,第二个数字表示行,由此即可用数对表示出点B和点C。
(2)根据平移的特征,把图形①各顶点分别向下平移3格,再向右平移2格,依次连结即可得到向下平移3格,再向右平移2格后的图形。
(3)根据旋转的特征,图形①绕点C顺时针旋转90°,点C的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(4)按2∶1把图形①放大,则放大后的图形各边的长度是图形①的2倍。
【详解】(1)B(1,4);C(5,4)
(2)(3)(4)如下图所示:
【点睛】本题考查的知识点比较多,要熟练掌握图形的旋转,平移的画法以及图形的放大和用数对表示位置的方法并灵活运用。
9.84.78立方厘米
【分析】根据实际距离=图上距离÷比例尺,代入数据,取出冰激凌的底面直径和高的实际长度,再根据圆锥体的体积公式:体积=底面积×高×,代入数据,即可解答。
【详解】冰激凌的底面直径:
1÷
=1×6
=6(厘米)
冰激凌的高:
1.5÷
=1.5×6
=9(厘米)
3.14×(6÷2)2×9×
=3.14×9×9×
=28.26×9×
=254.34×
=84.78(立方厘米)
答:成品的容积是84.78立方厘米。
【点睛】利用实际距离和图上距离之间的换算,以及圆锥的体积公式进行解答。
10.4000平方米
【分析】根据“图上距离÷比例尺=实际距离”,代入数值分别计算出操场实际的长和宽,然后根据“长方形的面积=长×宽”,代入数值计算可求得操场的实际面积,由于这个操场按5∶4划出篮球区和排球区,所以篮球区的面积是操场实际面积的,用操场实际面积乘就是篮球区的面积;据此解答。
【详解】12÷=12000(厘米)
12000厘米=120米
6÷=6000(厘米)
6000厘米=60米
60×120=7200(平方米)
7200×
=7200×
=4000(平方米)
答:篮球区的面积是4000平方米。
【点睛】解答此题用到的知识点:(1)图上距离、实际距离和比例尺三者之间的关系;(2)长方形的面积计算方法。
11.200块
【分析】多媒体教室的面积不变,所以所需方砖的块数×每块方砖的面积=多媒体教室的面积(一定),乘积一定,所以所需方砖的块数和每块方砖的面积成反比例关系,据此设出未知数,列比例解答即可。
【详解】解:设用边长8分米的正方形大理石铺地,则需要x块正方形大理石。
4×4×800=8×8x
64x=12800
64x÷64=12800÷64
x=200
答:用边长8分米的正方形大理石铺地,则需要200块正方形大理石。
【点睛】明确题中所需方砖的块数和每块方砖的面积成反比例关系是解题的关键。
12.(1)196250平方米
(2)100∶61
(3)1∶1000
【分析】(1)根据圆的面积公式:面积=π×半径2;代入数据,求出面积;
(2)根据圆的周长公式:周长=π×直径;代入数据,分别求出我国FAST和美国Arecibo球面口周长,再根据比的意义,进行解答;
(3)根据比例尺的意义:比例尺=图上距离∶实际距离,代入数据,求出这幅设计的比例尺。
【详解】(1)3.14×(500÷2)2
=3.14×62500
=196250(平方米)
答:我国FAST球面口的面积是196250平方米。
(2)(3.14×500)∶(3.14×305)
=1570∶957.7
=(1570×10)∶(957.7×10)
=15700∶9577
=(15700÷157)∶(9577÷157)
=100∶61
(3)500米=50000厘米
50∶50000
=(50÷50)∶(50000÷50)
=1∶1000
【点睛】根据圆的面积公式,周长公式,比的意义以及比例尺的意义进行解答。
13.(1)见详解
(2)O(4,1);图见详解
(3)见详解
【分析】(1)根据轴对称图形的特征:对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出关键对称点,依次连接即可;
(2)根据数对表示位置的方法:第一个数字表示列,第二个数字表示行;由此写出点O用数对表示;再根据旋转的特征:图①绕O点逆时针旋转90°,点O的位置不动,其余各部分均绕此点按相同的方向,旋转相同的度数,然后向上移动3格画出图形③;
(3)按1∶2的比例画出三角形缩小后的图形,就是把三角形的底和高分别缩小到原来的,原来的三角形的底和高分别是2格和4格,缩小后的底是2×=1格;高是4×=2格;据此画图即可。
【详解】(1)见下图;
(2)点C用数对表示为(7,5),则点O用数对表示为(4,1);见下图;
(3)底:2×=1(格);高:4×=2(格),见下图
【点睛】本题考查作轴对称图形,作平移后的图形,作旋转后的图形以及图形的放大或缩小。
14.(1)北;西;45
(2)1∶30000
(3)画见详解
【分析】(1)根据地图上方向的规定:上北下南,左西右东,以雷达站为观察点,说出A岛的位置;
(2)根据比例尺的意义:比例尺=图上距离∶实际距离;量出雷达站到A岛的图上距离,即可求解答;
(3)根据图上距离和实际距离的换算,求出B岛到雷达站的图上距离,以雷达站为观察点,画出B岛的位置。
【详解】(1)A岛在雷达站的北偏西45°方向,距离雷达站600米处;
(2)量出雷达站到A岛的图上距离是2厘米。
600米=60000厘米
比例尺:2∶60000
=(2÷2)∶(60000÷2)
=1∶30000
(3)900米=90000厘米
90000×
=3(厘米)
图如下:
【点睛】本题考查比例尺的意义,图上距离和实际距离的换算以及根据方向、角度和距离确定位置的方法进行解答,
15.108公顷
【分析】图上距离和比例尺已知,依据“实际距离=图上距离÷比例尺”即可求出长和宽的实际长度,再根据长方形的面积公式求出面积,然后转化单位即可。
【详解】长:2.4÷=120000(厘米)=1200米
宽:1.8÷=90000(厘米)=900米
1200×900=1080000(平方米)
1080000平方米=108公顷
答:该公园的占地面积约108公顷。
【点睛】掌握图上距离和实际距离的换算方法是解题的关键。
16.84千米
【分析】根据“实际距离=图上距离∶比例尺”代入数值求出实际距离,然后设乙车每小时行驶是x千米,根据(甲车的速度+乙车的速度)×时间=实际距离,解答即可。
【详解】5÷=75000000(厘米)
75000000厘米=750千米
解:设乙车每小时行x千米。
(66+x)×5=750
66+x=150
x=84
答:乙车每小时行84千米。
【点睛】此题主要考查比例尺、图上距离、实际距离三者的关系式:比例尺=图上距离∶实际距离,灵活变形列式解决问题。
17.24人
【分析】设乙车间原来有x人,根据甲、乙两个车间原来人数比为7∶3,找出关系式,列出方程:,解答即可。
【详解】解:设乙车间原来有x人。
答:乙车间原来有24人。
【点睛】解答此题的关键是先求出甲车间的人数,根据甲、乙两个车间原来人数比为7∶3,进而列比例求解。
18.(1)(2,8);(10,3)
(2)(3)(4)(5)见详解
【分析】(1)根据数对表示位置的方法:第一个数表示列,第二个数表示行,写出点B、点C的数对表示;
(2)根据轴对称图形的特征:对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右面画出图形①的关键对称点,依次连接即可得到图形;
(3)根据平移的特征:把图形①的各顶点分别向左平移6格,再向下平移2格,首尾连接得到平移后的图形;
(4)根据旋转的特征,将图形②绕点A逆时针旋转90°后,点A的位置不动,其余各部分均绕此点按相同的方向旋转相同的度数,即可画出旋转后的图形;
(5)按1∶2的比化成图形③缩小后的图形,就是把长方形的长和宽分别缩小原来的,原来的长和宽分别是4和2;缩小后的长和宽分别是2和1,作图即可得到缩小后的图形。
【详解】(1)B(2,8);C(10,3)
(2)见下图
(3)见下图
(4)见下图
(5)4×=2;2×=1,见下图:
【点睛】本题考查数对表示位置的方法、补全轴对称图形、作平移后的图形、作旋转后的图形以及图上的缩小。
19.(1)奶奶从小明家出发,向西走100米到达邮局,再从邮局向西偏北走100米到商场,最后从商场向西走100米到达医院。
(2)图见详解
【分析】(1)根据图形从方向、角度和距离方面可描述奶奶从小明家去医院的线路;
(2)根据图上距离=实际距离×比例尺,求出饭店到医院的图上距离,然后根据方向画出位置,据此解答。
【详解】(1)奶奶从小明家出发,向西走100米到达邮局,再从邮局向西偏北走100米到商场,最后从商场向西走100米到达医院。
(2)200米=20000厘米
20000×=2(厘米)
画图如下:
【点睛】根据方向、角度和距离描述线路图,以及图上距离和实际距离的换算进行解答。
20.8000元;6000元
【分析】可以设兄弟两人月收入分别为4x元,3x元,由于月结余均3600元,由此即可知道兄弟两人分别花的钱数,即4x-3600;3x-3600,由于月支出的比为11∶6,由此即可根据比例的意义列出方程,即(4x-3600)∶(3x-3600)=11∶6,再根据比例的基本性质和等式的性质解方程即可,之后再分别乘兄弟两人月收入的份数即可。
【详解】解:设兄弟两人月收入分别为4x元,3x元
(4x-3600)∶(3x-3600)=11∶6
6×(4x-3600)=11×(3x-3600)
24x-21600=33x-39600
33x-24x=39600-21600
9x=18000
x=18000÷9
x=2000
2000×4=8000(元)
2000×3=6000(元)
答:兄弟两人每个月的收入分别是8000元、6000元。
【点睛】本题主要考查比例的应用,要找准等量关系是解答关键。
21.(1)A(5,3),C (2,6)
(2)(3)作图见详解
放大后的图形与原三角形面积比是4∶1。
(4)A点在C点的南偏东45度方向。
【分析】(1)根据数对的知识可知,A点的位置是(5,3),C点的位置是:(2,6)。
(2)根据旋转图形的定义可知,将线段BC和BA顺时针旋转90度后,连接C、A旋转90度后各自对应的端点,即可得到这个三角形绕B点顺时针旋转90°后的图形。
(3)根据比的定义可知,把三角ABC按2:1扩大,就是把它的两条直角边扩大2倍,于是就画出了如详解图中所示的三角形EDF,根据三角形的面积公式可知扩大后的图形与原三角形面积比是4∶1。
(4)根据方向和位置的知识点可知,由图意可以知道,A点在C点的南偏东45度方向,
【详解】(1)A(5,3),C(2,6)
(2)
(3)
放大后的图形与原三角形面积比:
(6×6÷2)∶(3×3÷2)
=18∶4.5
=4∶1
(4)由图知:三角形BAC是等腰直角三角形,∠C=∠A=45
以C点为观察点,A点在C点的南偏东45度方向。
【点睛】本题是道综合题,考查了用数对表示位置、图形的旋转、图形的放大与缩小、三角形面积等知识。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
比例应用题易错汇编-数学六年级下册北师大版
1.一幅中国交通地图比例尺为在这幅地图上量得甲、乙两座城市之间相距6厘米,一辆出租车从甲城开出,3.75小时后到达乙城。出租车平均每小时行多少千米?
2.看图填一填,画一画。
(1)新华书店到学校的实际距离是( )米。
(2)小月家在学校北偏东45°方向,实际距离为900米的地方,请在图中标出小月家的位置。
3.某核酸检测点进行了为期三天的核酸检测,第一天有450人进行了核酸检测,第二天进行核酸检测的人数比第一天多,第三天与第二天进行核酸检酬的人数比是,该检测点第三天有多少人进行了核酸检测?(用比例解答)
4.一个机器实际零件长5毫米,画在比例尺是的图纸上,应画多少厘米?
5.如图,已知小红家到体育场的实际距离是7.5km。
(1)这幅图的比例尺是多少?
(2)从小红家到游乐园,实际要走多少千米?
(3)已知博物馆在游乐园的西偏北方向,实际距离为10km的地方,请在图中标出博物馆的位置。
6.将一个长25米,宽15米的长方形按1∶500的比例尺画在图纸上,该长方形在图纸上的面积是多少平方厘米?
7.某社区在封控时招募了216名志愿者,其中女性占,后来又来了若干名女性志愿者,使女性志愿者与男性志愿者的人数之比是3∶7,后来又来了多少名女性志愿者?(用比例解)
8.已知点A用数对表示为(3,6),按要求填一填,画一画。
(1)点B用数对表示为( ),点C用数对表示为( )。
(2)将图形①先向下平移3格,再向右平移2格。
(3)将图形①绕点C顺时针旋转90°。
(4)将图形①放大,使得放大后的图形与原图形对应线段长的比是2∶1。
9.下图是欢欢设计的冰激凌盒。如果按图中的比例尺制作成成品,成品的容积是多少?(材料厚度忽略不计)
10.在比例尺是1∶1000的平面图上,量得长方形操场的长是12厘米,宽是6厘米。如果把操场的面积按5∶4划分出篮球区和排球区,那么篮球区的面积是多少?
11.希望小学装修多媒体教室,计划用边长4分米的方砖铺地。需要800块。实际用边长8分米的正方形大理石铺地,则需要多少块正方形大理石?
12.“中国天眼”是目前全球最大的球面射电望远镜(简称FAST),它的球面口为圆,口径500米,与美国阿雷西博(Arecibo)305米口径望远镜相比,其综合性能提高约10倍。FAST将在未来20年保持世界一流设备的地位,成为世界天文学研究的“利器”。
(1)我国FAST球面口的面积是多少平方米?
(2)我国FAST与美国Arecibo球面口周长的最简比是( )。
(3)我国科学家在设计FAST时,设计图纸上的球面口直径是50cm,这幅设计图的比例尺是( )。
13.填一填、画一画(下面每个小正方形的边长表示1厘米)。
(1)画出图①关于直线CD对称的图形②;
(2)点C用数对表示为(7,5),则点O用数对表示为( );画出图①绕O点逆时针旋转90°,然后向上移动3格后的图形③;
(3)在方格纸的右下方画出图形①按1∶2缩小后的图形④。
14.以雷达站为观测点。
(1)A岛在雷达站的( )偏( )( )°方向,距离雷达站600米处。
(2)这幅图的比例尺是( )。
(3)B岛在雷达站的北偏东60°方向,距离雷达站的实际距离是900米,按比例尺画出从雷达站到B岛的线段,标出B岛的位置。
15.在一幅比例尺为1∶50000的地图上,欢欢发现某公园的占地接近于一个长方形。她用直尺量得这个长方形的长为2.4cm,宽为1.8cm。请你根据以上信息测算出该公园的占地面积约多少公顷?
16.在一幅比例尺是1∶15000000的地图上,A地到B地的图上距离是5厘米,甲、乙两车同时从A,B两地相向而行,甲车每小时行66千米,5小时后两车相遇,乙车每小时行多少千米?
17.甲,乙两个车间原来人数比为7∶3,甲车间人数调出后,还剩42人,乙车间原来有多少人?(用比例解)
18.按要求填一填,画一画。
(1)点A的位置用数对表示,点B的位置用数对( )表示,点C的位置用数对( )表示。
(2)以虚线为对称轴,画出图形①的轴对称图形。
(3)将图形①先向左平移6格,再向下平移2格。
(4)将图形②绕点A逆时针旋转90度。
(5)将图形③缩小,使得缩小后的图形与原图形对应线段长的比是。
19.下面是小明家位置图,按要求回答:
(1)奶奶生病了,请你用文字描述奶奶从小明家去医院看病所走的线路。
(2)看完病,奶奶有点饿了,想在医院的正西方向距医院200米的饭店就餐,请在图中用★标出饭店的位置并写出计算过程。
20.兄弟两人月收入的比为4∶3,月支出比为11∶6,月结余均为3600元,问每人每月收入多少元?
21.请按要求完成:
(1)将图中A点、C点的位置分别用数对表示出来:( )、( )。
(2)画出这个三角形绕B点顺时针旋转90°后的图形。
(3)按2∶1画出这个三角形放大后的图形,放大后的图形与原三角形面积比是( )。
(4)从图中可知,A点在C点的( )偏( )( )°方向。
参考答案:
1.80千米
【分析】根据实际距离=图上距离÷比例尺,代入数据,求出甲、乙两座城市之间的实际距离,再根据速度=路程÷时间,代入数据,即可解答。
【详解】6÷
=6×5000000
=30000000(厘米)
30000000厘米=300(千米)
300÷3.75=80(千米)
答:出租车平均每小时行80千米。
【点睛】本题考查实际距离和图上距离的换算,以及根据速度、时间和路程三者的关系解答问题,注意单位名数之间的换算。
2.(1)600
(2)见详解
【分析】(1)通过测量,新华书店到学校的图上距离是2厘米;根据实际距离=图上距离÷比例尺,代入数据,求出新华书店到学校的实际距离;
(2)根据地图上方向的规定:上北下南,左西右东;以学校的位置为观测点,即可确定小月家方向,再根据学校与小月家的实际距离以及图中所标注的比例尺,求出学校与小月家的图上距离,从而在图中标出小月家的位置。
【详解】(1)量得新华书店到学校的图上距离是2厘米。
2÷
=2×30000
=60000(厘米)
60000厘米=600米
新华书店到学校的实际距离是600米。
(2)900米=90000厘米
90000×=3(厘米)
【点睛】本题利用方向和距离在平面图中确定物体位置的方法以及比例尺的灵活应用,画平面图的关键一是方向的确定,二是根据实际距离以及比例尺求出图上距离。
3.660人
【分析】把第一天进行核酸检测的人数看作单位“1”,第二天进行核酸检测的人数是第一天的(1+),用第一天核酸检测人数×(1+),求出第二天核酸检测人数;
设该核酸检查点第三天核酸检测人数是x人,根据第三天与第二天进行核酸检测的人数比是11∶9,列比例:x∶第二天核酸检测人数=11∶9,解比例,即可解答。
【详解】450×(1+)
=450×
=540(人)
解:设该核酸检查点第三天有x人进行核酸检测。
x∶540=11∶9
9x=540×11
9x=5940
x=5940÷9
x=660
答:该核酸检测点第三天有660人进行了核酸检测。
【点睛】本题先根据分数乘法的意义,求出第二天核酸检测的人数,再根据比例的基本性质,求出第三天核酸检测的人数。
4.4厘米
【分析】图上距离=实际距离×比例尺,代入数据,即可解答。
【详解】5毫米=0.5厘米
0.5×8=4(厘米)
答:应画4厘米。
【点睛】本题考查实际距离和图上距离之间的换算,注意单位名数的统一。
5.(1)1∶500000
(2)35千米
(3)见详解
【分析】(1)根据小红家到体育场的实际距离,再量出小红家到体育场的图上距离,根据比例尺的意义:比例尺=图上距离∶实际距离,求出这幅图的比例尺;
(2)量出小红家到游乐园的图上距离;再根据实际距离=图上距离÷比例尺,求出这幅图小红家到游乐园的实际距离;
(3)根据图上距离=实际距离×比例尺,代入数据,求出游乐园到博物馆的图上距离;再以游乐园为观测点,根据方向,角度和距离,画出博物馆的位置。
【详解】(1)量出小红家到体育场的图上距离是1.5厘米。
7.5千米=750000厘米
1.5∶750000
=(1.5÷1.5)∶(750000÷1.5)
=1∶500000
答:这幅图的比例尺是1∶500000。
(2)量出小红家到游乐园的图上距离是7厘米。
7÷
=7×500000
=3500000(厘米)
3500000厘米=35千米
答:从小红家到游乐园,实际要走35千米。
(3)10千米=1000000厘米
1000000×=2(厘米)
【点睛】本题考查比例尺的意义,图上距离和实际距离之间的换算,以及根据方向、角度和距离确定物体位置。
6.15平方厘米
【分析】实际距离和比例尺已知,根据“图上距离=实际距离×比例尺”即可分别求出长方形的长和宽的图上距离,利用长方形的面积S=ab即可求出它的图上面积。
【详解】25米=2500厘米
15米=1500厘米
2500×=5(厘米)
1500×=3(厘米)
5×3=15(平方厘米)
答:该长方形在图纸上的面积是15平方厘米。
【点睛】此题主要考查图上距离、实际距离和比例尺的关系以及长方形的面积的计算方法,解答时要注意单位的换算。
7.24名
【分析】根据原来女性占总人数的分率,求出女性和男性的人数,再设后来来了x名女性,根据女性和男性人数比,列比例求解。
【详解】原来女性人数:216×=48(名)
男性人数:216-48=168(名)
解:设后来来了x名女性。
(48+x)∶168=3∶7
7×(48+x)=3×168
336+7x=504
336+7x-336=504-336
7x=168
7x÷7=168÷7
x=24
答:后来又来了24名女性志愿者。
【点睛】本题主要考查比例的应用,关键注意男性志愿者的人数没有改变。
8.(1)B(1,4);C(5,4)
(2)(3)(4)见详解
【分析】(1)根据数对的表示方法:第一个数字表示列,第二个数字表示行,由此即可用数对表示出点B和点C。
(2)根据平移的特征,把图形①各顶点分别向下平移3格,再向右平移2格,依次连结即可得到向下平移3格,再向右平移2格后的图形。
(3)根据旋转的特征,图形①绕点C顺时针旋转90°,点C的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(4)按2∶1把图形①放大,则放大后的图形各边的长度是图形①的2倍。
【详解】(1)B(1,4);C(5,4)
(2)(3)(4)如下图所示:
【点睛】本题考查的知识点比较多,要熟练掌握图形的旋转,平移的画法以及图形的放大和用数对表示位置的方法并灵活运用。
9.84.78立方厘米
【分析】根据实际距离=图上距离÷比例尺,代入数据,取出冰激凌的底面直径和高的实际长度,再根据圆锥体的体积公式:体积=底面积×高×,代入数据,即可解答。
【详解】冰激凌的底面直径:
1÷
=1×6
=6(厘米)
冰激凌的高:
1.5÷
=1.5×6
=9(厘米)
3.14×(6÷2)2×9×
=3.14×9×9×
=28.26×9×
=254.34×
=84.78(立方厘米)
答:成品的容积是84.78立方厘米。
【点睛】利用实际距离和图上距离之间的换算,以及圆锥的体积公式进行解答。
10.4000平方米
【分析】根据“图上距离÷比例尺=实际距离”,代入数值分别计算出操场实际的长和宽,然后根据“长方形的面积=长×宽”,代入数值计算可求得操场的实际面积,由于这个操场按5∶4划出篮球区和排球区,所以篮球区的面积是操场实际面积的,用操场实际面积乘就是篮球区的面积;据此解答。
【详解】12÷=12000(厘米)
12000厘米=120米
6÷=6000(厘米)
6000厘米=60米
60×120=7200(平方米)
7200×
=7200×
=4000(平方米)
答:篮球区的面积是4000平方米。
【点睛】解答此题用到的知识点:(1)图上距离、实际距离和比例尺三者之间的关系;(2)长方形的面积计算方法。
11.200块
【分析】多媒体教室的面积不变,所以所需方砖的块数×每块方砖的面积=多媒体教室的面积(一定),乘积一定,所以所需方砖的块数和每块方砖的面积成反比例关系,据此设出未知数,列比例解答即可。
【详解】解:设用边长8分米的正方形大理石铺地,则需要x块正方形大理石。
4×4×800=8×8x
64x=12800
64x÷64=12800÷64
x=200
答:用边长8分米的正方形大理石铺地,则需要200块正方形大理石。
【点睛】明确题中所需方砖的块数和每块方砖的面积成反比例关系是解题的关键。
12.(1)196250平方米
(2)100∶61
(3)1∶1000
【分析】(1)根据圆的面积公式:面积=π×半径2;代入数据,求出面积;
(2)根据圆的周长公式:周长=π×直径;代入数据,分别求出我国FAST和美国Arecibo球面口周长,再根据比的意义,进行解答;
(3)根据比例尺的意义:比例尺=图上距离∶实际距离,代入数据,求出这幅设计的比例尺。
【详解】(1)3.14×(500÷2)2
=3.14×62500
=196250(平方米)
答:我国FAST球面口的面积是196250平方米。
(2)(3.14×500)∶(3.14×305)
=1570∶957.7
=(1570×10)∶(957.7×10)
=15700∶9577
=(15700÷157)∶(9577÷157)
=100∶61
(3)500米=50000厘米
50∶50000
=(50÷50)∶(50000÷50)
=1∶1000
【点睛】根据圆的面积公式,周长公式,比的意义以及比例尺的意义进行解答。
13.(1)见详解
(2)O(4,1);图见详解
(3)见详解
【分析】(1)根据轴对称图形的特征:对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出关键对称点,依次连接即可;
(2)根据数对表示位置的方法:第一个数字表示列,第二个数字表示行;由此写出点O用数对表示;再根据旋转的特征:图①绕O点逆时针旋转90°,点O的位置不动,其余各部分均绕此点按相同的方向,旋转相同的度数,然后向上移动3格画出图形③;
(3)按1∶2的比例画出三角形缩小后的图形,就是把三角形的底和高分别缩小到原来的,原来的三角形的底和高分别是2格和4格,缩小后的底是2×=1格;高是4×=2格;据此画图即可。
【详解】(1)见下图;
(2)点C用数对表示为(7,5),则点O用数对表示为(4,1);见下图;
(3)底:2×=1(格);高:4×=2(格),见下图
【点睛】本题考查作轴对称图形,作平移后的图形,作旋转后的图形以及图形的放大或缩小。
14.(1)北;西;45
(2)1∶30000
(3)画见详解
【分析】(1)根据地图上方向的规定:上北下南,左西右东,以雷达站为观察点,说出A岛的位置;
(2)根据比例尺的意义:比例尺=图上距离∶实际距离;量出雷达站到A岛的图上距离,即可求解答;
(3)根据图上距离和实际距离的换算,求出B岛到雷达站的图上距离,以雷达站为观察点,画出B岛的位置。
【详解】(1)A岛在雷达站的北偏西45°方向,距离雷达站600米处;
(2)量出雷达站到A岛的图上距离是2厘米。
600米=60000厘米
比例尺:2∶60000
=(2÷2)∶(60000÷2)
=1∶30000
(3)900米=90000厘米
90000×
=3(厘米)
图如下:
【点睛】本题考查比例尺的意义,图上距离和实际距离的换算以及根据方向、角度和距离确定位置的方法进行解答,
15.108公顷
【分析】图上距离和比例尺已知,依据“实际距离=图上距离÷比例尺”即可求出长和宽的实际长度,再根据长方形的面积公式求出面积,然后转化单位即可。
【详解】长:2.4÷=120000(厘米)=1200米
宽:1.8÷=90000(厘米)=900米
1200×900=1080000(平方米)
1080000平方米=108公顷
答:该公园的占地面积约108公顷。
【点睛】掌握图上距离和实际距离的换算方法是解题的关键。
16.84千米
【分析】根据“实际距离=图上距离∶比例尺”代入数值求出实际距离,然后设乙车每小时行驶是x千米,根据(甲车的速度+乙车的速度)×时间=实际距离,解答即可。
【详解】5÷=75000000(厘米)
75000000厘米=750千米
解:设乙车每小时行x千米。
(66+x)×5=750
66+x=150
x=84
答:乙车每小时行84千米。
【点睛】此题主要考查比例尺、图上距离、实际距离三者的关系式:比例尺=图上距离∶实际距离,灵活变形列式解决问题。
17.24人
【分析】设乙车间原来有x人,根据甲、乙两个车间原来人数比为7∶3,找出关系式,列出方程:,解答即可。
【详解】解:设乙车间原来有x人。
答:乙车间原来有24人。
【点睛】解答此题的关键是先求出甲车间的人数,根据甲、乙两个车间原来人数比为7∶3,进而列比例求解。
18.(1)(2,8);(10,3)
(2)(3)(4)(5)见详解
【分析】(1)根据数对表示位置的方法:第一个数表示列,第二个数表示行,写出点B、点C的数对表示;
(2)根据轴对称图形的特征:对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右面画出图形①的关键对称点,依次连接即可得到图形;
(3)根据平移的特征:把图形①的各顶点分别向左平移6格,再向下平移2格,首尾连接得到平移后的图形;
(4)根据旋转的特征,将图形②绕点A逆时针旋转90°后,点A的位置不动,其余各部分均绕此点按相同的方向旋转相同的度数,即可画出旋转后的图形;
(5)按1∶2的比化成图形③缩小后的图形,就是把长方形的长和宽分别缩小原来的,原来的长和宽分别是4和2;缩小后的长和宽分别是2和1,作图即可得到缩小后的图形。
【详解】(1)B(2,8);C(10,3)
(2)见下图
(3)见下图
(4)见下图
(5)4×=2;2×=1,见下图:
【点睛】本题考查数对表示位置的方法、补全轴对称图形、作平移后的图形、作旋转后的图形以及图上的缩小。
19.(1)奶奶从小明家出发,向西走100米到达邮局,再从邮局向西偏北走100米到商场,最后从商场向西走100米到达医院。
(2)图见详解
【分析】(1)根据图形从方向、角度和距离方面可描述奶奶从小明家去医院的线路;
(2)根据图上距离=实际距离×比例尺,求出饭店到医院的图上距离,然后根据方向画出位置,据此解答。
【详解】(1)奶奶从小明家出发,向西走100米到达邮局,再从邮局向西偏北走100米到商场,最后从商场向西走100米到达医院。
(2)200米=20000厘米
20000×=2(厘米)
画图如下:
【点睛】根据方向、角度和距离描述线路图,以及图上距离和实际距离的换算进行解答。
20.8000元;6000元
【分析】可以设兄弟两人月收入分别为4x元,3x元,由于月结余均3600元,由此即可知道兄弟两人分别花的钱数,即4x-3600;3x-3600,由于月支出的比为11∶6,由此即可根据比例的意义列出方程,即(4x-3600)∶(3x-3600)=11∶6,再根据比例的基本性质和等式的性质解方程即可,之后再分别乘兄弟两人月收入的份数即可。
【详解】解:设兄弟两人月收入分别为4x元,3x元
(4x-3600)∶(3x-3600)=11∶6
6×(4x-3600)=11×(3x-3600)
24x-21600=33x-39600
33x-24x=39600-21600
9x=18000
x=18000÷9
x=2000
2000×4=8000(元)
2000×3=6000(元)
答:兄弟两人每个月的收入分别是8000元、6000元。
【点睛】本题主要考查比例的应用,要找准等量关系是解答关键。
21.(1)A(5,3),C (2,6)
(2)(3)作图见详解
放大后的图形与原三角形面积比是4∶1。
(4)A点在C点的南偏东45度方向。
【分析】(1)根据数对的知识可知,A点的位置是(5,3),C点的位置是:(2,6)。
(2)根据旋转图形的定义可知,将线段BC和BA顺时针旋转90度后,连接C、A旋转90度后各自对应的端点,即可得到这个三角形绕B点顺时针旋转90°后的图形。
(3)根据比的定义可知,把三角ABC按2:1扩大,就是把它的两条直角边扩大2倍,于是就画出了如详解图中所示的三角形EDF,根据三角形的面积公式可知扩大后的图形与原三角形面积比是4∶1。
(4)根据方向和位置的知识点可知,由图意可以知道,A点在C点的南偏东45度方向,
【详解】(1)A(5,3),C(2,6)
(2)
(3)
放大后的图形与原三角形面积比:
(6×6÷2)∶(3×3÷2)
=18∶4.5
=4∶1
(4)由图知:三角形BAC是等腰直角三角形,∠C=∠A=45
以C点为观察点,A点在C点的南偏东45度方向。
【点睛】本题是道综合题,考查了用数对表示位置、图形的旋转、图形的放大与缩小、三角形面积等知识。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
