新人教A版必修第二册2024春高中数学第8章 立体几何初步 章末综合测评(含解析)
文档属性
| 名称 | 新人教A版必修第二册2024春高中数学第8章 立体几何初步 章末综合测评(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 495.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-13 13:29:49 | ||
图片预览


文档简介
章末综合测评(三) 立体几何初步
(时间:120分钟 满分:150分)
一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列条件中,能确定一个平面的是( )
A.空间中任意三点
B.空间中两条直线
C.空间中两条相交直线
D.一条直线和一个点
2.一个棱柱的侧面展开图是三个全等的矩形,矩形的长和宽分别为6 cm,4 cm,则该棱柱的侧面积为( )
A.24 cm2 B.36 cm2
C.72 cm2 D.84 cm2
3.(2022·厦门一中月考)如图,平行四边形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=5,O′C′=2,∠A′O′C′=30°,则原图形的面积是( )
A.4 B.10 C.4 D.5
4.(2022·新高考Ⅰ卷)南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔148.5 m时,相应水面的面积为140.0 km2;水位为海拔157.5 m时,相应水面的面积为180.0 km2,将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔148.5 m上升到157.5 m时,增加的水量约为(≈2.65)( )
A.1.0×109 m3 B.1.2×109 m3
C.1.4×109 m3 D.1.6×109 m3
5.(2021·全国乙卷)在正方体ABCD-A1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为( )
A. B. C. D.
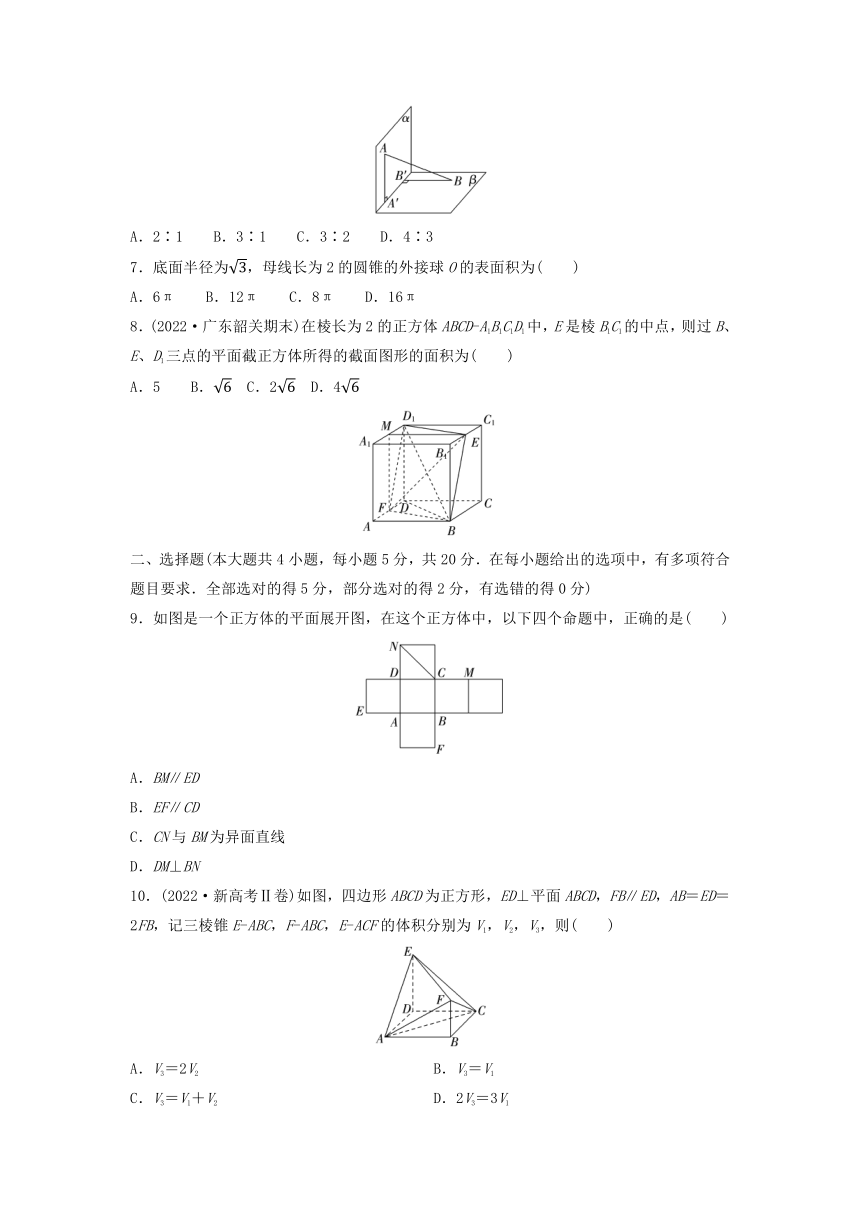
6.如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α,β所成的角分别为和.过A,B分别作两平面交线的垂线,垂足为A′,B′,则AB∶A′B′等于( )
A.2∶1 B.3∶1 C.3∶2 D.4∶3
7.底面半径为,母线长为2的圆锥的外接球O的表面积为( )
A.6π B.12π C.8π D.16π
8.(2022·广东韶关期末)在棱长为2的正方体ABCD-A1B1C1D1中,E是棱B1C1的中点,则过B、E、D1三点的平面截正方体所得的截面图形的面积为( )
A.5 B. C.2 D.4
二、选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.如图是一个正方体的平面展开图,在这个正方体中,以下四个命题中,正确的是( )
A.BM∥ED
B.EF∥CD
C.CN与BM为异面直线
D.DM⊥BN
10.(2022·新高考Ⅱ卷)如图,四边形ABCD为正方形,ED⊥平面ABCD,FB∥ED,AB=ED=2FB,记三棱锥E-ABC,F-ABC,E-ACF的体积分别为V1,V2,V3,则( )
A.V3=2V2 B.V3=V1
C.V3=V1+V2 D.2V3=3V1
11.如图是四棱锥的平面展开图,其中四边形ABCD为正方形,E,F,G,H分别为PA,PD,PC,PB的中点,在此几何体中,给出下面四个结论,其中正确的有( )
A.平面EFGH∥平面ABCD
B.BC∥平面PAD
C.AB∥平面PCD
D.平面PAD∥平面PAB
12.如图,已知长方体ABCD-A1B1C1D1中,四边形ABCD为正方形,AB=2,AA1=,E,F分别为AB,BC的中点.则( )
A.A1E⊥DF
B.点A1、E、F、C1四点共面
C.直线C1D与平面BB1C1C所成角的正切值为
D.三棱锥E-C1DF的体积为
三、填空题(本大题共4小题,每小题5分,共20分)
13.如果用半径R=2的半圆形铁皮卷成一个圆锥筒,那么这个圆锥筒的高是 .
14.如图,在三棱柱A1B1C1-ABC中,D,E,F分别是AB,AC,AA1的中点,设三棱锥F-ADE的体积为V1,三棱柱A1B1C1-ABC的体积为V2,则V1∶V2= .
15.如图,若边长为4和3与边长为4和2的两个矩形所在的平面互相垂直,则cos α∶cos β= .
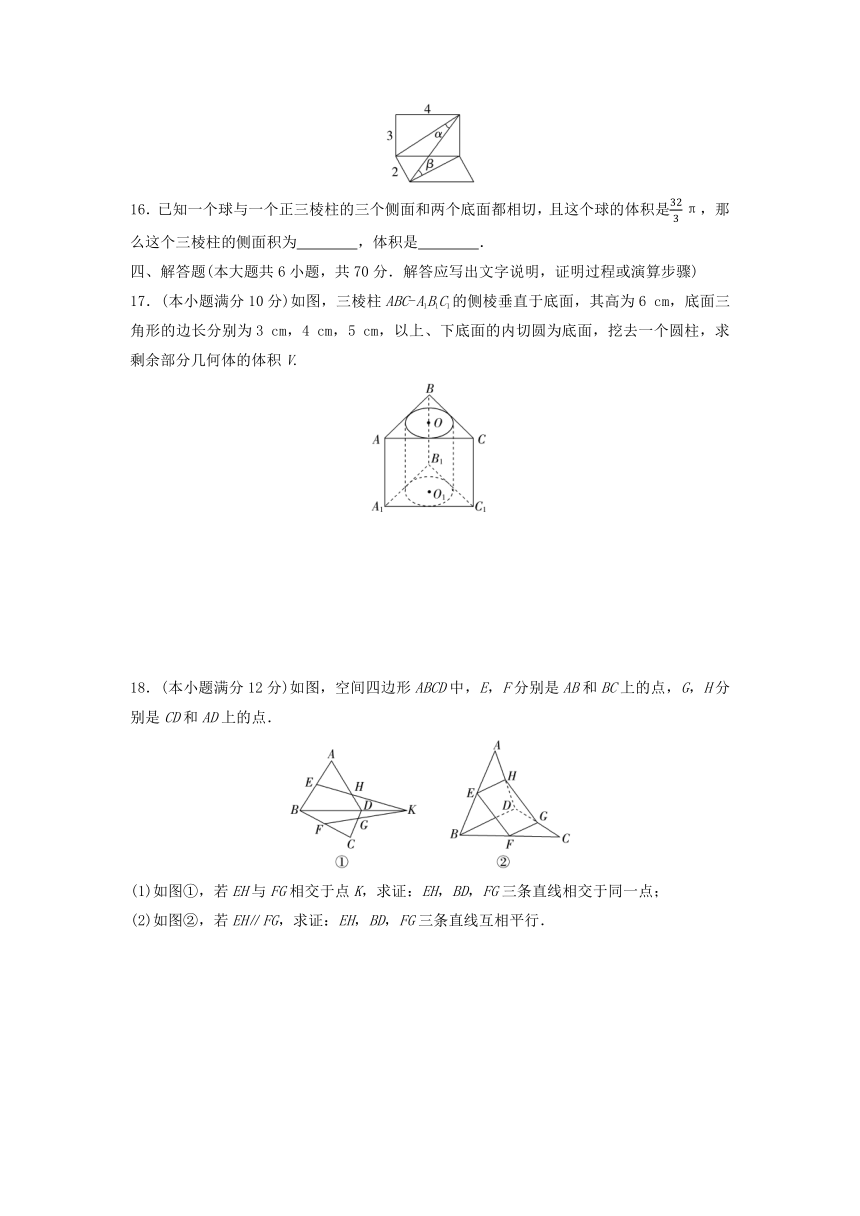
16.已知一个球与一个正三棱柱的三个侧面和两个底面都相切,且这个球的体积是那么这个三棱柱的侧面积为 ,体积是 .
四、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,其高为6 cm,底面三角形的边长分别为3 cm,4 cm,5 cm,以上、下底面的内切圆为底面,挖去一个圆柱,求剩余部分几何体的体积V.
18.(本小题满分12分)如图,空间四边形ABCD中,E,F分别是AB和BC上的点,G,H分别是CD和AD上的点.
(1)如图①,若EH与FG相交于点K,求证:EH,BD,FG三条直线相交于同一点;
(2)如图②,若EH∥FG,求证:EH,BD,FG三条直线互相平行.
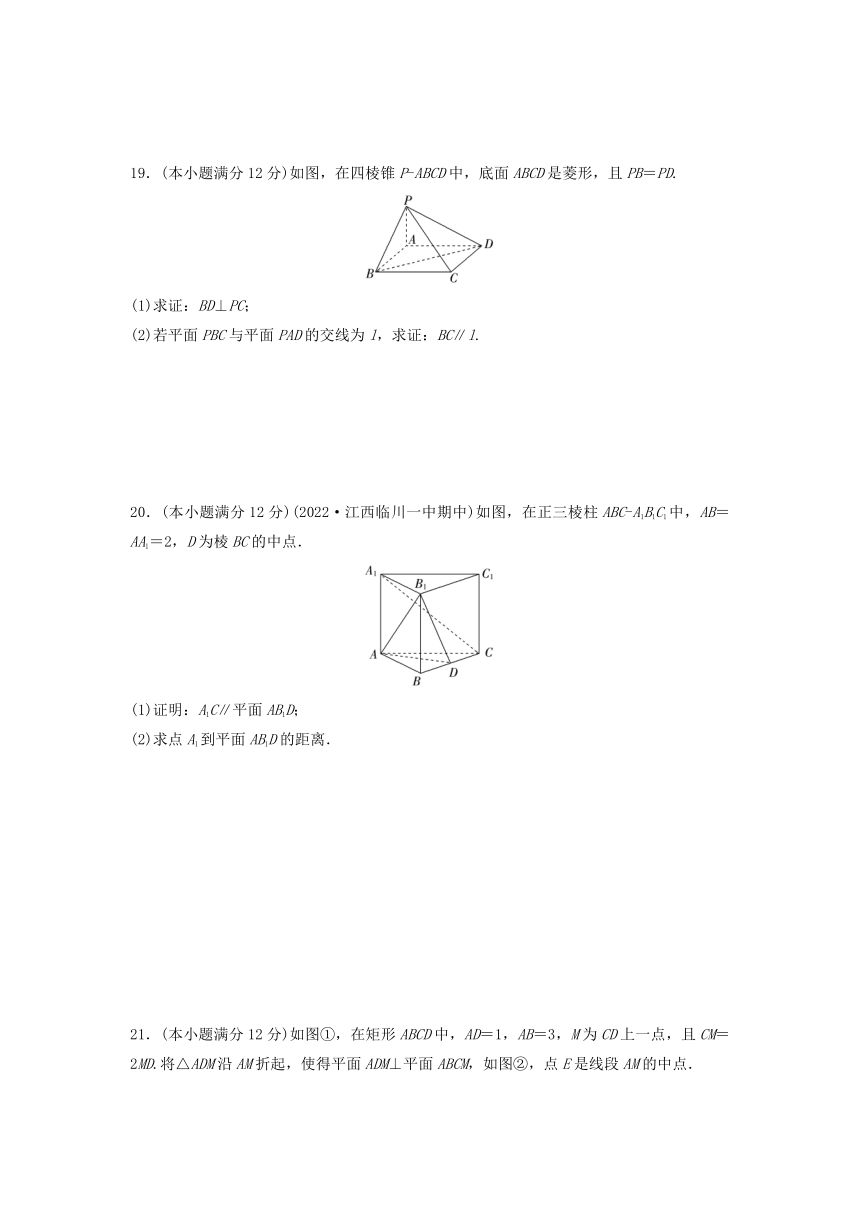
19.(本小题满分12分)如图,在四棱锥P-ABCD中,底面ABCD是菱形,且PB=PD.
(1)求证:BD⊥PC;
(2)若平面PBC与平面PAD的交线为l,求证:BC∥l.
20.(本小题满分12分)(2022·江西临川一中期中)如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,D为棱BC的中点.
(1)证明:A1C∥平面AB1D;
(2)求点A1到平面AB1D的距离.
21.(本小题满分12分)如图①,在矩形ABCD中,AD=1,AB=3,M为CD上一点,且CM=2MD.将△ADM沿AM折起,使得平面ADM⊥平面ABCM,如图②,点E是线段AM的中点.
(1)求证:平面BDE⊥平面ABCM;
(2)过B点是否存在一条直线l,同时满足以下两个条件:①l 平面ABCM;②l⊥AD.请说明理由.
22.(本小题满分12分)(2022·贵州月考)在我国古代数学名著《九章算术》中将由四个直角三角形组成的四面体称为“鳖臑(nào)”.如图,在三棱锥P-ABC中,PA⊥平面ABC,PA=BC=,AB=1,AC=2,E为棱PB上一点.
(1)若AE⊥平面PBC,求VP-ACE∶VE-ABC;
(2)求二面角A-PC-B的余弦值.
章末综合测评(三) 立体几何初步
1.C [对于A,空间任意三点,当三点共线时能确定一条直线而不是平面,故错误;对于B,空间两条直线,当两条直线重合时,过这条直线的平面有无数个,故错误;对于C,空间两条相交直线,根据课本中的判定得到是正确的;对于D,一条直线和一个点,当这个点在直线上时,过这条直线的平面有无数个,故错误.故选C.]
2.C [棱柱的侧面积S侧=3×6×4=72(cm2).]
3.B [平行四边形O′A′B′C′中,O′A′=5,O′C′=2,∠A′O′C′=30°,所以平行四边形O′A′B′C′的面积为S′=O′A′·O′C′·sin 30°=5×2×=5,所以原平面图形的面积是S=2S′=2=.故选B.]
4.C [依题意可知棱台的高为MN=157.5-148.5=9(m),所以增加的水量即为棱台的体积V.
棱台下底面积S=140.0 km2=140×106m2,上底面积S′=180.0 km2=180×106m2,
∴V=h=×9×=3××106≈(96+18×2.65)×107=1.437×109≈1.4×109(m3).
故选C.]
5.D [法一:如图,连接C1P,因为ABCD-A1B1C1D1是正方体,
且P为B1D1的中点,所以C1P⊥B1D1,又C1P⊥BB1,所以C1P⊥平面B1BP.又BP 平面B1BP,所以C1P⊥BP.连接BC1,则AD1∥BC1,所以∠PBC1为直线PB与AD1所成的角.设正方体ABCD-A1B1C1D1的棱长为2,则在直角三角形C1PB中,C1P=,所以∠PBC1=,故选D.
法二:如图所示,连接BC1,A1B,A1P,PC1,则易知AD1∥BC1,所以直线PB与AD1所成角等于直线PB与BC1所成角.根据P为正方形A1B1C1D1的对角线B1D1的中点,易知A1,P,C1三点共线,且P为A1C1的中点.易知A1B=BC1=A1C1,所以△A1BC1为等边三角形,所以∠A1BC1=,又P为A1C1的中点,所以可得∠PBC1=∠A1BC1=.]
6.A [连接AB′,A′B(图略),由已知条件可知∠BAB′=,∠ABA′=,
设AB=2a,则BB′=2a sin a,
A′B=2a cos a,
∴在Rt△BB′A′中,得A′B′=a,
∴AB∶A′B′=2∶1.]
7.D [由题意,圆锥轴截面的顶角为120°,设该圆锥的底面圆心为O′,球O的半径为R,则O′O=R-1.
由勾股定理可得R2=(R-1)2+2,∴R=2,
∴球O的表面积为4πR2=16π.]
8.C [设平面BED1交棱AD于F,由正方体性质及平面与平面平行的性质定理得ED1∥BF,D1F∥BE,
由勾股定理可得四边形D1FBE所有边长的长度为,
所以D1FBE是菱形,且F为AD的中点,
取A1D1的中点M,连接FM,ME,
则D1B=
=,
EF=,
故=.故选C.]
9.BCD [作出正方体的直观图,如图,由直观图可知BM与DE为互相垂直的异面直线,故A错误;EF∥AB∥CD,故B正确;
CN与BM为异面直线,故C正确;
由正方体性质得BN⊥平面DEM,故NB⊥DM,故D正确.故选BCD.]
10.CD [设AB=ED=2FB=2,则V1===.连接BD交AC于M,连接EM、FM(图略),则FM=,EF=3,所以FM 2+EM 2=EF 2,∴EM⊥FM,故S△EMF=S△EMF×AC=2,V3=V1+V2,2V3=3V1,故选CD.]
11.ABC [把平面展开图还原为四棱锥如图所示,则EH∥AB,因为AB 平面ABCD,EH 平面ABCD,所以EH∥平面ABCD.同理可证EF∥平面ABCD,因为EH∩EF=E,EH,EF 平面EFGH,所以平面EFGH∥平面ABCD;平面PAD,平面PBC,平面PAB,平面PDC均是四棱锥的四个侧面,则它们两两相交.因为AB∥CD,CD 平面PCD,AB 平面PCD,所以AB∥平面PCD.同理,BC∥平面PAD.]
12.BCD [对于A,假设A1E⊥DF,由题意知BC⊥平面AA1B1B,A1E 平面AA1B1B,∴A1E⊥BC,又BC∩DF=F,∴A1E⊥平面ABCD,由长方体性质知A1E与平面ABCD不垂直,故假设不成立,故A错误;
对于B,连接EF,AC,A1C1,由于E,F分别为AB,BC的中点,∴EF∥AC,又因为长方体ABCD-A1B1C1D1,知A1C1∥AC,∴EF∥A1C1,所以点A1、E、F、C1四点共面,故B正确;
对于C,由题意可知DC⊥平面BB1C1C,∴∠DC1C为直线C1D与平面BB1C1C所成角,在Rt△DCC1中,CC1=,CD=2,则tan∠DC1C=,故C正确;
对于D,连接DE,C1E,∵AB=AD=2,则S△DEF=S□ABCD-S△ADE-S△BEF-S△CDF=2×2-利用等体积法知:==·S△DEF·CC1=,故D正确.故选BCD.]
13.3 [设圆锥筒的底面半径为r,则2πr=πR=2π,则r=,
所以圆锥筒的高h==3.]
14.1∶24 [因为D,E分别是AB,AC的中点,
所以S△ADE∶S△ABC=1∶4.又F是AA1的中点,
所以A1到底面的距离H为F到底面距离h的2倍,即三棱柱A1B1C1-ABC的高是三棱锥F-ADE高的2倍,所以V1∶V2==1∶24.]
15.∶2 [如图,设两个矩形分别为矩形ABCD、矩形ABEF,因为平面ABCD⊥平面ABEF,
平面ABCD∩平面ABEF=AB,
AF 平面ABEF,AF⊥AB,故AF⊥平面ABCD,而AC 平面ABCD,
所以AF⊥AC,同理CB⊥BF.
由题意,两个矩形的对角线长分别为5,2,
所以cos α=,cos β=,
所以cos α∶cos β=∶2.]
16.48 48 [设球的半径为r,则πr3=π,
得r=2,柱体的高为2r=4.
又正三棱柱的底面三角形的内切圆半径与球的半径相等,
所以底面正三角形的边长为4,
所以正三棱柱的侧面积S侧=3×4×4,
体积V=2×4=48.]
17.解:×3×4×6=36(cm3).
设圆柱底面圆的半径为r,则r===1,
=πr2h=6π(cm3).
所以V=-=(36-6π)cm3.
18.证明:(1)因为K∈EH,EH 平面ABD,
所以K∈平面ABD,同理K∈平面CBD,而平面ABD∩平面CBD=BD,因此K∈BD,
所以EH,BD,FG三条直线相交于同一点.
(2)因为EH∥FG,FG 平面BCD,EH 平面BCD,
所以EH∥平面BCD,而EH 平面ABD,平面ABD∩平面BCD=BD,
所以EH∥BD,而EH∥FG,所以EH∥FG∥BD.
19.证明:(1)如图,连接AC,交BD于点O,连接PO.
因为四边形ABCD为菱形,所以BD⊥AC.
又因为PB=PD,O为BD的中点,
所以BD⊥PO.
因为PO∩AC=O,所以BD⊥平面PAC,
因为PC 平面PAC,所以BD⊥PC.
(2)因为四边形ABCD为菱形,所以BC∥AD.
因为BC 平面PAD,AD 平面PAD,
所以BC∥平面PAD.
又因为BC 平面PBC,
平面PBC与平面PAD的交线为l,所以BC∥l.
20.解:(1)证明:连接A1B交AB1于O,连接OD,
正三棱柱ABC-A1B1C1中,易得O为AB1中点,
又D为BC的中点,所以OD∥A1C.
因为A1C 平面AB1D,OD 平面AB1D,
所以A1C∥平面AB1D.
(2)因为A1C∥平面AB1D,
所以C与A1到平面AB1D的距离相等,
由题意得AB1=2,
因为AD2+=,所以AD⊥DB1,
所以,S△ADC=,
设C到平面ADB1的距离为h,则,
所以×2,所以h=,
即点A1到平面AB1D的距离为.
21.解:(1)证明:由已知得DA=DM,E是AM的中点,所以DE⊥AM.
因为平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,所以DE⊥平面ABCM.
又DE 平面BDE,所以平面BDE⊥平面ABCM.
(2)过B点存在一条直线l,同时满足以下两个条件:①l 平面ABCM;②l⊥AD.
理由:
在平面ABCM中,
过点B作直线l,使l⊥AM(图略).
因为平面ADM⊥平面ABCM,平面ABCM∩平面ADM=AM,所以l⊥平面ADM,所以l⊥AD.
22.解:(1)因PA⊥平面ABC,BC 平面ABC,AB 平面ABC,则PA⊥BC,PA⊥AB,又AB2+BC2=AC2,即AB⊥BC.又PA∩AB=A,PA,AB 平面PAB,因此BC⊥平面PAB.
所以VP-ACE∶VE-ABC=VC-PAE∶VC-ABE=PE∶EB,
在Rt△PAB中,PB=2,由AE⊥平面PBC得AE⊥PB,则PA·AB=PB·AE,即有AE=,
在Rt△PAE中,PE=,则有EB=,所以VP-ACE∶VE-ABC=3∶1.
(2)如图,作AE⊥PB于点E,过点E作EO垂直PC于点O,连接AO.
由(1)知,BC⊥平面PAB,AE 平面PAB,则BC⊥AE,而PB∩BC=B,PB,BC 平面PBC,
于是得AE⊥平面PBC.
又PC 平面PBC,则AE⊥PC.
又EO⊥PC,AE,EO 平面AOE,AE∩EO=E,
则有PC⊥平面AOE,所以PC⊥AO.
因此∠AOE是二面角A-PC-B的平面角.
在Rt△PAC中,PC=,
则AO=.
由(1)知,AE=,
在Rt△AOE中,sin ∠AOE=,
则cos ∠AOE=,
所以二面角A-PC-B的余弦值是.
(时间:120分钟 满分:150分)
一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列条件中,能确定一个平面的是( )
A.空间中任意三点
B.空间中两条直线
C.空间中两条相交直线
D.一条直线和一个点
2.一个棱柱的侧面展开图是三个全等的矩形,矩形的长和宽分别为6 cm,4 cm,则该棱柱的侧面积为( )
A.24 cm2 B.36 cm2
C.72 cm2 D.84 cm2
3.(2022·厦门一中月考)如图,平行四边形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=5,O′C′=2,∠A′O′C′=30°,则原图形的面积是( )
A.4 B.10 C.4 D.5
4.(2022·新高考Ⅰ卷)南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔148.5 m时,相应水面的面积为140.0 km2;水位为海拔157.5 m时,相应水面的面积为180.0 km2,将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔148.5 m上升到157.5 m时,增加的水量约为(≈2.65)( )
A.1.0×109 m3 B.1.2×109 m3
C.1.4×109 m3 D.1.6×109 m3
5.(2021·全国乙卷)在正方体ABCD-A1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为( )
A. B. C. D.
6.如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α,β所成的角分别为和.过A,B分别作两平面交线的垂线,垂足为A′,B′,则AB∶A′B′等于( )
A.2∶1 B.3∶1 C.3∶2 D.4∶3
7.底面半径为,母线长为2的圆锥的外接球O的表面积为( )
A.6π B.12π C.8π D.16π
8.(2022·广东韶关期末)在棱长为2的正方体ABCD-A1B1C1D1中,E是棱B1C1的中点,则过B、E、D1三点的平面截正方体所得的截面图形的面积为( )
A.5 B. C.2 D.4
二、选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.如图是一个正方体的平面展开图,在这个正方体中,以下四个命题中,正确的是( )
A.BM∥ED
B.EF∥CD
C.CN与BM为异面直线
D.DM⊥BN
10.(2022·新高考Ⅱ卷)如图,四边形ABCD为正方形,ED⊥平面ABCD,FB∥ED,AB=ED=2FB,记三棱锥E-ABC,F-ABC,E-ACF的体积分别为V1,V2,V3,则( )
A.V3=2V2 B.V3=V1
C.V3=V1+V2 D.2V3=3V1
11.如图是四棱锥的平面展开图,其中四边形ABCD为正方形,E,F,G,H分别为PA,PD,PC,PB的中点,在此几何体中,给出下面四个结论,其中正确的有( )
A.平面EFGH∥平面ABCD
B.BC∥平面PAD
C.AB∥平面PCD
D.平面PAD∥平面PAB
12.如图,已知长方体ABCD-A1B1C1D1中,四边形ABCD为正方形,AB=2,AA1=,E,F分别为AB,BC的中点.则( )
A.A1E⊥DF
B.点A1、E、F、C1四点共面
C.直线C1D与平面BB1C1C所成角的正切值为
D.三棱锥E-C1DF的体积为
三、填空题(本大题共4小题,每小题5分,共20分)
13.如果用半径R=2的半圆形铁皮卷成一个圆锥筒,那么这个圆锥筒的高是 .
14.如图,在三棱柱A1B1C1-ABC中,D,E,F分别是AB,AC,AA1的中点,设三棱锥F-ADE的体积为V1,三棱柱A1B1C1-ABC的体积为V2,则V1∶V2= .
15.如图,若边长为4和3与边长为4和2的两个矩形所在的平面互相垂直,则cos α∶cos β= .
16.已知一个球与一个正三棱柱的三个侧面和两个底面都相切,且这个球的体积是那么这个三棱柱的侧面积为 ,体积是 .
四、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,其高为6 cm,底面三角形的边长分别为3 cm,4 cm,5 cm,以上、下底面的内切圆为底面,挖去一个圆柱,求剩余部分几何体的体积V.
18.(本小题满分12分)如图,空间四边形ABCD中,E,F分别是AB和BC上的点,G,H分别是CD和AD上的点.
(1)如图①,若EH与FG相交于点K,求证:EH,BD,FG三条直线相交于同一点;
(2)如图②,若EH∥FG,求证:EH,BD,FG三条直线互相平行.
19.(本小题满分12分)如图,在四棱锥P-ABCD中,底面ABCD是菱形,且PB=PD.
(1)求证:BD⊥PC;
(2)若平面PBC与平面PAD的交线为l,求证:BC∥l.
20.(本小题满分12分)(2022·江西临川一中期中)如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,D为棱BC的中点.
(1)证明:A1C∥平面AB1D;
(2)求点A1到平面AB1D的距离.
21.(本小题满分12分)如图①,在矩形ABCD中,AD=1,AB=3,M为CD上一点,且CM=2MD.将△ADM沿AM折起,使得平面ADM⊥平面ABCM,如图②,点E是线段AM的中点.
(1)求证:平面BDE⊥平面ABCM;
(2)过B点是否存在一条直线l,同时满足以下两个条件:①l 平面ABCM;②l⊥AD.请说明理由.
22.(本小题满分12分)(2022·贵州月考)在我国古代数学名著《九章算术》中将由四个直角三角形组成的四面体称为“鳖臑(nào)”.如图,在三棱锥P-ABC中,PA⊥平面ABC,PA=BC=,AB=1,AC=2,E为棱PB上一点.
(1)若AE⊥平面PBC,求VP-ACE∶VE-ABC;
(2)求二面角A-PC-B的余弦值.
章末综合测评(三) 立体几何初步
1.C [对于A,空间任意三点,当三点共线时能确定一条直线而不是平面,故错误;对于B,空间两条直线,当两条直线重合时,过这条直线的平面有无数个,故错误;对于C,空间两条相交直线,根据课本中的判定得到是正确的;对于D,一条直线和一个点,当这个点在直线上时,过这条直线的平面有无数个,故错误.故选C.]
2.C [棱柱的侧面积S侧=3×6×4=72(cm2).]
3.B [平行四边形O′A′B′C′中,O′A′=5,O′C′=2,∠A′O′C′=30°,所以平行四边形O′A′B′C′的面积为S′=O′A′·O′C′·sin 30°=5×2×=5,所以原平面图形的面积是S=2S′=2=.故选B.]
4.C [依题意可知棱台的高为MN=157.5-148.5=9(m),所以增加的水量即为棱台的体积V.
棱台下底面积S=140.0 km2=140×106m2,上底面积S′=180.0 km2=180×106m2,
∴V=h=×9×=3××106≈(96+18×2.65)×107=1.437×109≈1.4×109(m3).
故选C.]
5.D [法一:如图,连接C1P,因为ABCD-A1B1C1D1是正方体,
且P为B1D1的中点,所以C1P⊥B1D1,又C1P⊥BB1,所以C1P⊥平面B1BP.又BP 平面B1BP,所以C1P⊥BP.连接BC1,则AD1∥BC1,所以∠PBC1为直线PB与AD1所成的角.设正方体ABCD-A1B1C1D1的棱长为2,则在直角三角形C1PB中,C1P=,所以∠PBC1=,故选D.
法二:如图所示,连接BC1,A1B,A1P,PC1,则易知AD1∥BC1,所以直线PB与AD1所成角等于直线PB与BC1所成角.根据P为正方形A1B1C1D1的对角线B1D1的中点,易知A1,P,C1三点共线,且P为A1C1的中点.易知A1B=BC1=A1C1,所以△A1BC1为等边三角形,所以∠A1BC1=,又P为A1C1的中点,所以可得∠PBC1=∠A1BC1=.]
6.A [连接AB′,A′B(图略),由已知条件可知∠BAB′=,∠ABA′=,
设AB=2a,则BB′=2a sin a,
A′B=2a cos a,
∴在Rt△BB′A′中,得A′B′=a,
∴AB∶A′B′=2∶1.]
7.D [由题意,圆锥轴截面的顶角为120°,设该圆锥的底面圆心为O′,球O的半径为R,则O′O=R-1.
由勾股定理可得R2=(R-1)2+2,∴R=2,
∴球O的表面积为4πR2=16π.]
8.C [设平面BED1交棱AD于F,由正方体性质及平面与平面平行的性质定理得ED1∥BF,D1F∥BE,
由勾股定理可得四边形D1FBE所有边长的长度为,
所以D1FBE是菱形,且F为AD的中点,
取A1D1的中点M,连接FM,ME,
则D1B=
=,
EF=,
故=.故选C.]
9.BCD [作出正方体的直观图,如图,由直观图可知BM与DE为互相垂直的异面直线,故A错误;EF∥AB∥CD,故B正确;
CN与BM为异面直线,故C正确;
由正方体性质得BN⊥平面DEM,故NB⊥DM,故D正确.故选BCD.]
10.CD [设AB=ED=2FB=2,则V1===.连接BD交AC于M,连接EM、FM(图略),则FM=,EF=3,所以FM 2+EM 2=EF 2,∴EM⊥FM,故S△EMF=S△EMF×AC=2,V3=V1+V2,2V3=3V1,故选CD.]
11.ABC [把平面展开图还原为四棱锥如图所示,则EH∥AB,因为AB 平面ABCD,EH 平面ABCD,所以EH∥平面ABCD.同理可证EF∥平面ABCD,因为EH∩EF=E,EH,EF 平面EFGH,所以平面EFGH∥平面ABCD;平面PAD,平面PBC,平面PAB,平面PDC均是四棱锥的四个侧面,则它们两两相交.因为AB∥CD,CD 平面PCD,AB 平面PCD,所以AB∥平面PCD.同理,BC∥平面PAD.]
12.BCD [对于A,假设A1E⊥DF,由题意知BC⊥平面AA1B1B,A1E 平面AA1B1B,∴A1E⊥BC,又BC∩DF=F,∴A1E⊥平面ABCD,由长方体性质知A1E与平面ABCD不垂直,故假设不成立,故A错误;
对于B,连接EF,AC,A1C1,由于E,F分别为AB,BC的中点,∴EF∥AC,又因为长方体ABCD-A1B1C1D1,知A1C1∥AC,∴EF∥A1C1,所以点A1、E、F、C1四点共面,故B正确;
对于C,由题意可知DC⊥平面BB1C1C,∴∠DC1C为直线C1D与平面BB1C1C所成角,在Rt△DCC1中,CC1=,CD=2,则tan∠DC1C=,故C正确;
对于D,连接DE,C1E,∵AB=AD=2,则S△DEF=S□ABCD-S△ADE-S△BEF-S△CDF=2×2-利用等体积法知:==·S△DEF·CC1=,故D正确.故选BCD.]
13.3 [设圆锥筒的底面半径为r,则2πr=πR=2π,则r=,
所以圆锥筒的高h==3.]
14.1∶24 [因为D,E分别是AB,AC的中点,
所以S△ADE∶S△ABC=1∶4.又F是AA1的中点,
所以A1到底面的距离H为F到底面距离h的2倍,即三棱柱A1B1C1-ABC的高是三棱锥F-ADE高的2倍,所以V1∶V2==1∶24.]
15.∶2 [如图,设两个矩形分别为矩形ABCD、矩形ABEF,因为平面ABCD⊥平面ABEF,
平面ABCD∩平面ABEF=AB,
AF 平面ABEF,AF⊥AB,故AF⊥平面ABCD,而AC 平面ABCD,
所以AF⊥AC,同理CB⊥BF.
由题意,两个矩形的对角线长分别为5,2,
所以cos α=,cos β=,
所以cos α∶cos β=∶2.]
16.48 48 [设球的半径为r,则πr3=π,
得r=2,柱体的高为2r=4.
又正三棱柱的底面三角形的内切圆半径与球的半径相等,
所以底面正三角形的边长为4,
所以正三棱柱的侧面积S侧=3×4×4,
体积V=2×4=48.]
17.解:×3×4×6=36(cm3).
设圆柱底面圆的半径为r,则r===1,
=πr2h=6π(cm3).
所以V=-=(36-6π)cm3.
18.证明:(1)因为K∈EH,EH 平面ABD,
所以K∈平面ABD,同理K∈平面CBD,而平面ABD∩平面CBD=BD,因此K∈BD,
所以EH,BD,FG三条直线相交于同一点.
(2)因为EH∥FG,FG 平面BCD,EH 平面BCD,
所以EH∥平面BCD,而EH 平面ABD,平面ABD∩平面BCD=BD,
所以EH∥BD,而EH∥FG,所以EH∥FG∥BD.
19.证明:(1)如图,连接AC,交BD于点O,连接PO.
因为四边形ABCD为菱形,所以BD⊥AC.
又因为PB=PD,O为BD的中点,
所以BD⊥PO.
因为PO∩AC=O,所以BD⊥平面PAC,
因为PC 平面PAC,所以BD⊥PC.
(2)因为四边形ABCD为菱形,所以BC∥AD.
因为BC 平面PAD,AD 平面PAD,
所以BC∥平面PAD.
又因为BC 平面PBC,
平面PBC与平面PAD的交线为l,所以BC∥l.
20.解:(1)证明:连接A1B交AB1于O,连接OD,
正三棱柱ABC-A1B1C1中,易得O为AB1中点,
又D为BC的中点,所以OD∥A1C.
因为A1C 平面AB1D,OD 平面AB1D,
所以A1C∥平面AB1D.
(2)因为A1C∥平面AB1D,
所以C与A1到平面AB1D的距离相等,
由题意得AB1=2,
因为AD2+=,所以AD⊥DB1,
所以,S△ADC=,
设C到平面ADB1的距离为h,则,
所以×2,所以h=,
即点A1到平面AB1D的距离为.
21.解:(1)证明:由已知得DA=DM,E是AM的中点,所以DE⊥AM.
因为平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,所以DE⊥平面ABCM.
又DE 平面BDE,所以平面BDE⊥平面ABCM.
(2)过B点存在一条直线l,同时满足以下两个条件:①l 平面ABCM;②l⊥AD.
理由:
在平面ABCM中,
过点B作直线l,使l⊥AM(图略).
因为平面ADM⊥平面ABCM,平面ABCM∩平面ADM=AM,所以l⊥平面ADM,所以l⊥AD.
22.解:(1)因PA⊥平面ABC,BC 平面ABC,AB 平面ABC,则PA⊥BC,PA⊥AB,又AB2+BC2=AC2,即AB⊥BC.又PA∩AB=A,PA,AB 平面PAB,因此BC⊥平面PAB.
所以VP-ACE∶VE-ABC=VC-PAE∶VC-ABE=PE∶EB,
在Rt△PAB中,PB=2,由AE⊥平面PBC得AE⊥PB,则PA·AB=PB·AE,即有AE=,
在Rt△PAE中,PE=,则有EB=,所以VP-ACE∶VE-ABC=3∶1.
(2)如图,作AE⊥PB于点E,过点E作EO垂直PC于点O,连接AO.
由(1)知,BC⊥平面PAB,AE 平面PAB,则BC⊥AE,而PB∩BC=B,PB,BC 平面PBC,
于是得AE⊥平面PBC.
又PC 平面PBC,则AE⊥PC.
又EO⊥PC,AE,EO 平面AOE,AE∩EO=E,
则有PC⊥平面AOE,所以PC⊥AO.
因此∠AOE是二面角A-PC-B的平面角.
在Rt△PAC中,PC=,
则AO=.
由(1)知,AE=,
在Rt△AOE中,sin ∠AOE=,
则cos ∠AOE=,
所以二面角A-PC-B的余弦值是.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
