8.1 成对数据的统计相关性 学案(含答案)-2024春高中数学选择性必修3(人教版)
文档属性
| 名称 | 8.1 成对数据的统计相关性 学案(含答案)-2024春高中数学选择性必修3(人教版) |

|
|
| 格式 | docx | ||
| 文件大小 | 373.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-13 16:32:30 | ||
图片预览




文档简介
第八章 成对数据的统计分析
[学习目标]
1.会通过收集现实问题中两个有关联变量的数据作出散点图,能利用散点图直观认识变量间的相关关系.
2.会求样本相关系数r,并能利用样本相关系数r判断两个随机变量线性相关程度的大小.
一、相关关系的概念
问题1 下列两个变量是否具有函数关系?
(1)球的面积与半径的关系;
(2)人的身高和体重的关系;
(3)角度和它的余弦值的关系;
(4)父母的身高和子女的身高的关系.
知识梳理
两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为________关系.
例1 (多选)下列两个变量存在相关关系的为( )
A.扇形的半径与面积之间的关系
B.降雪量与交通事故的发生率之间的关系
C.人的身高与体重之间的关系
D.家庭的支出与收入之间的关系
反思感悟 函数关系是一种确定的关系,而相关关系是非随机变量与随机变量的关系.函数关系是一种因果关系, 而相关关系不一定是因果关系,也可能是伴随关系.
跟踪训练1 (多选)下列说法正确的是( )
A.闯红灯与交通事故发生率的关系是相关关系
B.同一物体的加速度与作用力的关系是函数关系
C.产品的成本与产量的关系是函数关系
D.广告费用与销售量的关系是相关关系
二、散点图与变量的相关关系
知识梳理
1.散点图:为了更加直观地描述成对样本数据中两个变量之间的关系,用横轴表示其中的一个变量,纵轴表示另一个变量,则成对样本数据都可用直角坐标系中的点表示出来,由这些点组成的统计图叫做散点图.
2.从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现________的趋势,我们就称这两个变量________相关;当一个变量的值增加时,另一个变量的相应值呈现________的趋势,则称这两个变量________相关.
3.一般地,如果两个变量的取值呈现正相关或负相关,而且散点落在____________附近,我们就称这两个变量________相关.
4.一般地,如果两个变量具有相关性,但不是线性相关,那么我们就称这两个变量非线性相关或曲线相关.
例2 某个男孩的年龄与身高的统计数据如表所示:
年龄x(岁) 1 2 3 4 5 6
身高y(cm) 78 87 98 108 115 120
(1)画出散点图;
(2)判断y与x是否具有线性相关关系,如果相关,是正相关还是负相关?
反思感悟 判断两个变量x和y是否具有线性相关关系,常用的简便方法就是绘制散点图,如果发现点的分布从整体上看大致在一条直线附近,那么这两个变量就是线性相关的,注意不要受个别点的位置的影响.
跟踪训练2 下面是水稻产量与施化肥量的一组观测数据:
施化肥量 15 20 25 30 35 40 45
水稻产量 320 330 360 410 460 470 480
(1)将上述数据制成散点图;
(2)你能从散点图中发现施化肥量与水稻产量存在什么关系吗?水稻产量会一直随施化肥量的增加而增加吗?
三、样本相关系数
问题2 设x1,x2,…, xn和y1,y2,…,yn的均值分别为和.将每个变量的观测数据减去其均值,得到成对数据为(x1-,y1-),(x2-,y2-),…,(xn-,yn-),并绘制散点图,则绘制的散点图有什么特征?你能利用正负相关变量的成对样本数据平移后呈现的规律,构造一个度量成对样本数据是正相关还是负相关的数字特征吗?
问题3 你认为Lxy的大小一定能度量出成对样本数据的相关程度吗?
知识梳理
1.样本相关系数:
2.样本相关系数r的取值范围为__________.
当|r|越接近1时,成对样本数据的线性相关程度越______;
当|r|越接近0时,成对样本数据的线性相关程度越______.
例3 对四组成对样本数据进行统计,获得以下散点图,关于其样本相关系数的比较,正确的是( )
A.r2B.r4C.r4D.r2反思感悟 线性相关程度强弱的判断方法
(1)散点图:散点图只是粗略作出判断,其图象越接近直线,相关程度越强.
(2)样本相关系数:样本相关系数能够较准确的判断相关的程度,其绝对值越大,相关程度越强.
跟踪训练3 已知r1表示变量X与Y之间的样本相关系数,r2表示变量U与V之间的样本相关系数,且r1=0.837,r2=-0.957,则( )
A.变量X与Y之间呈正相关关系,且X与Y之间的相关程度强于U与V之间的相关程度
B.变量X与Y之间呈负相关关系,且X与Y之间的相关程度强于U与V之间的相关程度
C.变量U与V之间呈负相关关系,且X与Y之间的相关程度弱于U与V之间的相关程度
D.变量U与V之间呈正相关关系,且X与Y之间的相关程度弱于U与V之间的相关程度
四、样本相关系数的实际应用
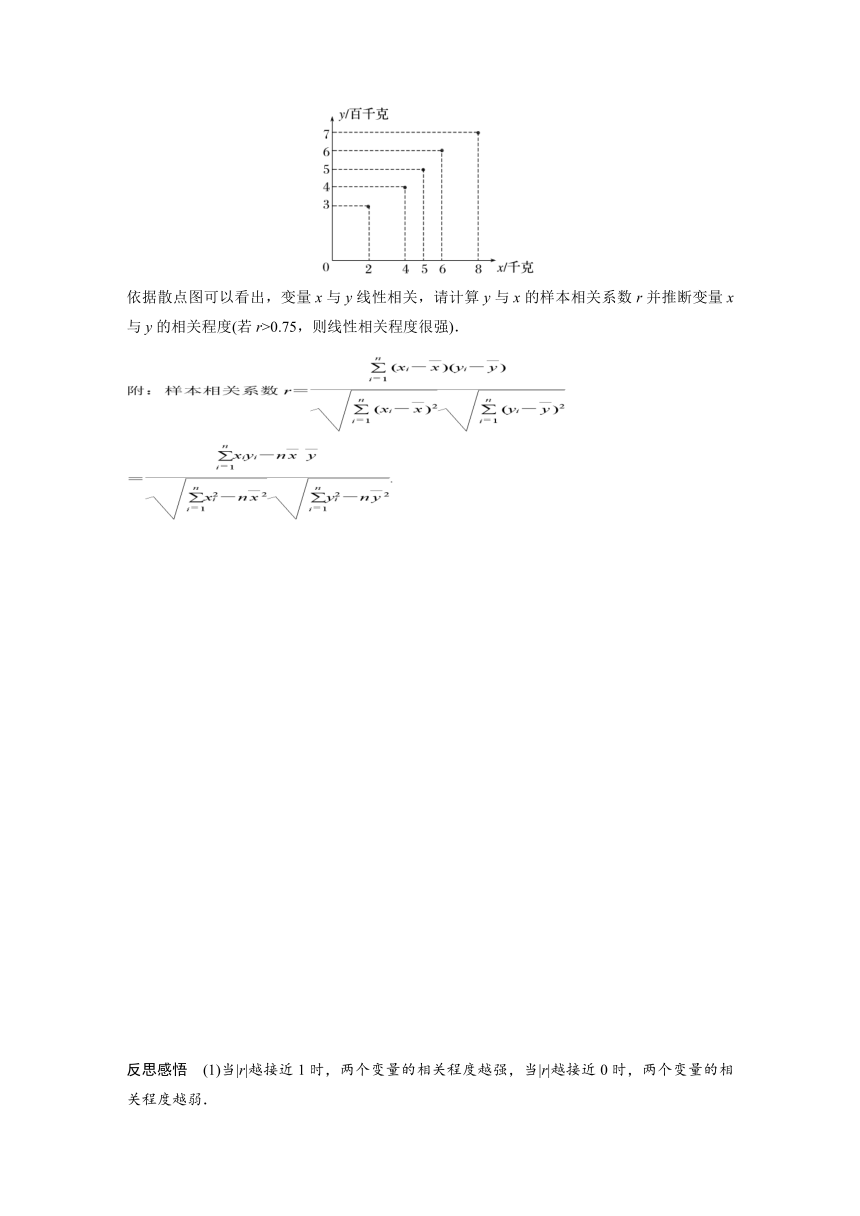
例4 根据统计,某蔬菜基地西红柿亩产量的增加量y(百千克)与某种液体肥料每亩使用量x(千克)之间的对应数据的散点图如图所示.
依据散点图可以看出,变量x与y线性相关,请计算y与x的样本相关系数r并推断变量x与y的相关程度(若r>0.75,则线性相关程度很强).
反思感悟 (1)当|r|越接近1时,两个变量的相关程度越强,当|r|越接近0时,两个变量的相关程度越弱.
(2)样本相关系数r有时也称样本线性相关系数,|r|刻画了样本点集中于某条直线的程度.当r=0时,只表明成对数据间没有线性相关关系,但不排除它们之间有其他相关关系.
跟踪训练4 为了监控某种零件的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个零件的尺寸:
抽取次序 1 2 3 4 5 6 7 8
零件尺寸 9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04
抽取次序 9 10 11 12 13 14 15 16
零件尺寸 10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95
求的样本相关系数r,并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小(若<0.25,则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小).(结果精确到0.01)
附:样本(xi,yi)(i=1,2,…,n)的样本相关系数
1.知识清单:
(1)相关关系的概念.
(2)散点图与变量的相关关系.
(3)样本相关系数及其实际应用.
2.方法归纳:数形结合.
3.常见误区:样本相关系数绝对值的大小与相关程度的关系.
1.下列两个变量存在相关关系的是( )
A.利息与利率
B.居民收入与储蓄存款
C.电视机产量与苹果产量
D.某种商品的销售额与销售价格
2.某商场五天内某种T恤衫的销售情况如表:
第x天 1 2 3 4 5
销售量y(件) 19 39 59 79 104
则下列说法正确的是( )
A.y与x负线性相关
B.y与x正线性相关
C.y与x不相关
D.y与x成正比例关系
3.(多选)下面各图中,散点图与样本相关系数r符合的是( )
§8.1 成对数据的统计相关性
问题1 (1)(3)是函数关系;(2)(4)不是函数关系.
知识梳理
相关
例1 BCD [扇形的半径与面积之间的关系是函数关系,其余均为相关关系.]
跟踪训练1 ABD [闯红灯与发生交通事故之间不是因果关系,但具有相关性,是相关关系,所以A正确;物体的加速度与作用力的关系是函数关系,所以B正确;产品的成本与产量之间是相关关系,所以C错误;广告费用与销售量之间是相关关系,所以D正确.]
知识梳理
2.增加 正 减小 负
3.一条直线 线性
例2 解 (1)散点图如图所示.
(2)由散点图知,所有散点分布在一条直线附近,因此,认为y与x具有线性相关关系,且是正相关关系.
跟踪训练2 解 (1)散点图如图.
(2)从图中可以发现,当施化肥量由小到大变化时,水稻产量也由小变大,图中的散点大致分布在一条直线的附近,因此施化肥量和水稻产量线性相关,但水稻产量只是在一定范围内随着施化肥量的增加而增加,不会一直随施化肥量的增加而增加.
问题2 散点图(略),发现正相关时散点大多数分布在第一象限、第三象限,负相关时散点大多数分布在第二象限、第四象限.构造一个量:
Lxy=[(x1-)(y1-)+(x2-)(y2-)+…+(xn-)·(yn-)].
一般情形下,Lxy>0表明成对样本数据正相关;Lxy<0表明成对样本数据负相关.
问题3 不一定.因为Lxy的大小与数据的度量单位有关,所以不宜直接用它度量成对样本数据相关程度的大小.
知识梳理
2.[-1,1] 强 弱
例3 A [由给出的四组成对样本数据的散点图可以看出,题图1和题图3是正相关,样本相关系数大于0,题图2和题图4是负相关,样本相关系数小于0,题图1和题图2的样本点集中在一条直线附近,所以相关程度更强,所以r1接近于1,r2接近于-1,由此可得r2跟踪训练3 C [因为r1=0.837>0,r2=-0.957<0,所以变量X与Y之间呈正相关关系,变量U与V之间呈负相关关系,因为|r1|<|r2|,所以X与Y之间的相关程度弱于U与V之间的相关程度.]
例4 解 由所给数据可得==5,
==5,
∵r===>0.75.
∴变量x与y的线性相关程度很强.
跟踪训练4 解 =×(1+2+3+…+16)=8.5,由样本数据得(xi,i)(i=1,2,…,16)的样本相关系数为r≈≈-0.18.
由于|r|<0.25,因此可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小.
随堂演练
1.B [选项A中的两个变量具有函数关系;选项B中居民收入与储蓄存款具有相关关系,一般来说,居民收入越高对应的储蓄存款越多;选项C中的电视机产量与苹果产量无任何关系;选项D中某种商品的销售额与销售价格具有函数关系.]
2.B [根据表格中的数据作出散点图如图,
可知所有点分布在一条直线附近,所以y与x是线性相关的,又y值随着x值的增大而增大,所以y与x正相关.]
3.ACD [因为样本相关系数r的绝对值越接近1,线性相关程度越强,且r>0时正相关,r<0时负相关,故观察各选项,易知B不符合,A,C,D均符合.]
4.0.849
[学习目标]
1.会通过收集现实问题中两个有关联变量的数据作出散点图,能利用散点图直观认识变量间的相关关系.
2.会求样本相关系数r,并能利用样本相关系数r判断两个随机变量线性相关程度的大小.
一、相关关系的概念
问题1 下列两个变量是否具有函数关系?
(1)球的面积与半径的关系;
(2)人的身高和体重的关系;
(3)角度和它的余弦值的关系;
(4)父母的身高和子女的身高的关系.
知识梳理
两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为________关系.
例1 (多选)下列两个变量存在相关关系的为( )
A.扇形的半径与面积之间的关系
B.降雪量与交通事故的发生率之间的关系
C.人的身高与体重之间的关系
D.家庭的支出与收入之间的关系
反思感悟 函数关系是一种确定的关系,而相关关系是非随机变量与随机变量的关系.函数关系是一种因果关系, 而相关关系不一定是因果关系,也可能是伴随关系.
跟踪训练1 (多选)下列说法正确的是( )
A.闯红灯与交通事故发生率的关系是相关关系
B.同一物体的加速度与作用力的关系是函数关系
C.产品的成本与产量的关系是函数关系
D.广告费用与销售量的关系是相关关系
二、散点图与变量的相关关系
知识梳理
1.散点图:为了更加直观地描述成对样本数据中两个变量之间的关系,用横轴表示其中的一个变量,纵轴表示另一个变量,则成对样本数据都可用直角坐标系中的点表示出来,由这些点组成的统计图叫做散点图.
2.从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现________的趋势,我们就称这两个变量________相关;当一个变量的值增加时,另一个变量的相应值呈现________的趋势,则称这两个变量________相关.
3.一般地,如果两个变量的取值呈现正相关或负相关,而且散点落在____________附近,我们就称这两个变量________相关.
4.一般地,如果两个变量具有相关性,但不是线性相关,那么我们就称这两个变量非线性相关或曲线相关.
例2 某个男孩的年龄与身高的统计数据如表所示:
年龄x(岁) 1 2 3 4 5 6
身高y(cm) 78 87 98 108 115 120
(1)画出散点图;
(2)判断y与x是否具有线性相关关系,如果相关,是正相关还是负相关?
反思感悟 判断两个变量x和y是否具有线性相关关系,常用的简便方法就是绘制散点图,如果发现点的分布从整体上看大致在一条直线附近,那么这两个变量就是线性相关的,注意不要受个别点的位置的影响.
跟踪训练2 下面是水稻产量与施化肥量的一组观测数据:
施化肥量 15 20 25 30 35 40 45
水稻产量 320 330 360 410 460 470 480
(1)将上述数据制成散点图;
(2)你能从散点图中发现施化肥量与水稻产量存在什么关系吗?水稻产量会一直随施化肥量的增加而增加吗?
三、样本相关系数
问题2 设x1,x2,…, xn和y1,y2,…,yn的均值分别为和.将每个变量的观测数据减去其均值,得到成对数据为(x1-,y1-),(x2-,y2-),…,(xn-,yn-),并绘制散点图,则绘制的散点图有什么特征?你能利用正负相关变量的成对样本数据平移后呈现的规律,构造一个度量成对样本数据是正相关还是负相关的数字特征吗?
问题3 你认为Lxy的大小一定能度量出成对样本数据的相关程度吗?
知识梳理
1.样本相关系数:
2.样本相关系数r的取值范围为__________.
当|r|越接近1时,成对样本数据的线性相关程度越______;
当|r|越接近0时,成对样本数据的线性相关程度越______.
例3 对四组成对样本数据进行统计,获得以下散点图,关于其样本相关系数的比较,正确的是( )
A.r2
(1)散点图:散点图只是粗略作出判断,其图象越接近直线,相关程度越强.
(2)样本相关系数:样本相关系数能够较准确的判断相关的程度,其绝对值越大,相关程度越强.
跟踪训练3 已知r1表示变量X与Y之间的样本相关系数,r2表示变量U与V之间的样本相关系数,且r1=0.837,r2=-0.957,则( )
A.变量X与Y之间呈正相关关系,且X与Y之间的相关程度强于U与V之间的相关程度
B.变量X与Y之间呈负相关关系,且X与Y之间的相关程度强于U与V之间的相关程度
C.变量U与V之间呈负相关关系,且X与Y之间的相关程度弱于U与V之间的相关程度
D.变量U与V之间呈正相关关系,且X与Y之间的相关程度弱于U与V之间的相关程度
四、样本相关系数的实际应用
例4 根据统计,某蔬菜基地西红柿亩产量的增加量y(百千克)与某种液体肥料每亩使用量x(千克)之间的对应数据的散点图如图所示.
依据散点图可以看出,变量x与y线性相关,请计算y与x的样本相关系数r并推断变量x与y的相关程度(若r>0.75,则线性相关程度很强).
反思感悟 (1)当|r|越接近1时,两个变量的相关程度越强,当|r|越接近0时,两个变量的相关程度越弱.
(2)样本相关系数r有时也称样本线性相关系数,|r|刻画了样本点集中于某条直线的程度.当r=0时,只表明成对数据间没有线性相关关系,但不排除它们之间有其他相关关系.
跟踪训练4 为了监控某种零件的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个零件的尺寸:
抽取次序 1 2 3 4 5 6 7 8
零件尺寸 9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04
抽取次序 9 10 11 12 13 14 15 16
零件尺寸 10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95
求的样本相关系数r,并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小(若<0.25,则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小).(结果精确到0.01)
附:样本(xi,yi)(i=1,2,…,n)的样本相关系数
1.知识清单:
(1)相关关系的概念.
(2)散点图与变量的相关关系.
(3)样本相关系数及其实际应用.
2.方法归纳:数形结合.
3.常见误区:样本相关系数绝对值的大小与相关程度的关系.
1.下列两个变量存在相关关系的是( )
A.利息与利率
B.居民收入与储蓄存款
C.电视机产量与苹果产量
D.某种商品的销售额与销售价格
2.某商场五天内某种T恤衫的销售情况如表:
第x天 1 2 3 4 5
销售量y(件) 19 39 59 79 104
则下列说法正确的是( )
A.y与x负线性相关
B.y与x正线性相关
C.y与x不相关
D.y与x成正比例关系
3.(多选)下面各图中,散点图与样本相关系数r符合的是( )
§8.1 成对数据的统计相关性
问题1 (1)(3)是函数关系;(2)(4)不是函数关系.
知识梳理
相关
例1 BCD [扇形的半径与面积之间的关系是函数关系,其余均为相关关系.]
跟踪训练1 ABD [闯红灯与发生交通事故之间不是因果关系,但具有相关性,是相关关系,所以A正确;物体的加速度与作用力的关系是函数关系,所以B正确;产品的成本与产量之间是相关关系,所以C错误;广告费用与销售量之间是相关关系,所以D正确.]
知识梳理
2.增加 正 减小 负
3.一条直线 线性
例2 解 (1)散点图如图所示.
(2)由散点图知,所有散点分布在一条直线附近,因此,认为y与x具有线性相关关系,且是正相关关系.
跟踪训练2 解 (1)散点图如图.
(2)从图中可以发现,当施化肥量由小到大变化时,水稻产量也由小变大,图中的散点大致分布在一条直线的附近,因此施化肥量和水稻产量线性相关,但水稻产量只是在一定范围内随着施化肥量的增加而增加,不会一直随施化肥量的增加而增加.
问题2 散点图(略),发现正相关时散点大多数分布在第一象限、第三象限,负相关时散点大多数分布在第二象限、第四象限.构造一个量:
Lxy=[(x1-)(y1-)+(x2-)(y2-)+…+(xn-)·(yn-)].
一般情形下,Lxy>0表明成对样本数据正相关;Lxy<0表明成对样本数据负相关.
问题3 不一定.因为Lxy的大小与数据的度量单位有关,所以不宜直接用它度量成对样本数据相关程度的大小.
知识梳理
2.[-1,1] 强 弱
例3 A [由给出的四组成对样本数据的散点图可以看出,题图1和题图3是正相关,样本相关系数大于0,题图2和题图4是负相关,样本相关系数小于0,题图1和题图2的样本点集中在一条直线附近,所以相关程度更强,所以r1接近于1,r2接近于-1,由此可得r2
例4 解 由所给数据可得==5,
==5,
∵r===>0.75.
∴变量x与y的线性相关程度很强.
跟踪训练4 解 =×(1+2+3+…+16)=8.5,由样本数据得(xi,i)(i=1,2,…,16)的样本相关系数为r≈≈-0.18.
由于|r|<0.25,因此可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小.
随堂演练
1.B [选项A中的两个变量具有函数关系;选项B中居民收入与储蓄存款具有相关关系,一般来说,居民收入越高对应的储蓄存款越多;选项C中的电视机产量与苹果产量无任何关系;选项D中某种商品的销售额与销售价格具有函数关系.]
2.B [根据表格中的数据作出散点图如图,
可知所有点分布在一条直线附近,所以y与x是线性相关的,又y值随着x值的增大而增大,所以y与x正相关.]
3.ACD [因为样本相关系数r的绝对值越接近1,线性相关程度越强,且r>0时正相关,r<0时负相关,故观察各选项,易知B不符合,A,C,D均符合.]
4.0.849
