2024届高考物理二轮专题导学案:有界磁场的圆周运动(含答案)
文档属性
| 名称 | 2024届高考物理二轮专题导学案:有界磁场的圆周运动(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 692.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-03-13 13:40:16 | ||
图片预览


文档简介
有界磁场的圆周运动
总结归纳
1.确定圆心的方法: 2.求解半径的一般方法:
3.求解时间的一般方法: 4.经常涉及的角度关系:
5.组合场时涉及的运动形式:
典型例题
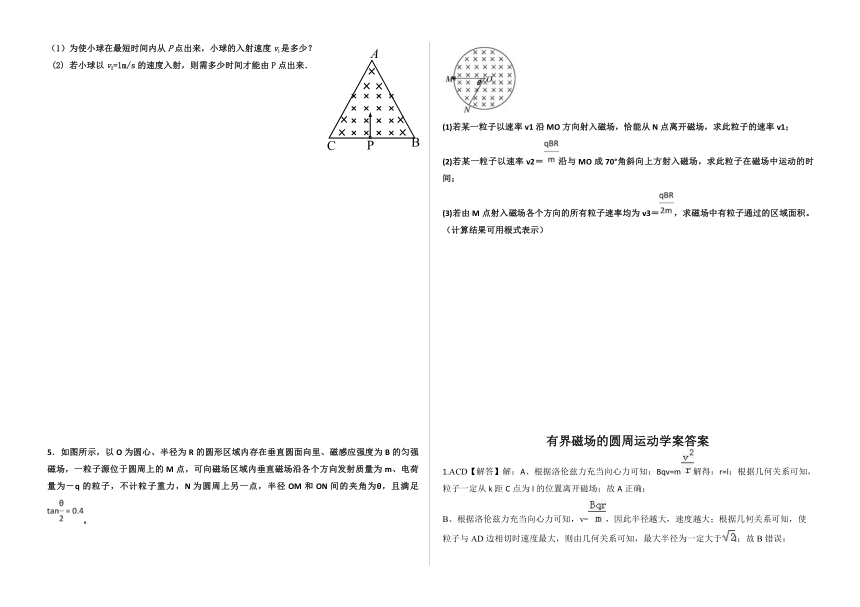
1.(多选题)如图所示,在一等腰直角三角形ACD区域内有垂直纸面向外的匀强磁场,磁场的磁感应强度大小为B.一质量为m、电荷量为q的带正电粒子(不计重力)从AC边的中点O垂直于AC边射入该匀强磁场区域,若该三角形的两直角边长均为2l,则下列关于粒子运动的说法中正确的是( )
A.若该粒子的入射速度为v=,则粒子一定从CD边射出磁场,且距点C的距离为l
B.若要使粒子从CD边射出,则该粒子从O点入射的最大速度应为v=
C.若要使粒子从AC边射出,则该粒子从O点入射的最大速度应为v=
D.该粒子以不同的速度入射时,在磁场中运动的最长时间为
2.(多选题)如图所示,S处有一电子源,可向纸面内任意方向发射电子,平板MN垂直于纸面,在纸面内的长度L=9.1cm,中点O与S间的距离d=4.55cm,MN与SO直线的夹角为θ,板所在平面有电子源的一侧区域有方向垂直于纸面向外的匀强磁场,磁感应强度B=2.0×10-4T,电子质量m=9.1×10-31kg,电量e=-1.6×10-19C,不计电子重力。电子源发射速度v=1.6×106m/s的一个电子,该电子打在板上可能位置的区域的长度为l,则
A.θ=90°时,l=9.1cm B.θ=90°时,l=4.55cm
C.θ=30°时,l=9.1cm D.θ=30°时,l=4.55cm
3、如图所示,在以坐标原点O为圆心、半径为R的半圆形区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B,磁场方向垂直于xOy平面向里。一带正电的粒子(不计重力)从O点沿y轴正方向以某一速度射入,带电粒子恰好做匀速直线运动,经t0时间从P点射出。
(1)求电场强度的大小和方向。
(2)当仅撤去磁场时,带电粒子仍从O点以相同的速度射入,经时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。
(3)当仅撤去电场时,带电粒子仍从O点射入,且速度为原来的4倍,求粒子在磁场中运动的时间。
4、 边长为100cm的正三角形光滑且绝缘的刚性框架ABC固定在光滑的水平面上,如下图内有垂直于框架平面B=0.5T的匀强磁场.一质量为 m=2×10-4kg,带电量为q=4×10-3C小球,从BC边的中点小孔P处以某一速度垂直于BC边射入磁场,设小球与框架相碰后不损失动能.求
(1)为使小球在最短时间内从P点出来,小球的入射速度v1是多少?
(2) 若小球以v2=1m/s的速度入射,则需多少时间才能由P点出来.
5.如图所示,以O为圆心、半径为R的圆形区域内存在垂直圆面向里、磁感应强度为B的匀强磁场,一粒子源位于圆周上的M点,可向磁场区域内垂直磁场沿各个方向发射质量为m、电荷量为-q的粒子,不计粒子重力,N为圆周上另一点,半径OM和ON间的夹角为θ,且满足。
(1)若某一粒子以速率v1沿MO方向射入磁场,恰能从N点离开磁场,求此粒子的速率v1;
(2)若某一粒子以速率v2=沿与MO成70°角斜向上方射入磁场,求此粒子在磁场中运动的时间;
(3)若由M点射入磁场各个方向的所有粒子速率均为v3=,求磁场中有粒子通过的区域面积。(计算结果可用根式表示)
有界磁场的圆周运动学案答案
1.ACD【解答】解:A、根据洛伦兹力充当向心力可知:Bqv=m解得:r=l;根据几何关系可知,粒子一定从k距C点为l的位置离开磁场;故A正确;
B、根据洛伦兹力充当向心力可知,v=,因此半径越大,速度越大;根据几何关系可知,使粒子与AD边相切时速度最大,则由几何关系可知,最大半径为一定大于l;故B错误;
C、若要使粒子从AC边射出,则该粒子从O点入射的最大半径为; 因此最大速度速度应为v=;故C正确;
D、粒子运行周期为,根据几何关系可知,粒子在磁场中最大圆心角为180°;故最长时间为;故D正确;
故选:ACD.
2.AD试题分析:电子在磁场中受洛伦兹力作用做匀速圆周运动,根据洛伦兹力大小计算公式和向心力公式有:evB=,解得电子圆周运动的轨道半径为:r==m=4.55×10-2m=4.55cm,恰好有:r=d=L/2,由于电子源S,可向纸面内任意方向发射电子,因此电子的运动轨迹将是过S点的一系列半径为r的等大圆,能够打到板MN上的区域范围如下图所示,实线SN表示电子刚好经过板N端时的轨迹,实线SA表示电子轨迹刚好与板相切于A点时的轨迹,因此电子打在板上可能位置的区域的长度为:l=NA,
3.
4.
5.
(1)如图所示,由几何关系可知,,解得:
粒子在磁场中做圆周运动,洛伦兹力提供向心力:,解得:
(2)粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,设轨迹半径为
洛伦兹力提供向心力:,得,其中,解得:
粒子沿与与MO成70°方向进入磁场,设粒子从区域边界P射出,其运动轨迹如图所示:
由图中几何关系可知粒子轨迹所对应的圆心角为α=160°
粒子运动周期:
则粒子在磁场中的运动的时间:
(3)粒子沿各个方向以进入磁场做匀速圆周时的轨迹半径都为,且不变,如图所示
由图可知,粒子在磁场中通过的面积等于以为圆心的扇形的面积、以M为圆心的扇形的面积和以O点为圆心的圆弧MQ与直线MQ围成的面积之和。
,,
所以:
自助作业
1.物理学家通过艰苦的实验来探究自然的物理规律,为人类的科学做出了巨大贡献,值得我
们敬仰,下列描述中符合物理学史实的是( )
A.开普勒发现了行星运动三定律,从而提出了日心学说
B.牛顿发现了万有引力定律但并未测定出引力常量G
C.奥斯特发现了电流的磁效应并提出了分子电流假说
D.法拉第发现了电磁感应现象并总结出了判断感应电流方向的规律
2.在如图所示电路中,电源电动势为E,内阻为r,电流表A、二极管和电压表V1、V2均为理
想电表,R1为定值电阻,R2为滑动变阻器。闭合开关S,当R2的滑动触头P向下滑动的过程中
( )
A.电压表V1的示数增大,电压表V2的示数减小
B.电压表V1示数的变化量的绝对值与电压表V2示数的变化量的绝对值相等
C.电容器上的电压与电流表A示数的比值不变
D.电压表V1示数的变化量与电流表A示数的变化量的比值保持不变
3.如图所示,一劲度系数为k的轻质弹簧,上端固定,下端连一质量为m的物块A,A放在质量也为m的托盘B上,以FN表示B对A的作用力,x表示弹簧的伸长量.初始时,在竖直向上的力F作用下系统静止,且弹簧处于自然状态(x=0).现改变力F的大小,使B以的加速度匀加速向下运动(g为重力加速度,空气阻力不计),此过程中FN或F随x变化的图象正确的是 ( )
4. 图中的变压器为理想变压器,原线圈匝数与副线圈匝数之比为10 ∶1,变压器的原线圈接如图所示的正弦式交流电,电阻和电容器连接成如图所示的电路,其中,电容器的击穿电压为8V,电压表V为理想交流电表,开关S处于断开状态,则下列说法正确的是( )
A.电压表V的读数约为5.07V
B.电流表A的读数为0.05A
C.电阻R2上消耗的功率为2.5W
D.若闭合开关S,电容器会被击穿
5.如图所示,一点电荷固定在光滑水平面上的O点,虚线a、b、c、d是点电荷激发电场的四条等距离的等势线。一个带电小滑块从等势线d上的1处以水平初速度v0运动,结果形成了实线所示的小滑块运动轨迹。1、2、3、4、5是等势线与小滑块运动轨迹的一些交点,由此可以判定错误的是( )
A.固定电荷与小滑块电性一定相同
B.在1、2、3、4、5五个位置上小滑块具有的动能与电势能之和一定相等
C.在整个过程中小滑块的加速度先变大后变小
D.小滑块从位置1到2和从位置3到4的过程中,电场力做功的大小关系是W12=3W34
6.如图所示,置于竖直面内的光滑金属圆环半径为r,质量为m的带孔小球穿于环上,同时有一长为r的细绳一端系于圆环最高点,当圆环以角速度绕竖直直径转动时, ( )
A.细绳对小球的拉力可能为零
B.细绳和金属圆环对小球的作用力大小可能相等
C.细绳对小球拉力与小球的重力大小不可能相等
D.当时,金属圆环对小球的作用力为零
7.如图所示,一个半径为R的导电圆环与一个轴向对称的发散磁场处处正交,环上各点的磁感应强度B大小相等,方向均与环面轴线方向成θ角(环面轴线为竖直方向)。若导线环上载有如图所示的恒定电流I,则下列说法正确的是( )
A. 导电圆环有收缩的趋势
B. 导电圆环所受安培力方向竖直向上
C. 导电圆环所受安培力的大小为2BIR
D. 导电圆环所受安培力的大小为3πBIRsinθ
8.如图所示,一轻绳吊着粗细均匀的棒,棒下端离地面高H,上端套着一个细环.棒和环的质量均为m,相互间最大静摩擦力等于滑动摩擦力,大小为kmg(k>1).断开轻绳,棒和环自由下落.假设棒足够长,与地面发生碰撞时,触地时间极短,无动能损失.棒在整个运动过程中始终保持竖直,空气阻力不计.则 ( )
A.从断开轻绳到棒和环都静止的过程中,环相对于棒有往复运动,但总位移向下
B.棒第一次与地面碰撞弹起上升过程中,棒和环都做匀减速运动
C.从断开轻绳到棒和环都静止的过程中,环相对于地面始终向下运动
D.从断开轻绳到棒和环都静止,摩擦力做的总功为-
9.(6分)将两根自然长度相同、劲度系数不同、粗细也不同的弹簧套在一起,看做一根新弹簧,设原粗弹簧(记为A)劲度系数为k1,原细弹簧(记为B)劲度系数为k2,套成的新弹簧(记为C)劲度系数为k3.关于k1、k2、k3的大小关系,同学们做出了如下猜想:
甲同学:和电阻并联相似,可能是=+
乙同学:和电阻串联相似,可能是k3=k1+k2
丙同学:可能是k3=
(1)为了验证猜想,同学们设计了相应的实验.(装置见图甲)
(2)简要实验步骤如下,请完成相应填空.
①将弹簧A悬挂在铁架台上,用刻度尺测量弹簧A的自然长度L0;
②在弹簧A的下端挂上钩码,记下钩码的个数n、每个钩码的质量m和当地的重力加速度大小g,并用刻度尺测量弹簧的长度L1;
③由F=____计算弹簧的弹力,由x=L1-L0计算弹簧的伸长量,由k=计算弹簧的劲度系数;
④改变____,重复实验步骤②、③,并求出弹簧A的劲度系数的平均值k1;
⑤仅将弹簧分别换为B、C,重复上述操作步骤,求出弹簧B、C的劲度系数的平均值k2、k3.比较k1、k2、k3并得出结论.
(3)图乙是实验得到的图线,由此可以判断____同学的猜想正确.
10.(10分)电压表改装前需要测量其内阻,测量电压表内阻的电路如图甲,所用电源为内阻可以忽略的干电池,定值电阻R1=8 000 Ω,R2=4 000 Ω.
(1)闭合S1,断开S2,调节电阻箱R,记下多组R的大小及其对应的电压表示数U;
(2)闭合S1,____,同样调节电阻箱R,记下多组R的大小及其对应的电压表示数U;将以上两次测得的多组数据,分别在坐标纸上描点连线,得到如图乙中所示两条图线;
(3)利用图线数据得出电源电动势E=____,求出电压表内阻Rv=____.两图线的交点的横坐标设为R0,还可用物理量符号R0、R1、R2表示Rv= .判断断开S2时,所得数据描绘的是图线____.(选填“AB”或“CD”)
自助作业参考答案:
1-8: B D D C D CD AB BCD
9.(6分)③nmg ④钩码的个数 (3)乙
10.(10分)(2)闭合S2 (3)3.0 V 5000 Ω AB
总结归纳
1.确定圆心的方法: 2.求解半径的一般方法:
3.求解时间的一般方法: 4.经常涉及的角度关系:
5.组合场时涉及的运动形式:
典型例题
1.(多选题)如图所示,在一等腰直角三角形ACD区域内有垂直纸面向外的匀强磁场,磁场的磁感应强度大小为B.一质量为m、电荷量为q的带正电粒子(不计重力)从AC边的中点O垂直于AC边射入该匀强磁场区域,若该三角形的两直角边长均为2l,则下列关于粒子运动的说法中正确的是( )
A.若该粒子的入射速度为v=,则粒子一定从CD边射出磁场,且距点C的距离为l
B.若要使粒子从CD边射出,则该粒子从O点入射的最大速度应为v=
C.若要使粒子从AC边射出,则该粒子从O点入射的最大速度应为v=
D.该粒子以不同的速度入射时,在磁场中运动的最长时间为
2.(多选题)如图所示,S处有一电子源,可向纸面内任意方向发射电子,平板MN垂直于纸面,在纸面内的长度L=9.1cm,中点O与S间的距离d=4.55cm,MN与SO直线的夹角为θ,板所在平面有电子源的一侧区域有方向垂直于纸面向外的匀强磁场,磁感应强度B=2.0×10-4T,电子质量m=9.1×10-31kg,电量e=-1.6×10-19C,不计电子重力。电子源发射速度v=1.6×106m/s的一个电子,该电子打在板上可能位置的区域的长度为l,则
A.θ=90°时,l=9.1cm B.θ=90°时,l=4.55cm
C.θ=30°时,l=9.1cm D.θ=30°时,l=4.55cm
3、如图所示,在以坐标原点O为圆心、半径为R的半圆形区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B,磁场方向垂直于xOy平面向里。一带正电的粒子(不计重力)从O点沿y轴正方向以某一速度射入,带电粒子恰好做匀速直线运动,经t0时间从P点射出。
(1)求电场强度的大小和方向。
(2)当仅撤去磁场时,带电粒子仍从O点以相同的速度射入,经时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。
(3)当仅撤去电场时,带电粒子仍从O点射入,且速度为原来的4倍,求粒子在磁场中运动的时间。
4、 边长为100cm的正三角形光滑且绝缘的刚性框架ABC固定在光滑的水平面上,如下图内有垂直于框架平面B=0.5T的匀强磁场.一质量为 m=2×10-4kg,带电量为q=4×10-3C小球,从BC边的中点小孔P处以某一速度垂直于BC边射入磁场,设小球与框架相碰后不损失动能.求
(1)为使小球在最短时间内从P点出来,小球的入射速度v1是多少?
(2) 若小球以v2=1m/s的速度入射,则需多少时间才能由P点出来.
5.如图所示,以O为圆心、半径为R的圆形区域内存在垂直圆面向里、磁感应强度为B的匀强磁场,一粒子源位于圆周上的M点,可向磁场区域内垂直磁场沿各个方向发射质量为m、电荷量为-q的粒子,不计粒子重力,N为圆周上另一点,半径OM和ON间的夹角为θ,且满足。
(1)若某一粒子以速率v1沿MO方向射入磁场,恰能从N点离开磁场,求此粒子的速率v1;
(2)若某一粒子以速率v2=沿与MO成70°角斜向上方射入磁场,求此粒子在磁场中运动的时间;
(3)若由M点射入磁场各个方向的所有粒子速率均为v3=,求磁场中有粒子通过的区域面积。(计算结果可用根式表示)
有界磁场的圆周运动学案答案
1.ACD【解答】解:A、根据洛伦兹力充当向心力可知:Bqv=m解得:r=l;根据几何关系可知,粒子一定从k距C点为l的位置离开磁场;故A正确;
B、根据洛伦兹力充当向心力可知,v=,因此半径越大,速度越大;根据几何关系可知,使粒子与AD边相切时速度最大,则由几何关系可知,最大半径为一定大于l;故B错误;
C、若要使粒子从AC边射出,则该粒子从O点入射的最大半径为; 因此最大速度速度应为v=;故C正确;
D、粒子运行周期为,根据几何关系可知,粒子在磁场中最大圆心角为180°;故最长时间为;故D正确;
故选:ACD.
2.AD试题分析:电子在磁场中受洛伦兹力作用做匀速圆周运动,根据洛伦兹力大小计算公式和向心力公式有:evB=,解得电子圆周运动的轨道半径为:r==m=4.55×10-2m=4.55cm,恰好有:r=d=L/2,由于电子源S,可向纸面内任意方向发射电子,因此电子的运动轨迹将是过S点的一系列半径为r的等大圆,能够打到板MN上的区域范围如下图所示,实线SN表示电子刚好经过板N端时的轨迹,实线SA表示电子轨迹刚好与板相切于A点时的轨迹,因此电子打在板上可能位置的区域的长度为:l=NA,
3.
4.
5.
(1)如图所示,由几何关系可知,,解得:
粒子在磁场中做圆周运动,洛伦兹力提供向心力:,解得:
(2)粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,设轨迹半径为
洛伦兹力提供向心力:,得,其中,解得:
粒子沿与与MO成70°方向进入磁场,设粒子从区域边界P射出,其运动轨迹如图所示:
由图中几何关系可知粒子轨迹所对应的圆心角为α=160°
粒子运动周期:
则粒子在磁场中的运动的时间:
(3)粒子沿各个方向以进入磁场做匀速圆周时的轨迹半径都为,且不变,如图所示
由图可知,粒子在磁场中通过的面积等于以为圆心的扇形的面积、以M为圆心的扇形的面积和以O点为圆心的圆弧MQ与直线MQ围成的面积之和。
,,
所以:
自助作业
1.物理学家通过艰苦的实验来探究自然的物理规律,为人类的科学做出了巨大贡献,值得我
们敬仰,下列描述中符合物理学史实的是( )
A.开普勒发现了行星运动三定律,从而提出了日心学说
B.牛顿发现了万有引力定律但并未测定出引力常量G
C.奥斯特发现了电流的磁效应并提出了分子电流假说
D.法拉第发现了电磁感应现象并总结出了判断感应电流方向的规律
2.在如图所示电路中,电源电动势为E,内阻为r,电流表A、二极管和电压表V1、V2均为理
想电表,R1为定值电阻,R2为滑动变阻器。闭合开关S,当R2的滑动触头P向下滑动的过程中
( )
A.电压表V1的示数增大,电压表V2的示数减小
B.电压表V1示数的变化量的绝对值与电压表V2示数的变化量的绝对值相等
C.电容器上的电压与电流表A示数的比值不变
D.电压表V1示数的变化量与电流表A示数的变化量的比值保持不变
3.如图所示,一劲度系数为k的轻质弹簧,上端固定,下端连一质量为m的物块A,A放在质量也为m的托盘B上,以FN表示B对A的作用力,x表示弹簧的伸长量.初始时,在竖直向上的力F作用下系统静止,且弹簧处于自然状态(x=0).现改变力F的大小,使B以的加速度匀加速向下运动(g为重力加速度,空气阻力不计),此过程中FN或F随x变化的图象正确的是 ( )
4. 图中的变压器为理想变压器,原线圈匝数与副线圈匝数之比为10 ∶1,变压器的原线圈接如图所示的正弦式交流电,电阻和电容器连接成如图所示的电路,其中,电容器的击穿电压为8V,电压表V为理想交流电表,开关S处于断开状态,则下列说法正确的是( )
A.电压表V的读数约为5.07V
B.电流表A的读数为0.05A
C.电阻R2上消耗的功率为2.5W
D.若闭合开关S,电容器会被击穿
5.如图所示,一点电荷固定在光滑水平面上的O点,虚线a、b、c、d是点电荷激发电场的四条等距离的等势线。一个带电小滑块从等势线d上的1处以水平初速度v0运动,结果形成了实线所示的小滑块运动轨迹。1、2、3、4、5是等势线与小滑块运动轨迹的一些交点,由此可以判定错误的是( )
A.固定电荷与小滑块电性一定相同
B.在1、2、3、4、5五个位置上小滑块具有的动能与电势能之和一定相等
C.在整个过程中小滑块的加速度先变大后变小
D.小滑块从位置1到2和从位置3到4的过程中,电场力做功的大小关系是W12=3W34
6.如图所示,置于竖直面内的光滑金属圆环半径为r,质量为m的带孔小球穿于环上,同时有一长为r的细绳一端系于圆环最高点,当圆环以角速度绕竖直直径转动时, ( )
A.细绳对小球的拉力可能为零
B.细绳和金属圆环对小球的作用力大小可能相等
C.细绳对小球拉力与小球的重力大小不可能相等
D.当时,金属圆环对小球的作用力为零
7.如图所示,一个半径为R的导电圆环与一个轴向对称的发散磁场处处正交,环上各点的磁感应强度B大小相等,方向均与环面轴线方向成θ角(环面轴线为竖直方向)。若导线环上载有如图所示的恒定电流I,则下列说法正确的是( )
A. 导电圆环有收缩的趋势
B. 导电圆环所受安培力方向竖直向上
C. 导电圆环所受安培力的大小为2BIR
D. 导电圆环所受安培力的大小为3πBIRsinθ
8.如图所示,一轻绳吊着粗细均匀的棒,棒下端离地面高H,上端套着一个细环.棒和环的质量均为m,相互间最大静摩擦力等于滑动摩擦力,大小为kmg(k>1).断开轻绳,棒和环自由下落.假设棒足够长,与地面发生碰撞时,触地时间极短,无动能损失.棒在整个运动过程中始终保持竖直,空气阻力不计.则 ( )
A.从断开轻绳到棒和环都静止的过程中,环相对于棒有往复运动,但总位移向下
B.棒第一次与地面碰撞弹起上升过程中,棒和环都做匀减速运动
C.从断开轻绳到棒和环都静止的过程中,环相对于地面始终向下运动
D.从断开轻绳到棒和环都静止,摩擦力做的总功为-
9.(6分)将两根自然长度相同、劲度系数不同、粗细也不同的弹簧套在一起,看做一根新弹簧,设原粗弹簧(记为A)劲度系数为k1,原细弹簧(记为B)劲度系数为k2,套成的新弹簧(记为C)劲度系数为k3.关于k1、k2、k3的大小关系,同学们做出了如下猜想:
甲同学:和电阻并联相似,可能是=+
乙同学:和电阻串联相似,可能是k3=k1+k2
丙同学:可能是k3=
(1)为了验证猜想,同学们设计了相应的实验.(装置见图甲)
(2)简要实验步骤如下,请完成相应填空.
①将弹簧A悬挂在铁架台上,用刻度尺测量弹簧A的自然长度L0;
②在弹簧A的下端挂上钩码,记下钩码的个数n、每个钩码的质量m和当地的重力加速度大小g,并用刻度尺测量弹簧的长度L1;
③由F=____计算弹簧的弹力,由x=L1-L0计算弹簧的伸长量,由k=计算弹簧的劲度系数;
④改变____,重复实验步骤②、③,并求出弹簧A的劲度系数的平均值k1;
⑤仅将弹簧分别换为B、C,重复上述操作步骤,求出弹簧B、C的劲度系数的平均值k2、k3.比较k1、k2、k3并得出结论.
(3)图乙是实验得到的图线,由此可以判断____同学的猜想正确.
10.(10分)电压表改装前需要测量其内阻,测量电压表内阻的电路如图甲,所用电源为内阻可以忽略的干电池,定值电阻R1=8 000 Ω,R2=4 000 Ω.
(1)闭合S1,断开S2,调节电阻箱R,记下多组R的大小及其对应的电压表示数U;
(2)闭合S1,____,同样调节电阻箱R,记下多组R的大小及其对应的电压表示数U;将以上两次测得的多组数据,分别在坐标纸上描点连线,得到如图乙中所示两条图线;
(3)利用图线数据得出电源电动势E=____,求出电压表内阻Rv=____.两图线的交点的横坐标设为R0,还可用物理量符号R0、R1、R2表示Rv= .判断断开S2时,所得数据描绘的是图线____.(选填“AB”或“CD”)
自助作业参考答案:
1-8: B D D C D CD AB BCD
9.(6分)③nmg ④钩码的个数 (3)乙
10.(10分)(2)闭合S2 (3)3.0 V 5000 Ω AB
同课章节目录
