等腰梯形(山东省烟台市海阳市)
图片预览





文档简介
课件21张PPT。 人的逻辑推理能力,主要来自语言和数学.学好数学就等于掌握了提高逻辑推理能力的一把金钥匙.等腰梯形的判定义务教育课程标准实验教科书学习目标: 1、掌握等腰梯形的三种判定方法,能够运用等腰梯形判定方法进行有关的证明和计算。
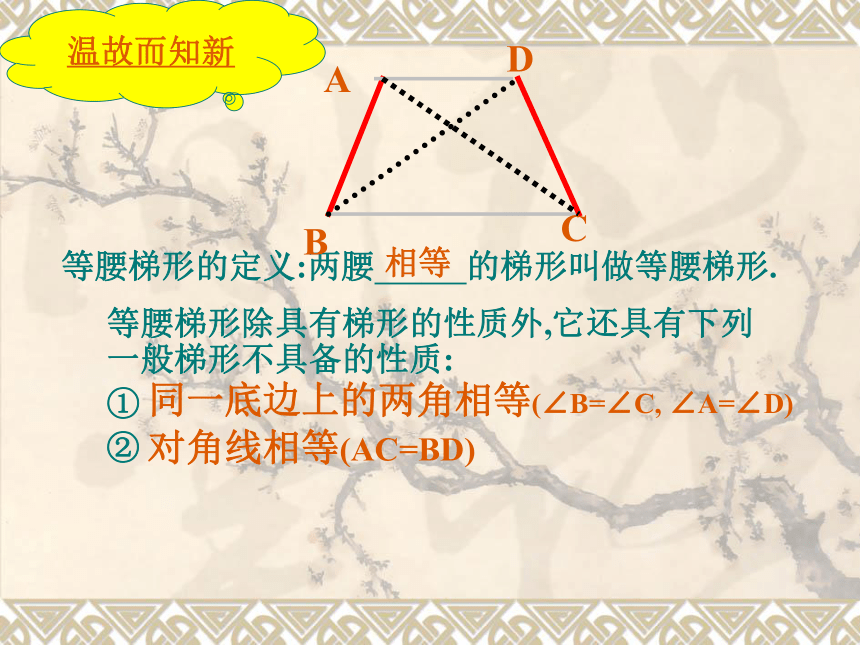
2、通过添加辅助线,把梯形问题转化成平行四边形或三角形问题,体会图形变换的方法和转化思想。 等腰梯形的定义:两腰 的梯形叫做等腰梯形.等腰梯形除具有梯形的性质外,它还具有下列一般梯形不具备的性质:
①
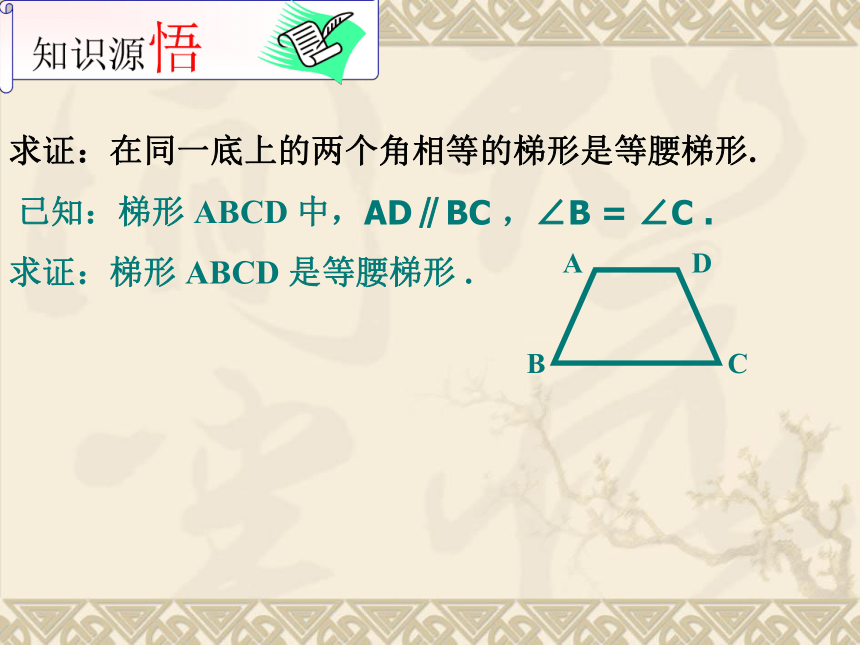
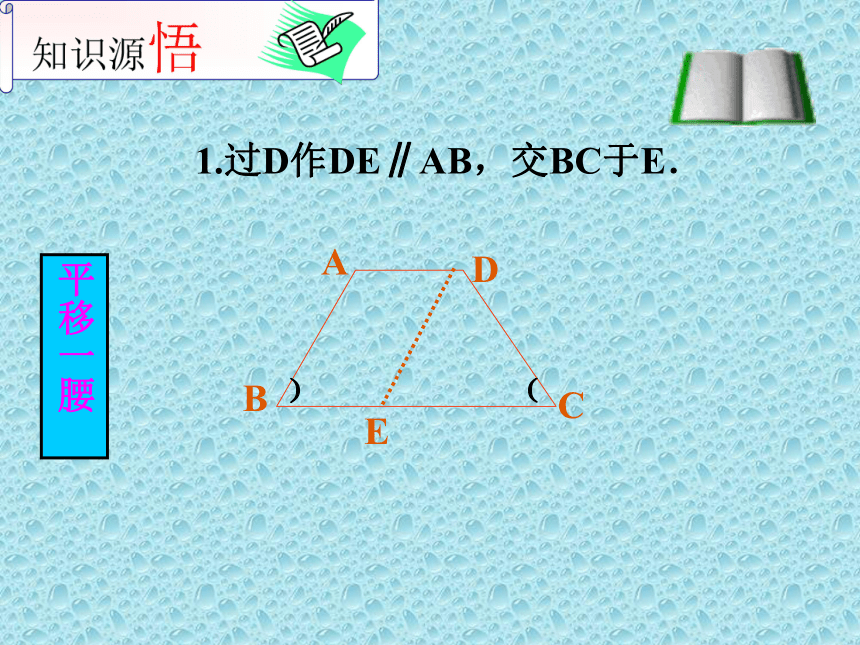
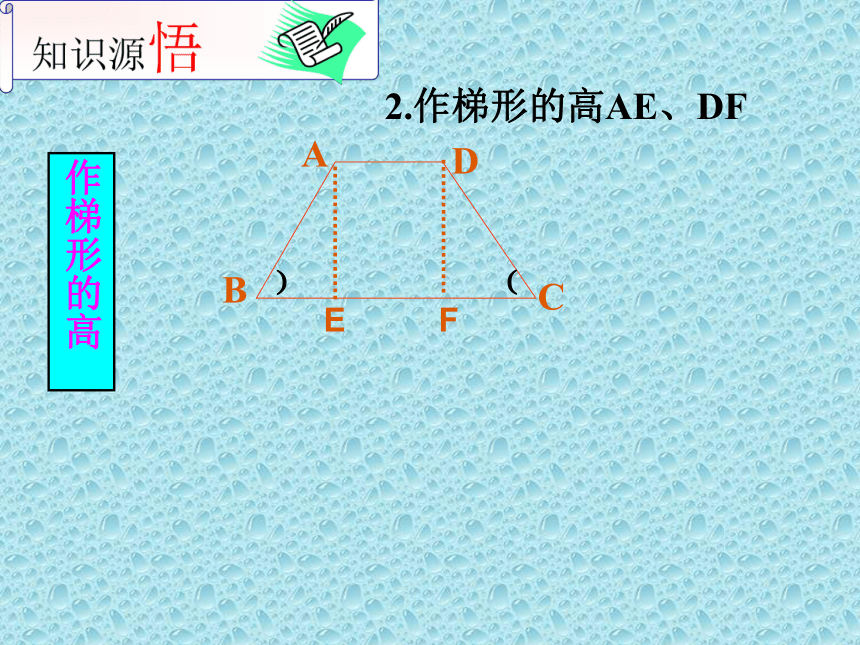
②相等同一底边上的两角相等(∠B=∠C, ∠A=∠D)对角线相等(AC=BD)BADC温故而知新思考:试说出等腰梯形性质定理的逆命题在同一底上的两个角相等的梯形是等腰梯形1.等腰梯形在同一底上的两个角相等.2.等腰梯形的对角线相等.两条对角线相等的梯形是等腰梯形逆命题:逆命题:求证:在同一底上的两个角相等的梯形是等腰梯形. 已知:梯形 ABCD 中,求证:梯形 ABCD 是等腰梯形 .AD∥BC ,∠B = ∠C .E1.过D作DE∥AB,交BC于E.平移一腰﹚﹙2.作梯形的高AE、DFEF作梯形的高﹚ ﹙3.分别延长BA、CD,它们相交于点EE可以证明△EAD和△EBC是等腰三角形从而得到AB=DC
延长两腰等腰梯形判定之二:在同一底上的两个角相等的梯形是等腰梯形已知:在梯形ABCD中,AD∥BC,AC=BD.E(2)两条对角线相等的梯形是等腰梯形求证:梯形ABCD是等腰梯形.∴ ΔABC≌ΔDCB
∴ AB=DC
∴梯形ABCD是等腰梯形
(两腰相等的梯形是等腰梯形)证明:过D作DE//AC交BC延长线于E,∵AD//BC, DE//AC
∴四边形ACED是平行四边形
∴ AC=DE∵AC=BD
∴BD=DE
∴ ∠1=∠3∵ AC//DE
∴ ∠2=∠3
∴ ∠1=∠2在ΔABC和ΔDCB中,AC=DB
∠2=∠1
BC=CB等腰梯形判定方法之三:两条对角线相等的梯形是等腰梯形. 平移对角线2.如图,梯形ABCD,AD∥BC,BE=CE,
EF⊥AB于F,EG⊥DC于G,且EF=EG.
求证:梯形ABCD是等腰梯形.‖﹨‖﹨3.如图,梯形ABCD中,AD∥BC, ∠1=∠2
求证:梯形ABCD是等腰梯形. 小结:本节课你学会了哪些知识和技巧技能?梯形梯形证明一个四边形是等腰梯形,
分两步证明:
第一步:证明四边形是 ;
第二步:证明 是等腰梯形.
梯形中常用的辅助线:E 当堂检测学无止境
没有最好,只有更好不经风雨,怎能识彩虹.未过磨历,且会就成功!1、抢答题 判断正误:(1)有两个角相等的梯形一定是等腰梯形( )(2)如果一个梯形是轴对称图形,则它一定是等腰梯形. ( )(3) 一组对边平行,另一组对边相等的四边形一定是等腰梯形. ( )√××二、选择题
1.四边形ABCD中,若∠A︰∠B︰∠C︰∠D=2︰2︰1︰1,那么这个四边形是( ).
A.梯形 B.等腰梯形
C.直角梯形 D.任意四边形
2.一等腰梯形上底为9cm,下底为17cm,一底角为60°,则它的腰长为( ).
A.8cm B.9cm
C. 7cm D.8.5cm
3.下列命题中,真命题有 ( )
①有两个角相等的梯形是等腰梯形; ②有两条边相等的梯形是等腰梯形; ③两条对角线相等的梯形是等腰梯形; ④等腰梯形上、下底中点连线,把梯形分成面积相等的两部分.
(A)1个 (B)2个 (C)3个 (D)4个BAB三: 如图,在梯形ABCD中,AD∥BC,∠A、∠C互补, 梯形ABCD是等腰梯形吗?为什么?BCAD谢谢指导
2、通过添加辅助线,把梯形问题转化成平行四边形或三角形问题,体会图形变换的方法和转化思想。 等腰梯形的定义:两腰 的梯形叫做等腰梯形.等腰梯形除具有梯形的性质外,它还具有下列一般梯形不具备的性质:
①
②相等同一底边上的两角相等(∠B=∠C, ∠A=∠D)对角线相等(AC=BD)BADC温故而知新思考:试说出等腰梯形性质定理的逆命题在同一底上的两个角相等的梯形是等腰梯形1.等腰梯形在同一底上的两个角相等.2.等腰梯形的对角线相等.两条对角线相等的梯形是等腰梯形逆命题:逆命题:求证:在同一底上的两个角相等的梯形是等腰梯形. 已知:梯形 ABCD 中,求证:梯形 ABCD 是等腰梯形 .AD∥BC ,∠B = ∠C .E1.过D作DE∥AB,交BC于E.平移一腰﹚﹙2.作梯形的高AE、DFEF作梯形的高﹚ ﹙3.分别延长BA、CD,它们相交于点EE可以证明△EAD和△EBC是等腰三角形从而得到AB=DC
延长两腰等腰梯形判定之二:在同一底上的两个角相等的梯形是等腰梯形已知:在梯形ABCD中,AD∥BC,AC=BD.E(2)两条对角线相等的梯形是等腰梯形求证:梯形ABCD是等腰梯形.∴ ΔABC≌ΔDCB
∴ AB=DC
∴梯形ABCD是等腰梯形
(两腰相等的梯形是等腰梯形)证明:过D作DE//AC交BC延长线于E,∵AD//BC, DE//AC
∴四边形ACED是平行四边形
∴ AC=DE∵AC=BD
∴BD=DE
∴ ∠1=∠3∵ AC//DE
∴ ∠2=∠3
∴ ∠1=∠2在ΔABC和ΔDCB中,AC=DB
∠2=∠1
BC=CB等腰梯形判定方法之三:两条对角线相等的梯形是等腰梯形. 平移对角线2.如图,梯形ABCD,AD∥BC,BE=CE,
EF⊥AB于F,EG⊥DC于G,且EF=EG.
求证:梯形ABCD是等腰梯形.‖﹨‖﹨3.如图,梯形ABCD中,AD∥BC, ∠1=∠2
求证:梯形ABCD是等腰梯形. 小结:本节课你学会了哪些知识和技巧技能?梯形梯形证明一个四边形是等腰梯形,
分两步证明:
第一步:证明四边形是 ;
第二步:证明 是等腰梯形.
梯形中常用的辅助线:E 当堂检测学无止境
没有最好,只有更好不经风雨,怎能识彩虹.未过磨历,且会就成功!1、抢答题 判断正误:(1)有两个角相等的梯形一定是等腰梯形( )(2)如果一个梯形是轴对称图形,则它一定是等腰梯形. ( )(3) 一组对边平行,另一组对边相等的四边形一定是等腰梯形. ( )√××二、选择题
1.四边形ABCD中,若∠A︰∠B︰∠C︰∠D=2︰2︰1︰1,那么这个四边形是( ).
A.梯形 B.等腰梯形
C.直角梯形 D.任意四边形
2.一等腰梯形上底为9cm,下底为17cm,一底角为60°,则它的腰长为( ).
A.8cm B.9cm
C. 7cm D.8.5cm
3.下列命题中,真命题有 ( )
①有两个角相等的梯形是等腰梯形; ②有两条边相等的梯形是等腰梯形; ③两条对角线相等的梯形是等腰梯形; ④等腰梯形上、下底中点连线,把梯形分成面积相等的两部分.
(A)1个 (B)2个 (C)3个 (D)4个BAB三: 如图,在梯形ABCD中,AD∥BC,∠A、∠C互补, 梯形ABCD是等腰梯形吗?为什么?BCAD谢谢指导
