五年级下册数学苏教版3.5 质数和合数课件(共15张PPT)
文档属性
| 名称 | 五年级下册数学苏教版3.5 质数和合数课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 478.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-13 15:33:27 | ||
图片预览





文档简介
(共15张PPT)
3.5 质数和合数
1.6×0.3= 473-298=
6.4-4= 0.5÷0.125=
3.6 ÷6= 5×0.24=
70×0.32= 4.86÷4÷0.25=
0.52-0.22= 3.5×0.8-3.5×0.7=
0.48
175
2.4
0.5×8=4
0.6
1.2
22.4
4.86÷1=4.86
0.21
3.5×0.1=0.35
2的因数: ;3的因数: ;
5的因数: ;6的因数: ;
8的因数: ;9的因数: ;
写出下面各数的所有因数。
在这些数中,只有两个因数的有( ),有两个以上因数的有( )。
1、2 1、3 1、5 1、2、3、6
1、2、4、8 1、3、9
2、3、5
6、8、9
例6
只有两个因数的数,它们的因数有什么特点?
2、3、5 这几个数只有 1 和它本身两个因数, 像这样的数叫作质数(或素数)。
6、8、9 这几个数除了 1 和它本身还有别的因数, 像这样的数叫作合数。
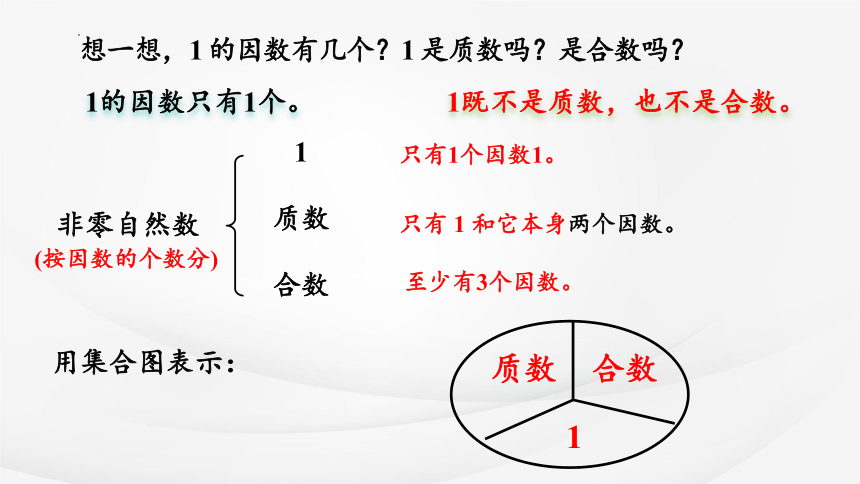
想一想,1 的因数有几个?1 是质数吗?是合数吗?
1的因数只有1个。
1既不是质数,也不是合数。
非零自然数
1
质数
合数
(按因数的个数分)
只有1个因数1。
只有 1 和它本身两个因数。
至少有3个因数。
质数 合数
1
用集合图表示:
试一试
找出 4、7 和 10 的所有因数,再写出它们分别是质数还是合数。
4 的因数有__________,4 是( )数;
7 的因数有 __________,7 是( )数;
10 的因数有___________,10 是( )数;
1 , 2 , 4
1 , 7
1 , 2 , 5 , 10
合
质
合
归纳:判断一个数是质数还是合数,只需要看这个数除了 1 和它本身两个因数外,是否还有其他因数。如果没有,这个数就是质数;如果有,这个数就是合数。
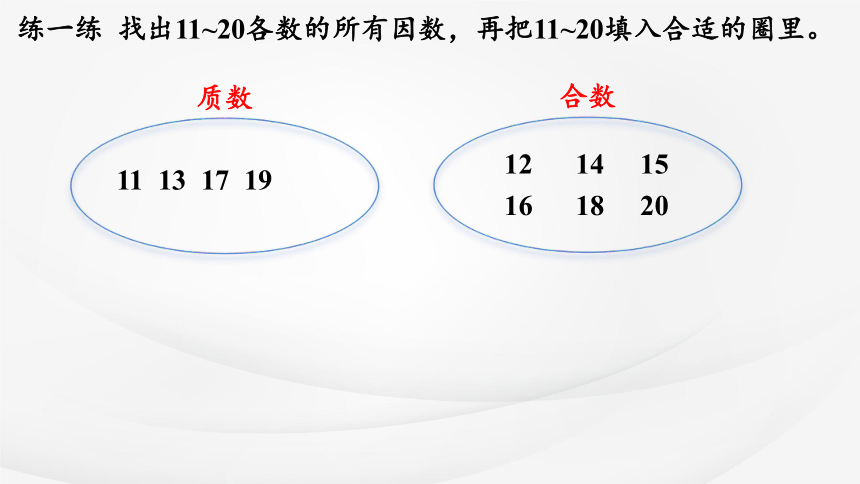
练一练 找出11~20各数的所有因数,再把11~20填入合适的圈里。
质数
合数
11 13 17 19
12 14 15
16 18 20
P38 练习六
1.从2~50中先划掉2的倍数,再依次划掉3、5、7的倍数。
(2、3、5、7本身不划掉。)
剩下的都是质数。
剩下的都是什么数?
50以内的质数有:2、3、5、7、11、13、17、19、
23、29、31、37、41、43、47。
2. 下面各数, 哪些是质数, 哪些是合数? 分别填入合适的圈里。
21 23 25 27 29 31 33 35 37 43 47 49
质数
合数
23 29 31
37 43 47
21 25 27
33 35 49
3. 找出下面每组数中的质数。
(1)13,23,33,43。
(2)5,15,25,35。
(3)17,27,37,47。
(4)19,29,39,49。
注意:判断一个数是否是质数,关键看这个数因数的个数,而不是看这个数个位上的数字。
同步练习
4.判断下列说法对不对。
(1)一个自然数,不是质数就是合数。
(2)质数加上1后都是合数。
(3)两个质数的积一定是合数。
(×)
(×)
(√)
(4)2是最小的质数,4是最小的合数。
(√)
1
2+1=3
这两个质数都是这个合数的因数
5.你会在括号里填上合适的质数吗
8=( )+( )
10=( )+( )
12=( )+( )
14=( )+( )
30=( )+( )=( )+( )
3
5
3
7
5
7
3
11
11
19
13
17
非0自然数
(按因数的个数)
质数(只有1和它本身这两个因数)
1(既不是质数,也不是合数)
合数(除了1和它本身,还有别的因数)
2、3、5、7、11、13、17、19
4、6、8、9、10、12、14、15、16、18、20
*2. 1742年,哥德巴赫提出了一个猜想:任意大于2的偶数都可以写成两个质数之和,如8=5+3。从这个猜想又可推出:任意大于5的奇数都可写成三个质数之和,如1=3+3+5,19=5+7+7。请你写出三个符合猜想的算式。
( )=( )+( )+( )
( )=( )+( )+( )
( )=( )+( )+( )
2、3、5、7、11、13、17、19
*3.一个长方形的长和宽都是质数,并且周长是80厘米。这个长方形的面积最大是多少平方厘米?
80÷2=40(厘米)
40=3+37=11+29=17+23
3×37=111(平方厘米)
11×29=319(平方厘米)
17×23=391(平方厘米)
391>319>111
答:这个长方形的面积最大是391平方厘米。
3.5 质数和合数
1.6×0.3= 473-298=
6.4-4= 0.5÷0.125=
3.6 ÷6= 5×0.24=
70×0.32= 4.86÷4÷0.25=
0.52-0.22= 3.5×0.8-3.5×0.7=
0.48
175
2.4
0.5×8=4
0.6
1.2
22.4
4.86÷1=4.86
0.21
3.5×0.1=0.35
2的因数: ;3的因数: ;
5的因数: ;6的因数: ;
8的因数: ;9的因数: ;
写出下面各数的所有因数。
在这些数中,只有两个因数的有( ),有两个以上因数的有( )。
1、2 1、3 1、5 1、2、3、6
1、2、4、8 1、3、9
2、3、5
6、8、9
例6
只有两个因数的数,它们的因数有什么特点?
2、3、5 这几个数只有 1 和它本身两个因数, 像这样的数叫作质数(或素数)。
6、8、9 这几个数除了 1 和它本身还有别的因数, 像这样的数叫作合数。
想一想,1 的因数有几个?1 是质数吗?是合数吗?
1的因数只有1个。
1既不是质数,也不是合数。
非零自然数
1
质数
合数
(按因数的个数分)
只有1个因数1。
只有 1 和它本身两个因数。
至少有3个因数。
质数 合数
1
用集合图表示:
试一试
找出 4、7 和 10 的所有因数,再写出它们分别是质数还是合数。
4 的因数有__________,4 是( )数;
7 的因数有 __________,7 是( )数;
10 的因数有___________,10 是( )数;
1 , 2 , 4
1 , 7
1 , 2 , 5 , 10
合
质
合
归纳:判断一个数是质数还是合数,只需要看这个数除了 1 和它本身两个因数外,是否还有其他因数。如果没有,这个数就是质数;如果有,这个数就是合数。
练一练 找出11~20各数的所有因数,再把11~20填入合适的圈里。
质数
合数
11 13 17 19
12 14 15
16 18 20
P38 练习六
1.从2~50中先划掉2的倍数,再依次划掉3、5、7的倍数。
(2、3、5、7本身不划掉。)
剩下的都是质数。
剩下的都是什么数?
50以内的质数有:2、3、5、7、11、13、17、19、
23、29、31、37、41、43、47。
2. 下面各数, 哪些是质数, 哪些是合数? 分别填入合适的圈里。
21 23 25 27 29 31 33 35 37 43 47 49
质数
合数
23 29 31
37 43 47
21 25 27
33 35 49
3. 找出下面每组数中的质数。
(1)13,23,33,43。
(2)5,15,25,35。
(3)17,27,37,47。
(4)19,29,39,49。
注意:判断一个数是否是质数,关键看这个数因数的个数,而不是看这个数个位上的数字。
同步练习
4.判断下列说法对不对。
(1)一个自然数,不是质数就是合数。
(2)质数加上1后都是合数。
(3)两个质数的积一定是合数。
(×)
(×)
(√)
(4)2是最小的质数,4是最小的合数。
(√)
1
2+1=3
这两个质数都是这个合数的因数
5.你会在括号里填上合适的质数吗
8=( )+( )
10=( )+( )
12=( )+( )
14=( )+( )
30=( )+( )=( )+( )
3
5
3
7
5
7
3
11
11
19
13
17
非0自然数
(按因数的个数)
质数(只有1和它本身这两个因数)
1(既不是质数,也不是合数)
合数(除了1和它本身,还有别的因数)
2、3、5、7、11、13、17、19
4、6、8、9、10、12、14、15、16、18、20
*2. 1742年,哥德巴赫提出了一个猜想:任意大于2的偶数都可以写成两个质数之和,如8=5+3。从这个猜想又可推出:任意大于5的奇数都可写成三个质数之和,如1=3+3+5,19=5+7+7。请你写出三个符合猜想的算式。
( )=( )+( )+( )
( )=( )+( )+( )
( )=( )+( )+( )
2、3、5、7、11、13、17、19
*3.一个长方形的长和宽都是质数,并且周长是80厘米。这个长方形的面积最大是多少平方厘米?
80÷2=40(厘米)
40=3+37=11+29=17+23
3×37=111(平方厘米)
11×29=319(平方厘米)
17×23=391(平方厘米)
391>319>111
答:这个长方形的面积最大是391平方厘米。
