人教版四年级下册数学第五单元三角形填空题专题训练(含解析)
文档属性
| 名称 | 人教版四年级下册数学第五单元三角形填空题专题训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 610.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 10:25:41 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
人教版四年级下册数学第五单元三角形填空题专题训练
1.如果一个三角形的两条边分别是6cm和12cm,那么它的第三条边最长是( )cm,最短是( )cm。(长度取整厘米数)
2.一个等边三角形,周长是15cm,每条边的长度是( )cm,它的每个内角是( )°。
3.一个三角形,一条边长9cm,另一条边长5cm,那么第三条边最长是( ),最短是( )。(边长取整厘米数)
4.下图中,一扇窗户打开后,可以用窗户挡风撑杆AB将其固定,窗户就不会被风吹得晃动。这里运用到的数学知识是( )。
5.一个三角形中一条边长是3cm,另一条边长是5cm,若第三条边是整厘米数,则第三条边最大是( )cm,最小是( )cm。
6.过多边形一个顶点的所有对角线将这个多边形分成4个三角形,这个多边形是( )边形,内角和是( )度。
7.等腰三角形的两个内角之比是2∶5,这个等腰三角形的底角最大可能是( )°。
8.下图中有( )个锐角,它们的和是( )°,有( )个直角,有( )个钝角。
9.一根铁丝围成的平行四边形的邻边分别是12厘米和6厘米,这个平行四边形的周长是( )厘米;用这根铁丝围成等边三角形的话,边长是( )厘米。
10.从长度分别为4cm、5cm、6cm、11cm的四根小棒中选出三根小棒围成一个三角形,这个三角形的周长是( )cm。
11.如图,已知∠1=30°,∠2=70°,那么∠3=( )°,∠4=( )°。
12.两根小棒分别长4厘米和8厘米,要想围成一个三角形,第三根小棒最长是( )厘米,最短是( )厘米(取整厘米数)。
13.一个等腰三角形的两个内角分别是40°、70°,则第三个内角是( )°,按角分这个三角形是( )三角形。
14.在一个三角形中,∠1=58°,∠2=42°,∠3=( )°;在一个直角三角形中,一个锐角是25°,另一个锐角是( )°。
15.一个等腰三角形的顶角是120°,它的底角是( )度,是( )三角形。
16.一个等腰三角形的顶角是40°,一个底角是( )°,它还是一个( )三角形;如果它的一个底角是40°,它就是一个( )三角形。(按角分类)
17.如下图,已知∠1=30°,则∠2=( )°;沿着虚线剪下这个三角形的直角,剩下部分的内角和是( )°。
18.用一根长20厘米的铁丝围成一个三角形,这个三角形的三条边可能分别长5厘米、( )厘米和( )厘米。(接头处忽略不计)
19.三角形的三边均为整数,其中两条边分别是7cm、11cm,第三条边长最长是( )cm,最短是( )cm。
20.一个等腰三角形的顶角度数是一个底角的2倍,那么它的顶角是( )°,一个底角是( )°;按角来分,它是( )三角形。
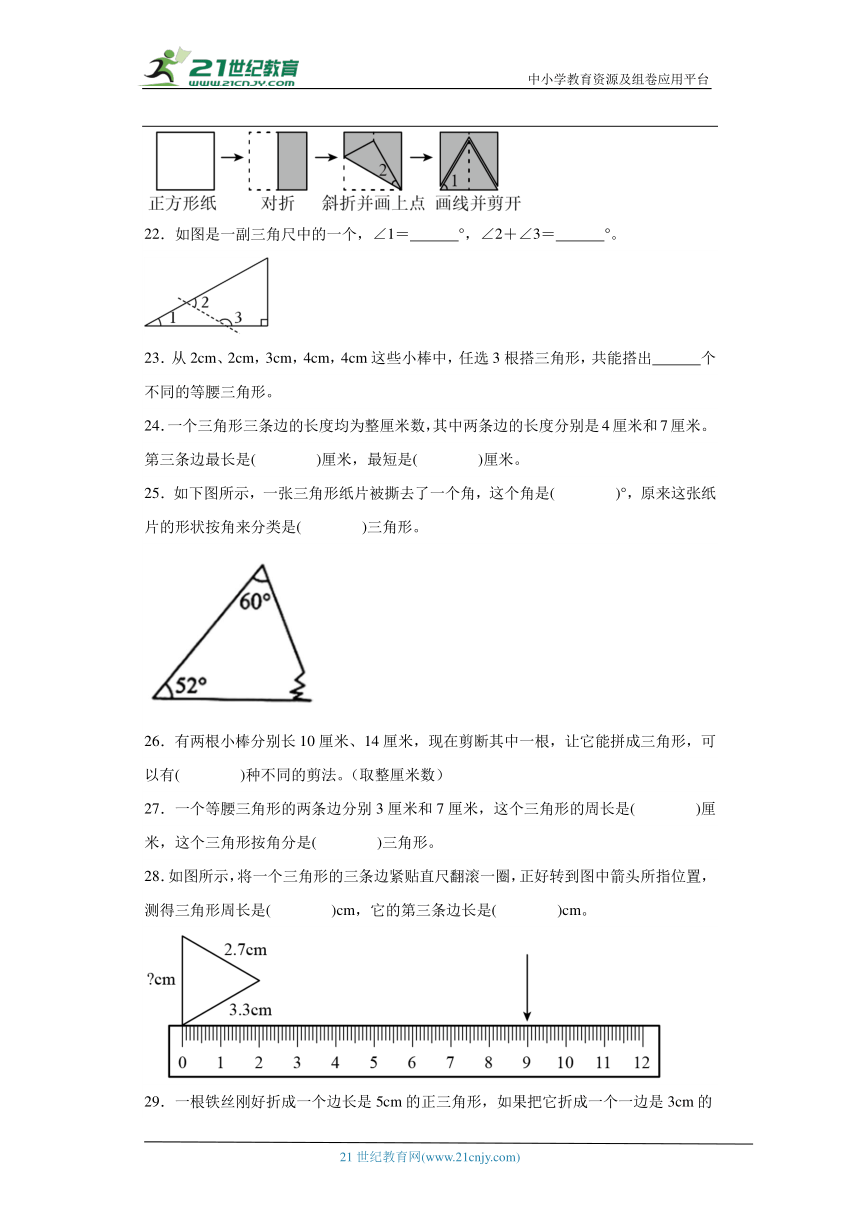
21.如下图把正方形剪成一个特殊的三角形。图中∠1=( ),∠2=( )。
22.如图是一副三角尺中的一个,∠1= °,∠2+∠3= °。
23.从2cm、2cm,3cm,4cm,4cm这些小棒中,任选3根搭三角形,共能搭出 个不同的等腰三角形。
24.一个三角形三条边的长度均为整厘米数,其中两条边的长度分别是4厘米和7厘米。第三条边最长是( )厘米,最短是( )厘米。
25.如下图所示,一张三角形纸片被撕去了一个角,这个角是( )°,原来这张纸片的形状按角来分类是( )三角形。
26.有两根小棒分别长10厘米、14厘米,现在剪断其中一根,让它能拼成三角形,可以有( )种不同的剪法。(取整厘米数)
27.一个等腰三角形的两条边分别3厘米和7厘米,这个三角形的周长是( )厘米,这个三角形按角分是( )三角形。
28.如图所示,将一个三角形的三条边紧贴直尺翻滚一圈,正好转到图中箭头所指位置,测得三角形周长是( )cm,它的第三条边长是( )cm。
29.一根铁丝刚好折成一个边长是5cm的正三角形,如果把它折成一个一边是3cm的等腰三角形,那么另两条边分别是( )cm和( )cm。
30.在一个直角三角形中,一个锐角是56°,另一个锐角是( )°。等腰三角形的一个底角是25°,它的顶角是( )°,如果按角分,它是( )三角形。
31.一个三角形指示牌既是钝角三角形,又是等腰三角形,它的一个内角是40°,其余两个内角分别是( )°和( )°。
32.一个三角形的两个内角分别是42°和84°,另一个角是( )°,它是一个( )三角形。
33.一个等腰三角形的其中两条边分别长5厘米、11厘米,那么这个等腰三角形的周长是( )厘米。
34.如图中( )个直角三角形;有( )个钝角三角形。
35.一个三角形的两个内角分别是30°和80°,另一个内角是( )°,它是一个( )三角形。
36.如图中的两个三角形都是等腰三角形,其中∠1=20°;∠2=30°。则:∠3=( );∠4=( )。
37.一个等腰三角形其中两条边分别是5厘米、11厘米,另一条边是( )厘米。这个三角形的一个底角是76°,按角分它属于( )三角形。
38.已知三角形的两个角分别是60°和60°,那么另外一个角是( )°,这个三角形按角分是( )三角形,按边分是( )三角形。
39.数一数,图中共有( )个三角形。
40.一个三角形三条边的长度都是整厘米数,其中两条边分别是5厘米和7厘米,那么第三条边最长是( )厘米,最短是( )厘米。
41.如图所示,已知△ABC中∠A=30°,那么△ABC按边分是( )三角形;沿虚线剪下一个小三角形,剩下部分图形的内角和是( )°。
42.如下图,小红说:“∠1+∠2=∠4”。小红说得对吗?( )(填“对”或“不对”),理由是( )。
43.一个等腰三角形的周长是42cm,其中一条边长9cm,和它不相等的另一条边长是( )cm。
44.等腰三角形的一个底角是45°,它的顶角是( )°,按角分类,它是( )三角形。三角形按角分类可以分成( )、( )、( )。
45.一个等腰三角形顶角的度数是一个底角度数的2倍,这个三角形的顶角是( )°,按角分类,这是一个( )三角形。
46.在一个直角三角形中,锐角∠A比锐角∠B大,∠A=( ),∠B=( )。
47.王叔叔把一根18分米长的铁丝正好折成了一个正三角形铁框,铁框一边长( )分米,若折成一条腰是5分米的等腰三角形铁框,铁框底边长( )分米。
48.六边形的内角和是( )度,把它分成若干个三角形,每个三角形的内角和都是( )度。
49.三角形的三条边都是整分米数,其中两条边的长分别是3分米和5分米,第三条边最长是( )分米,最短是( )分米。
50.三角形按角分可以分为( )三角形、( )三角形和( )三角形。三角形中最大的角至少不小于( )°。
51.一个三角形的三个内角互不相等,其中最小的内角大于45°,这个三角形按角分类属于( )三角形。
52.一个三角形每条边的长都是整厘米数。如果它的两条边长分别是4厘米和3厘米,那么这个三角形的第三条边可能是( )厘米,也可能是( )厘米。
53.在一个三角形中,∠1、∠2、∠3是它的三个内角,已知∠1=25°、∠2=140°,则∠3=( ),这是一个( )三角形。
54.在等腰三角形ABC中,顶角∠A=100°,则∠B=( )°;一个三角形的三条边的长度都是6cm,它的一个内角是( )°。
55.“红领巾心向党,争做新时代好少年。”少先队员佩戴的红领巾,按角分属于( )三角形,按边分属于( )三角形。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1. 17 7
【分析】根据三角形三边的关系“两边之和大于第三边,两边之差小于第三边”进行解答即可。
【详解】12-6<第三边<12+6
6<第三边<18
因为边的长度为整厘米数,
所以第三条边最长是17cm,最短是7cm。
2. 5 60
【分析】等边三角形的三条边相等,3个内角相等,都是60°,三角形的周长是三角形三条边的长度之和,用周长除以3即可求出其边长。
【详解】15÷3=5(cm)
一个等边三角形,周长是15cm,每条边的长度是5cm,它的每个内角是60°。
3. 13cm 5cm
【分析】在一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边;据此解答即可。
【详解】9-5=4(cm)
9+5=14(cm)
一个三角形,一条边长9cm,另一条边长5cm,那么第三条边最长是13cm,最短是5cm。
4.三角形具有稳定性
【分析】根据图片可知,挡风撑杆AB与窗户形成了一个三角形,三角形具有稳定性,据此解答即可。
【详解】挡风撑杆AB与窗户形成了一个三角形,三角形具有稳定性,所以窗户就不会被风吹得晃动。所以这里运用到的数学知识是:三角形具有稳定性。
5. 7 3
【分析】根据三角形三边关系:任意两边之和大于第三边,任意两边之差小于第三边;进行解答即可。
【详解】因为5-3<第三边<5+3,
所以2<第三边<8,
即第三边的取值在2~8cm(不包括2cm和8cm),
因为第三条边是整厘米数,所以第三条边最大是8-1=7(cm),最小是2+1=3(cm)。
6. 六 720
【分析】先画一个三角形,以三角形的一个顶点为三角形的顶点,画出4个三角形,如图可知,这是一个六边形,因为三角形的内角和是180°,而六边形能被分为4个三角形,所以六边形的内角和是4个180°,计算出180°与4的积即可求出其内角和。
【详解】
180°×4=720°
过多边形一个顶点的所有对角线将这个多边形分成四个三角形,这个多边形是六边形,内角和是720度。
7.75
【分析】等腰三角形的两个底角相等,所以当2份的角做底角时,三角形的内角和被分成了2+2+5=9份,当5份的角做底角时,三角形的内角和被分成了2+5+5=12份,据此作答即可。
【详解】2+2+5=9
180÷9×2
=20×2
=40(度)
2+5+5=12
180÷12×5
=15×5
=75(度)
40<75
这个等腰三角形的底角最大可能是75°。
【点睛】此题主要考查了等腰三角形的性质及三角形内角和是180度,注意:在没有说明谁大谁小的情况下应分为两种情况。
8. 4 180 3 1
【分析】小于90°的角是锐角,等于90°的角是直角,大于90°小于180°的角是钝角,等于180°的角是平角,三角形的内角和是180°,依此解答。
【详解】180°-90°=90°
90°×2=180°
图中,∠1、∠2、∠3、∠4都是锐角,与∠2组成平角的角是钝角,与直角组成平角的角是直角,因此填空如下:
图中有4个锐角,它们的和是180°,有3个直角,有1个钝角。
【点睛】解答此题的关键是要熟练掌握锐角、直角、钝角、平角的特点,以及应熟记三角形的内角和度数。
9. 36 12
【分析】根据平行四边形的特征,对边平行且相等,平行四边形的周长为相邻两边长度和的2倍,据此解答即可。用这根铁丝围成一个等边三角形,则等边三角形的周长等于这根铁丝的长度,也就等于平行四边形的周长。等边三角形的边长=周长÷3,据此解答即可。
【详解】(12+6)×2
=18×2
=36(厘米)
36÷3=12(厘米)
即这个平行四边形的周长是36厘米;用这根铁丝围成等边三角形的话,边长是12厘米。
【点睛】本题考查平行四边形和等边三角形的周长,熟记平行四边形和等边三角形的特征是解题关键。
10.15
【分析】根据题意得:四根小棒选出三根的情况有:4cm、5cm、6cm;4cm、5cm、11cm;5cm、6cm、11cm;4cm、6cm、11cm共4种情况,根据三角形的三边关系,任意两边之和大于第三边,选择4cm、5cm、6cm,将三边相加即可得到周长。
【详解】根据题意以及三角形三边关系,选择4cm、5cm、6cm,周长为:
4+5+6=9+6=15(cm)
【点睛】本题考查的是三角形三边关系,只要用最小的两边和相加看是否大于第三边来进行选择。
11. 110 80
【分析】根据图示可知,∠2+∠3=180°,即∠3=180°-∠2;三角形的内角和是180°,因此用180°减三角形中另外两个角的度数之和,即可计算出∠4的度数,依此解答。
【详解】180°-70°=110°
180°-(30°+70°)
=180°-100°
=80°
∠3=110°,∠4=80°。
【点睛】解答此题的关键是要熟练掌握角的分类与换算,平角的特点,以及应熟记三角形的内角和度数。
12. 11 5
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此解答即可。
【详解】4+8=12(厘米)
8-4=4(厘米)
第三根小棒的长度小于12厘米,大于4厘米,最长是11厘米,最短是5厘米(取整厘米数)。
【点睛】本题考查三角形的三边关系,关键是运用三角形的三边关系求出第三根小棒长度的取值范围。
13. 70 锐角
【分析】因为三角形的内角和为180°,已两个内角分别为40°和70°,用180°减去其中两个内角即可得到第三个内角。三角形三个内角都小于90°就是锐角三角形,三个内角有一个为90°就是直角三角形,三个内角有一个钝角就是钝角三角形。
【详解】第三个内角为:180°-40°-70°=140°-70°=70°。
三个内角都是锐角所以是锐角三角形。
【点睛】本题考查的是三角形的内角和以及按角的分类,掌握三角形内角和是180°是解答本题的关键。
14. 80 65
【分析】(1)在一个三角形中,已知两个角的度数,依据三角形的内角和是180°,即可求出另外一个角的度数;
(2)根据在直角三角形中,两个锐角的和是90°解答即可。
【详解】∠3=180°-(58°+42°)
=180°-100°
=80°
90°-25°=65°
在一个三角形中,∠1=58°,∠2=42°,∠3=80°;在一个直角三角形中,一个锐角是25°,另一个锐角是65°。
【点睛】解答此题的主要依据是:三角形的内角和定理以及直角三角形的特点。
15. 30 钝角
【分析】等腰三角形的两个底角相等,三角形的内角和等于180°,180°减顶角的度数等于两个底角的度数和,再除以2即等于一个底角的度数;顶角是钝角,这个三角形是钝角三角形。
【详解】(180°-120°)÷2
=60°÷2
=30°
一个等腰三角形的顶角是120°,它的底角是30度,是钝角三角形。
【点睛】熟练掌握三角形的分类和三角形的内角和知识是解答本题的关键。
16. 70 锐角 钝角
【分析】根据三角形的内角和是180°,等腰三角形的两个底角相等,先用180°减去顶角的度数,求出两个底角的度数和,然后除以2进行解答即可;
根据三角形内角和定理和等腰三角形的性质,用180°减去2个底角的度数,可以求得其顶角的度数;
根据三角形按角分类:有一个角大于90°小于180°的三角形是钝角三角形,有一个角是直角的三角形是直角三角形,三个角都是锐角的三角形是锐角三角形;进行判断即可。
【详解】(180°-40°)÷2
=140°÷2
=70°
180°-40°×2
=180°-80°
=100°
一个等腰三角形的顶角是40°,一个底角是70°,它还是一个锐角三角形;如果它的一个底角是40°,它就是一个钝角三角形。
【点睛】此题根据三角形内角和等于180°和等腰三角形的特点进行解答;用到的知识点:三角形的分类。
17. 60 360
【分析】三角形的内角和是180度,从图中可知三角形ABC为直角三角形,所以∠2=90°-∠1,沿着虚线剪下这个三角形的直角,剩下部分是一个四边形,四边形内角和是360度,据此解答。
【详解】∠2=90°-∠1
=90°-30°
=60°
沿着虚线剪下这个三角形的直角,剩下部分的内角和是360度。
【点睛】本题考查三角形和四边形的内角和,应熟练掌握并灵活运用。
18. 9 6
【分析】根据三角形的三边关系:两边之和大于第三边,三角形的两边的差一定小于第三边,即可解题。
【详解】由分析可知:
20-5=15(厘米)
所以这个三角形的三条边可能分别是5厘米、9厘米、6厘米,可能是5厘米、8厘米、7厘米。
【点睛】熟练掌握三角形的三边关系是解答本题的关键。
19. 17 5
【分析】根据三角形的特征:任意两边之和大于第三边,任意两边之差小于第三边;由此解答即可。
【详解】11-7<第三边<11+7,所以4<第三边<18;
因为三角形的三边均为整数,所以第三条边最长是17cm,最短是5cm。
【点睛】本题考查了三角形的特性,熟练掌握三角形三边之间的关系是解答本题的关键。
20. 90 45 直角
【分析】等腰三角形的特征:两腰相等,两底角也相等;再根据三角形内角和是180°,这个等腰三角形的顶角度数是一个底角的2倍,所以先180°÷4求得底角的度数,进而乘2求顶角的度数。然后根据角的度数区分是什么三角形,据此解答。
【详解】底角:180°÷4=45°
顶角:45°×2=90°
有一个角是90°,这个三角形是直角三角形。
【点睛】此题根据等腰三角形的特征和三角形的内角以及直角三角形的知识,掌握三角形的内角和是180°是解题的关键。
21. 60°/60度 30°/30度
【分析】斜折上去的那条边就是正方形下面那条边,因为是对折,所以得到的三角形三边相等,三角形的内角和是180°,等边三角形的三个角都相等,因此∠1=180°÷3,而2个∠2=∠1,所以∠2是∠1度数的一半;据此解答。
【详解】180°÷3=60°
60°÷2=30°
图中∠1=60°,∠2=30°。
【点睛】此题考查的是等边三角形的特点,以及三角形的内角和,应熟练掌握图形折叠的特点。
22. 30 210
【分析】一副三角尺中有两个三角形,每个三角形的三个内角分别是45°、45°、90°,30°、60°、90°。则∠1=30°,这个三角形的另一个锐角是60°。根据四边形的内角和为360°可知,∠2+∠3+60°+90°=360°,则∠2+∠3=360°-90°-60°。
【详解】360°-90°-60°=210°
则∠1=30°,∠2+∠3=210°。
【点睛】本题考查三角尺的认识以及四边形的内角和,关键是明确这个三角尺中两个锐角的度数。
23.3
【分析】等腰三角形的两条腰相等,两条腰是2cm和2cm时,第三条边是3cm或者4cm。两条腰是4cm和4cm时,第三条边是2cm或者3cm。再根据三角形的三边关系,判断各种组合中的三根小棒能否围成一个三角形。
【详解】2+2>3,则长2cm、2cm、3cm的三根小棒能围成一个等腰三角形;
2+2=4,则长2cm、2cm、4cm的三根小棒不能围成一个等腰三角形;
2+4>4,则长4cm、4cm、2cm的三根小棒能围成一个等腰三角形;
3+4>4,则长4cm、4cm、3cm的三根小棒能围成一个等腰三角形;
共能搭出3个不同的等腰三角形。
【点睛】本题考查等腰三角形的特征和三角形的三边关系,解题时先找出所有可能的组合,再根据三角形的三边关系进行判断。
24. 10 4
【分析】三角形任意两边的长度之和大于第三边,任意两边的长度之差小于第三边,依此填空即可。
【详解】4厘米+7厘米=11厘米;7厘米-4厘米=3厘米
由此可知,3厘米<第三边的长度<11厘米
3+1=4(厘米);11-1=10(厘米)
第三条边最长是10厘米,最短是4厘米。
【点睛】熟练掌握三角形三边的关系,是解答本题的关键。
25. 68 锐角
【分析】三角形的内角和是180°,因此用180°减另外两个角的度数之和即可,依此计算,最后根据三角形按角分类的标准填空即可。
【详解】180°-(60°+52°)
=180°-112°
=68°
90°>68°>60°>52°
由此可知,这个角是68°,原来这张纸片的形状按角来分类是锐角三角形。
【点睛】解答此题的关键是应熟练掌握三角形的分类标准,以及应熟记三角形的内角和度数。
26.5
【分析】根据三角形的三边关系可知,若剪断长10厘米的小棒,则三角形的最长边的长度是14厘米,其余两条边的长度和为10厘米,两边之和小于第三边,不能剪断长10厘米的小棒,应剪断长14厘米的小棒,可分成13厘米和1厘米、12厘米和2厘米、11厘米和3厘米、10厘米和4厘米、9厘米和5厘米、8厘米和6厘米、7厘米和7厘米。根据三角形的三边关系进行判断解答。
【详解】10<14,不能剪断长10厘米的小棒。
1+10<13,长13厘米、1厘米、10厘米的三根小棒不能围成一个三角形。
2+10=12,长12厘米、2厘米、10厘米的三根小棒不能围成一个三角形。
3+10>11,长11厘米、3厘米、10厘米的三根小棒能围成一个三角形。
4+10>10,长10厘米、4厘米、10厘米的三根小棒能围成一个三角形。
5+9>10,长9厘米、5厘米、10厘米的三根小棒能围成一个三角形。
6+8>10,长8厘米、6厘米、10厘米的三根小棒能围成一个三角形。
7+7>10,长7厘米、7厘米、10厘米的三根小棒能围成一个三角形。
可以有5种不同的剪法。
【点睛】本题考查三角形的三边关系,需熟练掌握,关键是明确需要剪断长14厘米的小棒。
27. 17 锐角
【分析】等腰三角形两腰相等;三角形三边之间的关系:三角形两边之和大于第三边,三角形两边之差小于第三边,据此推断出另一条边的长度;三角形的周长等于三边之和;三角形按角分可分为锐角三角形、钝角三角形和直角三角形;据此解答。
【详解】根据分析:3+3<7,3+7>7,所以这个等腰三角形的另一条边长度为7厘米,7+7+3=17(厘米),所以这个三角形的周长是17厘米;三角形两腰长度大于底的长度,所以这个三角形按角分是锐角三角形。
【点睛】本题考查的是对等腰三角形的认识,三角形周长的计算,以及三角形三边的关系,三角形的分类。
28. 9 3
【分析】根据题图可知,将这个三角形从直尺的0cm刻度线开始,紧贴直尺翻滚一圈转到的位置就是这个三角形三条边的长度和,也就是这个三角形的周长。用三角形的周长减去已知两条边的长度,求出第三条边的长度。
【详解】9-2.7-3.3=3(cm)
测得三角形周长是9cm,它的第三条边长是3cm。
【点睛】本题考查三角形周长的认识,三角形的周长等于三条边的长度和。
29. 6 6
【分析】先用正三角形的边长乘3计算出铁丝的长度,等腰三角形两腰相等,三角形任意两边之和大于第三边,据此计算出等腰三角形的另外两条边;据此解答。
【详解】根据分析:铁丝长度:5×3=15(cm);
假如3cm为底边,
(15-3)÷2
=12÷2
=6(cm)
另外两条边分别是6cm和6cm,3+6>6,可以围成三角形;
假如3cm为腰,
15-3×2
=15-6
=9(cm)
另外两条边分别是3cm和9cm,3+3<9,不能围成一个三角形;所以另两条边分别是6cm和6cm。
【点睛】本题主要考查的是三角形三边的关系。
30. 34 130 钝角
【分析】三角形的内角和等于180°,直角三角形中有一个角是90°,一个锐角是56°,则另一个锐角等于180°减90°,再减56°;等腰三角形的两个底角相等,一个底角是25°,所以顶角等于180°减2个25°,再根据顶角的度数判断是什么三角形;据此即可解答。
【详解】180°-90°-56°
=90°-56°
=34°
180°-25°-25°
=155°-25°
=130°
130°是钝角,所以这个等腰三角形是钝角三角形。
在一个直角三角形中,一个锐角是56°,另一个锐角是34°。等腰三角形的一个底角是25°,它的顶角是130°,如果按角分,它是钝角三角形。
【点睛】熟练掌握三角形内角和、等腰三角形的特征和三角形分类知识是解答本题的关键。
31. 40 100
【分析】钝角三角形有一个角是钝角;等腰三角形的两个底角相等,三角形的内角和是180°,由此可知,40°是底角,因此用180°减去2个40°即可。
【详解】它的一个内角是40°,即底角是40°;
180°-40°×2
=180°-80°
=100°
其余两个内角分别是40°和100°。
【点睛】解答此题的关键是要熟练掌握钝角三角形、等腰三角形的特点,以及应熟记三角形的内角和度数。
32. 54 锐角
【分析】根据三角形的内角和为180°可知,另一个角是180°-42°-84°=54°。这个三角形的三个角都是锐角,这个三角形就是锐角三角形。
【详解】180°-42°-84°=54°
另一个角是54°,它是一个锐角三角形。
【点睛】本题考查三角形的内角和定理和三角形的分类,关键是求出另一个角的度数。
33.27
【分析】在三角形中,两边之和大于第三边,如果腰长是5厘米,5+5=10<11,所以这个等腰三角形的腰只能为11厘米,那么把三角形的三条边相加即可得到这个等腰三角形的周长,据此解答即可。
【详解】11+11+5
=22+5
=27(厘米)
这个等腰三角形的周长是27厘米。
【点睛】此题主要考查在三角形中,两边之和大于第三边和三角形周长的计算方法。
34. 3 3
【分析】根据直角三角形是有一个角是直角的三角形,钝角三角形是有一个角是钝角的三角形,即可解题。
【详解】由分析可知:
如图中3个直角三角形;有3个钝角三角形。
【点睛】本题主要考查了直角三角形和钝角三角形的概念,需熟练掌握。
35. 70 锐角
【分析】三角形的内角和是180°,因此用180°减另外两个角的度数之和即可,依此计算,最后根据三角形按角分类的标准填空即可。
【详解】180°-(30°+80°)
=180°-110°
=70°
30°<70°<80°<90°
另一个内角是70°,它是一个锐角三角形。
【点睛】解答此题的关键是应熟练掌握三角形的分类标准,以及熟记三角形的内角和度数。
36. 120° 80°
【分析】根据等腰三角形的两个底角相等,三角形的内角和等于180°,所以∠3=180°-2∠2,∠4=180°-2(∠1+∠2),即可解题。
【详解】由分析可知:
∠3=180°-2∠2
=180°-2×30°
=180°-60°
=120°
∠4=180°-2(∠1+∠2)
=180°-2×(20°+30°)
=180°-2×50°
=180°-100°
=80°
所以∠3=120°,∠4=80°。
【点睛】本题主要考查了等腰三角形的特征和三角形内角和等于180度的知识,需熟练掌握。
37. 11 锐角
【分析】等腰三角形中的两腰相等,三角形任意两边的长度之和大于第三边,任意两边的长度之差小于第三边,依此确定出等腰三角形的腰长即可填空。
等腰三角形的两个底角相等,三角形的内角和是180°,因此用180°减2个76°即可,依此计算,最后根据三角形按角分类的标准填空即可。
【详解】当5厘米是腰长时,
5+5=10(厘米),10厘米<11厘米,因此5厘米不能是腰长
当11厘米是腰长时
5+11=16(厘米),16厘米>11厘米,11-5=6(厘米),6厘米<11厘米,因此11厘米是腰长。
180°-76°-76°=104°-76°=28°
由此可知,另一条边是11厘米。这个三角形的一个底角是76°,按角分它属于锐角三角形。
【点睛】解答此题的关键是应熟练掌握等腰三角形的特点,三角形三条边之间的关系,以及熟记三角形的内角和度数。
38. 60 锐角 等边
【分析】根据三角形的内角的和等于180°,三角形第三个角的度数可用180°减去两个锐角之和;根据等边三角形的特征:三条边都相等,三个角都是60°;因为三个角都是锐角,所以是锐角三角形;据此解答。
【详解】第三个角的度数:
180°-(60°+60°)
=180°-120°
=60°
已知三角形的两个角分别是60°和60°,那么另外一个角是60°,这个三角形按角分是锐角三角形,按边分是等边三角形。
【点睛】此题主要考查的是三角形的内角和等于180°以及三角形的分类,要熟练掌握。
39.16
【分析】观察图形可知,先数单个三角形的个数有6个,再数2个图形合成的三角形,共有3个,再数3个图形合成的三角形,共有6个,最后再加上最大的三角形共1个,据此解答即可。
【详解】6+3+6+1
=9+6+1
=15+1
=16(个)
则图中共有16个三角形。
【点睛】本题考查了组合图形的计数,数三角形的个数时,不能忽略了其中较大的三角形。
40. 11 3
【分析】根据三角形的特征:任意两边之和大于第三边,任意两边之差小于第三边;由此解答即可。
【详解】7-5<第三边<7+5,
所以:2<第三边<12,
即第三边的取值在2~12厘米(不包括2厘米和12厘米),
因为三条边的长度都是整厘米数,所以第三条边最长为:12-1=11(厘米),最短为:2+1=3(厘米)。
【点睛】此题解答关键是根据在三角形中,任意两边之和大于第三边的特征解决问题。
41. 等腰 360
【分析】三角形的内角和为180°,因此用180°减另外两个角的度数之和,从而计算出∠C的度数,再根据三角形按边分类的标准填空即可。
剩下的部分是一个四边形,四边形的内角和=(四边形的边数-2)×180°,依此计算。
【详解】180°-(120°+30°)
=180°-150°
=30°
30°=30°,即△ABC按边分是等腰三角形;
(4-2)×180°
=2×180°
=360°
剩下部分图形的内角和是360°。
【点睛】解答此题的关键是要熟练掌握等腰三角形的特点,多边形的内角和的计算方法,以及熟记三角形的内角和度数。
42. 对 因为∠1+∠2+∠3=180°,∠3+∠4=180°,所以∠1+∠2=∠4
【分析】三角形的内角和是180°,则∠1、∠2与∠3的和是180°,一个平角是180°,则∠3与∠4的和是180°,那么∠1与∠2的和等于∠4,据此解答。
【详解】分析可知,小红说得对,因为∠1+∠2+∠3=180°,∠3+∠4=180°,所以∠1+∠2=∠4。
【点睛】熟记三角形的内角和与平角的度数是解答题目的关键。
43.16.5//
【分析】9cm的边可能是三角形的底边也可能是三角形的腰,分两种情况,计算和9cm不等的另一边长度,注意要判断三边长能否构成三角形,据此解答。
【详解】当9cm的边是三角形的底边时,
腰:(42-9)÷2
=33÷2
=16.5(cm)
当9cm的边是三角形的腰时,
底:42-9×2
=42-18
=24(cm)
两腰之和是18cm小于第三边(24cm),此种情况构不成三角形。
因此,这个三角形中和9cm的边不相等的另一条边长是16.5cm。
【点睛】考查对等腰三角形特征的认识及三角形三边关系,解此题关键是分情况讨论9厘米的边是三角形的腰还是底边。
44. 90 直角 锐角三角形 直角三角形 钝角三角形
【分析】等腰三角形的两腰相等,两个底角相等,三角形的内角和是180°,因此用180°减2个45°即可,依此计算,最后根据三角形按角分类的标准填空即可。
【详解】45°+45°=90°
180°-90°=90°
等腰三角形的一个底角是45°,它的顶角是90°,按角分类,它是直角三角形。三角形按角分类可以分成锐角三角形、直角三角形、钝角三角形。
【点睛】解答此题的关键是应熟练掌握等腰三角形的特点,三角形的分类标准,以及熟记三角形的内角和。
45. 90 直角
【分析】等腰三角形中两个底角相等,顶角的度数是一个底角度数的2倍,则这个等腰三角形的内角和是一个底角度数的4倍,根据三角形的内角和为180°可知,一个底角的度数是180°÷4=45°,顶角就是45°×2=90°。根据有一个直角的三角形叫做直角三角形,可知这个三角形是直角三角形。
【详解】一个底角:180°÷(1+2+1)
=180°÷4
=45°
顶角:45°×2=90°
由此判断,这是一个直角三角形。
【点睛】本题考查三角形的分类和三角形的内角和定理,关键是明确一个底角度数的4倍是180°。
46. 60° 30°
【分析】三角形内角和是180°,在直角三角形中,去掉一个直角,另两个锐角的和是90°,知道两个锐角的和,也知道两个锐角的差,按和差问题的解答方法解答即可。
已知大小两个数的和与它们的差,求大、小两个数的问题解答方法:
小数=(和-差)÷2,大数=和-小数=小数+差
大数=(和+差)÷2,小数=和-大数=大数-差
【详解】∠A+∠B+直角=180°,∠A+∠B=90°;
∠A=(30°+90°)÷2
=120°÷2
=60°
∠B=60°-30°=30°
【点睛】熟悉和差问题的解答方法是解答此题的关键。
47. 6 8
【分析】等边三角形也叫正三角形,三条边相等,18分米长的铁丝是三角形的周长,利用周长除以3即可求出等边三角形的边长;等腰三角形的两条腰相等,利用周长减去两条腰长即可求出底边长。
【详解】18÷3=6(分米)
18-5×2
=18-10
=8(分米)
王叔叔把一根18分米长的铁丝正好折成了一个正三角形铁框,铁框一边长6分米,若折成一条腰是5分米的等腰三角形铁框,铁框底边长8分米。
【点睛】熟练掌握等边三角形和等腰三角形的特征,是解答此题的关键。
48. 720 180
【分析】多边形的内角和=(多边形的边数-2)×180°,六边形有6条边,三角形的内角和是180°,依此计算并填空。
【详解】(6-2)×180°
=4×180°
=720°
六边形的内角和是720度,把它分成若干个三角形,每个三角形的内角和都是180度。
【点睛】解答此题的关键是要熟练掌握多边形内角和的计算方法,以及熟记三角形的内角和度数。
49. 7 3
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此解答即可。
【详解】3+5=8(分米)
5-3=2(分米)
第三条边的长度小于8分米,大于2分米,则最长是7分米,最短是3分米。
【点睛】熟练掌握三角形的三边关系,灵活运用三角形的三边关系解决问题。
50. 锐角 直角 钝角 60
【分析】根据三角形的分类:按角的大小分为锐角三角形,直角三角形,钝角三角形;三角形的内角和是180°,如果最大内角小于60°,那么三角形的三个内角和小于180°,因此三角形的最大内角不能小于60°,但可以等于60°。
【详解】由分析可知:
三角形按角分可以分为锐角三角形、直角三角形和钝角三角形。三角形中最大的角至少不小于60°。
【点睛】本题考查三角形的分类,三角形可以按照角或者边分类,应注意区分,不要混淆。
51.锐角
【分析】三角形中最小的内角一定是锐角,最小的内角大于45°,那么其它两个内角的和一定小于135°,假设剩下的两个内角中有一个角为90°,那么有一个内角的度数小于45°,与题意不符,所以剩下的两个内角应该都大于45°且小于90°,三角形的三个内角都是锐角,所以这个三角形是锐角三角形,据此解答。
【详解】三角形的内角和为180°。
180°-45°=135°
因为最小的内角大于45°,所以其它两个内角的和小于135°。
假设其它两个内角中有一个内角是90°。
135°-90°=45°
因为最小的内角大于45°,所以其它两个内角分别大于45°且小于90°,三个角都是锐角的三角形是锐角三角形。
【点睛】本题主要考查三角形的内角和与三角形的分类情况,分析出三个内角都是锐角是解答题目的关键。
52. 2 6
【分析】紧扣三角形三边关系,任意两边之和大于第三边,任意两边之差小于第三边,由此解答即可。
【详解】由题意得:
(4-3)厘米<第三边长<(4+3)厘米,
1厘米<第三边长<7厘米,
因为第三边长是整数,所以第三边的长度最小为2厘米,最大为6厘米;
即:这个三角形的第三条边可能是2、3、4厘米,也可能是5、6厘米。(答案不唯一)
【点睛】此题主要考查了三角形三边关系的灵活应用。
53. 15° 钝角
【分析】三角形的内角和为180°,据此可知,∠3=180°-∠1-∠2。∠2是一个钝角,根据“有一个钝角的三角形叫做钝角三角形”,可知这是一个钝角三角形。
【详解】∠3=180°-∠1-∠2=180°-25°-140°=15°
这是一个钝角三角形。
【点睛】本题考查三角形内角和定理和三角形的分类, 180°与已知两个内角度数和的差就是第三个内角的度数。
54. 40 60
【分析】等腰三角形的两个底角相等,三角形的内角和为180°,因此用180°减去100°后,再除以2,即可得到其中一个底角的度数,依此计算。
三条边都相等的三角形是等边三角形,等边三角形的三个角都相等,因此用180°除以3,即可计算出它的一个内角度数,依此计算。
【详解】180°-100°=80°
80°÷2=40°
180°÷3=60°
即∠B=40°;一个三角形的三条边的长度都是6cm,它的一个内角是60°。
【点睛】解答此题的关键是要熟练掌握等边三角形、等腰三角形的特点,以及熟记三角形的内角和度数。
55. 钝角 等腰
【分析】有一个角是钝角的三角形是钝角三角形,三个角都是锐角的三角形是锐角三角形,有一个角是直角的三角形是直角三角形;两腰相等,两个底角相等的三角形是等腰三角形;三条边都相等,三个角都相等的三角形是等边三角形,依此填空。
【详解】根据三角形的分类标准可知,少先队员佩戴的红领巾,按角分属于钝角三角形,按边分属于等腰三角形。
【点睛】熟练掌握三角形的分类标准是解答此题的关键。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
人教版四年级下册数学第五单元三角形填空题专题训练
1.如果一个三角形的两条边分别是6cm和12cm,那么它的第三条边最长是( )cm,最短是( )cm。(长度取整厘米数)
2.一个等边三角形,周长是15cm,每条边的长度是( )cm,它的每个内角是( )°。
3.一个三角形,一条边长9cm,另一条边长5cm,那么第三条边最长是( ),最短是( )。(边长取整厘米数)
4.下图中,一扇窗户打开后,可以用窗户挡风撑杆AB将其固定,窗户就不会被风吹得晃动。这里运用到的数学知识是( )。
5.一个三角形中一条边长是3cm,另一条边长是5cm,若第三条边是整厘米数,则第三条边最大是( )cm,最小是( )cm。
6.过多边形一个顶点的所有对角线将这个多边形分成4个三角形,这个多边形是( )边形,内角和是( )度。
7.等腰三角形的两个内角之比是2∶5,这个等腰三角形的底角最大可能是( )°。
8.下图中有( )个锐角,它们的和是( )°,有( )个直角,有( )个钝角。
9.一根铁丝围成的平行四边形的邻边分别是12厘米和6厘米,这个平行四边形的周长是( )厘米;用这根铁丝围成等边三角形的话,边长是( )厘米。
10.从长度分别为4cm、5cm、6cm、11cm的四根小棒中选出三根小棒围成一个三角形,这个三角形的周长是( )cm。
11.如图,已知∠1=30°,∠2=70°,那么∠3=( )°,∠4=( )°。
12.两根小棒分别长4厘米和8厘米,要想围成一个三角形,第三根小棒最长是( )厘米,最短是( )厘米(取整厘米数)。
13.一个等腰三角形的两个内角分别是40°、70°,则第三个内角是( )°,按角分这个三角形是( )三角形。
14.在一个三角形中,∠1=58°,∠2=42°,∠3=( )°;在一个直角三角形中,一个锐角是25°,另一个锐角是( )°。
15.一个等腰三角形的顶角是120°,它的底角是( )度,是( )三角形。
16.一个等腰三角形的顶角是40°,一个底角是( )°,它还是一个( )三角形;如果它的一个底角是40°,它就是一个( )三角形。(按角分类)
17.如下图,已知∠1=30°,则∠2=( )°;沿着虚线剪下这个三角形的直角,剩下部分的内角和是( )°。
18.用一根长20厘米的铁丝围成一个三角形,这个三角形的三条边可能分别长5厘米、( )厘米和( )厘米。(接头处忽略不计)
19.三角形的三边均为整数,其中两条边分别是7cm、11cm,第三条边长最长是( )cm,最短是( )cm。
20.一个等腰三角形的顶角度数是一个底角的2倍,那么它的顶角是( )°,一个底角是( )°;按角来分,它是( )三角形。
21.如下图把正方形剪成一个特殊的三角形。图中∠1=( ),∠2=( )。
22.如图是一副三角尺中的一个,∠1= °,∠2+∠3= °。
23.从2cm、2cm,3cm,4cm,4cm这些小棒中,任选3根搭三角形,共能搭出 个不同的等腰三角形。
24.一个三角形三条边的长度均为整厘米数,其中两条边的长度分别是4厘米和7厘米。第三条边最长是( )厘米,最短是( )厘米。
25.如下图所示,一张三角形纸片被撕去了一个角,这个角是( )°,原来这张纸片的形状按角来分类是( )三角形。
26.有两根小棒分别长10厘米、14厘米,现在剪断其中一根,让它能拼成三角形,可以有( )种不同的剪法。(取整厘米数)
27.一个等腰三角形的两条边分别3厘米和7厘米,这个三角形的周长是( )厘米,这个三角形按角分是( )三角形。
28.如图所示,将一个三角形的三条边紧贴直尺翻滚一圈,正好转到图中箭头所指位置,测得三角形周长是( )cm,它的第三条边长是( )cm。
29.一根铁丝刚好折成一个边长是5cm的正三角形,如果把它折成一个一边是3cm的等腰三角形,那么另两条边分别是( )cm和( )cm。
30.在一个直角三角形中,一个锐角是56°,另一个锐角是( )°。等腰三角形的一个底角是25°,它的顶角是( )°,如果按角分,它是( )三角形。
31.一个三角形指示牌既是钝角三角形,又是等腰三角形,它的一个内角是40°,其余两个内角分别是( )°和( )°。
32.一个三角形的两个内角分别是42°和84°,另一个角是( )°,它是一个( )三角形。
33.一个等腰三角形的其中两条边分别长5厘米、11厘米,那么这个等腰三角形的周长是( )厘米。
34.如图中( )个直角三角形;有( )个钝角三角形。
35.一个三角形的两个内角分别是30°和80°,另一个内角是( )°,它是一个( )三角形。
36.如图中的两个三角形都是等腰三角形,其中∠1=20°;∠2=30°。则:∠3=( );∠4=( )。
37.一个等腰三角形其中两条边分别是5厘米、11厘米,另一条边是( )厘米。这个三角形的一个底角是76°,按角分它属于( )三角形。
38.已知三角形的两个角分别是60°和60°,那么另外一个角是( )°,这个三角形按角分是( )三角形,按边分是( )三角形。
39.数一数,图中共有( )个三角形。
40.一个三角形三条边的长度都是整厘米数,其中两条边分别是5厘米和7厘米,那么第三条边最长是( )厘米,最短是( )厘米。
41.如图所示,已知△ABC中∠A=30°,那么△ABC按边分是( )三角形;沿虚线剪下一个小三角形,剩下部分图形的内角和是( )°。
42.如下图,小红说:“∠1+∠2=∠4”。小红说得对吗?( )(填“对”或“不对”),理由是( )。
43.一个等腰三角形的周长是42cm,其中一条边长9cm,和它不相等的另一条边长是( )cm。
44.等腰三角形的一个底角是45°,它的顶角是( )°,按角分类,它是( )三角形。三角形按角分类可以分成( )、( )、( )。
45.一个等腰三角形顶角的度数是一个底角度数的2倍,这个三角形的顶角是( )°,按角分类,这是一个( )三角形。
46.在一个直角三角形中,锐角∠A比锐角∠B大,∠A=( ),∠B=( )。
47.王叔叔把一根18分米长的铁丝正好折成了一个正三角形铁框,铁框一边长( )分米,若折成一条腰是5分米的等腰三角形铁框,铁框底边长( )分米。
48.六边形的内角和是( )度,把它分成若干个三角形,每个三角形的内角和都是( )度。
49.三角形的三条边都是整分米数,其中两条边的长分别是3分米和5分米,第三条边最长是( )分米,最短是( )分米。
50.三角形按角分可以分为( )三角形、( )三角形和( )三角形。三角形中最大的角至少不小于( )°。
51.一个三角形的三个内角互不相等,其中最小的内角大于45°,这个三角形按角分类属于( )三角形。
52.一个三角形每条边的长都是整厘米数。如果它的两条边长分别是4厘米和3厘米,那么这个三角形的第三条边可能是( )厘米,也可能是( )厘米。
53.在一个三角形中,∠1、∠2、∠3是它的三个内角,已知∠1=25°、∠2=140°,则∠3=( ),这是一个( )三角形。
54.在等腰三角形ABC中,顶角∠A=100°,则∠B=( )°;一个三角形的三条边的长度都是6cm,它的一个内角是( )°。
55.“红领巾心向党,争做新时代好少年。”少先队员佩戴的红领巾,按角分属于( )三角形,按边分属于( )三角形。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1. 17 7
【分析】根据三角形三边的关系“两边之和大于第三边,两边之差小于第三边”进行解答即可。
【详解】12-6<第三边<12+6
6<第三边<18
因为边的长度为整厘米数,
所以第三条边最长是17cm,最短是7cm。
2. 5 60
【分析】等边三角形的三条边相等,3个内角相等,都是60°,三角形的周长是三角形三条边的长度之和,用周长除以3即可求出其边长。
【详解】15÷3=5(cm)
一个等边三角形,周长是15cm,每条边的长度是5cm,它的每个内角是60°。
3. 13cm 5cm
【分析】在一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边;据此解答即可。
【详解】9-5=4(cm)
9+5=14(cm)
一个三角形,一条边长9cm,另一条边长5cm,那么第三条边最长是13cm,最短是5cm。
4.三角形具有稳定性
【分析】根据图片可知,挡风撑杆AB与窗户形成了一个三角形,三角形具有稳定性,据此解答即可。
【详解】挡风撑杆AB与窗户形成了一个三角形,三角形具有稳定性,所以窗户就不会被风吹得晃动。所以这里运用到的数学知识是:三角形具有稳定性。
5. 7 3
【分析】根据三角形三边关系:任意两边之和大于第三边,任意两边之差小于第三边;进行解答即可。
【详解】因为5-3<第三边<5+3,
所以2<第三边<8,
即第三边的取值在2~8cm(不包括2cm和8cm),
因为第三条边是整厘米数,所以第三条边最大是8-1=7(cm),最小是2+1=3(cm)。
6. 六 720
【分析】先画一个三角形,以三角形的一个顶点为三角形的顶点,画出4个三角形,如图可知,这是一个六边形,因为三角形的内角和是180°,而六边形能被分为4个三角形,所以六边形的内角和是4个180°,计算出180°与4的积即可求出其内角和。
【详解】
180°×4=720°
过多边形一个顶点的所有对角线将这个多边形分成四个三角形,这个多边形是六边形,内角和是720度。
7.75
【分析】等腰三角形的两个底角相等,所以当2份的角做底角时,三角形的内角和被分成了2+2+5=9份,当5份的角做底角时,三角形的内角和被分成了2+5+5=12份,据此作答即可。
【详解】2+2+5=9
180÷9×2
=20×2
=40(度)
2+5+5=12
180÷12×5
=15×5
=75(度)
40<75
这个等腰三角形的底角最大可能是75°。
【点睛】此题主要考查了等腰三角形的性质及三角形内角和是180度,注意:在没有说明谁大谁小的情况下应分为两种情况。
8. 4 180 3 1
【分析】小于90°的角是锐角,等于90°的角是直角,大于90°小于180°的角是钝角,等于180°的角是平角,三角形的内角和是180°,依此解答。
【详解】180°-90°=90°
90°×2=180°
图中,∠1、∠2、∠3、∠4都是锐角,与∠2组成平角的角是钝角,与直角组成平角的角是直角,因此填空如下:
图中有4个锐角,它们的和是180°,有3个直角,有1个钝角。
【点睛】解答此题的关键是要熟练掌握锐角、直角、钝角、平角的特点,以及应熟记三角形的内角和度数。
9. 36 12
【分析】根据平行四边形的特征,对边平行且相等,平行四边形的周长为相邻两边长度和的2倍,据此解答即可。用这根铁丝围成一个等边三角形,则等边三角形的周长等于这根铁丝的长度,也就等于平行四边形的周长。等边三角形的边长=周长÷3,据此解答即可。
【详解】(12+6)×2
=18×2
=36(厘米)
36÷3=12(厘米)
即这个平行四边形的周长是36厘米;用这根铁丝围成等边三角形的话,边长是12厘米。
【点睛】本题考查平行四边形和等边三角形的周长,熟记平行四边形和等边三角形的特征是解题关键。
10.15
【分析】根据题意得:四根小棒选出三根的情况有:4cm、5cm、6cm;4cm、5cm、11cm;5cm、6cm、11cm;4cm、6cm、11cm共4种情况,根据三角形的三边关系,任意两边之和大于第三边,选择4cm、5cm、6cm,将三边相加即可得到周长。
【详解】根据题意以及三角形三边关系,选择4cm、5cm、6cm,周长为:
4+5+6=9+6=15(cm)
【点睛】本题考查的是三角形三边关系,只要用最小的两边和相加看是否大于第三边来进行选择。
11. 110 80
【分析】根据图示可知,∠2+∠3=180°,即∠3=180°-∠2;三角形的内角和是180°,因此用180°减三角形中另外两个角的度数之和,即可计算出∠4的度数,依此解答。
【详解】180°-70°=110°
180°-(30°+70°)
=180°-100°
=80°
∠3=110°,∠4=80°。
【点睛】解答此题的关键是要熟练掌握角的分类与换算,平角的特点,以及应熟记三角形的内角和度数。
12. 11 5
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此解答即可。
【详解】4+8=12(厘米)
8-4=4(厘米)
第三根小棒的长度小于12厘米,大于4厘米,最长是11厘米,最短是5厘米(取整厘米数)。
【点睛】本题考查三角形的三边关系,关键是运用三角形的三边关系求出第三根小棒长度的取值范围。
13. 70 锐角
【分析】因为三角形的内角和为180°,已两个内角分别为40°和70°,用180°减去其中两个内角即可得到第三个内角。三角形三个内角都小于90°就是锐角三角形,三个内角有一个为90°就是直角三角形,三个内角有一个钝角就是钝角三角形。
【详解】第三个内角为:180°-40°-70°=140°-70°=70°。
三个内角都是锐角所以是锐角三角形。
【点睛】本题考查的是三角形的内角和以及按角的分类,掌握三角形内角和是180°是解答本题的关键。
14. 80 65
【分析】(1)在一个三角形中,已知两个角的度数,依据三角形的内角和是180°,即可求出另外一个角的度数;
(2)根据在直角三角形中,两个锐角的和是90°解答即可。
【详解】∠3=180°-(58°+42°)
=180°-100°
=80°
90°-25°=65°
在一个三角形中,∠1=58°,∠2=42°,∠3=80°;在一个直角三角形中,一个锐角是25°,另一个锐角是65°。
【点睛】解答此题的主要依据是:三角形的内角和定理以及直角三角形的特点。
15. 30 钝角
【分析】等腰三角形的两个底角相等,三角形的内角和等于180°,180°减顶角的度数等于两个底角的度数和,再除以2即等于一个底角的度数;顶角是钝角,这个三角形是钝角三角形。
【详解】(180°-120°)÷2
=60°÷2
=30°
一个等腰三角形的顶角是120°,它的底角是30度,是钝角三角形。
【点睛】熟练掌握三角形的分类和三角形的内角和知识是解答本题的关键。
16. 70 锐角 钝角
【分析】根据三角形的内角和是180°,等腰三角形的两个底角相等,先用180°减去顶角的度数,求出两个底角的度数和,然后除以2进行解答即可;
根据三角形内角和定理和等腰三角形的性质,用180°减去2个底角的度数,可以求得其顶角的度数;
根据三角形按角分类:有一个角大于90°小于180°的三角形是钝角三角形,有一个角是直角的三角形是直角三角形,三个角都是锐角的三角形是锐角三角形;进行判断即可。
【详解】(180°-40°)÷2
=140°÷2
=70°
180°-40°×2
=180°-80°
=100°
一个等腰三角形的顶角是40°,一个底角是70°,它还是一个锐角三角形;如果它的一个底角是40°,它就是一个钝角三角形。
【点睛】此题根据三角形内角和等于180°和等腰三角形的特点进行解答;用到的知识点:三角形的分类。
17. 60 360
【分析】三角形的内角和是180度,从图中可知三角形ABC为直角三角形,所以∠2=90°-∠1,沿着虚线剪下这个三角形的直角,剩下部分是一个四边形,四边形内角和是360度,据此解答。
【详解】∠2=90°-∠1
=90°-30°
=60°
沿着虚线剪下这个三角形的直角,剩下部分的内角和是360度。
【点睛】本题考查三角形和四边形的内角和,应熟练掌握并灵活运用。
18. 9 6
【分析】根据三角形的三边关系:两边之和大于第三边,三角形的两边的差一定小于第三边,即可解题。
【详解】由分析可知:
20-5=15(厘米)
所以这个三角形的三条边可能分别是5厘米、9厘米、6厘米,可能是5厘米、8厘米、7厘米。
【点睛】熟练掌握三角形的三边关系是解答本题的关键。
19. 17 5
【分析】根据三角形的特征:任意两边之和大于第三边,任意两边之差小于第三边;由此解答即可。
【详解】11-7<第三边<11+7,所以4<第三边<18;
因为三角形的三边均为整数,所以第三条边最长是17cm,最短是5cm。
【点睛】本题考查了三角形的特性,熟练掌握三角形三边之间的关系是解答本题的关键。
20. 90 45 直角
【分析】等腰三角形的特征:两腰相等,两底角也相等;再根据三角形内角和是180°,这个等腰三角形的顶角度数是一个底角的2倍,所以先180°÷4求得底角的度数,进而乘2求顶角的度数。然后根据角的度数区分是什么三角形,据此解答。
【详解】底角:180°÷4=45°
顶角:45°×2=90°
有一个角是90°,这个三角形是直角三角形。
【点睛】此题根据等腰三角形的特征和三角形的内角以及直角三角形的知识,掌握三角形的内角和是180°是解题的关键。
21. 60°/60度 30°/30度
【分析】斜折上去的那条边就是正方形下面那条边,因为是对折,所以得到的三角形三边相等,三角形的内角和是180°,等边三角形的三个角都相等,因此∠1=180°÷3,而2个∠2=∠1,所以∠2是∠1度数的一半;据此解答。
【详解】180°÷3=60°
60°÷2=30°
图中∠1=60°,∠2=30°。
【点睛】此题考查的是等边三角形的特点,以及三角形的内角和,应熟练掌握图形折叠的特点。
22. 30 210
【分析】一副三角尺中有两个三角形,每个三角形的三个内角分别是45°、45°、90°,30°、60°、90°。则∠1=30°,这个三角形的另一个锐角是60°。根据四边形的内角和为360°可知,∠2+∠3+60°+90°=360°,则∠2+∠3=360°-90°-60°。
【详解】360°-90°-60°=210°
则∠1=30°,∠2+∠3=210°。
【点睛】本题考查三角尺的认识以及四边形的内角和,关键是明确这个三角尺中两个锐角的度数。
23.3
【分析】等腰三角形的两条腰相等,两条腰是2cm和2cm时,第三条边是3cm或者4cm。两条腰是4cm和4cm时,第三条边是2cm或者3cm。再根据三角形的三边关系,判断各种组合中的三根小棒能否围成一个三角形。
【详解】2+2>3,则长2cm、2cm、3cm的三根小棒能围成一个等腰三角形;
2+2=4,则长2cm、2cm、4cm的三根小棒不能围成一个等腰三角形;
2+4>4,则长4cm、4cm、2cm的三根小棒能围成一个等腰三角形;
3+4>4,则长4cm、4cm、3cm的三根小棒能围成一个等腰三角形;
共能搭出3个不同的等腰三角形。
【点睛】本题考查等腰三角形的特征和三角形的三边关系,解题时先找出所有可能的组合,再根据三角形的三边关系进行判断。
24. 10 4
【分析】三角形任意两边的长度之和大于第三边,任意两边的长度之差小于第三边,依此填空即可。
【详解】4厘米+7厘米=11厘米;7厘米-4厘米=3厘米
由此可知,3厘米<第三边的长度<11厘米
3+1=4(厘米);11-1=10(厘米)
第三条边最长是10厘米,最短是4厘米。
【点睛】熟练掌握三角形三边的关系,是解答本题的关键。
25. 68 锐角
【分析】三角形的内角和是180°,因此用180°减另外两个角的度数之和即可,依此计算,最后根据三角形按角分类的标准填空即可。
【详解】180°-(60°+52°)
=180°-112°
=68°
90°>68°>60°>52°
由此可知,这个角是68°,原来这张纸片的形状按角来分类是锐角三角形。
【点睛】解答此题的关键是应熟练掌握三角形的分类标准,以及应熟记三角形的内角和度数。
26.5
【分析】根据三角形的三边关系可知,若剪断长10厘米的小棒,则三角形的最长边的长度是14厘米,其余两条边的长度和为10厘米,两边之和小于第三边,不能剪断长10厘米的小棒,应剪断长14厘米的小棒,可分成13厘米和1厘米、12厘米和2厘米、11厘米和3厘米、10厘米和4厘米、9厘米和5厘米、8厘米和6厘米、7厘米和7厘米。根据三角形的三边关系进行判断解答。
【详解】10<14,不能剪断长10厘米的小棒。
1+10<13,长13厘米、1厘米、10厘米的三根小棒不能围成一个三角形。
2+10=12,长12厘米、2厘米、10厘米的三根小棒不能围成一个三角形。
3+10>11,长11厘米、3厘米、10厘米的三根小棒能围成一个三角形。
4+10>10,长10厘米、4厘米、10厘米的三根小棒能围成一个三角形。
5+9>10,长9厘米、5厘米、10厘米的三根小棒能围成一个三角形。
6+8>10,长8厘米、6厘米、10厘米的三根小棒能围成一个三角形。
7+7>10,长7厘米、7厘米、10厘米的三根小棒能围成一个三角形。
可以有5种不同的剪法。
【点睛】本题考查三角形的三边关系,需熟练掌握,关键是明确需要剪断长14厘米的小棒。
27. 17 锐角
【分析】等腰三角形两腰相等;三角形三边之间的关系:三角形两边之和大于第三边,三角形两边之差小于第三边,据此推断出另一条边的长度;三角形的周长等于三边之和;三角形按角分可分为锐角三角形、钝角三角形和直角三角形;据此解答。
【详解】根据分析:3+3<7,3+7>7,所以这个等腰三角形的另一条边长度为7厘米,7+7+3=17(厘米),所以这个三角形的周长是17厘米;三角形两腰长度大于底的长度,所以这个三角形按角分是锐角三角形。
【点睛】本题考查的是对等腰三角形的认识,三角形周长的计算,以及三角形三边的关系,三角形的分类。
28. 9 3
【分析】根据题图可知,将这个三角形从直尺的0cm刻度线开始,紧贴直尺翻滚一圈转到的位置就是这个三角形三条边的长度和,也就是这个三角形的周长。用三角形的周长减去已知两条边的长度,求出第三条边的长度。
【详解】9-2.7-3.3=3(cm)
测得三角形周长是9cm,它的第三条边长是3cm。
【点睛】本题考查三角形周长的认识,三角形的周长等于三条边的长度和。
29. 6 6
【分析】先用正三角形的边长乘3计算出铁丝的长度,等腰三角形两腰相等,三角形任意两边之和大于第三边,据此计算出等腰三角形的另外两条边;据此解答。
【详解】根据分析:铁丝长度:5×3=15(cm);
假如3cm为底边,
(15-3)÷2
=12÷2
=6(cm)
另外两条边分别是6cm和6cm,3+6>6,可以围成三角形;
假如3cm为腰,
15-3×2
=15-6
=9(cm)
另外两条边分别是3cm和9cm,3+3<9,不能围成一个三角形;所以另两条边分别是6cm和6cm。
【点睛】本题主要考查的是三角形三边的关系。
30. 34 130 钝角
【分析】三角形的内角和等于180°,直角三角形中有一个角是90°,一个锐角是56°,则另一个锐角等于180°减90°,再减56°;等腰三角形的两个底角相等,一个底角是25°,所以顶角等于180°减2个25°,再根据顶角的度数判断是什么三角形;据此即可解答。
【详解】180°-90°-56°
=90°-56°
=34°
180°-25°-25°
=155°-25°
=130°
130°是钝角,所以这个等腰三角形是钝角三角形。
在一个直角三角形中,一个锐角是56°,另一个锐角是34°。等腰三角形的一个底角是25°,它的顶角是130°,如果按角分,它是钝角三角形。
【点睛】熟练掌握三角形内角和、等腰三角形的特征和三角形分类知识是解答本题的关键。
31. 40 100
【分析】钝角三角形有一个角是钝角;等腰三角形的两个底角相等,三角形的内角和是180°,由此可知,40°是底角,因此用180°减去2个40°即可。
【详解】它的一个内角是40°,即底角是40°;
180°-40°×2
=180°-80°
=100°
其余两个内角分别是40°和100°。
【点睛】解答此题的关键是要熟练掌握钝角三角形、等腰三角形的特点,以及应熟记三角形的内角和度数。
32. 54 锐角
【分析】根据三角形的内角和为180°可知,另一个角是180°-42°-84°=54°。这个三角形的三个角都是锐角,这个三角形就是锐角三角形。
【详解】180°-42°-84°=54°
另一个角是54°,它是一个锐角三角形。
【点睛】本题考查三角形的内角和定理和三角形的分类,关键是求出另一个角的度数。
33.27
【分析】在三角形中,两边之和大于第三边,如果腰长是5厘米,5+5=10<11,所以这个等腰三角形的腰只能为11厘米,那么把三角形的三条边相加即可得到这个等腰三角形的周长,据此解答即可。
【详解】11+11+5
=22+5
=27(厘米)
这个等腰三角形的周长是27厘米。
【点睛】此题主要考查在三角形中,两边之和大于第三边和三角形周长的计算方法。
34. 3 3
【分析】根据直角三角形是有一个角是直角的三角形,钝角三角形是有一个角是钝角的三角形,即可解题。
【详解】由分析可知:
如图中3个直角三角形;有3个钝角三角形。
【点睛】本题主要考查了直角三角形和钝角三角形的概念,需熟练掌握。
35. 70 锐角
【分析】三角形的内角和是180°,因此用180°减另外两个角的度数之和即可,依此计算,最后根据三角形按角分类的标准填空即可。
【详解】180°-(30°+80°)
=180°-110°
=70°
30°<70°<80°<90°
另一个内角是70°,它是一个锐角三角形。
【点睛】解答此题的关键是应熟练掌握三角形的分类标准,以及熟记三角形的内角和度数。
36. 120° 80°
【分析】根据等腰三角形的两个底角相等,三角形的内角和等于180°,所以∠3=180°-2∠2,∠4=180°-2(∠1+∠2),即可解题。
【详解】由分析可知:
∠3=180°-2∠2
=180°-2×30°
=180°-60°
=120°
∠4=180°-2(∠1+∠2)
=180°-2×(20°+30°)
=180°-2×50°
=180°-100°
=80°
所以∠3=120°,∠4=80°。
【点睛】本题主要考查了等腰三角形的特征和三角形内角和等于180度的知识,需熟练掌握。
37. 11 锐角
【分析】等腰三角形中的两腰相等,三角形任意两边的长度之和大于第三边,任意两边的长度之差小于第三边,依此确定出等腰三角形的腰长即可填空。
等腰三角形的两个底角相等,三角形的内角和是180°,因此用180°减2个76°即可,依此计算,最后根据三角形按角分类的标准填空即可。
【详解】当5厘米是腰长时,
5+5=10(厘米),10厘米<11厘米,因此5厘米不能是腰长
当11厘米是腰长时
5+11=16(厘米),16厘米>11厘米,11-5=6(厘米),6厘米<11厘米,因此11厘米是腰长。
180°-76°-76°=104°-76°=28°
由此可知,另一条边是11厘米。这个三角形的一个底角是76°,按角分它属于锐角三角形。
【点睛】解答此题的关键是应熟练掌握等腰三角形的特点,三角形三条边之间的关系,以及熟记三角形的内角和度数。
38. 60 锐角 等边
【分析】根据三角形的内角的和等于180°,三角形第三个角的度数可用180°减去两个锐角之和;根据等边三角形的特征:三条边都相等,三个角都是60°;因为三个角都是锐角,所以是锐角三角形;据此解答。
【详解】第三个角的度数:
180°-(60°+60°)
=180°-120°
=60°
已知三角形的两个角分别是60°和60°,那么另外一个角是60°,这个三角形按角分是锐角三角形,按边分是等边三角形。
【点睛】此题主要考查的是三角形的内角和等于180°以及三角形的分类,要熟练掌握。
39.16
【分析】观察图形可知,先数单个三角形的个数有6个,再数2个图形合成的三角形,共有3个,再数3个图形合成的三角形,共有6个,最后再加上最大的三角形共1个,据此解答即可。
【详解】6+3+6+1
=9+6+1
=15+1
=16(个)
则图中共有16个三角形。
【点睛】本题考查了组合图形的计数,数三角形的个数时,不能忽略了其中较大的三角形。
40. 11 3
【分析】根据三角形的特征:任意两边之和大于第三边,任意两边之差小于第三边;由此解答即可。
【详解】7-5<第三边<7+5,
所以:2<第三边<12,
即第三边的取值在2~12厘米(不包括2厘米和12厘米),
因为三条边的长度都是整厘米数,所以第三条边最长为:12-1=11(厘米),最短为:2+1=3(厘米)。
【点睛】此题解答关键是根据在三角形中,任意两边之和大于第三边的特征解决问题。
41. 等腰 360
【分析】三角形的内角和为180°,因此用180°减另外两个角的度数之和,从而计算出∠C的度数,再根据三角形按边分类的标准填空即可。
剩下的部分是一个四边形,四边形的内角和=(四边形的边数-2)×180°,依此计算。
【详解】180°-(120°+30°)
=180°-150°
=30°
30°=30°,即△ABC按边分是等腰三角形;
(4-2)×180°
=2×180°
=360°
剩下部分图形的内角和是360°。
【点睛】解答此题的关键是要熟练掌握等腰三角形的特点,多边形的内角和的计算方法,以及熟记三角形的内角和度数。
42. 对 因为∠1+∠2+∠3=180°,∠3+∠4=180°,所以∠1+∠2=∠4
【分析】三角形的内角和是180°,则∠1、∠2与∠3的和是180°,一个平角是180°,则∠3与∠4的和是180°,那么∠1与∠2的和等于∠4,据此解答。
【详解】分析可知,小红说得对,因为∠1+∠2+∠3=180°,∠3+∠4=180°,所以∠1+∠2=∠4。
【点睛】熟记三角形的内角和与平角的度数是解答题目的关键。
43.16.5//
【分析】9cm的边可能是三角形的底边也可能是三角形的腰,分两种情况,计算和9cm不等的另一边长度,注意要判断三边长能否构成三角形,据此解答。
【详解】当9cm的边是三角形的底边时,
腰:(42-9)÷2
=33÷2
=16.5(cm)
当9cm的边是三角形的腰时,
底:42-9×2
=42-18
=24(cm)
两腰之和是18cm小于第三边(24cm),此种情况构不成三角形。
因此,这个三角形中和9cm的边不相等的另一条边长是16.5cm。
【点睛】考查对等腰三角形特征的认识及三角形三边关系,解此题关键是分情况讨论9厘米的边是三角形的腰还是底边。
44. 90 直角 锐角三角形 直角三角形 钝角三角形
【分析】等腰三角形的两腰相等,两个底角相等,三角形的内角和是180°,因此用180°减2个45°即可,依此计算,最后根据三角形按角分类的标准填空即可。
【详解】45°+45°=90°
180°-90°=90°
等腰三角形的一个底角是45°,它的顶角是90°,按角分类,它是直角三角形。三角形按角分类可以分成锐角三角形、直角三角形、钝角三角形。
【点睛】解答此题的关键是应熟练掌握等腰三角形的特点,三角形的分类标准,以及熟记三角形的内角和。
45. 90 直角
【分析】等腰三角形中两个底角相等,顶角的度数是一个底角度数的2倍,则这个等腰三角形的内角和是一个底角度数的4倍,根据三角形的内角和为180°可知,一个底角的度数是180°÷4=45°,顶角就是45°×2=90°。根据有一个直角的三角形叫做直角三角形,可知这个三角形是直角三角形。
【详解】一个底角:180°÷(1+2+1)
=180°÷4
=45°
顶角:45°×2=90°
由此判断,这是一个直角三角形。
【点睛】本题考查三角形的分类和三角形的内角和定理,关键是明确一个底角度数的4倍是180°。
46. 60° 30°
【分析】三角形内角和是180°,在直角三角形中,去掉一个直角,另两个锐角的和是90°,知道两个锐角的和,也知道两个锐角的差,按和差问题的解答方法解答即可。
已知大小两个数的和与它们的差,求大、小两个数的问题解答方法:
小数=(和-差)÷2,大数=和-小数=小数+差
大数=(和+差)÷2,小数=和-大数=大数-差
【详解】∠A+∠B+直角=180°,∠A+∠B=90°;
∠A=(30°+90°)÷2
=120°÷2
=60°
∠B=60°-30°=30°
【点睛】熟悉和差问题的解答方法是解答此题的关键。
47. 6 8
【分析】等边三角形也叫正三角形,三条边相等,18分米长的铁丝是三角形的周长,利用周长除以3即可求出等边三角形的边长;等腰三角形的两条腰相等,利用周长减去两条腰长即可求出底边长。
【详解】18÷3=6(分米)
18-5×2
=18-10
=8(分米)
王叔叔把一根18分米长的铁丝正好折成了一个正三角形铁框,铁框一边长6分米,若折成一条腰是5分米的等腰三角形铁框,铁框底边长8分米。
【点睛】熟练掌握等边三角形和等腰三角形的特征,是解答此题的关键。
48. 720 180
【分析】多边形的内角和=(多边形的边数-2)×180°,六边形有6条边,三角形的内角和是180°,依此计算并填空。
【详解】(6-2)×180°
=4×180°
=720°
六边形的内角和是720度,把它分成若干个三角形,每个三角形的内角和都是180度。
【点睛】解答此题的关键是要熟练掌握多边形内角和的计算方法,以及熟记三角形的内角和度数。
49. 7 3
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此解答即可。
【详解】3+5=8(分米)
5-3=2(分米)
第三条边的长度小于8分米,大于2分米,则最长是7分米,最短是3分米。
【点睛】熟练掌握三角形的三边关系,灵活运用三角形的三边关系解决问题。
50. 锐角 直角 钝角 60
【分析】根据三角形的分类:按角的大小分为锐角三角形,直角三角形,钝角三角形;三角形的内角和是180°,如果最大内角小于60°,那么三角形的三个内角和小于180°,因此三角形的最大内角不能小于60°,但可以等于60°。
【详解】由分析可知:
三角形按角分可以分为锐角三角形、直角三角形和钝角三角形。三角形中最大的角至少不小于60°。
【点睛】本题考查三角形的分类,三角形可以按照角或者边分类,应注意区分,不要混淆。
51.锐角
【分析】三角形中最小的内角一定是锐角,最小的内角大于45°,那么其它两个内角的和一定小于135°,假设剩下的两个内角中有一个角为90°,那么有一个内角的度数小于45°,与题意不符,所以剩下的两个内角应该都大于45°且小于90°,三角形的三个内角都是锐角,所以这个三角形是锐角三角形,据此解答。
【详解】三角形的内角和为180°。
180°-45°=135°
因为最小的内角大于45°,所以其它两个内角的和小于135°。
假设其它两个内角中有一个内角是90°。
135°-90°=45°
因为最小的内角大于45°,所以其它两个内角分别大于45°且小于90°,三个角都是锐角的三角形是锐角三角形。
【点睛】本题主要考查三角形的内角和与三角形的分类情况,分析出三个内角都是锐角是解答题目的关键。
52. 2 6
【分析】紧扣三角形三边关系,任意两边之和大于第三边,任意两边之差小于第三边,由此解答即可。
【详解】由题意得:
(4-3)厘米<第三边长<(4+3)厘米,
1厘米<第三边长<7厘米,
因为第三边长是整数,所以第三边的长度最小为2厘米,最大为6厘米;
即:这个三角形的第三条边可能是2、3、4厘米,也可能是5、6厘米。(答案不唯一)
【点睛】此题主要考查了三角形三边关系的灵活应用。
53. 15° 钝角
【分析】三角形的内角和为180°,据此可知,∠3=180°-∠1-∠2。∠2是一个钝角,根据“有一个钝角的三角形叫做钝角三角形”,可知这是一个钝角三角形。
【详解】∠3=180°-∠1-∠2=180°-25°-140°=15°
这是一个钝角三角形。
【点睛】本题考查三角形内角和定理和三角形的分类, 180°与已知两个内角度数和的差就是第三个内角的度数。
54. 40 60
【分析】等腰三角形的两个底角相等,三角形的内角和为180°,因此用180°减去100°后,再除以2,即可得到其中一个底角的度数,依此计算。
三条边都相等的三角形是等边三角形,等边三角形的三个角都相等,因此用180°除以3,即可计算出它的一个内角度数,依此计算。
【详解】180°-100°=80°
80°÷2=40°
180°÷3=60°
即∠B=40°;一个三角形的三条边的长度都是6cm,它的一个内角是60°。
【点睛】解答此题的关键是要熟练掌握等边三角形、等腰三角形的特点,以及熟记三角形的内角和度数。
55. 钝角 等腰
【分析】有一个角是钝角的三角形是钝角三角形,三个角都是锐角的三角形是锐角三角形,有一个角是直角的三角形是直角三角形;两腰相等,两个底角相等的三角形是等腰三角形;三条边都相等,三个角都相等的三角形是等边三角形,依此填空。
【详解】根据三角形的分类标准可知,少先队员佩戴的红领巾,按角分属于钝角三角形,按边分属于等腰三角形。
【点睛】熟练掌握三角形的分类标准是解答此题的关键。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
