十二、简单机械 复习课件(共43张PPT) 2023-2024学年人教版物理九年级
文档属性
| 名称 | 十二、简单机械 复习课件(共43张PPT) 2023-2024学年人教版物理九年级 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-03-13 00:00:00 | ||
图片预览







文档简介
(共43张PPT)
十二章 简单杠杆
人教版 物理
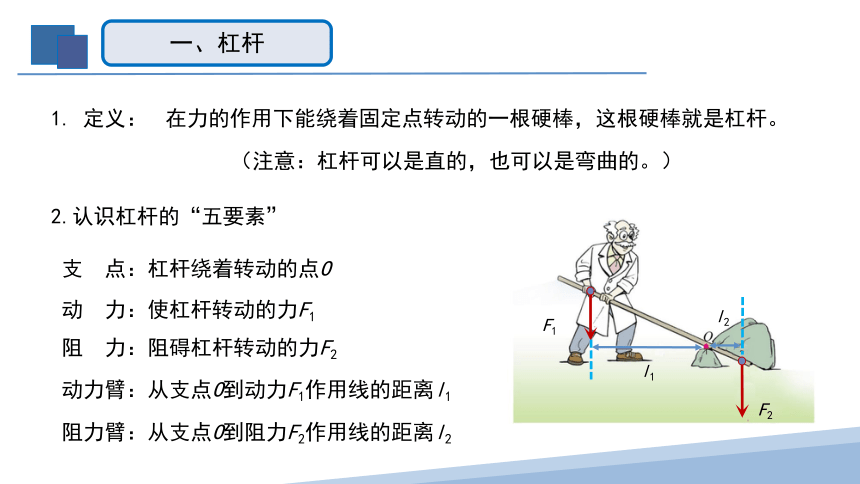
1. 定义:
在力的作用下能绕着固定点转动的一根硬棒,这根硬棒就是杠杆。
(注意:杠杆可以是直的,也可以是弯曲的。)
2.认识杠杆的“五要素”
支 点:杠杆绕着转动的点O
动 力:使杠杆转动的力F1
阻 力:阻碍杠杆转动的力F2
动力臂:从支点O到动力F1作用线的距离l1
阻力臂:从支点O到阻力F2作用线的距离l2
F1
F2
l1
l2
一、杠杆
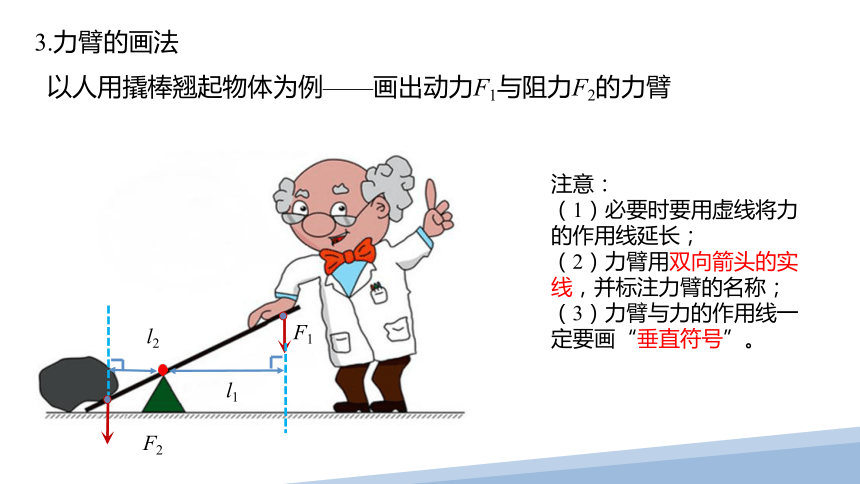
3.力臂的画法
以人用撬棒翘起物体为例——画出动力F1与阻力F2的力臂
注意:
(1)必要时要用虚线将力的作用线延长;
(2)力臂用双向箭头的实线,并标注力臂的名称;
(3)力臂与力的作用线一定要画“垂直符号”。
F1
F2
O
l1
l2
2.该实验需改变力和力臂来实现多次实验的目的:
避免偶然性,使实验结论具有普遍性。
二、杠杆的平衡条件
1.调节杠杆在水平位置平衡的目的:
3.杠杆的平衡条件是:
F1 l1 = F2 l2
(1)可以从杠杆上直接读出力臂,不用测量。
(2)可以消除杠杆自身的重力对实验结果的影响。
动力×动力臂=阻力×阻力臂
省力杠杆
等臂杠杆
省力杠杆
费力杠杆
省力杠杆
省力杠杆
“生活中的杠杆”,判断下面生活中常见的工具属于哪类杠杆?
想想议议
杠杆种类 力臂的关系 力的关系 特点 应用举例
省力杠杆 撬棒、起瓶器、手推车、夹钳等
费力杠杆 镊子、钓鱼竿、筷子、船桨等
等臂杠杆 天平、定滑轮等
L1>L2
F1<F2
省力费距离
F1>F2
费力省距离
L1=L2
F1=F2
既不省力也不省距离
L1<L2
杠杆的分类
滑轮:边缘有凹槽,能绕轴转动的小轮。
三、滑轮
1.实验探究:使用定滑轮的特点
①拉力与重力的大小关系:F=G,即使用定滑轮不省力。
②拉力的方向:可以改变。
③拉力(自由端)移动距离S绳与钩码上升高度h物的关系: 相等。
实验分析
定滑轮的特点:
不省力,不省距离,但可以改变力的方向。
定滑轮的实质:相当于一个能够连续转动的等臂杠杆。
定滑轮的实质
如图所示,定滑轮的轴心O为支点,动力臂l1与阻力臂l2都是滑轮的半径r。
由杠杆平衡的条件:F1l1=F2l2
即:Fl1=Gl2
力臂始终相等,则力相等
2.实验探究:使用动滑轮的特点。
注意:
用力缓慢拉动弹簧测力计竖直向上匀速运动。
动滑轮
①拉力与重力的关系:F<G,即使用动滑轮省力。若不计动滑轮的重力及摩擦力时,则拉力:F=G/2。
②拉力的方向:不能改变。
③拉力(绳末端)移动距离S绳与钩码上升高度h物的关系: S绳=2h物。
实验分析
使用动滑轮的特点:
能省力,但要费距离,且不能改变动力的方向。
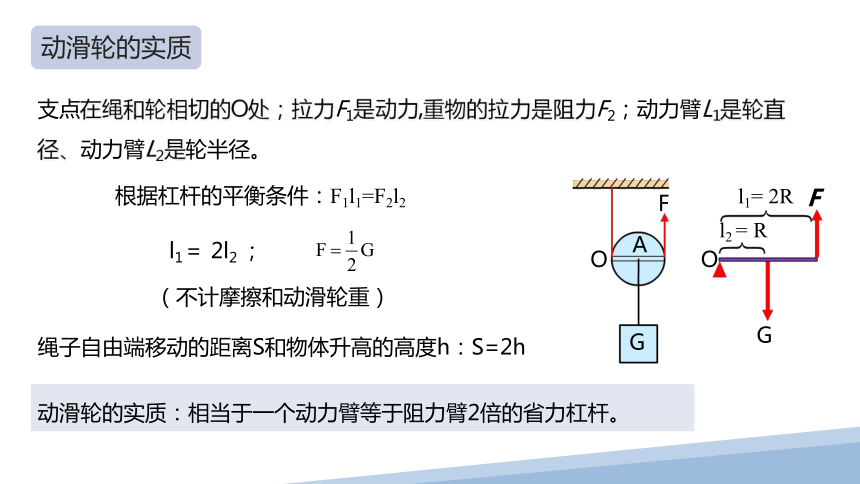
支点在绳和轮相切的O处;拉力F1是动力,重物的拉力是阻力F2;动力臂L1是轮直径、动力臂L2是轮半径。
根据杠杆的平衡条件:F1l1=F2l2
l1= 2l2 ;
绳子自由端移动的距离S和物体升高的高度h:S=2h
动滑轮的实质
动滑轮的实质:相当于一个动力臂等于阻力臂2倍的省力杠杆。
(不计摩擦和动滑轮重)
O
A
F
l2 = R
l1= 2R
O
G
F
G
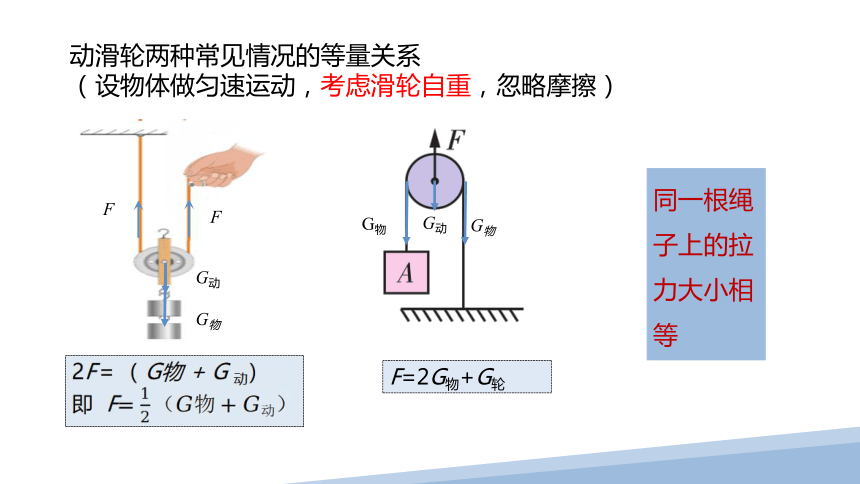
动滑轮两种常见情况的等量关系
(设物体做匀速运动,考虑滑轮自重,忽略摩擦)
F
F
2F=( G物 + G 动)
即 F
同一根绳子上的拉力大小相等
G动
G物
G动
G物
G物
F=2G物+G轮
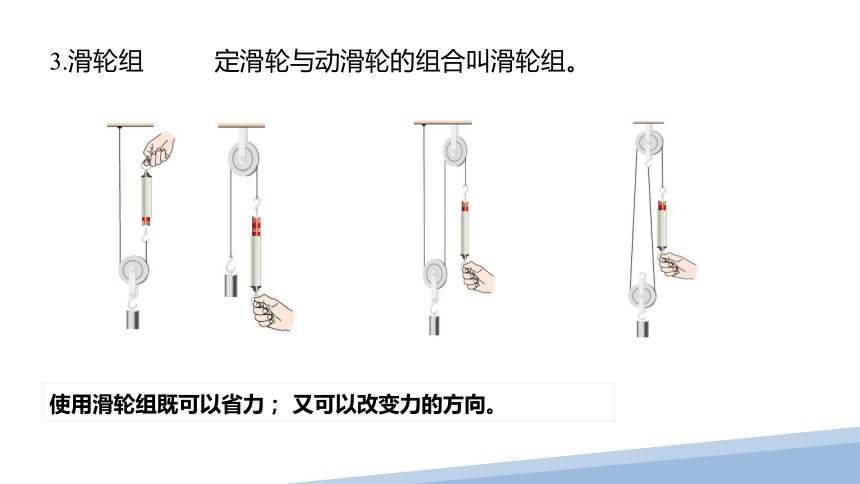
3.滑轮组
定滑轮与动滑轮的组合叫滑轮组。
使用滑轮组既可以省力; 又可以改变力的方向。
分析判断滑轮组的省力与费距离的情况
G物
F1
F2
n=3
s=3h
不计动滑轮的重和摩擦:
计动滑轮的重和摩擦:
s=3h
F2
F1
G物
n=2
s=2h
不计动滑轮的重和摩擦:
计动滑轮的重和摩擦:
s=2h
结论:使用滑轮组省了力,但是费距离。
F
F
结论:
n为承担物重的绳子段数。
讨 论
5. 机械效率总是小于1的,通常用百分数表示。
1. 意义:
机械效率是反映机械做功性能的物理量。
2. 定义:
物理学中,将有用功跟总功的比值叫做机械效率。
3. 符号:
用“η”表示。
4. 公式:
η
=
W有
W总
在保证所做有用功一定的情况下,人们总是希望额外功越少越好。即额外功在总功中所占的比例越少越好。
总功:有用功与额外功之和。 (W总= W有+ W额)
四、机械效率
6.机械效率的三种类型
类型1· 滑轮组竖直提升重物
①有用功:
W有=Gh
②总 功:
W总=Fs
③机械效率:
④额外功:
W额= G动h
(不计绳重和摩擦)
s
h
η
=
W有
W总
=
Gh
Fs
=
G
nF
类型2·滑轮组水平拉动物体(不计滑轮及绳重)
①有用功:
W有= f s物
②总 功:
W总=Fs绳
③机械效率:
s绳
s物
f
η
=
W有
W总
=
f s物
Fs绳
=
f
nF
类型3·用斜面提升物体
①有用功:
W有=Gh
②总 功:
W总=Fs
③机械效率:
η
=
W有
W总
=
Gh
Fs
④额外功:
W额= f s
s
f
7.实验探究 测量滑轮组的机械效率
实验原理:
η
=
W有
W总
=
Gh
Fs
甲 乙
注意事项:
竖直向上缓慢(匀速)拉动测力计。
结论:动滑轮重一定时,物重越大,机械效率越高。
物重一定时,动滑轮越重,机械效率越低。
提高机械效率的方法:
改进滑轮结构,减轻动滑轮自重;
在机械承受的范围内,增加物重;
减小机械间的摩擦(加润滑油)。
杠杆、滑轮作图
专项1
画杠杆力臂的一般步骤为:首先找到力的作用线(过力的作用点沿力的方向画的一条直线),然后从支点向力的作用线作垂线,垂线段的长即为力臂。
类型一 力臂作图
1.用如图所示的装置来改变照明灯的高度,轻质杠杆ABO可绕O点转动,请在图中画出拉起杠杆的动力F的力臂l1及杠杆受到的阻力F′。
2.如图所示,轻质杠杆处于静止状态,请在图中画出力F1的力臂l1和阻力F2。
画最小力的一般步骤为:
(1)找支点;
(2)找力的作用点;
(3)连接支点和力的作用点;
(4)过力的作用点作连线的垂线,垂线即为最小力的方向。
类型二 最小力问题
3.如图是一根轻质杠杆,O为支点,请作出最小动力的示意图。
4.如图所示为一拉杆箱的示意图。将其视为杠杆,O为支点,B为重心,A为拉杆端点,请画出重力G的力臂l2及使拉杆箱在图示位置静止时的最小动力F。
滑轮组绕绳的关键点是判断绳的起点,最省力的绕法是从动滑轮的钩上开始绕绳,尽可能增加与动滑轮接触的绳子的股数。注意“奇动偶定”,即与动滑轮接触的绳子的股数为奇数时,从动滑轮的钩上开始绕绳;与动滑轮接触的绳子的股数为偶数时,从定滑轮的钩上开始绕绳。
类型三 滑轮组
5.如图所示,请画出滑轮组提起重物最省力时绳子的绕法。
6.如图所示,人要站在楼上提升重物,请在图中画出最省力的绕绳方法。
利用公式计算机械的效率
专项2
教你一招
1.使用机械使物体升高,有用功W有=Gh;使用机械使物体水平移动,
有用功W有=fs物。
2.使用机械,总功是利用机械所做的功W总=Fs或W总=Pt。
3.机械效率η=。
4.滑轮组提升重物机械效率的计算:
(1)η=、η=、η=这几个公式是通用公式;
(2)若不计摩擦和绳重,则有η=。
例: 如图所示,在水平地面上放着物体A,A与地面的接触面积为0.14 m2,对地面的压强为3 000 Pa,用滑轮组匀速提升物体A时,滑轮组的机械效率是84%,不计绳重和摩擦,g取10 N/kg。求:
(1)物体A的质量mA和动滑轮的质量m;
(2)用此滑轮组使物体A以0.2 m/s的速度匀速上升,在5 s的时间内,人拉力做的功是多少?
解:(1)A对地面的压力F压=pS=3 000 Pa×0.14 m2=420 N,
物体A的重力GA=F压=420 N,物体A的质量mA===42 kg。
用滑轮组匀速提升物体A时,不计绳重和摩擦,则滑轮组的机械效率
η===,即=84%,解得G轮=80 N,
动滑轮的质量m===8 kg。
(2)用此滑轮组使物体A以0.2 m/s的速度匀速上升5 s,
则物体A上升的高度h=vt=0.2 m/s×5 s=1 m,由图可知n=2,
则拉力端移动距离s=2h=2×1 m=2 m,不计绳重和摩擦,
则有nF=GA+G轮,即2F=420 N+80 N,解得F=250 N,
人拉力做的功W总=Fs=250 N×2 m=500 J。
例:以“‘荆歌’铁马,奔向未来”为主题的2023荆州马拉松3月26日在荆州体育中心
鸣枪起跑。在开赛场地建设过程中,工人利用长度L=3 m的斜面把质量为240 kg的重物匀速推到h=1 m高处,如图所示,工人所用推力F=1 000 N,g取10 N/kg。求:
(1)推力做的有用功;
(2)斜面的机械效率;
(3)工人将另一质量为300 kg的重物匀速推到同一高度,
为了省力,换用长度为5 m的斜面,此时重物与斜面
间的摩擦力与原来的摩擦力之比为6∶5,共用时20 s,
工人推力做功的功率。
解:(1)W有=mgh=240 kg×10 N/kg×1 m=2 400 J。
(2)W总=Fs=1 000 N×3 m=3 000 J,
η===80%。
(3)W额=W总-W有=3 000 J-2 400 J=600 J,f===200 N。
f'=f=×200 N=240 N,W有'=G'h=m'gh=3 000 J,
W额'=f's'=1 200 J,W总'=W有'+W额'=4 200 J,
P===210 W。
例:如图所示,某建筑工地上,工人通过固定在斜面顶端的滑轮组把工件匀速拉上斜面。已知斜面高h=6 m,长L=10 m,工人施加的拉力F=600 N,工件的质量m=250 kg,工件沿斜面上升的速度v=0.5 m/s。若不计工件和滑轮组长度,忽略绳和动滑轮重量及绳与滑轮间、滑轮与轮轴间的摩擦,g取10 N/kg。求:
(1)拉力F做功的功率P;
(2)整个装置的机械效率η;
(3)工件所受斜面的摩擦力f。
解:(1)v1=nv=3×0.5 m/s=1.5 m/s,P=Fv1=600 N×1.5 m/s=900 W。
(2)W=F×nL=600 N×3×10 m=1.8×104 J,
W1=Gh=mgh=250 kg×10 N/kg×6 m=1.5×104 J,
η===83.3%。
(3)W2=W-W1=1.8×104 J-1.5×104 J=3×103 J,
f===300 N。
利用杠杆平衡条件测密度
专项3
利用杠杆平衡条件测密度的思路:
利用直杆与刻度尺,运用杠杆平衡条件测物体的重力;再利用排水法可间接测得物体的体积,进而求出物体的密度。
(1)在实验前,杠杆静止在图甲所示的位置,此时杠杆处于 (填“平衡”或“不平衡”)状态;要使杠杆在水平位置平衡,应将平衡螺母向 调节,这样做的目的是 ,并消除杠杆自重对实验的影响;
(2)在溢水杯中装满水,如图乙所示,将石块缓慢浸没在水中,让溢出的水流入小桶A中,此时小桶A中水的体积 石块的体积;
例:如图所示的是“利用杠杆测量石块密度”的实验。(ρ水=1.0×103 kg/m3)
平衡
右
便于从杠杆上测量力臂
等于
(3)将石块从溢水杯中取出,擦干后放入另一相同小桶B中,将装有水和石块的A、B两个小桶分别挂在调好的杠杆两端,移动小桶在杠杆上的位置,直到杠杆在水平位置平衡,如图丙所示。此时小桶A、B的悬挂点距支点O分别为13 cm和5 cm,若不考虑小桶重力,则石块密度的测量值为 kg/m3。
2.6×103
【点拨】题图丙中,由杠杆平衡条件可得,
G石l1=G水l2,即m石gl1=m水gl2,ρ石V石gl1=ρ水V水gl2,ρ石V石l1=ρ水V水l2,
又溢出的水的体积等于石块的体积,即V石=V水,
则石块的密度ρ石=·ρ水=×1.0×103 kg/m3=2.6×103 kg/m3。
课后作业
十二章 简单杠杆
人教版 物理
1. 定义:
在力的作用下能绕着固定点转动的一根硬棒,这根硬棒就是杠杆。
(注意:杠杆可以是直的,也可以是弯曲的。)
2.认识杠杆的“五要素”
支 点:杠杆绕着转动的点O
动 力:使杠杆转动的力F1
阻 力:阻碍杠杆转动的力F2
动力臂:从支点O到动力F1作用线的距离l1
阻力臂:从支点O到阻力F2作用线的距离l2
F1
F2
l1
l2
一、杠杆
3.力臂的画法
以人用撬棒翘起物体为例——画出动力F1与阻力F2的力臂
注意:
(1)必要时要用虚线将力的作用线延长;
(2)力臂用双向箭头的实线,并标注力臂的名称;
(3)力臂与力的作用线一定要画“垂直符号”。
F1
F2
O
l1
l2
2.该实验需改变力和力臂来实现多次实验的目的:
避免偶然性,使实验结论具有普遍性。
二、杠杆的平衡条件
1.调节杠杆在水平位置平衡的目的:
3.杠杆的平衡条件是:
F1 l1 = F2 l2
(1)可以从杠杆上直接读出力臂,不用测量。
(2)可以消除杠杆自身的重力对实验结果的影响。
动力×动力臂=阻力×阻力臂
省力杠杆
等臂杠杆
省力杠杆
费力杠杆
省力杠杆
省力杠杆
“生活中的杠杆”,判断下面生活中常见的工具属于哪类杠杆?
想想议议
杠杆种类 力臂的关系 力的关系 特点 应用举例
省力杠杆 撬棒、起瓶器、手推车、夹钳等
费力杠杆 镊子、钓鱼竿、筷子、船桨等
等臂杠杆 天平、定滑轮等
L1>L2
F1<F2
省力费距离
F1>F2
费力省距离
L1=L2
F1=F2
既不省力也不省距离
L1<L2
杠杆的分类
滑轮:边缘有凹槽,能绕轴转动的小轮。
三、滑轮
1.实验探究:使用定滑轮的特点
①拉力与重力的大小关系:F=G,即使用定滑轮不省力。
②拉力的方向:可以改变。
③拉力(自由端)移动距离S绳与钩码上升高度h物的关系: 相等。
实验分析
定滑轮的特点:
不省力,不省距离,但可以改变力的方向。
定滑轮的实质:相当于一个能够连续转动的等臂杠杆。
定滑轮的实质
如图所示,定滑轮的轴心O为支点,动力臂l1与阻力臂l2都是滑轮的半径r。
由杠杆平衡的条件:F1l1=F2l2
即:Fl1=Gl2
力臂始终相等,则力相等
2.实验探究:使用动滑轮的特点。
注意:
用力缓慢拉动弹簧测力计竖直向上匀速运动。
动滑轮
①拉力与重力的关系:F<G,即使用动滑轮省力。若不计动滑轮的重力及摩擦力时,则拉力:F=G/2。
②拉力的方向:不能改变。
③拉力(绳末端)移动距离S绳与钩码上升高度h物的关系: S绳=2h物。
实验分析
使用动滑轮的特点:
能省力,但要费距离,且不能改变动力的方向。
支点在绳和轮相切的O处;拉力F1是动力,重物的拉力是阻力F2;动力臂L1是轮直径、动力臂L2是轮半径。
根据杠杆的平衡条件:F1l1=F2l2
l1= 2l2 ;
绳子自由端移动的距离S和物体升高的高度h:S=2h
动滑轮的实质
动滑轮的实质:相当于一个动力臂等于阻力臂2倍的省力杠杆。
(不计摩擦和动滑轮重)
O
A
F
l2 = R
l1= 2R
O
G
F
G
动滑轮两种常见情况的等量关系
(设物体做匀速运动,考虑滑轮自重,忽略摩擦)
F
F
2F=( G物 + G 动)
即 F
同一根绳子上的拉力大小相等
G动
G物
G动
G物
G物
F=2G物+G轮
3.滑轮组
定滑轮与动滑轮的组合叫滑轮组。
使用滑轮组既可以省力; 又可以改变力的方向。
分析判断滑轮组的省力与费距离的情况
G物
F1
F2
n=3
s=3h
不计动滑轮的重和摩擦:
计动滑轮的重和摩擦:
s=3h
F2
F1
G物
n=2
s=2h
不计动滑轮的重和摩擦:
计动滑轮的重和摩擦:
s=2h
结论:使用滑轮组省了力,但是费距离。
F
F
结论:
n为承担物重的绳子段数。
讨 论
5. 机械效率总是小于1的,通常用百分数表示。
1. 意义:
机械效率是反映机械做功性能的物理量。
2. 定义:
物理学中,将有用功跟总功的比值叫做机械效率。
3. 符号:
用“η”表示。
4. 公式:
η
=
W有
W总
在保证所做有用功一定的情况下,人们总是希望额外功越少越好。即额外功在总功中所占的比例越少越好。
总功:有用功与额外功之和。 (W总= W有+ W额)
四、机械效率
6.机械效率的三种类型
类型1· 滑轮组竖直提升重物
①有用功:
W有=Gh
②总 功:
W总=Fs
③机械效率:
④额外功:
W额= G动h
(不计绳重和摩擦)
s
h
η
=
W有
W总
=
Gh
Fs
=
G
nF
类型2·滑轮组水平拉动物体(不计滑轮及绳重)
①有用功:
W有= f s物
②总 功:
W总=Fs绳
③机械效率:
s绳
s物
f
η
=
W有
W总
=
f s物
Fs绳
=
f
nF
类型3·用斜面提升物体
①有用功:
W有=Gh
②总 功:
W总=Fs
③机械效率:
η
=
W有
W总
=
Gh
Fs
④额外功:
W额= f s
s
f
7.实验探究 测量滑轮组的机械效率
实验原理:
η
=
W有
W总
=
Gh
Fs
甲 乙
注意事项:
竖直向上缓慢(匀速)拉动测力计。
结论:动滑轮重一定时,物重越大,机械效率越高。
物重一定时,动滑轮越重,机械效率越低。
提高机械效率的方法:
改进滑轮结构,减轻动滑轮自重;
在机械承受的范围内,增加物重;
减小机械间的摩擦(加润滑油)。
杠杆、滑轮作图
专项1
画杠杆力臂的一般步骤为:首先找到力的作用线(过力的作用点沿力的方向画的一条直线),然后从支点向力的作用线作垂线,垂线段的长即为力臂。
类型一 力臂作图
1.用如图所示的装置来改变照明灯的高度,轻质杠杆ABO可绕O点转动,请在图中画出拉起杠杆的动力F的力臂l1及杠杆受到的阻力F′。
2.如图所示,轻质杠杆处于静止状态,请在图中画出力F1的力臂l1和阻力F2。
画最小力的一般步骤为:
(1)找支点;
(2)找力的作用点;
(3)连接支点和力的作用点;
(4)过力的作用点作连线的垂线,垂线即为最小力的方向。
类型二 最小力问题
3.如图是一根轻质杠杆,O为支点,请作出最小动力的示意图。
4.如图所示为一拉杆箱的示意图。将其视为杠杆,O为支点,B为重心,A为拉杆端点,请画出重力G的力臂l2及使拉杆箱在图示位置静止时的最小动力F。
滑轮组绕绳的关键点是判断绳的起点,最省力的绕法是从动滑轮的钩上开始绕绳,尽可能增加与动滑轮接触的绳子的股数。注意“奇动偶定”,即与动滑轮接触的绳子的股数为奇数时,从动滑轮的钩上开始绕绳;与动滑轮接触的绳子的股数为偶数时,从定滑轮的钩上开始绕绳。
类型三 滑轮组
5.如图所示,请画出滑轮组提起重物最省力时绳子的绕法。
6.如图所示,人要站在楼上提升重物,请在图中画出最省力的绕绳方法。
利用公式计算机械的效率
专项2
教你一招
1.使用机械使物体升高,有用功W有=Gh;使用机械使物体水平移动,
有用功W有=fs物。
2.使用机械,总功是利用机械所做的功W总=Fs或W总=Pt。
3.机械效率η=。
4.滑轮组提升重物机械效率的计算:
(1)η=、η=、η=这几个公式是通用公式;
(2)若不计摩擦和绳重,则有η=。
例: 如图所示,在水平地面上放着物体A,A与地面的接触面积为0.14 m2,对地面的压强为3 000 Pa,用滑轮组匀速提升物体A时,滑轮组的机械效率是84%,不计绳重和摩擦,g取10 N/kg。求:
(1)物体A的质量mA和动滑轮的质量m;
(2)用此滑轮组使物体A以0.2 m/s的速度匀速上升,在5 s的时间内,人拉力做的功是多少?
解:(1)A对地面的压力F压=pS=3 000 Pa×0.14 m2=420 N,
物体A的重力GA=F压=420 N,物体A的质量mA===42 kg。
用滑轮组匀速提升物体A时,不计绳重和摩擦,则滑轮组的机械效率
η===,即=84%,解得G轮=80 N,
动滑轮的质量m===8 kg。
(2)用此滑轮组使物体A以0.2 m/s的速度匀速上升5 s,
则物体A上升的高度h=vt=0.2 m/s×5 s=1 m,由图可知n=2,
则拉力端移动距离s=2h=2×1 m=2 m,不计绳重和摩擦,
则有nF=GA+G轮,即2F=420 N+80 N,解得F=250 N,
人拉力做的功W总=Fs=250 N×2 m=500 J。
例:以“‘荆歌’铁马,奔向未来”为主题的2023荆州马拉松3月26日在荆州体育中心
鸣枪起跑。在开赛场地建设过程中,工人利用长度L=3 m的斜面把质量为240 kg的重物匀速推到h=1 m高处,如图所示,工人所用推力F=1 000 N,g取10 N/kg。求:
(1)推力做的有用功;
(2)斜面的机械效率;
(3)工人将另一质量为300 kg的重物匀速推到同一高度,
为了省力,换用长度为5 m的斜面,此时重物与斜面
间的摩擦力与原来的摩擦力之比为6∶5,共用时20 s,
工人推力做功的功率。
解:(1)W有=mgh=240 kg×10 N/kg×1 m=2 400 J。
(2)W总=Fs=1 000 N×3 m=3 000 J,
η===80%。
(3)W额=W总-W有=3 000 J-2 400 J=600 J,f===200 N。
f'=f=×200 N=240 N,W有'=G'h=m'gh=3 000 J,
W额'=f's'=1 200 J,W总'=W有'+W额'=4 200 J,
P===210 W。
例:如图所示,某建筑工地上,工人通过固定在斜面顶端的滑轮组把工件匀速拉上斜面。已知斜面高h=6 m,长L=10 m,工人施加的拉力F=600 N,工件的质量m=250 kg,工件沿斜面上升的速度v=0.5 m/s。若不计工件和滑轮组长度,忽略绳和动滑轮重量及绳与滑轮间、滑轮与轮轴间的摩擦,g取10 N/kg。求:
(1)拉力F做功的功率P;
(2)整个装置的机械效率η;
(3)工件所受斜面的摩擦力f。
解:(1)v1=nv=3×0.5 m/s=1.5 m/s,P=Fv1=600 N×1.5 m/s=900 W。
(2)W=F×nL=600 N×3×10 m=1.8×104 J,
W1=Gh=mgh=250 kg×10 N/kg×6 m=1.5×104 J,
η===83.3%。
(3)W2=W-W1=1.8×104 J-1.5×104 J=3×103 J,
f===300 N。
利用杠杆平衡条件测密度
专项3
利用杠杆平衡条件测密度的思路:
利用直杆与刻度尺,运用杠杆平衡条件测物体的重力;再利用排水法可间接测得物体的体积,进而求出物体的密度。
(1)在实验前,杠杆静止在图甲所示的位置,此时杠杆处于 (填“平衡”或“不平衡”)状态;要使杠杆在水平位置平衡,应将平衡螺母向 调节,这样做的目的是 ,并消除杠杆自重对实验的影响;
(2)在溢水杯中装满水,如图乙所示,将石块缓慢浸没在水中,让溢出的水流入小桶A中,此时小桶A中水的体积 石块的体积;
例:如图所示的是“利用杠杆测量石块密度”的实验。(ρ水=1.0×103 kg/m3)
平衡
右
便于从杠杆上测量力臂
等于
(3)将石块从溢水杯中取出,擦干后放入另一相同小桶B中,将装有水和石块的A、B两个小桶分别挂在调好的杠杆两端,移动小桶在杠杆上的位置,直到杠杆在水平位置平衡,如图丙所示。此时小桶A、B的悬挂点距支点O分别为13 cm和5 cm,若不考虑小桶重力,则石块密度的测量值为 kg/m3。
2.6×103
【点拨】题图丙中,由杠杆平衡条件可得,
G石l1=G水l2,即m石gl1=m水gl2,ρ石V石gl1=ρ水V水gl2,ρ石V石l1=ρ水V水l2,
又溢出的水的体积等于石块的体积,即V石=V水,
则石块的密度ρ石=·ρ水=×1.0×103 kg/m3=2.6×103 kg/m3。
课后作业
