湖北省黄石市有色中学2023-2024学年九年级下学期2月收心考试数学试题(无答案)
文档属性
| 名称 | 湖北省黄石市有色中学2023-2024学年九年级下学期2月收心考试数学试题(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 281.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-13 00:00:00 | ||
图片预览

文档简介
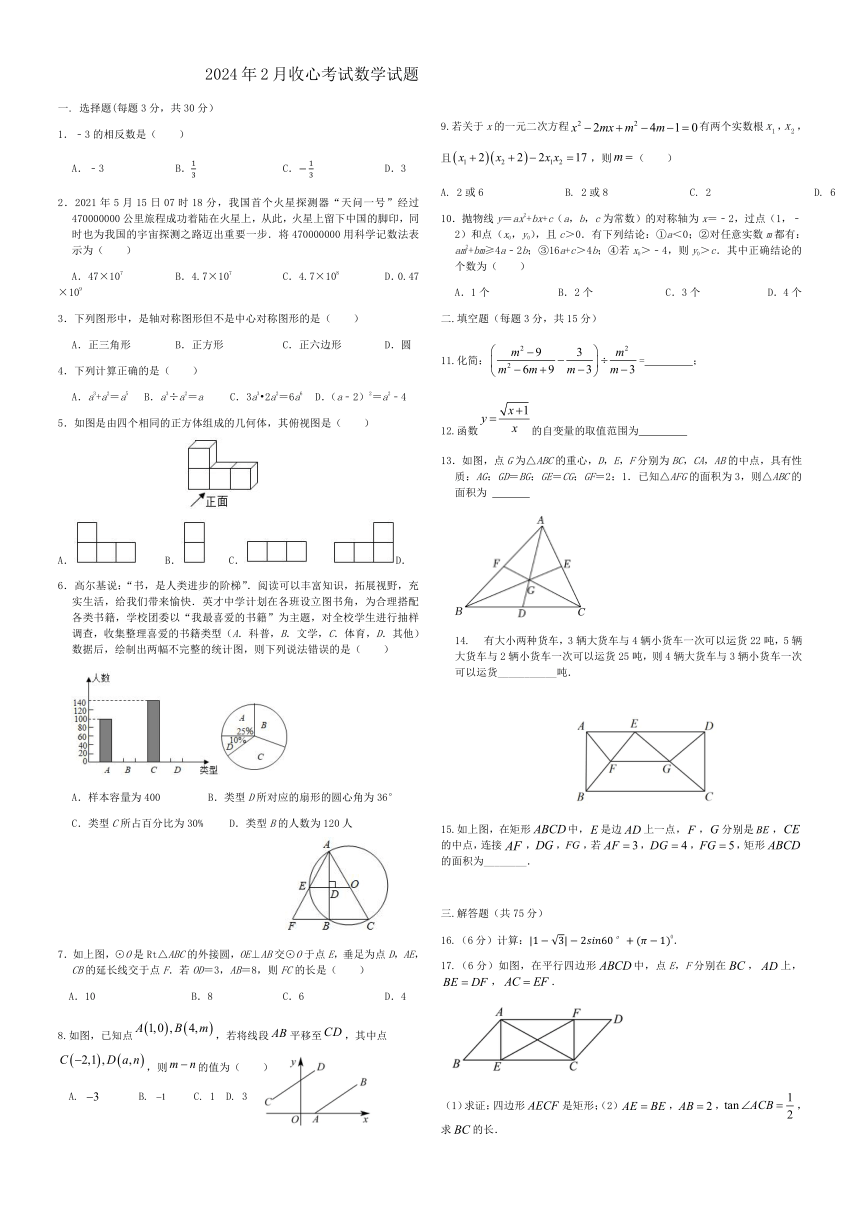
2024年2月收心考试数学试题
选择题(每题3分,共30分)
1.﹣3的相反数是( )
A.﹣3 B. C. D.3
2.2021年5月15日07时18分,我国首个火星探测器“天问一号”经过470000000公里旅程成功着陆在火星上,从此,火星上留下中国的脚印,同时也为我国的宇宙探测之路迈出重要一步.将470000000用科学记数法表示为( )
A.47×107 B.4.7×107 C.4.7×108 D.0.47×109
3.下列图形中,是轴对称图形但不是中心对称图形的是( )
A.正三角形 B.正方形 C.正六边形 D.圆
4.下列计算正确的是( )
A.a3+a2=a5 B.a3÷a2=a C.3a3 2a2=6a6 D.(a﹣2)2=a2﹣4
5.如图是由四个相同的正方体组成的几何体,其俯视图是( )
A. B. C. D.
6.高尔基说:“书,是人类进步的阶梯”.阅读可以丰富知识,拓展视野,充实生活,给我们带来愉快.英才中学计划在各班设立图书角,为合理搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对全校学生进行抽样调查,收集整理喜爱的书籍类型(A.科普,B.文学,C.体育,D.其他)数据后,绘制出两幅不完整的统计图,则下列说法错误的是( )
A.样本容量为400 B.类型D所对应的扇形的圆心角为36°
C.类型C所占百分比为30% D.类型B的人数为120人
7.如上图,⊙O是Rt△ABC的外接圆,OE⊥AB交⊙O于点E,垂足为点D,AE,CB的延长线交于点F.若OD=3,AB=8,则FC的长是( )
A.10 B.8 C.6 D.4
8.如图,已知点,若将线段平移至,其中点,则的值为( )
A. B. C. 1 D. 3
9.若关于x的一元二次方程有两个实数根,,且,则( )
A. 2或6 B. 2或8 C. 2 D. 6
10.抛物线y=ax2+bx+c(a,b,c为常数)的对称轴为x=﹣2,过点(1,﹣2)和点(x0,y0),且c>0.有下列结论:①a<0;②对任意实数m都有:am2+bm≥4a﹣2b;③16a+c>4b;④若x0>﹣4,则y0>c.其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
二.填空题(每题3分,共15分)
11.化简:= ;
12.函数的自变量的取值范围为
13.如图,点G为△ABC的重心,D,E,F分别为BC,CA,AB的中点,具有性质:AG:GD=BG:GE=CG:GF=2:1.已知△AFG的面积为3,则△ABC的面积为
有大小两种货车,3辆大货车与4辆小货车一次可以运货22吨,5辆大货车与2辆小货车一次可以运货25吨,则4辆大货车与3辆小货车一次可以运货___________吨.
15.如上图,在矩形中,是边上一点,,分别是,的中点,连接,,,若,,,矩形的面积为________.
三.解答题(共75分)
16.(6分)计算:0.
17.(6分)如图,在平行四边形中,点E,F分别在,上,,.
(1)求证:四边形是矩形;(2),,,求的长.
18.(6分)如图,在Rt△ABC中,∠ACB=90°,⊙O与BC,AC分别相切于点E,F,BO平分∠ABC,连接OA.(1)求证:AB是⊙O的切线;(2)若BE=AC=3,⊙O的半径是1,求图中阴影部分的面积.
19.(8分)为了了解学生对“新冠疫情防护知识”的应知应会程度,某校随机选取了20名学生“新冠疫情防护知识”的测评成绩,数据如表:
成绩/分 88 89 90 91 95 96 97 98 99
学生人数 2 1 a 3 2 1 3 2 1
数据表中有一个数因模糊不清用字母a表示.
(1)试确定a的值及测评成绩的平均数,并补全条形图;
(2)记测评成绩为x,学校规定:80≤x<90时,成绩为合格;90≤x<97时,成绩为良好;97≤x≤100时,成绩为优秀.求扇形统计图中m和n的值:
(3)从成绩为优秀的学生中随机抽取2人,求恰好1人得97分、1人得98分的概率.
20.(8分)小红同学在数学活动课中测量旗杆的高度,如图,已知测角仪的高度为1.58米,她在A点观测杆顶E的仰角为30°,接着朝旗杆方向前进20米到达C处,在D点观测旗杆顶端E的仰角为60°,求旗杆的高度.(结果保留小数点后一位)(参考数据:)
21.(8分)如图,已知一次函数与反比例函数的图象在第一、三象限分别交于,两点,连接,.
(1)求一次函数和反比例函数的解析式;
(2)求的面积
(3)直接写出时x的取值范围.
22.(10分)网络销售已经成为一种热门的销售方式,为了减少农产品的库存,黄冈市市长亲自在某网络平台上进行直播销售大别山牌板栗.为提高大家购买的积极性,直播时,板栗公司每天拿出2000元现金,作为红包发给购买者.已知该板栗的成本价格为6元,每日销售量与销售单价x(元)满足关系式:.经销售发现,销售单价不低于成本价格且不高于30元.当每日销售量不低于时,每千克成本将降低1元。设板栗公司销售该板栗的日获利为W(元).
(1)请求出日获利W与销售单价x之间的函数关系式
(2)当销售单价定为多少时,销售这种板栗日获利最大?最大利润为多少元?
(3)当元时,网络平台将向板栗公可收取a元的相关费用,若此时日获利的最大值为42100元,求a的值.
23.(11分)实践操作:第一步:如图1,将矩形纸片沿过点D的直线折叠,使点A落在上的点处,得到折痕,然后把纸片展平.第二步:如图2,将图1中的矩形纸片沿过点E的直线折叠,点C恰好落在上的点处,点B落在点处,得到折痕,交于点M,交于点N,再把纸片展平.
问题解决:
(1)如图1,填空:四边形的形状是_____________________;
(2)如图2,线段与是否相等?若相等,请给出证明;若不等,请说明理由;
(3)如图2,若,求的值.
24.(12分)如图,在平面直角坐标系中,抛物线与x轴交于两点,与y轴交于点.
(1)求此抛物线的解析式;
(2)已知抛物线上有一点,其中,若,求的值;
(3)若点D,E分别是线段,上的动点,且,求的最小值.
选择题(每题3分,共30分)
1.﹣3的相反数是( )
A.﹣3 B. C. D.3
2.2021年5月15日07时18分,我国首个火星探测器“天问一号”经过470000000公里旅程成功着陆在火星上,从此,火星上留下中国的脚印,同时也为我国的宇宙探测之路迈出重要一步.将470000000用科学记数法表示为( )
A.47×107 B.4.7×107 C.4.7×108 D.0.47×109
3.下列图形中,是轴对称图形但不是中心对称图形的是( )
A.正三角形 B.正方形 C.正六边形 D.圆
4.下列计算正确的是( )
A.a3+a2=a5 B.a3÷a2=a C.3a3 2a2=6a6 D.(a﹣2)2=a2﹣4
5.如图是由四个相同的正方体组成的几何体,其俯视图是( )
A. B. C. D.
6.高尔基说:“书,是人类进步的阶梯”.阅读可以丰富知识,拓展视野,充实生活,给我们带来愉快.英才中学计划在各班设立图书角,为合理搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对全校学生进行抽样调查,收集整理喜爱的书籍类型(A.科普,B.文学,C.体育,D.其他)数据后,绘制出两幅不完整的统计图,则下列说法错误的是( )
A.样本容量为400 B.类型D所对应的扇形的圆心角为36°
C.类型C所占百分比为30% D.类型B的人数为120人
7.如上图,⊙O是Rt△ABC的外接圆,OE⊥AB交⊙O于点E,垂足为点D,AE,CB的延长线交于点F.若OD=3,AB=8,则FC的长是( )
A.10 B.8 C.6 D.4
8.如图,已知点,若将线段平移至,其中点,则的值为( )
A. B. C. 1 D. 3
9.若关于x的一元二次方程有两个实数根,,且,则( )
A. 2或6 B. 2或8 C. 2 D. 6
10.抛物线y=ax2+bx+c(a,b,c为常数)的对称轴为x=﹣2,过点(1,﹣2)和点(x0,y0),且c>0.有下列结论:①a<0;②对任意实数m都有:am2+bm≥4a﹣2b;③16a+c>4b;④若x0>﹣4,则y0>c.其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
二.填空题(每题3分,共15分)
11.化简:= ;
12.函数的自变量的取值范围为
13.如图,点G为△ABC的重心,D,E,F分别为BC,CA,AB的中点,具有性质:AG:GD=BG:GE=CG:GF=2:1.已知△AFG的面积为3,则△ABC的面积为
有大小两种货车,3辆大货车与4辆小货车一次可以运货22吨,5辆大货车与2辆小货车一次可以运货25吨,则4辆大货车与3辆小货车一次可以运货___________吨.
15.如上图,在矩形中,是边上一点,,分别是,的中点,连接,,,若,,,矩形的面积为________.
三.解答题(共75分)
16.(6分)计算:0.
17.(6分)如图,在平行四边形中,点E,F分别在,上,,.
(1)求证:四边形是矩形;(2),,,求的长.
18.(6分)如图,在Rt△ABC中,∠ACB=90°,⊙O与BC,AC分别相切于点E,F,BO平分∠ABC,连接OA.(1)求证:AB是⊙O的切线;(2)若BE=AC=3,⊙O的半径是1,求图中阴影部分的面积.
19.(8分)为了了解学生对“新冠疫情防护知识”的应知应会程度,某校随机选取了20名学生“新冠疫情防护知识”的测评成绩,数据如表:
成绩/分 88 89 90 91 95 96 97 98 99
学生人数 2 1 a 3 2 1 3 2 1
数据表中有一个数因模糊不清用字母a表示.
(1)试确定a的值及测评成绩的平均数,并补全条形图;
(2)记测评成绩为x,学校规定:80≤x<90时,成绩为合格;90≤x<97时,成绩为良好;97≤x≤100时,成绩为优秀.求扇形统计图中m和n的值:
(3)从成绩为优秀的学生中随机抽取2人,求恰好1人得97分、1人得98分的概率.
20.(8分)小红同学在数学活动课中测量旗杆的高度,如图,已知测角仪的高度为1.58米,她在A点观测杆顶E的仰角为30°,接着朝旗杆方向前进20米到达C处,在D点观测旗杆顶端E的仰角为60°,求旗杆的高度.(结果保留小数点后一位)(参考数据:)
21.(8分)如图,已知一次函数与反比例函数的图象在第一、三象限分别交于,两点,连接,.
(1)求一次函数和反比例函数的解析式;
(2)求的面积
(3)直接写出时x的取值范围.
22.(10分)网络销售已经成为一种热门的销售方式,为了减少农产品的库存,黄冈市市长亲自在某网络平台上进行直播销售大别山牌板栗.为提高大家购买的积极性,直播时,板栗公司每天拿出2000元现金,作为红包发给购买者.已知该板栗的成本价格为6元,每日销售量与销售单价x(元)满足关系式:.经销售发现,销售单价不低于成本价格且不高于30元.当每日销售量不低于时,每千克成本将降低1元。设板栗公司销售该板栗的日获利为W(元).
(1)请求出日获利W与销售单价x之间的函数关系式
(2)当销售单价定为多少时,销售这种板栗日获利最大?最大利润为多少元?
(3)当元时,网络平台将向板栗公可收取a元的相关费用,若此时日获利的最大值为42100元,求a的值.
23.(11分)实践操作:第一步:如图1,将矩形纸片沿过点D的直线折叠,使点A落在上的点处,得到折痕,然后把纸片展平.第二步:如图2,将图1中的矩形纸片沿过点E的直线折叠,点C恰好落在上的点处,点B落在点处,得到折痕,交于点M,交于点N,再把纸片展平.
问题解决:
(1)如图1,填空:四边形的形状是_____________________;
(2)如图2,线段与是否相等?若相等,请给出证明;若不等,请说明理由;
(3)如图2,若,求的值.
24.(12分)如图,在平面直角坐标系中,抛物线与x轴交于两点,与y轴交于点.
(1)求此抛物线的解析式;
(2)已知抛物线上有一点,其中,若,求的值;
(3)若点D,E分别是线段,上的动点,且,求的最小值.
同课章节目录
