17.3一次函数之二课堂实录
图片预览

文档简介
八年级(华东师大)§17.3一次函数之二课堂实录
教学目标:1、知识与技能目标:会正确画出一次函数的图象,会求一次函数的图象与坐标轴的交点,探讨一些基本的性质。
2、过程与方法目标:通过学生积极参与画图,思考、分析,总结出又快又好的画出一次函数的图象的方法,并能利用一些基本的性质解决问题。
3、情感与态度目标:学生通过积极参与感受学习的快乐。
教学重点:一次函数的图象的画法,与坐标轴的交点的求法。
教学难点:与坐标轴的交点的求法的理解及其性质的简单应用。
教学方法:讲练结合
教学过程:
复习提问:一次函数的一般式是什么?
生:y=kx+b(k、b是常数,k≠0)
问:正比例函数是什么?
y=kx (k是常数,k≠0)
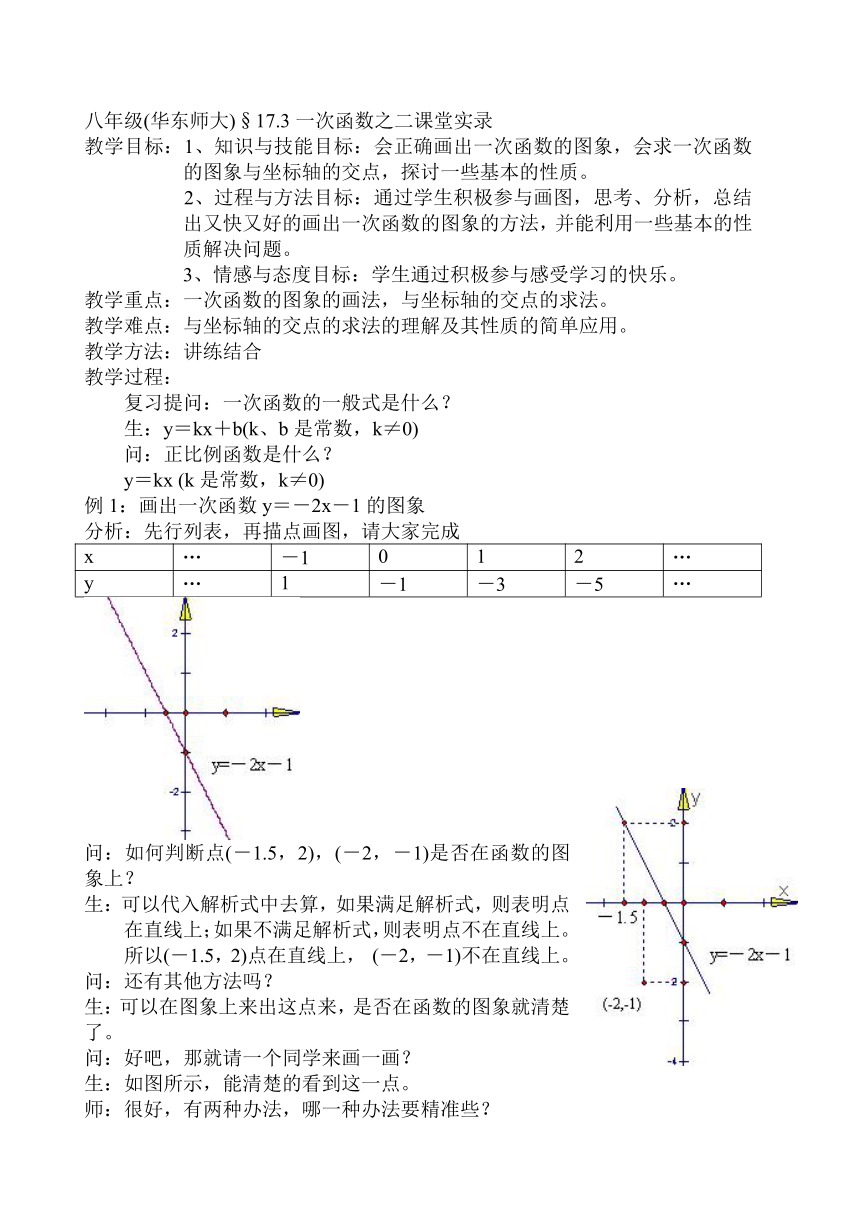
例1:画出一次函数y=-2x-1的图象
分析:先行列表,再描点画图,请大家完成
x … -1 0 1 2 …
y … 1 -1 -3 -5 …
问:如何判断点(-1.5,2),(-2,-1)是否在函数的图象上?
生:可以代入解析式中去算,如果满足解析式,则表明点在直线上;如果不满足解析式,则表明点不在直线上。所以(-1.5,2)点在直线上, (-2,-1)不在直线上。
问:还有其他方法吗?
生:可以在图象上来出这点来,是否在函数的图象就清楚了。
问:好吧,那就请一个同学来画一画?
生:如图所示,能清楚的看到这一点。
师:很好,有两种办法,哪一种办法要精准些?
生:计算的方法,画的方法有误差。
师:已知y=-2,1时,如何利用图象,分别求出其对应的x的值啊?
生:代入进去算不就完了吗?
师:当然可以,而且还很省事,但请看清楚我这里要利用图象求。谁到黑板上来画?
王磊:先找到y=-2,1分别向y轴做垂线,交图象上的点,再通过这个点向x轴做垂线,对应的x轴坐标上的值就是它的x的对应值。
师:这个做法是正确的,呵呵!看来难不倒大家哈,再来一个,如何利用图象求x=-2,-1的值?
生众:这不和刚才一样吗?只是先在横轴找到-2,-1的点,向x轴做垂线,与图象相交,再通过交点向y轴做垂线,对应的y的值是要求的。
师:很好,其实图象上一个点与其坐标是一一对应的,已知图象(或解析式),①横坐标;②纵坐标;③图象上的点,已知这三个当中的任何一个都能求出其余的两个来。
问:通过前面画一次函数的图象和刚才画的图象,你能归纳出一次函数的图象是什么样吗?
生:是一条直线。
师:确实是一条直线。既然是一条直线,我们就有想法,有什么样的想法?
生:两点确定一条直线,只需要画两个点就可以了。
师:不错,不错的,这么模糊的问题你们都能回答啊!现在我想问的是找哪两点最便捷呢?
生:取整数吧,比如1,0,-1等等。
师(这不是我期望的答案,看来得继续引导了):你们的取法当然也说得通,但你们的取法有此图中是否好画呢?误差是否大呢?考虑了这些没有?
生:画图描点时,要做两条虚线?
师:就是因为这两条虚线,会产生更大的误差,我们的想法是能不能不画这两条虚线,看看有什么好办法?
生:在坐标轴上取点。
师:就等你们说这句话了。我也是这样认为的。请看看这个图象与x、y轴的交点如何求?
生:(0.5,0),(0,-1)
师:你们是直接通过图象看出来的,我是说的如何求,你们又没有仔细听我的问题吧,在画图象前要把这两点先求出来啊,然后再坐标轴上描出这两点,用尺子一画就完事了,谁来说,如何求?
徐林:因为这是图象与x、y轴的交点,其纵、横坐标分别为0,代入即可求出相应的另一个坐标。
师:刚才徐林的回答是非常正确的,也就是此时在坐标轴上,要结合坐标轴上的点的坐标有什么样的特点来进行思考。因此其答案是:(0.5,0),(0,-1)。
师:请思考y=kx+b与y轴的交点是___;与x轴的交点是___。
生:与y轴的交点,此时x=0,代入有y=b,所以(0,b)是与y轴的交点的坐标;
生:与x轴的交点,此时y=0,代入有x=-,所以(-,0)是与x轴的交点的坐标;
检验一下刚才学习的效果,请完成练习P47
4. 填空:
(1)直线y=4x-3过点(___,0)、(0,___);
(2)直线过点(___,0)、(0,___).
师:以后画一次函数的图象就很省事了:
x 0
y 0
填上两个空格,描出两点,用尺子一画就完事了。
(生皆高兴)
那来练习画两个。
例2:在同一直角坐标系内画出以下四个函数的图象。
①y=2x-1;② y=2x+1;③y=-2x-1; ④y=2x。
①
x 0 0.5
y -1 0
②
x 0 -0.5
y 1 0
③
x 0 -0.5
y -1 0
④请大家想一想正比例函数的点如何取呢?横坐标可取0,1
x 0 1
y 0 0.5
生:①②④三条是平行的。
师:同学们的观察不错,我也发现了这三条是平行的,其图象的平行,必然是由解析式中的共同点所决定的?请思考你觉得是什么导致了他们平行?
生:他们的k值是相同的。
师:是正确的,有这样的结论:
已知直线l1:y=k1x+b1;l2:y=k2x+b2,且l1∥l2,有什么结论?
生:k1=k2。
师:能否由k1=k2得出l1∥l2?
生:可以。
结论:l1:y=k1x+b1;l2:y=k2x+b2,且l1∥l2 k1=k2。
练习题:
问:已知直线l1:y=3x-7,l2:y=2x+5.5有何关系?为什么?
生:平行。因为其k值是相同的。
问:l1:y=-x+1,l2:y=kx-7且l1∥l2,则k=___。
生:k=-。是由刚才的定理得来的。
师:请观察①②④③与y轴的交点的纵坐标与解析式中的什么有关?
生:与b有关,交点的纵坐标就是b的值。b是1就过1那一点,b是-1就过-1那一点。
师:这么肯定吗?看第④条没有b怎么过原点呢?
生:这还不简单,b=0,刚才过原点0啊?!
师:原来是这样,看来你们的发现是没错的。因为前面我们就已经计算出了每一条一次函数的图象都过(0,b)这一点。这就是当然的了。(k的正负,函数的增减,b的正负与y轴的交点间的更进一步的关系就留在下节课去了,得出性质后集中练习,本节课就完成本节课的内容了……)
师:这三条直线是平行的,能否看成是由另一条直线的平移得来的?
生:能够。
师:①是由④如何平移得到的?
生:向下平移一个单位长度得来的。
师:其解析式发生了怎样的变化?
生:b处减1。
师:②是由如何④平移得到的?
生:向上平移一个单位长度得来的。
师:其解析式发生了怎样的变化?
生:b处加1
师:②是由如何①平移得到的?
生:向上平移两个单位长度得来的。
师:其解析式发生了怎样的变化?
生:把前者的b加2即可。
师:你能否归纳出一次函数的上下平移的规律?
刘海波:把一条直线向上平移多少个单位长度,就在b的位置加上多少;反之把一条直线向下平移多少个单位长度,就在b的位置减去多少。
师:这个归纳是很好的,我们还要把它式子化。
把l1:y=k1x+b1向上平移m(m>0)个单位,则得到的解析式为l2:y=k1x+b1+m;y=k1x+b1向下平移m(m>0)个单位,则得到的解析式为l2:y=k1x+b1-m;
师:你们能否用四个字来说明他们的规律?
生:上加下减。
师:能干哦!与我想的一模一样。
请完成下面的练习:
P42练习2:
2.(1)将直线y=3x向下平移2个单位,得到直线_____________________;
(2)将直线y=-x-5向上平移5个单位,得到直线_____________________.
(此时下课铃声响起)
生:(1)为y=3x-2
(2)为y=-x.
课外思考题:
向左平移m个单位长度与向右平移m个单位长度的的解析式会发生怎样的变化?
教学目标:1、知识与技能目标:会正确画出一次函数的图象,会求一次函数的图象与坐标轴的交点,探讨一些基本的性质。
2、过程与方法目标:通过学生积极参与画图,思考、分析,总结出又快又好的画出一次函数的图象的方法,并能利用一些基本的性质解决问题。
3、情感与态度目标:学生通过积极参与感受学习的快乐。
教学重点:一次函数的图象的画法,与坐标轴的交点的求法。
教学难点:与坐标轴的交点的求法的理解及其性质的简单应用。
教学方法:讲练结合
教学过程:
复习提问:一次函数的一般式是什么?
生:y=kx+b(k、b是常数,k≠0)
问:正比例函数是什么?
y=kx (k是常数,k≠0)
例1:画出一次函数y=-2x-1的图象
分析:先行列表,再描点画图,请大家完成
x … -1 0 1 2 …
y … 1 -1 -3 -5 …
问:如何判断点(-1.5,2),(-2,-1)是否在函数的图象上?
生:可以代入解析式中去算,如果满足解析式,则表明点在直线上;如果不满足解析式,则表明点不在直线上。所以(-1.5,2)点在直线上, (-2,-1)不在直线上。
问:还有其他方法吗?
生:可以在图象上来出这点来,是否在函数的图象就清楚了。
问:好吧,那就请一个同学来画一画?
生:如图所示,能清楚的看到这一点。
师:很好,有两种办法,哪一种办法要精准些?
生:计算的方法,画的方法有误差。
师:已知y=-2,1时,如何利用图象,分别求出其对应的x的值啊?
生:代入进去算不就完了吗?
师:当然可以,而且还很省事,但请看清楚我这里要利用图象求。谁到黑板上来画?
王磊:先找到y=-2,1分别向y轴做垂线,交图象上的点,再通过这个点向x轴做垂线,对应的x轴坐标上的值就是它的x的对应值。
师:这个做法是正确的,呵呵!看来难不倒大家哈,再来一个,如何利用图象求x=-2,-1的值?
生众:这不和刚才一样吗?只是先在横轴找到-2,-1的点,向x轴做垂线,与图象相交,再通过交点向y轴做垂线,对应的y的值是要求的。
师:很好,其实图象上一个点与其坐标是一一对应的,已知图象(或解析式),①横坐标;②纵坐标;③图象上的点,已知这三个当中的任何一个都能求出其余的两个来。
问:通过前面画一次函数的图象和刚才画的图象,你能归纳出一次函数的图象是什么样吗?
生:是一条直线。
师:确实是一条直线。既然是一条直线,我们就有想法,有什么样的想法?
生:两点确定一条直线,只需要画两个点就可以了。
师:不错,不错的,这么模糊的问题你们都能回答啊!现在我想问的是找哪两点最便捷呢?
生:取整数吧,比如1,0,-1等等。
师(这不是我期望的答案,看来得继续引导了):你们的取法当然也说得通,但你们的取法有此图中是否好画呢?误差是否大呢?考虑了这些没有?
生:画图描点时,要做两条虚线?
师:就是因为这两条虚线,会产生更大的误差,我们的想法是能不能不画这两条虚线,看看有什么好办法?
生:在坐标轴上取点。
师:就等你们说这句话了。我也是这样认为的。请看看这个图象与x、y轴的交点如何求?
生:(0.5,0),(0,-1)
师:你们是直接通过图象看出来的,我是说的如何求,你们又没有仔细听我的问题吧,在画图象前要把这两点先求出来啊,然后再坐标轴上描出这两点,用尺子一画就完事了,谁来说,如何求?
徐林:因为这是图象与x、y轴的交点,其纵、横坐标分别为0,代入即可求出相应的另一个坐标。
师:刚才徐林的回答是非常正确的,也就是此时在坐标轴上,要结合坐标轴上的点的坐标有什么样的特点来进行思考。因此其答案是:(0.5,0),(0,-1)。
师:请思考y=kx+b与y轴的交点是___;与x轴的交点是___。
生:与y轴的交点,此时x=0,代入有y=b,所以(0,b)是与y轴的交点的坐标;
生:与x轴的交点,此时y=0,代入有x=-,所以(-,0)是与x轴的交点的坐标;
检验一下刚才学习的效果,请完成练习P47
4. 填空:
(1)直线y=4x-3过点(___,0)、(0,___);
(2)直线过点(___,0)、(0,___).
师:以后画一次函数的图象就很省事了:
x 0
y 0
填上两个空格,描出两点,用尺子一画就完事了。
(生皆高兴)
那来练习画两个。
例2:在同一直角坐标系内画出以下四个函数的图象。
①y=2x-1;② y=2x+1;③y=-2x-1; ④y=2x。
①
x 0 0.5
y -1 0
②
x 0 -0.5
y 1 0
③
x 0 -0.5
y -1 0
④请大家想一想正比例函数的点如何取呢?横坐标可取0,1
x 0 1
y 0 0.5
生:①②④三条是平行的。
师:同学们的观察不错,我也发现了这三条是平行的,其图象的平行,必然是由解析式中的共同点所决定的?请思考你觉得是什么导致了他们平行?
生:他们的k值是相同的。
师:是正确的,有这样的结论:
已知直线l1:y=k1x+b1;l2:y=k2x+b2,且l1∥l2,有什么结论?
生:k1=k2。
师:能否由k1=k2得出l1∥l2?
生:可以。
结论:l1:y=k1x+b1;l2:y=k2x+b2,且l1∥l2 k1=k2。
练习题:
问:已知直线l1:y=3x-7,l2:y=2x+5.5有何关系?为什么?
生:平行。因为其k值是相同的。
问:l1:y=-x+1,l2:y=kx-7且l1∥l2,则k=___。
生:k=-。是由刚才的定理得来的。
师:请观察①②④③与y轴的交点的纵坐标与解析式中的什么有关?
生:与b有关,交点的纵坐标就是b的值。b是1就过1那一点,b是-1就过-1那一点。
师:这么肯定吗?看第④条没有b怎么过原点呢?
生:这还不简单,b=0,刚才过原点0啊?!
师:原来是这样,看来你们的发现是没错的。因为前面我们就已经计算出了每一条一次函数的图象都过(0,b)这一点。这就是当然的了。(k的正负,函数的增减,b的正负与y轴的交点间的更进一步的关系就留在下节课去了,得出性质后集中练习,本节课就完成本节课的内容了……)
师:这三条直线是平行的,能否看成是由另一条直线的平移得来的?
生:能够。
师:①是由④如何平移得到的?
生:向下平移一个单位长度得来的。
师:其解析式发生了怎样的变化?
生:b处减1。
师:②是由如何④平移得到的?
生:向上平移一个单位长度得来的。
师:其解析式发生了怎样的变化?
生:b处加1
师:②是由如何①平移得到的?
生:向上平移两个单位长度得来的。
师:其解析式发生了怎样的变化?
生:把前者的b加2即可。
师:你能否归纳出一次函数的上下平移的规律?
刘海波:把一条直线向上平移多少个单位长度,就在b的位置加上多少;反之把一条直线向下平移多少个单位长度,就在b的位置减去多少。
师:这个归纳是很好的,我们还要把它式子化。
把l1:y=k1x+b1向上平移m(m>0)个单位,则得到的解析式为l2:y=k1x+b1+m;y=k1x+b1向下平移m(m>0)个单位,则得到的解析式为l2:y=k1x+b1-m;
师:你们能否用四个字来说明他们的规律?
生:上加下减。
师:能干哦!与我想的一模一样。
请完成下面的练习:
P42练习2:
2.(1)将直线y=3x向下平移2个单位,得到直线_____________________;
(2)将直线y=-x-5向上平移5个单位,得到直线_____________________.
(此时下课铃声响起)
生:(1)为y=3x-2
(2)为y=-x.
课外思考题:
向左平移m个单位长度与向右平移m个单位长度的的解析式会发生怎样的变化?
