第十章 三角形的有关证明 专题5 角平分线四大模型(含答案)
文档属性
| 名称 | 第十章 三角形的有关证明 专题5 角平分线四大模型(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-13 21:23:44 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十章 三角形的有关证明
专题5 角平分线四大模型
模型一 过角平分线上的点向两边作垂线
如图,P 是 的平分线上一点,过点 P作 于点 A, 于点 B.结论:
【模型分析】 利用角平分线的性质,向角的一边或两边作垂线,构造边的垂线,得到两个全等三角形.
1.如图,在 中,∠C=90°,AD 平分∠CAB,BC=8cm,BD=5cm ,那么点 D到直线 AB的距离是__________cm.
2.如图,已知 求证:AP 平分
模型二 截取构造对称全等
如图,P是的平分线上一点,点A是射线OM上任意一点,在ON上截取OA,连接 PB.结论:
【模型分析】利用角平分线的对称性,在角的两边构造对称全等三角形.
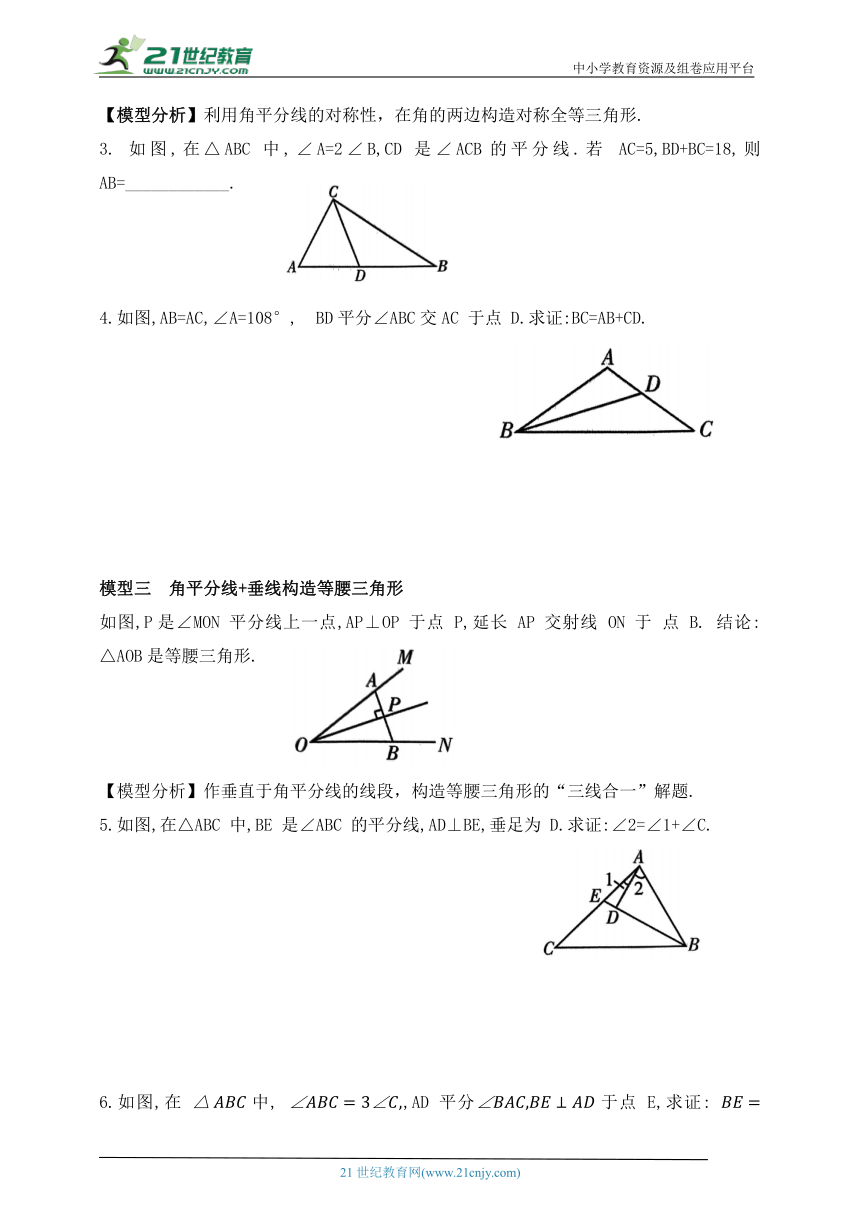
3. 如图,在△ABC 中,∠A=2∠B,CD 是∠ACB的平分线.若 AC=5,BD+BC=18,则AB=____________.
4.如图,AB=AC,∠A=108°, BD平分∠ABC交AC 于点 D.求证:BC=AB+CD.
模型三 角平分线+垂线构造等腰三角形
如图,P是∠MON 平分线上一点,AP⊥OP 于点 P,延长 AP 交射线 ON 于 点 B. 结论: △AOB是等腰三角形.
【模型分析】作垂直于角平分线的线段,构造等腰三角形的“三线合一”解题.
5.如图,在△ABC 中,BE 是∠ABC 的平分线,AD⊥BE,垂足为 D.求证:∠2=∠1+∠C.
6.如图,在 中, ,AD 平分于点 E,求证:
模型四 角平分线+平行线
如图,P 是 平分线上一点,过点 P 作∥交 OM 于点 Q.
结论: 是等腰三角形.
【模型分析】有角平分线无平行时构造平行,可简记为“角平分线+平行线,等腰必呈现”.
7.如图,在 中, 和 的平分线相交于点P,过点 P 作 ∥BC 交 AB 于点 D,交 AC 于点E.若 则线段DE 的长是__________.
8.如图, P 为 平分线上一点, 于点 D,∥交 OM 于点 E.若求 PD的长.
参考答案
1.3
2.证明:如图,过点 P 作PD⊥AB 的延长线于点D,PE⊥BC 于点E,PF⊥AC 的延长线于点F.
∵∠1=∠2,PD⊥AB,PE⊥BC,∴PD=PE,同理 PF=PE,∴PD=PF.
又∵PD⊥AB,PF⊥AC,∴AP平分∠BAC.
3.13
4.证明:在线段 BC上截取BE=BA,连接 DE,如图.
∵BD平分
在△ABD和△EBD中
∴△ABD≌△EBD(SAS),∴∠BED=∠A=108°,∠ADB=∠EDB.
又∵AB=AC,∠A=108°, =36°,
∴∠ABD=∠EBD=18°,∴∠ADB=∠EDB=180°-18°-108°=54°,
72°,
∴∠DEC=180°-∠DEB=180°-108°=72°,∴∠CDE=∠DEC,∴CD=CE,
∴BC=BE+EC=AB+CD.
5.证明:如图,延长AD 交 BC 于点F.
∵BE 是∠ABC的平分线,AD⊥BE,∴△ABF是等腰三角形,∠2=∠AFB.
∵∠AFB=∠1+∠C,∴∠2=∠1+∠C.
6.证明:如图,延长BE 交 AC 于点F.
∵BF⊥AD,AD平分∠BAC,∴△ABF是等腰三角形,∴∠ABF=∠AFB,AB=AF,BE=EF.
∵∠C+∠CBF=∠AFB=∠ABF,∠ABF+∠CBF=∠ABC=3∠C,
∴∠C+2∠CBF=3∠C,∴∠CBF=∠C,∴BF=CF,
∵CF=AC-AF=AC-AB,
7.10
8.解:过点 P 作PC⊥OM 于点C,如图.
∵PE∥ON,∴∠EPO=∠POD.
∵OP 是∠MON 的平分线,PD⊥ON,PC⊥OM,∴∠COP=∠DOP,PC=PD,
的长为6 cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十章 三角形的有关证明
专题5 角平分线四大模型
模型一 过角平分线上的点向两边作垂线
如图,P 是 的平分线上一点,过点 P作 于点 A, 于点 B.结论:
【模型分析】 利用角平分线的性质,向角的一边或两边作垂线,构造边的垂线,得到两个全等三角形.
1.如图,在 中,∠C=90°,AD 平分∠CAB,BC=8cm,BD=5cm ,那么点 D到直线 AB的距离是__________cm.
2.如图,已知 求证:AP 平分
模型二 截取构造对称全等
如图,P是的平分线上一点,点A是射线OM上任意一点,在ON上截取OA,连接 PB.结论:
【模型分析】利用角平分线的对称性,在角的两边构造对称全等三角形.
3. 如图,在△ABC 中,∠A=2∠B,CD 是∠ACB的平分线.若 AC=5,BD+BC=18,则AB=____________.
4.如图,AB=AC,∠A=108°, BD平分∠ABC交AC 于点 D.求证:BC=AB+CD.
模型三 角平分线+垂线构造等腰三角形
如图,P是∠MON 平分线上一点,AP⊥OP 于点 P,延长 AP 交射线 ON 于 点 B. 结论: △AOB是等腰三角形.
【模型分析】作垂直于角平分线的线段,构造等腰三角形的“三线合一”解题.
5.如图,在△ABC 中,BE 是∠ABC 的平分线,AD⊥BE,垂足为 D.求证:∠2=∠1+∠C.
6.如图,在 中, ,AD 平分于点 E,求证:
模型四 角平分线+平行线
如图,P 是 平分线上一点,过点 P 作∥交 OM 于点 Q.
结论: 是等腰三角形.
【模型分析】有角平分线无平行时构造平行,可简记为“角平分线+平行线,等腰必呈现”.
7.如图,在 中, 和 的平分线相交于点P,过点 P 作 ∥BC 交 AB 于点 D,交 AC 于点E.若 则线段DE 的长是__________.
8.如图, P 为 平分线上一点, 于点 D,∥交 OM 于点 E.若求 PD的长.
参考答案
1.3
2.证明:如图,过点 P 作PD⊥AB 的延长线于点D,PE⊥BC 于点E,PF⊥AC 的延长线于点F.
∵∠1=∠2,PD⊥AB,PE⊥BC,∴PD=PE,同理 PF=PE,∴PD=PF.
又∵PD⊥AB,PF⊥AC,∴AP平分∠BAC.
3.13
4.证明:在线段 BC上截取BE=BA,连接 DE,如图.
∵BD平分
在△ABD和△EBD中
∴△ABD≌△EBD(SAS),∴∠BED=∠A=108°,∠ADB=∠EDB.
又∵AB=AC,∠A=108°, =36°,
∴∠ABD=∠EBD=18°,∴∠ADB=∠EDB=180°-18°-108°=54°,
72°,
∴∠DEC=180°-∠DEB=180°-108°=72°,∴∠CDE=∠DEC,∴CD=CE,
∴BC=BE+EC=AB+CD.
5.证明:如图,延长AD 交 BC 于点F.
∵BE 是∠ABC的平分线,AD⊥BE,∴△ABF是等腰三角形,∠2=∠AFB.
∵∠AFB=∠1+∠C,∴∠2=∠1+∠C.
6.证明:如图,延长BE 交 AC 于点F.
∵BF⊥AD,AD平分∠BAC,∴△ABF是等腰三角形,∴∠ABF=∠AFB,AB=AF,BE=EF.
∵∠C+∠CBF=∠AFB=∠ABF,∠ABF+∠CBF=∠ABC=3∠C,
∴∠C+2∠CBF=3∠C,∴∠CBF=∠C,∴BF=CF,
∵CF=AC-AF=AC-AB,
7.10
8.解:过点 P 作PC⊥OM 于点C,如图.
∵PE∥ON,∴∠EPO=∠POD.
∵OP 是∠MON 的平分线,PD⊥ON,PC⊥OM,∴∠COP=∠DOP,PC=PD,
的长为6 cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
