第一单元 圆柱与圆锥(试题)--2023-2024-学年北师大版数学六年级下册(含答案)
文档属性
| 名称 | 第一单元 圆柱与圆锥(试题)--2023-2024-学年北师大版数学六年级下册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 468.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 09:37:36 | ||
图片预览

文档简介
第一单元 圆柱与圆锥(试题)--2023-2024-学年北师大版数学六年级下册
一、单选题
1.圆柱的体积公式推导过程,将圆柱切拼成一个近似的长方体后,( )。
A.表面积不变,体积不变 B.表面积变大,体积不变
C.表面积变大,体积变大 D.表面积变小,体积变小
2.把一个圆柱体木材加工成一个最大的圆锥,须削去圆柱体的( )
A. B. C.
3.如果正方体、圆柱、圆锥的底面积相等,高也相等。下面说法正确的是( )。
A.圆柱的体积比正方体的体积小 B.圆柱和正方体的表面积相同
C.圆柱的体积是圆锥的 D.圆锥的体积是正方体的
4.下面圆柱体(单位:厘米)的侧面积是( )
A.72.8平方厘米 B.62.8平方厘米
C.75.36平方厘米 D.125.6平方厘米
5.一个圆柱和一个圆锥的高相等,底面半径的比是2:3,圆柱和圆锥体积的比是( )
A.4:3 B.2:3 C.4:9
6.如图,两个大小相同的量杯中分别盛有250mL水。将等底等高的圆柱与圆锥零件分别放入这两个量杯中,这时甲杯的水面刻度如下图所示,则乙杯的水面刻度应是( )mL。
A.200 B.300 C.350 D.375
7.圆柱的高是圆锥高的一半,圆锥底面半径是圆柱底面半径的一半,圆锥的体积是圆柱体积的( )
A. B. C. D.
8.如图,A和B分别是长和宽的中点,阴影部分和整个长方形的面积比是( )
A.1:4 B.2:3 C.2:5 D.3:8
二、判断题
9.一个直角三角形沿一条边旋转一周,就会得到一个圆锥体。( )
10.两个圆柱的底面积相等,它们的体积也一定相等。( )
11.把一个圆柱削成一个最大的圆锥,圆锥的体积是削去部分的 。( )
12.圆柱的侧面展开图可能是平行四边形。( )
13.底面积为20平方厘米的圆柱的体积一定大于底面积为10平方厘米的圆柱的体积。( )
14.以三角形的一条边为轴旋转一周一定可以得到一个圆锥体。( )
15.把一个圆柱削成一个最大的圆锥,这个圆锥的体积与削去部分的体积是1:2。( )
16.一个圆锥的高缩小到原来的 ,底面半径扩大到原来的2倍,体积不变。( )
三、填空题
17.一个圆柱高5厘米,把它的侧面沿高展开后是一个长6.28厘米、宽5厘米的长方形,这个圆柱的底面直径是 厘米,侧面积是 平方厘米。
18.将体积为56.52立方分米的铁块熔铸成一个底面半径为6dm的圆锥体零件,圆锥的高是 分米。
19.一个圆柱,底面半径4厘米,高6厘米.它的底面周长是 厘米,底面积是 平方厘米,侧面积是 平方厘米,表面积是 平方厘米,体积是 立方厘米.把它削成一个最大的圆锥,圆锥的体积是 立方厘米.
20.一个圆柱的侧面积是314平方米,高是10米,它的底面周长是 米,底面直径是 米,表面积是 平方米。
21.将一根长2米的圆柱形木料沿着与横截面平行的方向截成3段,表面积比原来增加了156平方厘米,原来木料的体积是 立方厘米。
22.把一个棱长是6 dm的正方体木料削成一个最大的圆柱,圆柱的体积是 dm3 ;再将圆柱削成一个最大的圆锥,还要再削去 dm3。
23.一个圆柱与一个圆锥的底面积相等、体积也相等。若圆锥的高是2.4dm,则圆柱的高是 dm;若圆柱的高是2.4 dm,则圆锥的高是 dm。
四、计算题
24.下图是一个长方体的展开图,求这个长方体的表面积和体积。
25.计算下面图形的表面积和体积。(单位:dm)
五、作图题
26.一个圆柱的侧面积是25.12cm2,高是2cm,请在下面的方格纸上画出这个圆柱的两个底面。(每个小方格的面积表示1cm2)
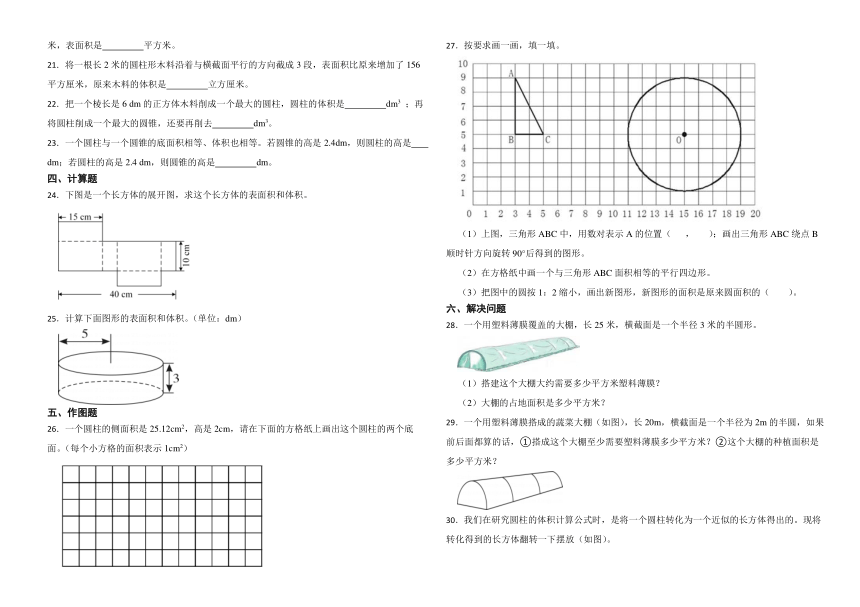
27.按要求画一画,填一填。
(1)上图,三角形ABC中,用数对表示A的位置( , );画出三角形ABC绕点B顺时针方向旋转90°后得到的图形。
(2)在方格纸中画一个与三角形ABC面积相等的平行四边形。
(3)把图中的圆按1:2缩小,画出新图形,新图形的面积是原来圆面积的( )。
六、解决问题
28.一个用塑料薄膜覆盖的大棚,长25米,横截面是一个半径3米的半圆形。
(1)搭建这个大棚大约需要多少平方米塑料薄膜?
(2)大棚的占地面积是多少平方米?
29.一个用塑料薄膜搭成的蔬菜大棚(如图),长20m,横截面是一个半径为2m的半圆,如果前后面都算的话,①搭成这个大棚至少需要塑料薄膜多少平方米?②这个大棚的种植面积是多少平方米?
30.我们在研究圆柱的体积计算公式时,是将一个圆柱转化为一个近似的长方体得出的。现将转化得到的长方体翻转一下摆放(如图)。
(1)观察上图,我们发现翻转后长方体的底面积等于圆柱 ,长方体的高等于圆柱的 ,因此圆柱的体积还可以这样计算: 。
(2)用你的发现解决问题:有一个圆柱,侧面积是120平方分米,底面半径是3分米,体积是多少立方分米?
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】D
4.【答案】C
5.【答案】A
6.【答案】B
7.【答案】C
8.【答案】D
9.【答案】错误
10.【答案】错误
11.【答案】正确
12.【答案】正确
13.【答案】错误
14.【答案】错误
15.【答案】正确
16.【答案】错误
17.【答案】2;31.4
18.【答案】1.5
19.【答案】25.12;50.24;150.72;251.2;301.44;100.48
20.【答案】31.4;10;471
21.【答案】7800
22.【答案】169.56;113.04
23.【答案】0.8;7.2
24.【答案】解:(40-15×2)÷2
=10÷2
=5(厘米)
15×10×2+15×5×2+10×5×2
=300+150+100
=550(平方厘米)
15×10×5=750(立方厘米)
答:表面积是550平方厘米,体积是750立方厘米。
25.【答案】解:表面积:3.14×52×2+3.14×5×2×3
=157+94.2
=251.2(dm2)
体积:3.14×52×3=235.5(dm3)
26.【答案】25.12÷2÷3.14
=12.56÷3.14
=4(厘米)
27.【答案】(1)解:用数对表示A的位置(3,9),如图:
(2)解:
(3)解:如图:
新图形的面积是原来圆面积的。
28.【答案】(1)解:3.14×3×2×25÷2+3.14×32
=3.14×75+3.14×9
=3.14×(75+9)
=3.14×84
=263.76(平方米)
答:搭建这个大棚大约需要263.76平方米塑料薄膜。
(2)解:2×3×25=150(平方米)
答:大棚的占地面积是150平方米。
29.【答案】解:①2×3.14×2×20÷2+3.14×22
=12.56×20÷2+3.14×4
=125.6+12.56
=138.16(平方米)
②20×2×2
=40×2
=80(平方米)
答:搭成这个大棚至少需要塑料薄膜138.16平方米,这个大棚的种植面积是80平方米。
30.【答案】(1)侧面积的一半;底面半径;圆柱的侧面积÷2×半径
(2)解:120÷2×3
=60×3
=180(立方分米)
答:体积是180立方分米。
一、单选题
1.圆柱的体积公式推导过程,将圆柱切拼成一个近似的长方体后,( )。
A.表面积不变,体积不变 B.表面积变大,体积不变
C.表面积变大,体积变大 D.表面积变小,体积变小
2.把一个圆柱体木材加工成一个最大的圆锥,须削去圆柱体的( )
A. B. C.
3.如果正方体、圆柱、圆锥的底面积相等,高也相等。下面说法正确的是( )。
A.圆柱的体积比正方体的体积小 B.圆柱和正方体的表面积相同
C.圆柱的体积是圆锥的 D.圆锥的体积是正方体的
4.下面圆柱体(单位:厘米)的侧面积是( )
A.72.8平方厘米 B.62.8平方厘米
C.75.36平方厘米 D.125.6平方厘米
5.一个圆柱和一个圆锥的高相等,底面半径的比是2:3,圆柱和圆锥体积的比是( )
A.4:3 B.2:3 C.4:9
6.如图,两个大小相同的量杯中分别盛有250mL水。将等底等高的圆柱与圆锥零件分别放入这两个量杯中,这时甲杯的水面刻度如下图所示,则乙杯的水面刻度应是( )mL。
A.200 B.300 C.350 D.375
7.圆柱的高是圆锥高的一半,圆锥底面半径是圆柱底面半径的一半,圆锥的体积是圆柱体积的( )
A. B. C. D.
8.如图,A和B分别是长和宽的中点,阴影部分和整个长方形的面积比是( )
A.1:4 B.2:3 C.2:5 D.3:8
二、判断题
9.一个直角三角形沿一条边旋转一周,就会得到一个圆锥体。( )
10.两个圆柱的底面积相等,它们的体积也一定相等。( )
11.把一个圆柱削成一个最大的圆锥,圆锥的体积是削去部分的 。( )
12.圆柱的侧面展开图可能是平行四边形。( )
13.底面积为20平方厘米的圆柱的体积一定大于底面积为10平方厘米的圆柱的体积。( )
14.以三角形的一条边为轴旋转一周一定可以得到一个圆锥体。( )
15.把一个圆柱削成一个最大的圆锥,这个圆锥的体积与削去部分的体积是1:2。( )
16.一个圆锥的高缩小到原来的 ,底面半径扩大到原来的2倍,体积不变。( )
三、填空题
17.一个圆柱高5厘米,把它的侧面沿高展开后是一个长6.28厘米、宽5厘米的长方形,这个圆柱的底面直径是 厘米,侧面积是 平方厘米。
18.将体积为56.52立方分米的铁块熔铸成一个底面半径为6dm的圆锥体零件,圆锥的高是 分米。
19.一个圆柱,底面半径4厘米,高6厘米.它的底面周长是 厘米,底面积是 平方厘米,侧面积是 平方厘米,表面积是 平方厘米,体积是 立方厘米.把它削成一个最大的圆锥,圆锥的体积是 立方厘米.
20.一个圆柱的侧面积是314平方米,高是10米,它的底面周长是 米,底面直径是 米,表面积是 平方米。
21.将一根长2米的圆柱形木料沿着与横截面平行的方向截成3段,表面积比原来增加了156平方厘米,原来木料的体积是 立方厘米。
22.把一个棱长是6 dm的正方体木料削成一个最大的圆柱,圆柱的体积是 dm3 ;再将圆柱削成一个最大的圆锥,还要再削去 dm3。
23.一个圆柱与一个圆锥的底面积相等、体积也相等。若圆锥的高是2.4dm,则圆柱的高是 dm;若圆柱的高是2.4 dm,则圆锥的高是 dm。
四、计算题
24.下图是一个长方体的展开图,求这个长方体的表面积和体积。
25.计算下面图形的表面积和体积。(单位:dm)
五、作图题
26.一个圆柱的侧面积是25.12cm2,高是2cm,请在下面的方格纸上画出这个圆柱的两个底面。(每个小方格的面积表示1cm2)
27.按要求画一画,填一填。
(1)上图,三角形ABC中,用数对表示A的位置( , );画出三角形ABC绕点B顺时针方向旋转90°后得到的图形。
(2)在方格纸中画一个与三角形ABC面积相等的平行四边形。
(3)把图中的圆按1:2缩小,画出新图形,新图形的面积是原来圆面积的( )。
六、解决问题
28.一个用塑料薄膜覆盖的大棚,长25米,横截面是一个半径3米的半圆形。
(1)搭建这个大棚大约需要多少平方米塑料薄膜?
(2)大棚的占地面积是多少平方米?
29.一个用塑料薄膜搭成的蔬菜大棚(如图),长20m,横截面是一个半径为2m的半圆,如果前后面都算的话,①搭成这个大棚至少需要塑料薄膜多少平方米?②这个大棚的种植面积是多少平方米?
30.我们在研究圆柱的体积计算公式时,是将一个圆柱转化为一个近似的长方体得出的。现将转化得到的长方体翻转一下摆放(如图)。
(1)观察上图,我们发现翻转后长方体的底面积等于圆柱 ,长方体的高等于圆柱的 ,因此圆柱的体积还可以这样计算: 。
(2)用你的发现解决问题:有一个圆柱,侧面积是120平方分米,底面半径是3分米,体积是多少立方分米?
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】D
4.【答案】C
5.【答案】A
6.【答案】B
7.【答案】C
8.【答案】D
9.【答案】错误
10.【答案】错误
11.【答案】正确
12.【答案】正确
13.【答案】错误
14.【答案】错误
15.【答案】正确
16.【答案】错误
17.【答案】2;31.4
18.【答案】1.5
19.【答案】25.12;50.24;150.72;251.2;301.44;100.48
20.【答案】31.4;10;471
21.【答案】7800
22.【答案】169.56;113.04
23.【答案】0.8;7.2
24.【答案】解:(40-15×2)÷2
=10÷2
=5(厘米)
15×10×2+15×5×2+10×5×2
=300+150+100
=550(平方厘米)
15×10×5=750(立方厘米)
答:表面积是550平方厘米,体积是750立方厘米。
25.【答案】解:表面积:3.14×52×2+3.14×5×2×3
=157+94.2
=251.2(dm2)
体积:3.14×52×3=235.5(dm3)
26.【答案】25.12÷2÷3.14
=12.56÷3.14
=4(厘米)
27.【答案】(1)解:用数对表示A的位置(3,9),如图:
(2)解:
(3)解:如图:
新图形的面积是原来圆面积的。
28.【答案】(1)解:3.14×3×2×25÷2+3.14×32
=3.14×75+3.14×9
=3.14×(75+9)
=3.14×84
=263.76(平方米)
答:搭建这个大棚大约需要263.76平方米塑料薄膜。
(2)解:2×3×25=150(平方米)
答:大棚的占地面积是150平方米。
29.【答案】解:①2×3.14×2×20÷2+3.14×22
=12.56×20÷2+3.14×4
=125.6+12.56
=138.16(平方米)
②20×2×2
=40×2
=80(平方米)
答:搭成这个大棚至少需要塑料薄膜138.16平方米,这个大棚的种植面积是80平方米。
30.【答案】(1)侧面积的一半;底面半径;圆柱的侧面积÷2×半径
(2)解:120÷2×3
=60×3
=180(立方分米)
答:体积是180立方分米。
