圆柱与圆锥应用题易错汇编-数学六年级下册北师大版(含解析)
文档属性
| 名称 | 圆柱与圆锥应用题易错汇编-数学六年级下册北师大版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 493.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 11:05:50 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
圆柱与圆锥应用题易错汇编-数学六年级下册北师大版
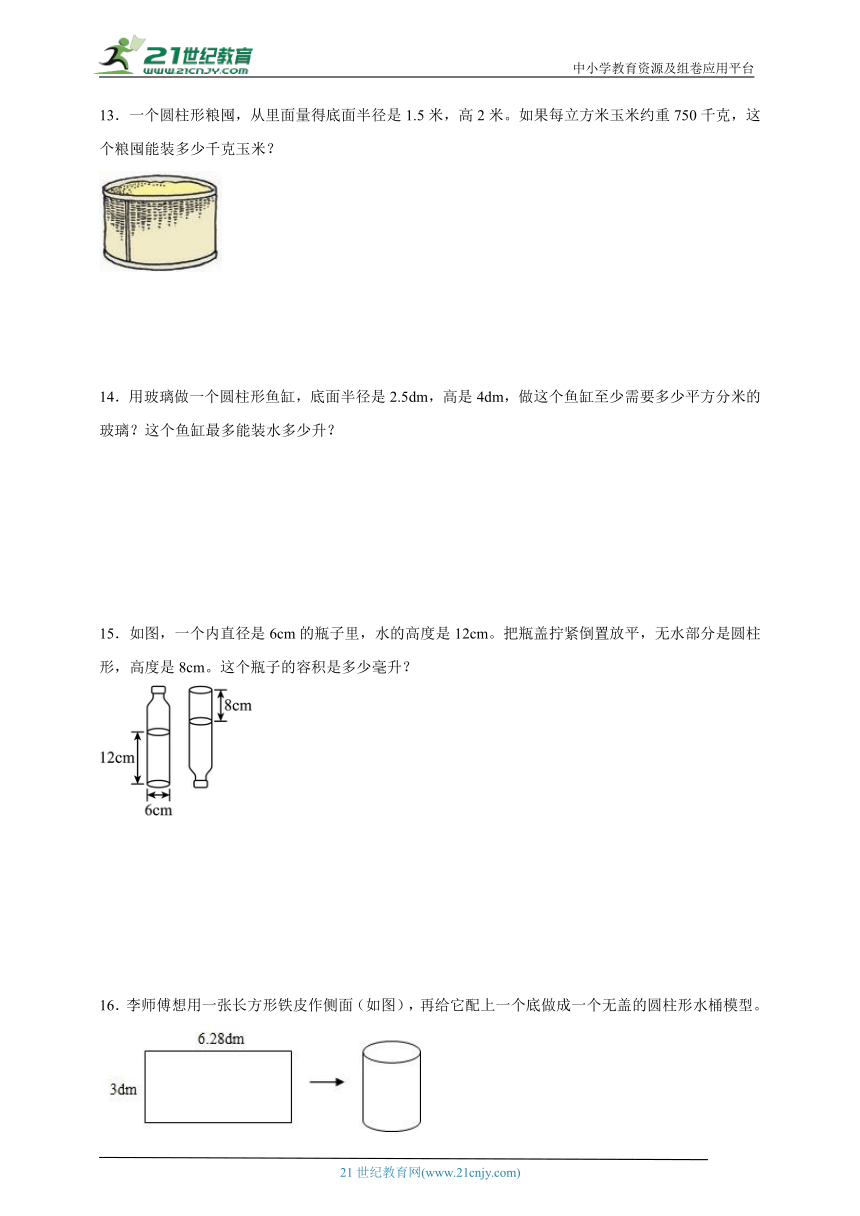
1.把一块长方体钢坯铸造成一个直径为12分米的圆锥形零件,求圆锥形零件的高。
2.一个圆锥形麦子堆的底面周长是12.56米,高是1.8米。现在把这些麦子全部装入一个底面周长是6.28米的圆柱形粮囤里,可以装多高?
3.有一个圆锥形的煤炭堆,底面周长是31.4米,高是2米。一辆车一次可以运5立方米的煤炭,用这辆车大约几次可以运完?(π≈3.14)
4.一个蒙古包总高度为3.2米,它的圆柱形部分底面周长为31.4米,圆锥形部分高为1.2米。
(1)这个蒙古包占地多少平方米?
(2)不计蒙古包壁的厚度,这个蒙古包的容积有多大?
5.一个圆锥形沙堆,底面积是56.52平方米,高是3米。用这堆沙在10米宽的公路上铺3厘米厚的路面,能铺多少米?
6.“神舟飞船”是中国自行研制的载人航天飞船。
(1)2023年5月30日上午9时31分“神舟十六号”点火发射,5月30日下午6时53分与“神舟十五号”在太空中成功会师,“神舟十六号”从点火发射到与“神舟十五号”成功会师用了多长时间?
(2实验小学同学做了一个运载火箭的模型,如下图,圆柱部分的体积是圆锥部分的多少倍?
7.我国古代的数学名著《九章算术》中的“商功”,记载着这样一种求圆锥体积的方法:“下周自乘,以高乘之,三十六而一。”意思就是用底面周长的平方乘高,再除以36,可以得到这个圆锥的体积。(本题中的值取3)
(1)利用上述方法求上图所示圆锥的体积。(单位:厘米)
(2)你能用所学的数学知识解释这里面的道理吗?
8.一个底面半径为10厘米,高为15厘米的圆柱形容器,里面装有高12厘米的水,将一个底面半径为5厘米,高9厘米的圆锥完全浸没在水中,且没有溢出,现在水面高度是多少厘米?
9.下面每个小正方形的边长为1厘米,请按要求完成下列各题。
(1)画出三角形绕点顺时针旋转90°的图形。
(2)画出三角形向右平移4格后的图形。
(3)画出三角形斜边上的高。
(4)以三角形的边为轴旋转一周形成的图形是( ),它的高是( )厘米,体积是( )立方厘米。
10.把底面半径是4厘米,高是5厘米的圆柱形钢件熔铸成一个底面积是78.5平方厘米的圆锥形零件。这件圆锥形零件的高是多少厘米?
11.一个圆柱形蓄水池,直径10m,深2m。
(1)这个蓄水池的占地面积是多少?
(2)在池的一周及池底抹上水泥,抹水泥的面积是多少?
(3)这个蓄水池最多能装多少水?
12.有甲、乙两只圆柱形玻璃杯,其内直径依次是18厘米、12厘米,杯中盛有适量的水.甲杯中沉没着一铁块,当取出此铁块后,甲杯中的水位下降了2厘米;然后将铁块沉没于乙杯,且乙杯中的水未外溢.问:这时乙杯中的水位上升了多少厘米?
13.一个圆柱形粮囤,从里面量得底面半径是1.5米,高2米。如果每立方米玉米约重750千克,这个粮囤能装多少千克玉米?
14.用玻璃做一个圆柱形鱼缸,底面半径是2.5dm,高是4dm,做这个鱼缸至少需要多少平方分米的玻璃?这个鱼缸最多能装水多少升?
15.如图,一个内直径是6cm的瓶子里,水的高度是12cm。把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是8cm。这个瓶子的容积是多少毫升?
16.李师傅想用一张长方形铁皮作侧面(如图),再给它配上一个底做成一个无盖的圆柱形水桶模型。
(1)下面有4张铁皮(单位:),从节约材料的角度出发,李师傅会选择( )作这个水桶的底。水桶的底面直径是( ),水桶高( )。
A.B.C.D.
(2)这个水桶的容积是多少?(铁皮厚度忽略不计)
(3)盛满水后,水与桶接触的面一共有多少平方分米?
17.如图,左边是一个装满了果汁的饮料盒,右边是一个茶杯,茶杯的底面直径是10厘米,高是8厘米.如果把饮料盒内的果汁全部倒入右边的茶杯里,能倒满几杯?
18.小雪家有一个长方体玻璃鱼缸,长1.5m,宽0.6m,深0.4m.爸爸用底面积是3cm2的圆柱形排水管给鱼缸排水.如果水流速度按每分40m计算,排完一满缸水需要多少分?
19.有两个高相等的圆柱,底面半径的比是2:5,第一个圆柱的体积是360立方厘米,那么第二个圆柱的体积是多少立方厘米?
20.用下面的铁皮正好能做成一个圆柱,且没有剩余。那么,这些铁皮做成的圆柱的表面积是多少?体积是多少?
21.一种圆柱形茶叶罐,底面直径是10厘米,高是12厘米,将4个这样的茶叶罐按如图所示的方式紧密地放入纸盒中。这个纸盒中空隙部分的体积是多少?
参考答案:
1.8分米
【分析】根据体积的意义,把长方体钢坯铸造成圆锥体后体积不变,根据长方体体积公式:V=abh,圆锥体积公式:V=Sh,那么h=V÷÷S,同时底面积公式为:S=r2,用直径的长度除以2可得半径的长度,由此将数据代入可求出圆锥的高。
【详解】由分析可得:
12.56×4×6÷÷[3.14×(12÷2)2]
=12.56×4×6÷÷[3.14×62]
=12.56×4×6÷÷[3.14×36]
=12.56×4×6÷÷113.04
=50.24×6×3÷113.04
=301.44×3÷113.04
=904.32÷113.04
=8(分米)
答:圆锥的高是8分米。
【点睛】本题考查了长方体体积公式,圆锥体积公式,底面积公式的灵活运用,解题的关键是牢记公式。
2.2.4米
【分析】根据圆的半径=周长÷圆周率÷2,先求出底面半径,再根据圆锥体积=底面积×高÷3,求出麦子体积,麦子体积÷圆柱形粮囤底面积=高,据此列式解答。
【详解】12.56÷3.14÷2=2(米)
3.14×22×1.8÷3
=3.14×4×1.8÷3
=7.536(立方米)
6.28÷3.14÷2=1(米)
7.536÷(3.14×12)
=7.536÷(3.14×1)
=7.536÷3.14
=2.4(米)
答:可以装2.4米高。
【点睛】关键是掌握并灵活运用圆柱和圆锥体积公式。
3.11次
【分析】根据圆的周长公式:周长=π×半径×2;半径=周长÷π÷2,代入数据,求出圆锥形的煤炭堆的底面半径,再根据圆锥的体积公式:体积=底面积×高×,代入数据,求出圆锥形煤炭堆的体积,再除以5,即可解答,由于最后就算剩下一点,也需要一辆车运走,所以结果用进一法取值。
【详解】31.4÷3.14÷2
=10÷2
=5(米)
3.14×52×2×÷5
=3.14×25×2×÷5
=78.5×2×÷5
=157×÷5
≈52.3÷5
≈11(次)
答:用这辆车大约11次可以运完
【点睛】本题考查圆的周长公式、圆锥的体积公式的应用以及结果用“进一法”解答。
4.(1)78.5平方米;(2)188.4立方米
【分析】(1)蒙古包的底面是一个圆,占地面积指的是蒙古包的底面积也就是圆的面积,利用圆柱的底面周长求出圆的半径,再代入到圆的面积公式即可;
(2)蒙古包的容积分为圆柱部分和圆锥部分,将数据分别代入圆柱和圆锥的体积公式计算即可,注意圆柱的高=3.2-1.2=2米。
【详解】(1)半径:
31.4÷3.14÷2
=10÷2
=5(米)
3.14×5
=3.14×25
=78.5(平方米)
答:这个蒙古包占地78.5平方米。
(2)78.5×(3.2-1.2)+78.5×1.2÷3
=78.5×2+94.2÷3
=157+31.4
=188.4(立方米)
答:不计蒙古包壁的厚度,这个蒙古包的容积有188.4立方米。
【点睛】此题主要考查圆柱和圆锥的容积公式,利用底面周长求出圆的半径是解题的关键。
5.188.4米
【分析】3厘米=0.03米,根据圆锥的体积公式:V=Sh,用×56.52×3即可求出沙堆的体积,再根据长方体的体积=长×宽×高,用长方体的体积÷10÷0.03即可求出能铺的米数。
【详解】这个圆锥形沙堆的体积是:×56.52×3=56.52(立方米)
3厘米=0.03米
用这堆沙铺路能铺:56.52÷10÷0.03=188.4(米)
答:用这堆沙铺路,能铺188.4米。
【点睛】本题主要考查了圆锥的体积公式、长方体的体积公式的灵活应用,要熟练掌握公式。
6.(1)9时22分
(2)6
【分析】(1)将12时计时法转化成24时计时法,根据终点时间-起点时间=经过时间,列式解答即可;
(2)圆柱体积=底面积×高,圆锥体积=底面积×高÷3,圆柱体积÷圆锥体积即可。
【详解】(1)上午9时31分→9时31分
下午6时53分→18时53分
18时53分-9时31分=9时22分
答:“神舟十六号”从点火发射到与“神舟十五号”成功会师用了9时22分。
(2)2÷2=1(厘米)
3.14×12×6
=3.14×1×6
=18.84(立方厘米)
3.14×12×3÷3
=3.14×1×3÷3
=3.14(立方厘米)
18.84÷3.14=6
答:圆柱部分的体积是圆锥部分的6倍。
【点睛】关键是会计算经过时间,掌握并灵活运用圆柱和圆锥体积公式。
7.(1)24立方厘米
(2)见详解
【分析】(1)根据圆锥的体积=底面周长2×高÷36,列式计算即可。
(2)圆锥的体积=底面积×高=,圆的周长=2πr,因此将题干描述的圆锥的体积=底面周长2×高÷36,进行转化,得到即可。
【详解】(1)(2×3×2)2×6÷36
=122×6÷36
=144×6÷36
=24(立方厘米)
答:圆锥的体积是24立方厘米。
(2)
将π=3代入其中一个π
圆锥的体积公式:,根据题目意思可得圆锥的体积为,当取3,可以将化简为,因此“商功”中求圆锥体积的方法也可以求出圆锥体积。
【点睛】关键是读懂题意,掌握并灵活运用圆锥体积公式。
8.12.75厘米
【分析】根据圆锥体积=底面积×高÷3,求出圆锥的体积,圆锥的体积÷圆柱形容器底面积=水面上升的高度,水面上升的高度+原来水的高度=现在水面高度,据此列式解答。
【详解】3.14×52×9÷3÷(3.14×102)+12
=3.14×25×9÷3÷(3.14×100)+12
=235.5÷314+12
=0.75+12
=12.75(厘米)
答:现在水面高度是12.75厘米。
【点睛】关键是掌握并灵活运用圆柱和圆锥体积公式。
9.(1)、(2)、(3)见详解
(4)圆锥;3;12.56
【分析】(1)根据旋转的特征,三角形ABC绕点B顺时针旋转90°,点B的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(2)根据平移的特征,把三角形ABC的各顶点分别向右平移4格,依次连接即可得到向右平移4格后的图形。
(3)过B点画一条线段垂直于斜边AC,即为三角形斜边上的高。
(4)以三角形的边为轴旋转一周形成的图形是是圆锥,它的高是直角边AB的长,底面半径是2厘米,圆锥的体积=底面积×高×,将数据代入即可求得圆锥的体积。
【详解】(1)、(2)、(3)画图如下:
(4)3.14×2×2×3×
=3.14×4
=12.56(立方厘米)
以三角形的边为轴旋转一周形成的图形是(圆锥),它的高是(3)厘米,体积是(12.56)立方厘米。
【点睛】本题主要考了平面图形角旋转、平移及三角形高的画法及圆锥体积公式的灵活运用。
10.9.6厘米
【分析】根据圆柱的体积公式:V=πr2h,用3.14×42×5即可求出圆柱形钢件的体积,熔铸成一个圆锥形零件,体积不变,根据圆锥的体积公式:V=Sh,用零件的体积×3÷78.5即可求出零件的高度。据此解答。
【详解】3.14×42×5
=3.14×16×5
=251.2(立方厘米)
251.2×3÷78.5=9.6(厘米)
答:这件圆锥形零件的高是9.6厘米。
【点睛】本题主要考查了圆柱的体积公式和圆锥的体积公式的灵活应用,要熟练掌握公式。
11.(1)78.5m2
(2)141.3m2
(3)157000L
【分析】(1)水池的占地面积,就是这个圆柱形水池的底面积,由此利用底面直径求出这个圆柱的底面半径再代入圆的面积公式计算即可解答;
(2)抹水泥的面积就是这个圆柱水池的底面积加侧面积,利用圆柱的侧面积=底面周长×高计算出圆柱的侧面积,再加上底面积即可解答;
(3)要求这个水池能装多少水,就是求这个圆柱形水池的容积,利用圆柱的容积公式即可解答。
【详解】(1)10÷2=5(m)
3.14×52=78.5(m2)
答:水池的占地面积是78.5m2。
(2)3.14×10×2+78.5
=62.8+78.5
=141.3(m2)
答:抹水泥的部分是141.3m2。
(3)3.14×52×2
=3.14×25×2
=157(m3)
=157000(L)
答:这个水池能装157000L的水。
【点睛】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决。
12.4.5厘米
【分析】由题意可知:当甲杯中取出铁块后,水面下降部分水的体积就等于铁块的体积,即底面直径18厘米、高是2厘米的圆柱的体积;然后再除以乙杯的底面积,就是水位上升的高度.
【详解】3.14×(18÷2)2×2÷3.14÷(12÷2)2=4.5(厘米)
答:这时乙杯中的水位上升了4.5厘米.
13.10597.5千克
【分析】根据圆柱的体积公式,先列式计算出粮囤的体积,再将体积乘每立方米玉米的重量750千克,求出这个粮囤能装多少千克玉米。
【详解】3.14×1.52×2×750
=14.13×750
=10597.5(千克)
答:这个粮囤能装10597.5千克玉米。
【点睛】本题考查了圆柱的体积,圆柱的体积=底面积×高。
14.82.425dm2 78.5L
【详解】3.14×2.5×2×4+3.14×2.52=82.425(dm2)
3.14×2.52×4=78.5(dm3)=78.5(L)
答:做这个鱼缸至少需要82.425 dm2的玻璃,这个鱼缸最多能装水78.5 L.
15.565.2毫升
【分析】瓶子的两种放法,无水部分的容积是不变的,将右图中无水部分的圆柱移到左图,替换不规则的无水部分,则求瓶子的容积转化成求底面直径6cm,高(12+8)cm的圆柱形瓶子的容积,根据圆柱的体积公式V=πr2h,代入数据计算,最后根据进率“1立方厘米=1毫升”换算单位。
【详解】6÷2=3(厘米)
3.14×32×(12+8)
=3.14×9×20
=3.14×180
=565.2(立方厘米)
565.2立方厘米=565.2毫升
答:这个瓶子的容积是565.2毫升。
【点睛】明确瓶子倒置后无水部分的容积和正放时无水部分的容积相等是解题的关键。
16.(1)B;2;3
(2)9.42立方分米
(3)21.98平方分米
【分析】(1)因为用长方形铁皮作为圆柱的侧面,所以在此题中长方形的宽为圆柱的高,长方形的长为圆柱的底面周长,底面周长公式为:C=πd,求出直径,再将出4张铁皮较短的边与底面直径比较,从而决定选择哪一张。
(2)圆柱的体积公式为:V=Sh=πrh。
(3)因为此圆柱形水桶是无盖的,所以水与桶接触的面也就是一个底面和圆柱的侧面。
【详解】(1)圆柱的底面直径为:6.28÷3.14=2(dm),B中的边长恰好等于圆的直径,所以B铁皮作水桶的底最合适。水桶的底面直径是2,水桶高3。
(2)3.14×(2÷2)×3
=3.14×3
=9.42(立方分米)
答:这个水桶的容积为9.42立方分米。
(3)3.14×(2÷2)+6.28×3
=3.14+18.84
=21.98(平方分米)
答:盛满水后,水与桶接触的面一共有21.98平方分米。
【点睛】掌握圆柱的体积公式和侧面积公式是解决本题的关键。
17.5杯
【分析】先分别求出饮料盒里果汁的体积和茶杯的容积,再用除法计算.
【详解】30×20×6=3600(立方厘米)
3.14×(10÷2)2×8=628(立方厘米)
3600÷628≈5(杯)
答:能倒满5杯.
18.30分
【详解】1.5×0.6×0.4=0.36(m3) 0.36m3=360000cm3 40m=4000cm 360000÷(3×4000)=30(分)
19.2250
【详解】试题分析:因为两个圆柱的高一定,体积与底面积成正比,也与半径的平方成正比,所以两个圆柱的体积比为:22:52=4:25,那么360是第二个圆柱的体积的,根据分数除法的意义,那么第二个圆柱的体积是:360=2250(立方厘米),据此解答.
解:两个圆柱的体积比为:22:52=4:25,
360=2250(立方厘米);
答:第二个圆柱的体积是2250立方厘米.
点评:本题考查了比的灵活应用,关键是求出两个圆柱的体积的比,继而转化为两个量的分率关系,然后根据分数除法的意义解答即可.
20.31.4dm2;12.56dm3
【分析】由图可知,圆柱的底面直径为(4÷2)dm,计算出圆柱的底面半径,圆柱的高为4dm,利用和求出圆柱的表面积和体积,据此解答。
【详解】半径:4÷2÷2
=2÷2
=1(dm)
表面积:3.14×(4÷2)×4+2×3.14×12
=3.14×2×4+2×3.14×12
=6.28×4+6.28
=25.12+6.28
=31.4(dm2)
体积:3.14×12×4
=3.14×4
=12.56(dm3)
答:圆柱的表面积是31.4dm2;体积是12.56dm3。
【点睛】本题主要考查圆柱表面积和体积的应用,熟记公式是解答题目的关键。
21.1032立方厘米
【详解】(10×2)×(10×2)×12﹣3.14××12×4
=20×20×12﹣3.14×25×12×4
=4800﹣3768
=1032(立方厘米)
答:这个纸盒中空隙部分的体积是1032立方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
圆柱与圆锥应用题易错汇编-数学六年级下册北师大版
1.把一块长方体钢坯铸造成一个直径为12分米的圆锥形零件,求圆锥形零件的高。
2.一个圆锥形麦子堆的底面周长是12.56米,高是1.8米。现在把这些麦子全部装入一个底面周长是6.28米的圆柱形粮囤里,可以装多高?
3.有一个圆锥形的煤炭堆,底面周长是31.4米,高是2米。一辆车一次可以运5立方米的煤炭,用这辆车大约几次可以运完?(π≈3.14)
4.一个蒙古包总高度为3.2米,它的圆柱形部分底面周长为31.4米,圆锥形部分高为1.2米。
(1)这个蒙古包占地多少平方米?
(2)不计蒙古包壁的厚度,这个蒙古包的容积有多大?
5.一个圆锥形沙堆,底面积是56.52平方米,高是3米。用这堆沙在10米宽的公路上铺3厘米厚的路面,能铺多少米?
6.“神舟飞船”是中国自行研制的载人航天飞船。
(1)2023年5月30日上午9时31分“神舟十六号”点火发射,5月30日下午6时53分与“神舟十五号”在太空中成功会师,“神舟十六号”从点火发射到与“神舟十五号”成功会师用了多长时间?
(2实验小学同学做了一个运载火箭的模型,如下图,圆柱部分的体积是圆锥部分的多少倍?
7.我国古代的数学名著《九章算术》中的“商功”,记载着这样一种求圆锥体积的方法:“下周自乘,以高乘之,三十六而一。”意思就是用底面周长的平方乘高,再除以36,可以得到这个圆锥的体积。(本题中的值取3)
(1)利用上述方法求上图所示圆锥的体积。(单位:厘米)
(2)你能用所学的数学知识解释这里面的道理吗?
8.一个底面半径为10厘米,高为15厘米的圆柱形容器,里面装有高12厘米的水,将一个底面半径为5厘米,高9厘米的圆锥完全浸没在水中,且没有溢出,现在水面高度是多少厘米?
9.下面每个小正方形的边长为1厘米,请按要求完成下列各题。
(1)画出三角形绕点顺时针旋转90°的图形。
(2)画出三角形向右平移4格后的图形。
(3)画出三角形斜边上的高。
(4)以三角形的边为轴旋转一周形成的图形是( ),它的高是( )厘米,体积是( )立方厘米。
10.把底面半径是4厘米,高是5厘米的圆柱形钢件熔铸成一个底面积是78.5平方厘米的圆锥形零件。这件圆锥形零件的高是多少厘米?
11.一个圆柱形蓄水池,直径10m,深2m。
(1)这个蓄水池的占地面积是多少?
(2)在池的一周及池底抹上水泥,抹水泥的面积是多少?
(3)这个蓄水池最多能装多少水?
12.有甲、乙两只圆柱形玻璃杯,其内直径依次是18厘米、12厘米,杯中盛有适量的水.甲杯中沉没着一铁块,当取出此铁块后,甲杯中的水位下降了2厘米;然后将铁块沉没于乙杯,且乙杯中的水未外溢.问:这时乙杯中的水位上升了多少厘米?
13.一个圆柱形粮囤,从里面量得底面半径是1.5米,高2米。如果每立方米玉米约重750千克,这个粮囤能装多少千克玉米?
14.用玻璃做一个圆柱形鱼缸,底面半径是2.5dm,高是4dm,做这个鱼缸至少需要多少平方分米的玻璃?这个鱼缸最多能装水多少升?
15.如图,一个内直径是6cm的瓶子里,水的高度是12cm。把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是8cm。这个瓶子的容积是多少毫升?
16.李师傅想用一张长方形铁皮作侧面(如图),再给它配上一个底做成一个无盖的圆柱形水桶模型。
(1)下面有4张铁皮(单位:),从节约材料的角度出发,李师傅会选择( )作这个水桶的底。水桶的底面直径是( ),水桶高( )。
A.B.C.D.
(2)这个水桶的容积是多少?(铁皮厚度忽略不计)
(3)盛满水后,水与桶接触的面一共有多少平方分米?
17.如图,左边是一个装满了果汁的饮料盒,右边是一个茶杯,茶杯的底面直径是10厘米,高是8厘米.如果把饮料盒内的果汁全部倒入右边的茶杯里,能倒满几杯?
18.小雪家有一个长方体玻璃鱼缸,长1.5m,宽0.6m,深0.4m.爸爸用底面积是3cm2的圆柱形排水管给鱼缸排水.如果水流速度按每分40m计算,排完一满缸水需要多少分?
19.有两个高相等的圆柱,底面半径的比是2:5,第一个圆柱的体积是360立方厘米,那么第二个圆柱的体积是多少立方厘米?
20.用下面的铁皮正好能做成一个圆柱,且没有剩余。那么,这些铁皮做成的圆柱的表面积是多少?体积是多少?
21.一种圆柱形茶叶罐,底面直径是10厘米,高是12厘米,将4个这样的茶叶罐按如图所示的方式紧密地放入纸盒中。这个纸盒中空隙部分的体积是多少?
参考答案:
1.8分米
【分析】根据体积的意义,把长方体钢坯铸造成圆锥体后体积不变,根据长方体体积公式:V=abh,圆锥体积公式:V=Sh,那么h=V÷÷S,同时底面积公式为:S=r2,用直径的长度除以2可得半径的长度,由此将数据代入可求出圆锥的高。
【详解】由分析可得:
12.56×4×6÷÷[3.14×(12÷2)2]
=12.56×4×6÷÷[3.14×62]
=12.56×4×6÷÷[3.14×36]
=12.56×4×6÷÷113.04
=50.24×6×3÷113.04
=301.44×3÷113.04
=904.32÷113.04
=8(分米)
答:圆锥的高是8分米。
【点睛】本题考查了长方体体积公式,圆锥体积公式,底面积公式的灵活运用,解题的关键是牢记公式。
2.2.4米
【分析】根据圆的半径=周长÷圆周率÷2,先求出底面半径,再根据圆锥体积=底面积×高÷3,求出麦子体积,麦子体积÷圆柱形粮囤底面积=高,据此列式解答。
【详解】12.56÷3.14÷2=2(米)
3.14×22×1.8÷3
=3.14×4×1.8÷3
=7.536(立方米)
6.28÷3.14÷2=1(米)
7.536÷(3.14×12)
=7.536÷(3.14×1)
=7.536÷3.14
=2.4(米)
答:可以装2.4米高。
【点睛】关键是掌握并灵活运用圆柱和圆锥体积公式。
3.11次
【分析】根据圆的周长公式:周长=π×半径×2;半径=周长÷π÷2,代入数据,求出圆锥形的煤炭堆的底面半径,再根据圆锥的体积公式:体积=底面积×高×,代入数据,求出圆锥形煤炭堆的体积,再除以5,即可解答,由于最后就算剩下一点,也需要一辆车运走,所以结果用进一法取值。
【详解】31.4÷3.14÷2
=10÷2
=5(米)
3.14×52×2×÷5
=3.14×25×2×÷5
=78.5×2×÷5
=157×÷5
≈52.3÷5
≈11(次)
答:用这辆车大约11次可以运完
【点睛】本题考查圆的周长公式、圆锥的体积公式的应用以及结果用“进一法”解答。
4.(1)78.5平方米;(2)188.4立方米
【分析】(1)蒙古包的底面是一个圆,占地面积指的是蒙古包的底面积也就是圆的面积,利用圆柱的底面周长求出圆的半径,再代入到圆的面积公式即可;
(2)蒙古包的容积分为圆柱部分和圆锥部分,将数据分别代入圆柱和圆锥的体积公式计算即可,注意圆柱的高=3.2-1.2=2米。
【详解】(1)半径:
31.4÷3.14÷2
=10÷2
=5(米)
3.14×5
=3.14×25
=78.5(平方米)
答:这个蒙古包占地78.5平方米。
(2)78.5×(3.2-1.2)+78.5×1.2÷3
=78.5×2+94.2÷3
=157+31.4
=188.4(立方米)
答:不计蒙古包壁的厚度,这个蒙古包的容积有188.4立方米。
【点睛】此题主要考查圆柱和圆锥的容积公式,利用底面周长求出圆的半径是解题的关键。
5.188.4米
【分析】3厘米=0.03米,根据圆锥的体积公式:V=Sh,用×56.52×3即可求出沙堆的体积,再根据长方体的体积=长×宽×高,用长方体的体积÷10÷0.03即可求出能铺的米数。
【详解】这个圆锥形沙堆的体积是:×56.52×3=56.52(立方米)
3厘米=0.03米
用这堆沙铺路能铺:56.52÷10÷0.03=188.4(米)
答:用这堆沙铺路,能铺188.4米。
【点睛】本题主要考查了圆锥的体积公式、长方体的体积公式的灵活应用,要熟练掌握公式。
6.(1)9时22分
(2)6
【分析】(1)将12时计时法转化成24时计时法,根据终点时间-起点时间=经过时间,列式解答即可;
(2)圆柱体积=底面积×高,圆锥体积=底面积×高÷3,圆柱体积÷圆锥体积即可。
【详解】(1)上午9时31分→9时31分
下午6时53分→18时53分
18时53分-9时31分=9时22分
答:“神舟十六号”从点火发射到与“神舟十五号”成功会师用了9时22分。
(2)2÷2=1(厘米)
3.14×12×6
=3.14×1×6
=18.84(立方厘米)
3.14×12×3÷3
=3.14×1×3÷3
=3.14(立方厘米)
18.84÷3.14=6
答:圆柱部分的体积是圆锥部分的6倍。
【点睛】关键是会计算经过时间,掌握并灵活运用圆柱和圆锥体积公式。
7.(1)24立方厘米
(2)见详解
【分析】(1)根据圆锥的体积=底面周长2×高÷36,列式计算即可。
(2)圆锥的体积=底面积×高=,圆的周长=2πr,因此将题干描述的圆锥的体积=底面周长2×高÷36,进行转化,得到即可。
【详解】(1)(2×3×2)2×6÷36
=122×6÷36
=144×6÷36
=24(立方厘米)
答:圆锥的体积是24立方厘米。
(2)
将π=3代入其中一个π
圆锥的体积公式:,根据题目意思可得圆锥的体积为,当取3,可以将化简为,因此“商功”中求圆锥体积的方法也可以求出圆锥体积。
【点睛】关键是读懂题意,掌握并灵活运用圆锥体积公式。
8.12.75厘米
【分析】根据圆锥体积=底面积×高÷3,求出圆锥的体积,圆锥的体积÷圆柱形容器底面积=水面上升的高度,水面上升的高度+原来水的高度=现在水面高度,据此列式解答。
【详解】3.14×52×9÷3÷(3.14×102)+12
=3.14×25×9÷3÷(3.14×100)+12
=235.5÷314+12
=0.75+12
=12.75(厘米)
答:现在水面高度是12.75厘米。
【点睛】关键是掌握并灵活运用圆柱和圆锥体积公式。
9.(1)、(2)、(3)见详解
(4)圆锥;3;12.56
【分析】(1)根据旋转的特征,三角形ABC绕点B顺时针旋转90°,点B的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(2)根据平移的特征,把三角形ABC的各顶点分别向右平移4格,依次连接即可得到向右平移4格后的图形。
(3)过B点画一条线段垂直于斜边AC,即为三角形斜边上的高。
(4)以三角形的边为轴旋转一周形成的图形是是圆锥,它的高是直角边AB的长,底面半径是2厘米,圆锥的体积=底面积×高×,将数据代入即可求得圆锥的体积。
【详解】(1)、(2)、(3)画图如下:
(4)3.14×2×2×3×
=3.14×4
=12.56(立方厘米)
以三角形的边为轴旋转一周形成的图形是(圆锥),它的高是(3)厘米,体积是(12.56)立方厘米。
【点睛】本题主要考了平面图形角旋转、平移及三角形高的画法及圆锥体积公式的灵活运用。
10.9.6厘米
【分析】根据圆柱的体积公式:V=πr2h,用3.14×42×5即可求出圆柱形钢件的体积,熔铸成一个圆锥形零件,体积不变,根据圆锥的体积公式:V=Sh,用零件的体积×3÷78.5即可求出零件的高度。据此解答。
【详解】3.14×42×5
=3.14×16×5
=251.2(立方厘米)
251.2×3÷78.5=9.6(厘米)
答:这件圆锥形零件的高是9.6厘米。
【点睛】本题主要考查了圆柱的体积公式和圆锥的体积公式的灵活应用,要熟练掌握公式。
11.(1)78.5m2
(2)141.3m2
(3)157000L
【分析】(1)水池的占地面积,就是这个圆柱形水池的底面积,由此利用底面直径求出这个圆柱的底面半径再代入圆的面积公式计算即可解答;
(2)抹水泥的面积就是这个圆柱水池的底面积加侧面积,利用圆柱的侧面积=底面周长×高计算出圆柱的侧面积,再加上底面积即可解答;
(3)要求这个水池能装多少水,就是求这个圆柱形水池的容积,利用圆柱的容积公式即可解答。
【详解】(1)10÷2=5(m)
3.14×52=78.5(m2)
答:水池的占地面积是78.5m2。
(2)3.14×10×2+78.5
=62.8+78.5
=141.3(m2)
答:抹水泥的部分是141.3m2。
(3)3.14×52×2
=3.14×25×2
=157(m3)
=157000(L)
答:这个水池能装157000L的水。
【点睛】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决。
12.4.5厘米
【分析】由题意可知:当甲杯中取出铁块后,水面下降部分水的体积就等于铁块的体积,即底面直径18厘米、高是2厘米的圆柱的体积;然后再除以乙杯的底面积,就是水位上升的高度.
【详解】3.14×(18÷2)2×2÷3.14÷(12÷2)2=4.5(厘米)
答:这时乙杯中的水位上升了4.5厘米.
13.10597.5千克
【分析】根据圆柱的体积公式,先列式计算出粮囤的体积,再将体积乘每立方米玉米的重量750千克,求出这个粮囤能装多少千克玉米。
【详解】3.14×1.52×2×750
=14.13×750
=10597.5(千克)
答:这个粮囤能装10597.5千克玉米。
【点睛】本题考查了圆柱的体积,圆柱的体积=底面积×高。
14.82.425dm2 78.5L
【详解】3.14×2.5×2×4+3.14×2.52=82.425(dm2)
3.14×2.52×4=78.5(dm3)=78.5(L)
答:做这个鱼缸至少需要82.425 dm2的玻璃,这个鱼缸最多能装水78.5 L.
15.565.2毫升
【分析】瓶子的两种放法,无水部分的容积是不变的,将右图中无水部分的圆柱移到左图,替换不规则的无水部分,则求瓶子的容积转化成求底面直径6cm,高(12+8)cm的圆柱形瓶子的容积,根据圆柱的体积公式V=πr2h,代入数据计算,最后根据进率“1立方厘米=1毫升”换算单位。
【详解】6÷2=3(厘米)
3.14×32×(12+8)
=3.14×9×20
=3.14×180
=565.2(立方厘米)
565.2立方厘米=565.2毫升
答:这个瓶子的容积是565.2毫升。
【点睛】明确瓶子倒置后无水部分的容积和正放时无水部分的容积相等是解题的关键。
16.(1)B;2;3
(2)9.42立方分米
(3)21.98平方分米
【分析】(1)因为用长方形铁皮作为圆柱的侧面,所以在此题中长方形的宽为圆柱的高,长方形的长为圆柱的底面周长,底面周长公式为:C=πd,求出直径,再将出4张铁皮较短的边与底面直径比较,从而决定选择哪一张。
(2)圆柱的体积公式为:V=Sh=πrh。
(3)因为此圆柱形水桶是无盖的,所以水与桶接触的面也就是一个底面和圆柱的侧面。
【详解】(1)圆柱的底面直径为:6.28÷3.14=2(dm),B中的边长恰好等于圆的直径,所以B铁皮作水桶的底最合适。水桶的底面直径是2,水桶高3。
(2)3.14×(2÷2)×3
=3.14×3
=9.42(立方分米)
答:这个水桶的容积为9.42立方分米。
(3)3.14×(2÷2)+6.28×3
=3.14+18.84
=21.98(平方分米)
答:盛满水后,水与桶接触的面一共有21.98平方分米。
【点睛】掌握圆柱的体积公式和侧面积公式是解决本题的关键。
17.5杯
【分析】先分别求出饮料盒里果汁的体积和茶杯的容积,再用除法计算.
【详解】30×20×6=3600(立方厘米)
3.14×(10÷2)2×8=628(立方厘米)
3600÷628≈5(杯)
答:能倒满5杯.
18.30分
【详解】1.5×0.6×0.4=0.36(m3) 0.36m3=360000cm3 40m=4000cm 360000÷(3×4000)=30(分)
19.2250
【详解】试题分析:因为两个圆柱的高一定,体积与底面积成正比,也与半径的平方成正比,所以两个圆柱的体积比为:22:52=4:25,那么360是第二个圆柱的体积的,根据分数除法的意义,那么第二个圆柱的体积是:360=2250(立方厘米),据此解答.
解:两个圆柱的体积比为:22:52=4:25,
360=2250(立方厘米);
答:第二个圆柱的体积是2250立方厘米.
点评:本题考查了比的灵活应用,关键是求出两个圆柱的体积的比,继而转化为两个量的分率关系,然后根据分数除法的意义解答即可.
20.31.4dm2;12.56dm3
【分析】由图可知,圆柱的底面直径为(4÷2)dm,计算出圆柱的底面半径,圆柱的高为4dm,利用和求出圆柱的表面积和体积,据此解答。
【详解】半径:4÷2÷2
=2÷2
=1(dm)
表面积:3.14×(4÷2)×4+2×3.14×12
=3.14×2×4+2×3.14×12
=6.28×4+6.28
=25.12+6.28
=31.4(dm2)
体积:3.14×12×4
=3.14×4
=12.56(dm3)
答:圆柱的表面积是31.4dm2;体积是12.56dm3。
【点睛】本题主要考查圆柱表面积和体积的应用,熟记公式是解答题目的关键。
21.1032立方厘米
【详解】(10×2)×(10×2)×12﹣3.14××12×4
=20×20×12﹣3.14×25×12×4
=4800﹣3768
=1032(立方厘米)
答:这个纸盒中空隙部分的体积是1032立方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
