2.6 一元一次不等式组第1课时 课件(共27张PPT)-八年级数学下册同步精品课堂(北师大版)
文档属性
| 名称 | 2.6 一元一次不等式组第1课时 课件(共27张PPT)-八年级数学下册同步精品课堂(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 701.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-16 05:35:55 | ||
图片预览








文档简介
北师大版 数学 八年级下册
第1课时
第二章 一元一次不等式与一元一次不等式组
6 一元一次不等式组
学习目标
1.通过具体操作,在解一元一次不等式组的过程中形成正确的解不等式的思路与方法;(重点、难点)
2.掌握将一元一次不等式组的解集在数轴上正确的表示.
复习回顾
解一元一次不等式的一般步骤:
①去分母——不等式性质2或3;
②去括号——去括号法则和分配律;
③移项——移项法则(不等式性质1);
④合并同类项——合并同类项法则;
⑤把系数化成1——不等式基本性质2或性质3.
注意:在①和⑤中,如果乘数或除数是负数,要把不等号的方向改变.
②当每月比原计划少烧5吨煤时, 实际每月烧______吨煤,根据取暖用煤总量不足68吨,可得不等式__________.
一、创设情境,引入新知
问题:某校今年冬季烧煤取暖时间为4个月,如果每月比计划多烧5吨煤,那么取暖用煤量将超过100吨;如果每月比计划少烧5吨煤,那么取暖用煤总量不足68吨.若该校计划每月烧煤x吨,则x满足怎样的关系式?
分析:①当每月比原计划多烧5吨煤时, 每月实际烧煤 吨.根据取暖用煤量将超过100吨,可得不等式____________;
(x+5)
4(x+5)>100
(x-5)
4(x-5)<68
思考:x同时满足几个条件?
二、自主合作,探究新知
探究一:一元一次不等式组的概念
由题意可得,未知数x同时满足①②两个条件.把①②两个不等式合在一起,就组成一个一元一次不等式组,记作:
4(x+5)>100, ①
4(x-5)<68. ②
问题:某校今年冬季烧煤取暖时间为4个月,如果每月比计划多烧5吨煤,那么取暖用煤量将超过100吨;如果每月比计划少烧5吨煤,那么取暖用煤总量不足68吨.若该校计划每月烧煤x吨,则x满足怎样的关系式?
二、自主合作,探究新知
知识要点
一般地,关于同一个未知数的几个一元一次不等式合在一起, 就组成一个一元一次不等式组.
一元一次不等式组的概念:
例1 判断下列是否为一元一次不等式组:
二、自主合作,探究新知
×
×
√
√
典型例题
二、自主合作,探究新知
探究二:一元一次不等式组的解集
(1)可得不等式组 ????????????????+????????????(?????????????)≥????????????????, ????????+????(?????????????)≤????????,
?
想一想:(1)在习题2.1第3题中,如果要配制的饮料同时满足两个小题的条件,那么你能列出一个不等式组吗?
(2)你能尝试找出符合上面一元一次不等式组的未知数的值吗?与同伴交流(将未知数的值在数轴上表示出来).
(2)分析:类比方程组的求解,不等式组中的各个不等式解集的公共部分,就是不等式组中的未知数的取值范围.
二、自主合作,探究新知
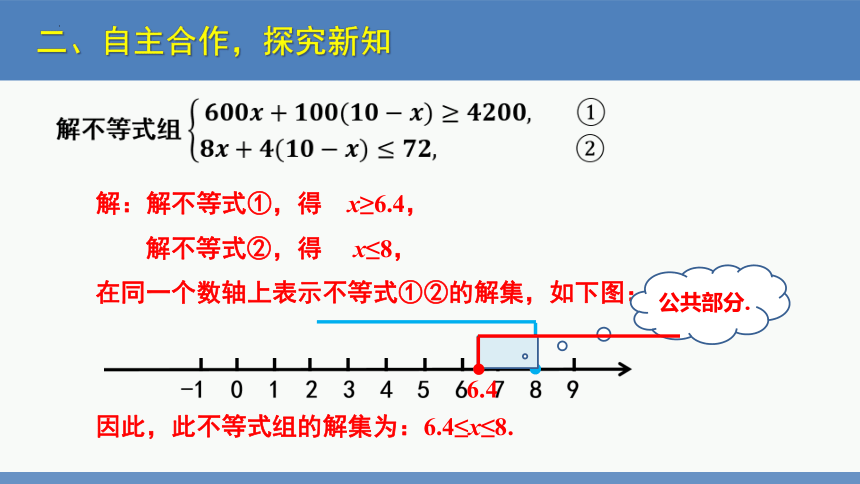
解:解不等式①,得 x≥6.4,
解不等式②,得 x≤8,
解不等式组 ????????????????+??????????(?????????????)≥????????????????, ①????????+????(?????????????)≤????????, ②
?
因此,此不等式组的解集为:6.4≤x≤8.
在同一个数轴上表示不等式①②的解集,如下图:
公共部分.
6.4
二、自主合作,探究新知
求不等式组的解集的过程,叫作解不等式组.
知识要点
一元一次不等式组的解集:
一元一次不等式组中各个不等式的解集的公共部分,叫做这个一元一次不等式组的解集.
解不等式组:
在同一个数轴上表示不等式①②的解集,如下图:
二、自主合作,探究新知
探究三:一元一次不等式组的解法
做一做:不等式组 ?????????????>?????, ?????????????
公共部分.
①
②
????????
?
标注序号
分别求解
在数轴上找出公共部分
写出不等式组的解集
解:解不等式①,得 x>????????,
解不等式②,得 x<6,
?
因此,原不等式组的解集为:????????<x<6.
?
二、自主合作,探究新知
解一元一次不等式组的一般步骤:
1.分别求出这个不等式组中各个不等式的解集;
2.利用数轴找寻这些不等式的解集的公共部分,即求出了这个不等式组的解集;若这些不等式的解集没有公共部分,则这个不等式组无解;
3.写出这个不等式组的解集.
知识要点
二、自主合作,探究新知
解不等式②,得
x >4.
解: 解不等式①,得
x >2.
例1. 解不等式组:
①
②
把不等式①、②的解集在数轴上表示出来,如图:
所以,这个不等式组的解集是x >4.
典型例题
二、自主合作,探究新知
议一议:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况?
a b
a b
a b
a b
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
xa无解
(1)
(2)
(3)
(4)
解集是___________;
解集是___________;
解集是___________;
解集是___________.
例2. 求下列不等式组的解集:
二、自主合作,探究新知
无解
-1
0
6
0
-4
0
-1
2
-2
0
2
典型例题
x≥0
-2≤x<2
x<-1
例3:如果关于x的不等式组?????????>????, ?????????????≥????(?????????),有解,那么m的取值范围为 .
?
二、自主合作,探究新知
m<3
典型例题
解析:由x-m>0得x>m,
由2x-3≥3(x-2)得x≤3.因为该不等式组有解,所以m<3.
2.一个不等式组中的两个不等式的解集如图所示,则这个不等式组的解集为( )
A.-21.下列是一元一次不等式组的是( )
A.????+????>????,????????+????>????, B.????+????????>????,?????????????≤????,
C.????>????,?????
三、即学即练,应用知识
C
D
4.已知点A(x+3,2x-4)在第四象限,则x的取值范围是( )A.-3-3 C.x<2 D.x>2
3.不等式组????+????≥?????,?????????
三、即学即练,应用知识
D
A
6.不等式组?????????≥????,????????>?????????,的最小整数解是 .
?
7.若不等式组????+????????????,的解集是x>4,则m的取值范围是 .
?
5.不等式组????????≤????????+????,①????????+????≥?????.②的解集为 .
?
三、即学即练,应用知识
0
m≤4
-3≤x≤1
三、即学即练,应用知识
解: (1)????????>?????????,①????+????????????,由②得x>1.故不等式组的解集为x>1.不等式组的解集在数轴上表示如图:
?
解: (2)?????????????>????, ① ?????????????5,由②得x<8.故不等式组的解集为5?
8.解下列不等式组,并把解集表示在数轴上.
(1)????????>?????????,????+????????, ??????????????
四、课堂小结
一般地,关于同一个未知数的几个一元一次不等式合在一起, 就组成一个一元一次不等式组.
一元一次不等式组
概念
解集
解法
解不等式组
一元一次不等式组中各个不等式的解集的公共部分,叫做这个一元一次不等式组的解集.
求不等式组的解集的过程,叫作解不等式组.
①标注序号,②分别求解,③在数轴上找出公共部分,④写出不等式组的解集.
解的情况:同大取大,同小取小,大小小大中间找,大大小小无处找.
2.不等式组????≥?????,????>????, 的解集在数轴上的表示为( )
?
1.小明要制作一个长方形的相片框架(长、宽不等),这个框架的长为25 cm,面积不小于500 cm2,则宽x(cm)应满足的不等式组为( )
五、当堂达标检测
A
A
3.不等式组?????????-2 C.-3≤x<-2 D.x≤-3
?
4.某不等式组的解集在数轴上的表示如图所示,则这个不等式组可能是( )
五、当堂达标检测
C
C
5.不等式组????????+????>????,?????????
五、当堂达标检测
6.在平面直角坐标系中,若点P(2x+6,5x)在第四象限,则x的取值范围是 .
-3<x<0
3
7.若关于x的不等式组的整数解共有3个,则m的取值范围是 .
5五、当堂达标检测
8.解不等式组??????????????
解: ??????????????
五、当堂达标检测
9.若关于x,y的二元一次方程组?????????=?????????,????+????=????????+????中,x的值为负数,y的值为正数,求m的取值范围.
?
解: 解关于x,y的二元一次方程组?????????=?????????,????+????=????????+????得????=?????????????,????=????+????,因为x的值为负数,y的值为正数,所以?????????????????,解这个不等式组,得-4?
教材习题2.8.
六、布置作业
第1课时
第二章 一元一次不等式与一元一次不等式组
6 一元一次不等式组
学习目标
1.通过具体操作,在解一元一次不等式组的过程中形成正确的解不等式的思路与方法;(重点、难点)
2.掌握将一元一次不等式组的解集在数轴上正确的表示.
复习回顾
解一元一次不等式的一般步骤:
①去分母——不等式性质2或3;
②去括号——去括号法则和分配律;
③移项——移项法则(不等式性质1);
④合并同类项——合并同类项法则;
⑤把系数化成1——不等式基本性质2或性质3.
注意:在①和⑤中,如果乘数或除数是负数,要把不等号的方向改变.
②当每月比原计划少烧5吨煤时, 实际每月烧______吨煤,根据取暖用煤总量不足68吨,可得不等式__________.
一、创设情境,引入新知
问题:某校今年冬季烧煤取暖时间为4个月,如果每月比计划多烧5吨煤,那么取暖用煤量将超过100吨;如果每月比计划少烧5吨煤,那么取暖用煤总量不足68吨.若该校计划每月烧煤x吨,则x满足怎样的关系式?
分析:①当每月比原计划多烧5吨煤时, 每月实际烧煤 吨.根据取暖用煤量将超过100吨,可得不等式____________;
(x+5)
4(x+5)>100
(x-5)
4(x-5)<68
思考:x同时满足几个条件?
二、自主合作,探究新知
探究一:一元一次不等式组的概念
由题意可得,未知数x同时满足①②两个条件.把①②两个不等式合在一起,就组成一个一元一次不等式组,记作:
4(x+5)>100, ①
4(x-5)<68. ②
问题:某校今年冬季烧煤取暖时间为4个月,如果每月比计划多烧5吨煤,那么取暖用煤量将超过100吨;如果每月比计划少烧5吨煤,那么取暖用煤总量不足68吨.若该校计划每月烧煤x吨,则x满足怎样的关系式?
二、自主合作,探究新知
知识要点
一般地,关于同一个未知数的几个一元一次不等式合在一起, 就组成一个一元一次不等式组.
一元一次不等式组的概念:
例1 判断下列是否为一元一次不等式组:
二、自主合作,探究新知
×
×
√
√
典型例题
二、自主合作,探究新知
探究二:一元一次不等式组的解集
(1)可得不等式组 ????????????????+????????????(?????????????)≥????????????????, ????????+????(?????????????)≤????????,
?
想一想:(1)在习题2.1第3题中,如果要配制的饮料同时满足两个小题的条件,那么你能列出一个不等式组吗?
(2)你能尝试找出符合上面一元一次不等式组的未知数的值吗?与同伴交流(将未知数的值在数轴上表示出来).
(2)分析:类比方程组的求解,不等式组中的各个不等式解集的公共部分,就是不等式组中的未知数的取值范围.
二、自主合作,探究新知
解:解不等式①,得 x≥6.4,
解不等式②,得 x≤8,
解不等式组 ????????????????+??????????(?????????????)≥????????????????, ①????????+????(?????????????)≤????????, ②
?
因此,此不等式组的解集为:6.4≤x≤8.
在同一个数轴上表示不等式①②的解集,如下图:
公共部分.
6.4
二、自主合作,探究新知
求不等式组的解集的过程,叫作解不等式组.
知识要点
一元一次不等式组的解集:
一元一次不等式组中各个不等式的解集的公共部分,叫做这个一元一次不等式组的解集.
解不等式组:
在同一个数轴上表示不等式①②的解集,如下图:
二、自主合作,探究新知
探究三:一元一次不等式组的解法
做一做:不等式组 ?????????????>?????, ?????????????
公共部分.
①
②
????????
?
标注序号
分别求解
在数轴上找出公共部分
写出不等式组的解集
解:解不等式①,得 x>????????,
解不等式②,得 x<6,
?
因此,原不等式组的解集为:????????<x<6.
?
二、自主合作,探究新知
解一元一次不等式组的一般步骤:
1.分别求出这个不等式组中各个不等式的解集;
2.利用数轴找寻这些不等式的解集的公共部分,即求出了这个不等式组的解集;若这些不等式的解集没有公共部分,则这个不等式组无解;
3.写出这个不等式组的解集.
知识要点
二、自主合作,探究新知
解不等式②,得
x >4.
解: 解不等式①,得
x >2.
例1. 解不等式组:
①
②
把不等式①、②的解集在数轴上表示出来,如图:
所以,这个不等式组的解集是x >4.
典型例题
二、自主合作,探究新知
议一议:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况?
a b
a b
a b
a b
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
xa
(1)
(2)
(3)
(4)
解集是___________;
解集是___________;
解集是___________;
解集是___________.
例2. 求下列不等式组的解集:
二、自主合作,探究新知
无解
-1
0
6
0
-4
0
-1
2
-2
0
2
典型例题
x≥0
-2≤x<2
x<-1
例3:如果关于x的不等式组?????????>????, ?????????????≥????(?????????),有解,那么m的取值范围为 .
?
二、自主合作,探究新知
m<3
典型例题
解析:由x-m>0得x>m,
由2x-3≥3(x-2)得x≤3.因为该不等式组有解,所以m<3.
2.一个不等式组中的两个不等式的解集如图所示,则这个不等式组的解集为( )
A.-2
A.????+????>????,????????+????>????, B.????+????????>????,?????????????≤????,
C.????>????,?????
三、即学即练,应用知识
C
D
4.已知点A(x+3,2x-4)在第四象限,则x的取值范围是( )A.-3
3.不等式组????+????≥?????,?????????
三、即学即练,应用知识
D
A
6.不等式组?????????≥????,????????>?????????,的最小整数解是 .
?
7.若不等式组????+????????????,的解集是x>4,则m的取值范围是 .
?
5.不等式组????????≤????????+????,①????????+????≥?????.②的解集为 .
?
三、即学即练,应用知识
0
m≤4
-3≤x≤1
三、即学即练,应用知识
解: (1)????????>?????????,①????+????????????,由②得x>1.故不等式组的解集为x>1.不等式组的解集在数轴上表示如图:
?
解: (2)?????????????>????, ① ?????????????5,由②得x<8.故不等式组的解集为5
8.解下列不等式组,并把解集表示在数轴上.
(1)????????>?????????,????+????????, ??????????????
四、课堂小结
一般地,关于同一个未知数的几个一元一次不等式合在一起, 就组成一个一元一次不等式组.
一元一次不等式组
概念
解集
解法
解不等式组
一元一次不等式组中各个不等式的解集的公共部分,叫做这个一元一次不等式组的解集.
求不等式组的解集的过程,叫作解不等式组.
①标注序号,②分别求解,③在数轴上找出公共部分,④写出不等式组的解集.
解的情况:同大取大,同小取小,大小小大中间找,大大小小无处找.
2.不等式组????≥?????,????>????, 的解集在数轴上的表示为( )
?
1.小明要制作一个长方形的相片框架(长、宽不等),这个框架的长为25 cm,面积不小于500 cm2,则宽x(cm)应满足的不等式组为( )
五、当堂达标检测
A
A
3.不等式组?????????-2 C.-3≤x<-2 D.x≤-3
?
4.某不等式组的解集在数轴上的表示如图所示,则这个不等式组可能是( )
五、当堂达标检测
C
C
5.不等式组????????+????>????,?????????
五、当堂达标检测
6.在平面直角坐标系中,若点P(2x+6,5x)在第四象限,则x的取值范围是 .
-3<x<0
3
7.若关于x的不等式组的整数解共有3个,则m的取值范围是 .
5
8.解不等式组??????????????
解: ??????????????
五、当堂达标检测
9.若关于x,y的二元一次方程组?????????=?????????,????+????=????????+????中,x的值为负数,y的值为正数,求m的取值范围.
?
解: 解关于x,y的二元一次方程组?????????=?????????,????+????=????????+????得????=?????????????,????=????+????,因为x的值为负数,y的值为正数,所以?????????????????,解这个不等式组,得-4
教材习题2.8.
六、布置作业
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
