9.4 矩形、菱形、正方形(第4课时) 课件(共28张PPT)-八年级数学下册同步精品课堂(苏科版)
文档属性
| 名称 | 9.4 矩形、菱形、正方形(第4课时) 课件(共28张PPT)-八年级数学下册同步精品课堂(苏科版) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-16 05:34:23 | ||
图片预览






文档简介
第9章 · 中心对称图形——平行四边形
9.4 矩形、菱形、正方形(4)
第4课时 菱形的判定
学习目标
1.探索并证明菱形的判定定理;
2.能应用菱形的判定定理解决问题,进一步体会推理的基本方法.
将2张等宽的矩形纸片叠合在一起(如图),请你猜想它是什么特殊的四边形?请动手叠一叠.
问题情境
B
A
D
C
1. 我们知道,菱形的四条边都相等.反过来,四条边都相等的四边形是菱形吗?
思考与探索
证明:∵AB=BC=CD=AD,
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.
已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
B
A
D
C
思考与探索
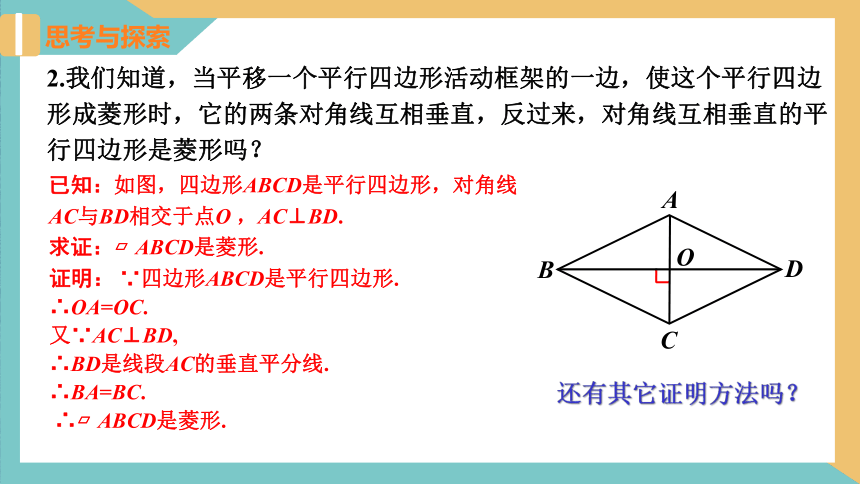
2.我们知道,当平移一个平行四边形活动框架的一边,使这个平行四边形成菱形时,它的两条对角线互相垂直,反过来,对角线互相垂直的平行四边形是菱形吗?
B
A
D
C
O
已知:如图,四边形ABCD是平行四边形,对角线
AC与BD相交于点O ,AC⊥BD.
求证:?ABCD是菱形.
证明: ∵四边形ABCD是平行四边形.
∴OA=OC.
又∵AC⊥BD,
∴BD是线段AC的垂直平分线.
∴BA=BC.
∴?ABCD是菱形.
还有其它证明方法吗?
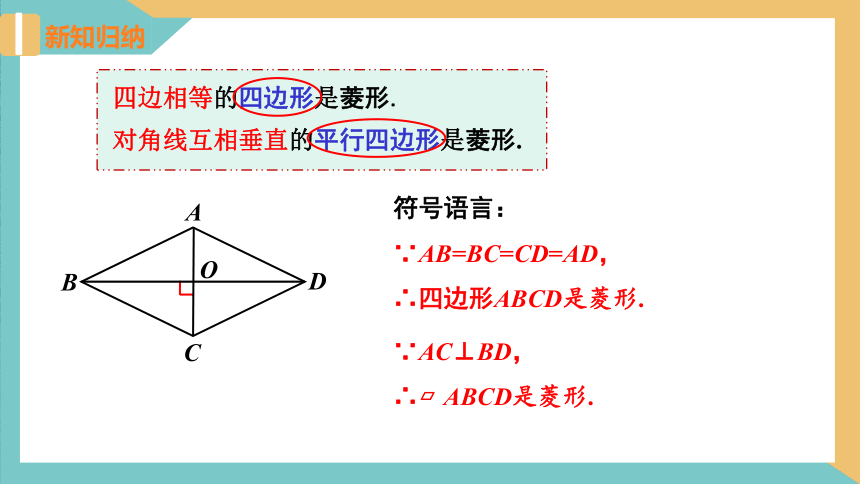
新知归纳
四边相等的四边形是菱形.
对角线互相垂直的平行四边形是菱形.
符号语言:
∵AB=BC=CD=AD,
∴四边形ABCD是菱形.
∵AC⊥BD,
∴?ABCD是菱形.
B
A
D
C
O
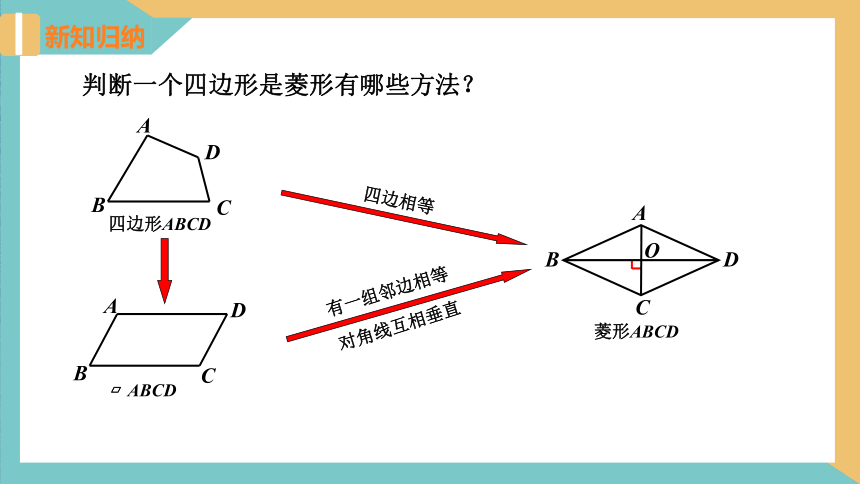
新知归纳
A
B
C
D
四边形ABCD
四边相等
B
D
?ABCD
A
C
有一组邻边相等
对角线互相垂直
判断一个四边形是菱形有哪些方法?
B
A
D
C
O
菱形ABCD
对角线互相垂直的四边形是菱形吗?
讨论与交流
新知巩固
①有一组邻边相等的四边形是菱形. ( )
②四条边都相等的四边形是菱形. ( )
③对角线互相平分且有一组邻边相等的四边形是菱形. ( )
④对角线互相垂直的四边形是菱形. ( )
⑤对角线互相垂直平分的四边形是菱形. ( )
判断:
×
√
√
×
√
新知应用
B
A
D
C
猜想:四边形ABCD是菱形.
易知四边形ABCD是平行四边形,只需证一组邻边相等或对角线互相垂直即可.
E
F
证明:由两个纸条是矩形可得AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∴∠B=∠D,
过A作AE⊥BC,AF⊥CD,垂足为E、F,
∵两张矩形纸条宽度相同,
∴AE=AF,
在△ABE和△ADF中,
∠????????????=∠????????????=????????°∠????=∠????????????=????????,
∴△ABE≌△ADF(AAS),
∴AB=AD,
∴四边形ABCD是菱形.
?
例题讲解
例1 已知:如图,在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与边AD、BC分别相交于点E、F.求证:四边形AFCE是菱形.
O
B
A
D
C
F
E
1
2
证法1:∵AD∥BC,
∴∠1=∠2.
∵ EF垂直平分AC,
∴ OA=OC,∠AOE=∠COF,
∴△AOE≌△COF.
∴ OE=OF.
∴四边形AFCE是平行四边形.
又∵EF⊥AC,
∴?AFCE是菱形.
∵ EF垂直平分AC,
∴AE=CE,
∴?AFCE是菱形.
例题讲解
例1 已知:如图,在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与边AD、BC分别相交于点E、F.求证:四边形AFCE是菱形.
O
B
A
D
C
F
E
1
2
证法2:∵AD∥BC,
∴∠1=∠2.
∵ EF垂直平分AC,
∴ OA=OC,∠AOE=∠COF,
∴△AOE≌△COF.
∴ AE=CF.
∵ EF垂直平分AC,
∴AE=CE,AF=CF.
∴AE=CE=AF=CF.
∴四边形AFCE是菱形.
1. 如图,E、F、G、H分别是矩形ABCD各边的中点,四边形EFGH是怎样的特殊四边形?证明你的结论?
解:四边形EFGH是菱形.
证明:∵四边形ABCD是矩形,
∴AD=BC,AB=DC,
∠A=∠B=∠C=∠D=90°
∵E、F、G、H分别是矩形的各边中点
∴AH=DH=BF=CF,AE=BE=DG=CG
∴△AEH≌△BEF≌△CGF≌△DGH (SAS)
∴EH=EF=GF=GH,
∴四边形EFGH是菱形.
A
B
C
D
G
F
H
E
新知巩固
中点四边形
新知巩固
2. 已知:如图,矩形ABCD的对角线AC、BD相交于点O,BE∥AC,CE∥DB.
求证:四边形OBEC是菱形.
A
B
C
D
O
E
证明:∵BE∥AC,CE∥DB,
∴四边形OBEC是平行四边形.
∵四边形ABCD是矩形,
∴AC=BD,AO=CO=????????AC,BO=DO=????????BD,
∴AO=BO.
∴四边形OBEC是菱形.
?
新知巩固
3. 已知:如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.
求证:四边形ABEF是菱形.
A
B
C
D
E
F
A
B
C
证明:∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠AFB=∠EBF,
∠BAD+∠ABC=180°.
∵AE、BF分别是∠BAD和∠ABC的平分线,
∴∠BAE=????????∠BAD,∠ABF= ∠EBF=????????∠ABC,
∴∠AFB=∠ABF,
∴AB=AF.
同理,AB=BE.
∴AF=BE.
∵AD//BC,
∴四边形 ABEF是平行四边形.
∵∠BAE+∠ABF=????????∠BAD+????????∠ABC=????????×180°=90°,
∴AE⊥BF,
∴四边形 ABEF是菱形.
?
课堂小结
9.4 矩形、菱形、正方形(4)
有一组邻边相等的平行四边形
四边相等的四边形
对角线互相垂直的平行四边形
1. 下列命题中正确的是( )
A. 一组邻边相等的四边形是菱形
B. 一条对角线平分一组内角的平行四边形是菱形
C. 对角线垂直的四边形是菱形
D. 对角线相等的四边形是菱形
当堂检测
B
当堂检测
2. 如图,在△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是( )
A. AB=AC B. AD=BD
C. BE⊥AC D. BE平分∠ABC
D
D
E
F
A
B
C
当堂检测
3.在△ABC中,AD平分∠BAC,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于AD的一半长为半径在AD两侧作弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
则可以得到四边形AEDF的形状( )
A.仅仅只是平行四边形 B.是矩形
C.是菱形 D.无法判断
C
当堂检测
第4课时 菱形的判定
4. 如图,四边形ABCD的对角线互相垂直,且OB=OD,请你添加一个适当的条件__________________________________________________,
使四边形ABCD成为菱形.(只需添加一个即可)
答案不唯一,如OA=OC或AD=BC或AD∥BC或AB=BC等
B
A
D
C
O
当堂检测
5. 如图,矩形ABCD的对角线AC,BD相交于点O,DE∥AC,CE∥BD.若AC=10,则四边形OCED的周长是________.
20
E
A
B
C
D
O
当堂检测
6. 如图,四边形ABCD的对角线AC,BD相交于点O,且AO=OC=6 cm,BO=OD=8 cm,AB=10 cm,四边形ABCD是菱形吗?请说明理由.
B
A
D
C
O
解:四边形ABCD是菱形,理由如下:
∵AO=OC,BO=OD,
∴四边形ABCD是平行四边形.
∵AO=6 cm,BO=8 cm,AB=10 cm,
∴AO2+BO2=AB2,
∴△AOB是直角三角形,∠AOB=90°,
即AC⊥BD,
∴四边形ABCD是菱形.
当堂检测
7.如图,在矩形ABCD中,AB=4,BC=8,点E、F分别在边AD、BC上,BF=DE=3.
求证:四边形AFCE是菱形.
证明:∵四边形ABCD是矩形,
∴CD=AB=4,AD=BC=8
∠B=∠D=90°.
∵BF=DE=3,
∴在Rt△ABF中,由勾股定理得
AF=????????????+????????????=????????+????????=5.
同理得:CE=5,
∵CF=BC-BF=8-3=5,AE=AD-DE=8-3=5,
∴AF=CF=CE=AE,
∴四边形AFCE是菱形.
?
E
B
A
C
D
F
当堂检测
8. 如图,在?ABCD中,AC,BD交于点O,点E,F在AC上,AE=CF.(1)求证:四边形EBFD是平行四边形;
A
D
C
B
O
E
F
证明:在?ABCD中,OA=OC,OB=OD,
∵AE=CF,
∴OE=OF,
∴四边形EBFD是平行四边形.
当堂检测
8. 如图,在?ABCD中,AC,BD交于点O,点E,F在AC上,AE=CF.
(2)若∠BAC=∠DAC,求证:四边形EBFD是菱形.
证明:∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠BAC=∠DCA.
∵∠BAC=∠DAC,
∴∠DCA=∠DAC,
∴DA=DC,
∴平行四边形ABCD是菱形
∴AC⊥BD,
∴?EBFD是菱形.
A
D
C
B
O
E
F
9. 已知:如图,△ABC中,∠ACB=90°,CD是高,AE是角平分线,交CD于F,EG⊥AB,G是垂足,四边形CEGF是菱形吗?为什么?
A
D
C
B
E
F
G
证明:∵AE平分∠BAC
∠ACB=90°,EG⊥AB
∴CE=EG,∠AEG=∠AEC,
在△CEF和△GEF中,????????=????????, ∠????????????=∠????????????,????????=????????,
∴△CEF≌△GEF(SAS),
∴FG=CF,∠CFE=∠GFE,
∵CD⊥AB,EG⊥AB,∴CD∥EG,
∴∠CFE=∠GEF,
又∵∠CFE=∠GFE,∴∠CFE=∠CEF,∴CF=CE,
又∵FG=FC,CE=EG∴CF=CE=EG=FG,
∴四边形CEGF是菱形.
?
当堂检测
思维提升
1. 画一个菱形使它的两条对角线长分别是6cm,8cm.
3cm
4cm
2.如图,已知△ABD、△BCE、△ACF都是等边三角形. △ABC满足什么条件时,四边形ADEF是菱形?请说明理由.
A
D
C
B
E
F
解:∵△ABD和△BCE都是等边三角形,
∴AB=DB,BC=BE,∠DBA=∠EBC=60°
∴∠DBE+∠EBA=∠ABC+∠EBA,∴∠DBE=∠ABC.
在△ABC与△DBE中,
????????=????????, ∠????????????=∠????????????,????????=????????,
∴△ABC≌△DBE(SAS),
∴AC=DE.
∵△ACF是等边三角形,
∴AF=AC,
∴DE=AF.
同理可得:EF=AD,
∴四边形ADEF是平行四边形.
当△ABC满足AB=AC≠BC时,四边形ADEF是菱形.
?
思维提升
9.4 矩形、菱形、正方形(4)
第4课时 菱形的判定
学习目标
1.探索并证明菱形的判定定理;
2.能应用菱形的判定定理解决问题,进一步体会推理的基本方法.
将2张等宽的矩形纸片叠合在一起(如图),请你猜想它是什么特殊的四边形?请动手叠一叠.
问题情境
B
A
D
C
1. 我们知道,菱形的四条边都相等.反过来,四条边都相等的四边形是菱形吗?
思考与探索
证明:∵AB=BC=CD=AD,
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.
已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
B
A
D
C
思考与探索
2.我们知道,当平移一个平行四边形活动框架的一边,使这个平行四边形成菱形时,它的两条对角线互相垂直,反过来,对角线互相垂直的平行四边形是菱形吗?
B
A
D
C
O
已知:如图,四边形ABCD是平行四边形,对角线
AC与BD相交于点O ,AC⊥BD.
求证:?ABCD是菱形.
证明: ∵四边形ABCD是平行四边形.
∴OA=OC.
又∵AC⊥BD,
∴BD是线段AC的垂直平分线.
∴BA=BC.
∴?ABCD是菱形.
还有其它证明方法吗?
新知归纳
四边相等的四边形是菱形.
对角线互相垂直的平行四边形是菱形.
符号语言:
∵AB=BC=CD=AD,
∴四边形ABCD是菱形.
∵AC⊥BD,
∴?ABCD是菱形.
B
A
D
C
O
新知归纳
A
B
C
D
四边形ABCD
四边相等
B
D
?ABCD
A
C
有一组邻边相等
对角线互相垂直
判断一个四边形是菱形有哪些方法?
B
A
D
C
O
菱形ABCD
对角线互相垂直的四边形是菱形吗?
讨论与交流
新知巩固
①有一组邻边相等的四边形是菱形. ( )
②四条边都相等的四边形是菱形. ( )
③对角线互相平分且有一组邻边相等的四边形是菱形. ( )
④对角线互相垂直的四边形是菱形. ( )
⑤对角线互相垂直平分的四边形是菱形. ( )
判断:
×
√
√
×
√
新知应用
B
A
D
C
猜想:四边形ABCD是菱形.
易知四边形ABCD是平行四边形,只需证一组邻边相等或对角线互相垂直即可.
E
F
证明:由两个纸条是矩形可得AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∴∠B=∠D,
过A作AE⊥BC,AF⊥CD,垂足为E、F,
∵两张矩形纸条宽度相同,
∴AE=AF,
在△ABE和△ADF中,
∠????????????=∠????????????=????????°∠????=∠????????????=????????,
∴△ABE≌△ADF(AAS),
∴AB=AD,
∴四边形ABCD是菱形.
?
例题讲解
例1 已知:如图,在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与边AD、BC分别相交于点E、F.求证:四边形AFCE是菱形.
O
B
A
D
C
F
E
1
2
证法1:∵AD∥BC,
∴∠1=∠2.
∵ EF垂直平分AC,
∴ OA=OC,∠AOE=∠COF,
∴△AOE≌△COF.
∴ OE=OF.
∴四边形AFCE是平行四边形.
又∵EF⊥AC,
∴?AFCE是菱形.
∵ EF垂直平分AC,
∴AE=CE,
∴?AFCE是菱形.
例题讲解
例1 已知:如图,在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与边AD、BC分别相交于点E、F.求证:四边形AFCE是菱形.
O
B
A
D
C
F
E
1
2
证法2:∵AD∥BC,
∴∠1=∠2.
∵ EF垂直平分AC,
∴ OA=OC,∠AOE=∠COF,
∴△AOE≌△COF.
∴ AE=CF.
∵ EF垂直平分AC,
∴AE=CE,AF=CF.
∴AE=CE=AF=CF.
∴四边形AFCE是菱形.
1. 如图,E、F、G、H分别是矩形ABCD各边的中点,四边形EFGH是怎样的特殊四边形?证明你的结论?
解:四边形EFGH是菱形.
证明:∵四边形ABCD是矩形,
∴AD=BC,AB=DC,
∠A=∠B=∠C=∠D=90°
∵E、F、G、H分别是矩形的各边中点
∴AH=DH=BF=CF,AE=BE=DG=CG
∴△AEH≌△BEF≌△CGF≌△DGH (SAS)
∴EH=EF=GF=GH,
∴四边形EFGH是菱形.
A
B
C
D
G
F
H
E
新知巩固
中点四边形
新知巩固
2. 已知:如图,矩形ABCD的对角线AC、BD相交于点O,BE∥AC,CE∥DB.
求证:四边形OBEC是菱形.
A
B
C
D
O
E
证明:∵BE∥AC,CE∥DB,
∴四边形OBEC是平行四边形.
∵四边形ABCD是矩形,
∴AC=BD,AO=CO=????????AC,BO=DO=????????BD,
∴AO=BO.
∴四边形OBEC是菱形.
?
新知巩固
3. 已知:如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.
求证:四边形ABEF是菱形.
A
B
C
D
E
F
A
B
C
证明:∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠AFB=∠EBF,
∠BAD+∠ABC=180°.
∵AE、BF分别是∠BAD和∠ABC的平分线,
∴∠BAE=????????∠BAD,∠ABF= ∠EBF=????????∠ABC,
∴∠AFB=∠ABF,
∴AB=AF.
同理,AB=BE.
∴AF=BE.
∵AD//BC,
∴四边形 ABEF是平行四边形.
∵∠BAE+∠ABF=????????∠BAD+????????∠ABC=????????×180°=90°,
∴AE⊥BF,
∴四边形 ABEF是菱形.
?
课堂小结
9.4 矩形、菱形、正方形(4)
有一组邻边相等的平行四边形
四边相等的四边形
对角线互相垂直的平行四边形
1. 下列命题中正确的是( )
A. 一组邻边相等的四边形是菱形
B. 一条对角线平分一组内角的平行四边形是菱形
C. 对角线垂直的四边形是菱形
D. 对角线相等的四边形是菱形
当堂检测
B
当堂检测
2. 如图,在△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是( )
A. AB=AC B. AD=BD
C. BE⊥AC D. BE平分∠ABC
D
D
E
F
A
B
C
当堂检测
3.在△ABC中,AD平分∠BAC,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于AD的一半长为半径在AD两侧作弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
则可以得到四边形AEDF的形状( )
A.仅仅只是平行四边形 B.是矩形
C.是菱形 D.无法判断
C
当堂检测
第4课时 菱形的判定
4. 如图,四边形ABCD的对角线互相垂直,且OB=OD,请你添加一个适当的条件__________________________________________________,
使四边形ABCD成为菱形.(只需添加一个即可)
答案不唯一,如OA=OC或AD=BC或AD∥BC或AB=BC等
B
A
D
C
O
当堂检测
5. 如图,矩形ABCD的对角线AC,BD相交于点O,DE∥AC,CE∥BD.若AC=10,则四边形OCED的周长是________.
20
E
A
B
C
D
O
当堂检测
6. 如图,四边形ABCD的对角线AC,BD相交于点O,且AO=OC=6 cm,BO=OD=8 cm,AB=10 cm,四边形ABCD是菱形吗?请说明理由.
B
A
D
C
O
解:四边形ABCD是菱形,理由如下:
∵AO=OC,BO=OD,
∴四边形ABCD是平行四边形.
∵AO=6 cm,BO=8 cm,AB=10 cm,
∴AO2+BO2=AB2,
∴△AOB是直角三角形,∠AOB=90°,
即AC⊥BD,
∴四边形ABCD是菱形.
当堂检测
7.如图,在矩形ABCD中,AB=4,BC=8,点E、F分别在边AD、BC上,BF=DE=3.
求证:四边形AFCE是菱形.
证明:∵四边形ABCD是矩形,
∴CD=AB=4,AD=BC=8
∠B=∠D=90°.
∵BF=DE=3,
∴在Rt△ABF中,由勾股定理得
AF=????????????+????????????=????????+????????=5.
同理得:CE=5,
∵CF=BC-BF=8-3=5,AE=AD-DE=8-3=5,
∴AF=CF=CE=AE,
∴四边形AFCE是菱形.
?
E
B
A
C
D
F
当堂检测
8. 如图,在?ABCD中,AC,BD交于点O,点E,F在AC上,AE=CF.(1)求证:四边形EBFD是平行四边形;
A
D
C
B
O
E
F
证明:在?ABCD中,OA=OC,OB=OD,
∵AE=CF,
∴OE=OF,
∴四边形EBFD是平行四边形.
当堂检测
8. 如图,在?ABCD中,AC,BD交于点O,点E,F在AC上,AE=CF.
(2)若∠BAC=∠DAC,求证:四边形EBFD是菱形.
证明:∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠BAC=∠DCA.
∵∠BAC=∠DAC,
∴∠DCA=∠DAC,
∴DA=DC,
∴平行四边形ABCD是菱形
∴AC⊥BD,
∴?EBFD是菱形.
A
D
C
B
O
E
F
9. 已知:如图,△ABC中,∠ACB=90°,CD是高,AE是角平分线,交CD于F,EG⊥AB,G是垂足,四边形CEGF是菱形吗?为什么?
A
D
C
B
E
F
G
证明:∵AE平分∠BAC
∠ACB=90°,EG⊥AB
∴CE=EG,∠AEG=∠AEC,
在△CEF和△GEF中,????????=????????, ∠????????????=∠????????????,????????=????????,
∴△CEF≌△GEF(SAS),
∴FG=CF,∠CFE=∠GFE,
∵CD⊥AB,EG⊥AB,∴CD∥EG,
∴∠CFE=∠GEF,
又∵∠CFE=∠GFE,∴∠CFE=∠CEF,∴CF=CE,
又∵FG=FC,CE=EG∴CF=CE=EG=FG,
∴四边形CEGF是菱形.
?
当堂检测
思维提升
1. 画一个菱形使它的两条对角线长分别是6cm,8cm.
3cm
4cm
2.如图,已知△ABD、△BCE、△ACF都是等边三角形. △ABC满足什么条件时,四边形ADEF是菱形?请说明理由.
A
D
C
B
E
F
解:∵△ABD和△BCE都是等边三角形,
∴AB=DB,BC=BE,∠DBA=∠EBC=60°
∴∠DBE+∠EBA=∠ABC+∠EBA,∴∠DBE=∠ABC.
在△ABC与△DBE中,
????????=????????, ∠????????????=∠????????????,????????=????????,
∴△ABC≌△DBE(SAS),
∴AC=DE.
∵△ACF是等边三角形,
∴AF=AC,
∴DE=AF.
同理可得:EF=AD,
∴四边形ADEF是平行四边形.
当△ABC满足AB=AC≠BC时,四边形ADEF是菱形.
?
思维提升
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
