17.3 一次函数(第3课时) 课件(共26张PPT)-八年级数学下册同步精品课堂(华东师大版)
文档属性
| 名称 | 17.3 一次函数(第3课时) 课件(共26张PPT)-八年级数学下册同步精品课堂(华东师大版) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-16 00:00:00 | ||
图片预览







文档简介
17.3 一次函数
第3课时 一次函数的性质
数学(华东师大版)
八年级 下册
第17章 函数及其图象
学习目标
1、掌握一次函数的性质;
2、能灵活运用一次函数的图象与性质解答有关问题;
温故知新
1.一次函数图象有什么特点?
2.作出一次函数图象需要描出几个点?
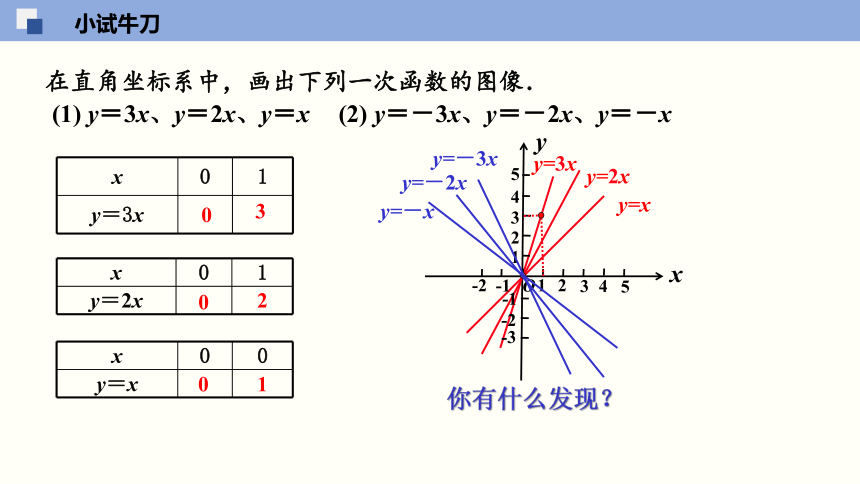
只需要描出2个点.
一次函数y=kx+b的图象是一条直线,直线上所有点的坐标都满足表达式y=kx+b.
一般选直线与两坐标轴的两交点,即(0,b)和( ,0).
小试牛刀
在直角坐标系中,画出下列一次函数的图像.
(1) y=3x、y=2x、y=x
{5940675A-B579-460E-94D1-54222C63F5DA}x
0
1
y=3x
{5940675A-B579-460E-94D1-54222C63F5DA}x
0
1
y=2x
0
3
0
2
{5940675A-B579-460E-94D1-54222C63F5DA}x
0
0
y=x
0
1
1
2
y
3
4
5
-2
-3
4
5
3
2
O
x
1
-1
-2
-1
y=2x
y=3x
y=x
(2) y=-3x、y=-2x、y=-x
y=-3x
y=-2x
y=-x
你有什么发现?
讲授新课
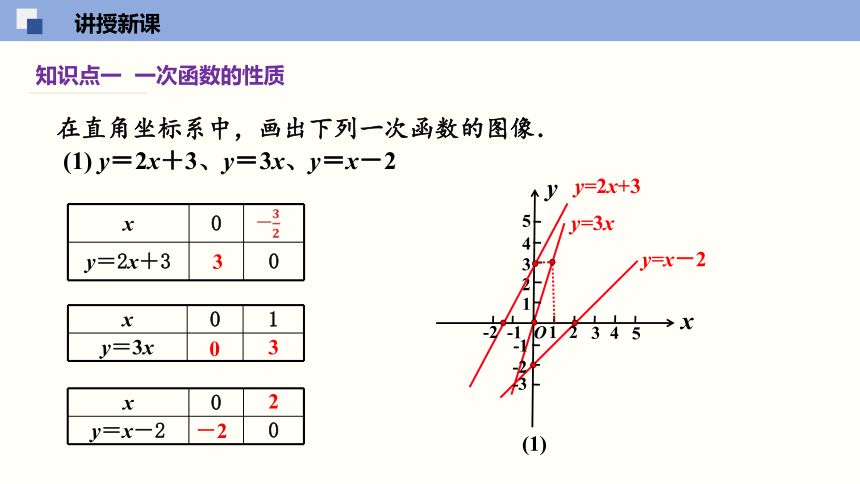
知识点一 一次函数的性质
在直角坐标系中,画出下列一次函数的图像.
(1) y=2x+3、y=3x、y=x-2
{5940675A-B579-460E-94D1-54222C63F5DA}x
0
y=2x+3
0
{5940675A-B579-460E-94D1-54222C63F5DA}x
0
1
y=3x
3
-????????
?
0
3
{5940675A-B579-460E-94D1-54222C63F5DA}x
0
y=x-2
0
-2
2
1
2
y
3
4
5
-2
-3
4
5
3
2
O
x
1
-1
-2
-1
y=2x+3
y=3x
y=x-2
(1)
讲授新课
1
2
y
3
4
5
-2
-3
在直角坐标系中,画出下列一次函数的图像.
(2) y=-x+2、y=-2x、y=-????????x-1
?
{5940675A-B579-460E-94D1-54222C63F5DA}x
0
y=-x+2
0
{5940675A-B579-460E-94D1-54222C63F5DA}x
0
1
y=-2x
2
2
0
-2
{5940675A-B579-460E-94D1-54222C63F5DA}x
0
y=-x-1
0
-1
-2
4
5
3
2
O
x
1
-1
-2
-1
y=-x+2
y=-2x
y=-????????x-1
?
(2)
讲授新课
1
2
y
3
4
5
-2
-3
4
5
3
2
O
x
1
-1
-2
-1
y=2x+3
y=3x
y=x-2
1
2
y
3
4
5
-2
-3
4
5
3
2
O
x
1
-1
-2
-1
y=-x+2
y=-2x
y=-????????x-1
?
1.观察上图(1)、(2),你有什么发现?
(1)
(2)
2.你能找出哪些因素影响了函数图像从左至右的变化趋势吗?
3.根据图像位置变化,你觉得应该怎样描述y随x的变化规律?
讲授新课
在一次函数y=kx+b中,
当k>0时,y的值随着x值的增大而增大;
当k<0时,y的值随着x值的增大而减小.
由此得到一次函数性质:
归纳总结
左
右
看图像要从____往____看.
????越大,倾斜程度就越大,????越小,倾斜程度就越小.
?
讲授新课
典例精析
【例1】 P1(x1,y1),P2(x2,y2)是一次函数y=-0.5x+3图象
上的两点,下列判断中,正确的是( )
A.y1>y2 C.当x1<x2时,y1<y2
B. y1<y2 D.当x1<x2时,y1>y2
D
解析:根据一次函数的性质: 当k<0时,y随x的增大而减小,所以D为正确答案.
提示:反过来也成立:当k<0时,y越大,x就越小.
讲授新课
练一练
1. 下列函数中:
(1) y=-3.5 x+4,(2) y=0.2x-5,(3)y=6x,(4) y=-????????x-3,(5) y=8x-7.
?
y的值随x增大而增大的函数是______________,图像是下降的函数是__________.
2. 在平面直角坐标系中,已知一次函数y=-2x+1的图像经过P1(x1,y1),P2(x2,y2)两点,若x1<x2,则y1 y2.(填“>”“<”或“=”)?
(2)、(3)、(5)
(1)、(4)
>
讲授新课
知识点二 观察一次函数的图象经过的象限
探究:画出直线
和 的图象,
并分析图象的特征.
-3
O
-2
2
3
1
2
3
-1
-1
-2
x
1
y
当k>0时,y随x的增大而增大,
这时函数的图象从左到右上升;
讲授新课
当k<0时,y随x的增大而_____,这时函数的图象从左到右_____.
-3
O
-2
2
3
1
2
3
-1
-1
-2
x
y
1
4
y减少
x增大
减小
下降
探究:画出直线 和 的图象,并分析图象的特征.
思考:k,b的值跟图象
有什么关系?
讲授新课
k 0,b 0
>
>
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
>
>
>
<
<
<
<
<
=
=
思考:根据一次函数的图象判断k,b的正负,并说出直线经过的象限:
讲授新课
归纳总结
一次函数y=kx+b中,k,b的正负对函数图象及性质有什么影响?
当k>0时,直线y=kx+b由左到右逐渐上升,y随x的增大而增大.
当k<0时,直线y=kx+b由左到右逐渐下降,y随x的增大而减小.
① b>0时,直线经过 第一、二、四象限;
② b<0时,直线经过第二、三、四象限.
① b>0时,直线经过第一、二、三象限;
② b<0时,直线经过第一、三、四象限.
讲授新课
典例精析
【例2】已知关于x的一次函数y=(2k-1)x+(2k+1).
(1)当k满足什么条件时,函数y的值随x的值的增大而增大?
(2)当k满足什么条件时,y=(2k-1)x+(2k+1)的图象经过原点?
当2k-1>0时,y的值随x的值增大而增大.
解2k-1>0,得k>0.5.
当2k+1=0,即k=-0.5时,
函数y=(2k-1)x+(2k+1)的图象经过原点.
讲授新课
练一练
1、两个一次函数y1=ax+b与y2=bx+a,它们在同一坐标系中的图象可能是( )
C
讲授新课
知识点三 一次函数的性质应用
【例3】某面食加工部每周用10000元流动资金采购面粉及其他物品,其中购买面粉的质量在1500kg-2000kg之间,面粉的单价为3.6元/千克,用剩余款额y元购买其他物品.设购买面粉的质量为x kg.
(1)求y与x的函数关系式,并写出自变量的取值范围.
解: (1)由题意,可知购买面粉的资金为3.6x元,总资金为10000元,即3.6x+y=10000,所以该函数关系式为:
y=-3.6x+10000,其中x的取值范围是1500≤x≤2000.
讲授新课
(2)求出购买其他物品的款额 y 的取值范围.
解:因为y=-3.6x+10000,k=-3.6<0,所以y的值随x的值的增大而减小.
因为1500≤x≤2000,
所以y的值最大为 -3.6×1500+10000=4600;
最小为 -3.6×2000+10000=2800.
故y的取值范围为2800≤y≤4600.
当堂检测
1. 当k<0时,一次函数y=kx-k的图像不经过 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
C
解:因为k<0,所以-k>0,
所以一次函数y=kx-k的图像经过第一、二、四象限.
2. 将直线y=2x-3向右平移3个单位长度,再向上平移1个单位长度,平移后所得直线的函数表达式为___________.
解:由题意可得y=2(x-3)-3+1,化简得y=2x-8
y=2x-8
当堂检测
3. 一次函数y=-x-2的大致图像为( )
D
A B C D
x
y
O
x
y
O
x
y
O
x
y
O
4. 在平面直角坐标系中,一次函数y=kx+b的图像如图所示,则k和b的取值范围是( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
C
x
y
O
当堂检测
5.下列四个选项中,关于一次函数y=x-2的图像或性质说法错误的是( )
A.y随x的增大而增大
B.经过第一、三、四象限
C.与x轴交于(-2,0)
D.与y轴交于(0,-2)
C
当堂检测
6. 一次函数y=2x-3的图像经过___________________.
第一、三、四象限
7. 已知一次函数y=kx-1,若y随x的增大而增大,则k的取值范围是_______.
k>0
8. 直线y=3x+1向下平移2个单位长度,所得直线的表达式是___________.
y=3x-1
当堂检测
9.已知一次函数y =(2k-1)x+3k+2.
(1)当k_____时,直线经过原点.
(4)当k______时,与 y 轴的交点在 x 轴的下方.
(3)当k______时,y 随 x 的增大而增大.
(5)当k_____时,它的图像经过二、三、四象限.
(2)当k______时,直线与 x 轴交于点(-1,0).
=?????????
?
=?????
?
>????????
?
<?????????
?
<?????????
?
<?????????
?
当堂检测
10、已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
解:(1)由题意得1-2m>0,解得 ;
(2)由题意得1-2m≠0且m-1<0,即 ;
(3)由题意得1-2m<0且m-1<0,解得 .
当堂检测
11.已知一次函数y= kx+b的图象平行于直线y= -3x,且经过点(2,-3).
(1)求这个一次函数的表达式;
(2)当y=6时,求x的值;
(3)在平面直角坐标系中画出这个一次函数的图象.
解:(1)∵一次函数y = kx+b 的图象平行于直线y = -3x.
∴k = -3,∴y = -3x+b.
把点(2,-3)的坐标代入y=-3x+b,得-3=-3x2+b,解得 b=3,
∴一次函数的表达式为y =-3x+3.
y =-3x+3
(2)当y=6时,-3x+3 =6,解得x=-1.
(3)如图所示.
课堂小结
一次函数函数的性质
当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
第3课时 一次函数的性质
数学(华东师大版)
八年级 下册
第17章 函数及其图象
学习目标
1、掌握一次函数的性质;
2、能灵活运用一次函数的图象与性质解答有关问题;
温故知新
1.一次函数图象有什么特点?
2.作出一次函数图象需要描出几个点?
只需要描出2个点.
一次函数y=kx+b的图象是一条直线,直线上所有点的坐标都满足表达式y=kx+b.
一般选直线与两坐标轴的两交点,即(0,b)和( ,0).
小试牛刀
在直角坐标系中,画出下列一次函数的图像.
(1) y=3x、y=2x、y=x
{5940675A-B579-460E-94D1-54222C63F5DA}x
0
1
y=3x
{5940675A-B579-460E-94D1-54222C63F5DA}x
0
1
y=2x
0
3
0
2
{5940675A-B579-460E-94D1-54222C63F5DA}x
0
0
y=x
0
1
1
2
y
3
4
5
-2
-3
4
5
3
2
O
x
1
-1
-2
-1
y=2x
y=3x
y=x
(2) y=-3x、y=-2x、y=-x
y=-3x
y=-2x
y=-x
你有什么发现?
讲授新课
知识点一 一次函数的性质
在直角坐标系中,画出下列一次函数的图像.
(1) y=2x+3、y=3x、y=x-2
{5940675A-B579-460E-94D1-54222C63F5DA}x
0
y=2x+3
0
{5940675A-B579-460E-94D1-54222C63F5DA}x
0
1
y=3x
3
-????????
?
0
3
{5940675A-B579-460E-94D1-54222C63F5DA}x
0
y=x-2
0
-2
2
1
2
y
3
4
5
-2
-3
4
5
3
2
O
x
1
-1
-2
-1
y=2x+3
y=3x
y=x-2
(1)
讲授新课
1
2
y
3
4
5
-2
-3
在直角坐标系中,画出下列一次函数的图像.
(2) y=-x+2、y=-2x、y=-????????x-1
?
{5940675A-B579-460E-94D1-54222C63F5DA}x
0
y=-x+2
0
{5940675A-B579-460E-94D1-54222C63F5DA}x
0
1
y=-2x
2
2
0
-2
{5940675A-B579-460E-94D1-54222C63F5DA}x
0
y=-x-1
0
-1
-2
4
5
3
2
O
x
1
-1
-2
-1
y=-x+2
y=-2x
y=-????????x-1
?
(2)
讲授新课
1
2
y
3
4
5
-2
-3
4
5
3
2
O
x
1
-1
-2
-1
y=2x+3
y=3x
y=x-2
1
2
y
3
4
5
-2
-3
4
5
3
2
O
x
1
-1
-2
-1
y=-x+2
y=-2x
y=-????????x-1
?
1.观察上图(1)、(2),你有什么发现?
(1)
(2)
2.你能找出哪些因素影响了函数图像从左至右的变化趋势吗?
3.根据图像位置变化,你觉得应该怎样描述y随x的变化规律?
讲授新课
在一次函数y=kx+b中,
当k>0时,y的值随着x值的增大而增大;
当k<0时,y的值随着x值的增大而减小.
由此得到一次函数性质:
归纳总结
左
右
看图像要从____往____看.
????越大,倾斜程度就越大,????越小,倾斜程度就越小.
?
讲授新课
典例精析
【例1】 P1(x1,y1),P2(x2,y2)是一次函数y=-0.5x+3图象
上的两点,下列判断中,正确的是( )
A.y1>y2 C.当x1<x2时,y1<y2
B. y1<y2 D.当x1<x2时,y1>y2
D
解析:根据一次函数的性质: 当k<0时,y随x的增大而减小,所以D为正确答案.
提示:反过来也成立:当k<0时,y越大,x就越小.
讲授新课
练一练
1. 下列函数中:
(1) y=-3.5 x+4,(2) y=0.2x-5,(3)y=6x,(4) y=-????????x-3,(5) y=8x-7.
?
y的值随x增大而增大的函数是______________,图像是下降的函数是__________.
2. 在平面直角坐标系中,已知一次函数y=-2x+1的图像经过P1(x1,y1),P2(x2,y2)两点,若x1<x2,则y1 y2.(填“>”“<”或“=”)?
(2)、(3)、(5)
(1)、(4)
>
讲授新课
知识点二 观察一次函数的图象经过的象限
探究:画出直线
和 的图象,
并分析图象的特征.
-3
O
-2
2
3
1
2
3
-1
-1
-2
x
1
y
当k>0时,y随x的增大而增大,
这时函数的图象从左到右上升;
讲授新课
当k<0时,y随x的增大而_____,这时函数的图象从左到右_____.
-3
O
-2
2
3
1
2
3
-1
-1
-2
x
y
1
4
y减少
x增大
减小
下降
探究:画出直线 和 的图象,并分析图象的特征.
思考:k,b的值跟图象
有什么关系?
讲授新课
k 0,b 0
>
>
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
>
>
>
<
<
<
<
<
=
=
思考:根据一次函数的图象判断k,b的正负,并说出直线经过的象限:
讲授新课
归纳总结
一次函数y=kx+b中,k,b的正负对函数图象及性质有什么影响?
当k>0时,直线y=kx+b由左到右逐渐上升,y随x的增大而增大.
当k<0时,直线y=kx+b由左到右逐渐下降,y随x的增大而减小.
① b>0时,直线经过 第一、二、四象限;
② b<0时,直线经过第二、三、四象限.
① b>0时,直线经过第一、二、三象限;
② b<0时,直线经过第一、三、四象限.
讲授新课
典例精析
【例2】已知关于x的一次函数y=(2k-1)x+(2k+1).
(1)当k满足什么条件时,函数y的值随x的值的增大而增大?
(2)当k满足什么条件时,y=(2k-1)x+(2k+1)的图象经过原点?
当2k-1>0时,y的值随x的值增大而增大.
解2k-1>0,得k>0.5.
当2k+1=0,即k=-0.5时,
函数y=(2k-1)x+(2k+1)的图象经过原点.
讲授新课
练一练
1、两个一次函数y1=ax+b与y2=bx+a,它们在同一坐标系中的图象可能是( )
C
讲授新课
知识点三 一次函数的性质应用
【例3】某面食加工部每周用10000元流动资金采购面粉及其他物品,其中购买面粉的质量在1500kg-2000kg之间,面粉的单价为3.6元/千克,用剩余款额y元购买其他物品.设购买面粉的质量为x kg.
(1)求y与x的函数关系式,并写出自变量的取值范围.
解: (1)由题意,可知购买面粉的资金为3.6x元,总资金为10000元,即3.6x+y=10000,所以该函数关系式为:
y=-3.6x+10000,其中x的取值范围是1500≤x≤2000.
讲授新课
(2)求出购买其他物品的款额 y 的取值范围.
解:因为y=-3.6x+10000,k=-3.6<0,所以y的值随x的值的增大而减小.
因为1500≤x≤2000,
所以y的值最大为 -3.6×1500+10000=4600;
最小为 -3.6×2000+10000=2800.
故y的取值范围为2800≤y≤4600.
当堂检测
1. 当k<0时,一次函数y=kx-k的图像不经过 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
C
解:因为k<0,所以-k>0,
所以一次函数y=kx-k的图像经过第一、二、四象限.
2. 将直线y=2x-3向右平移3个单位长度,再向上平移1个单位长度,平移后所得直线的函数表达式为___________.
解:由题意可得y=2(x-3)-3+1,化简得y=2x-8
y=2x-8
当堂检测
3. 一次函数y=-x-2的大致图像为( )
D
A B C D
x
y
O
x
y
O
x
y
O
x
y
O
4. 在平面直角坐标系中,一次函数y=kx+b的图像如图所示,则k和b的取值范围是( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
C
x
y
O
当堂检测
5.下列四个选项中,关于一次函数y=x-2的图像或性质说法错误的是( )
A.y随x的增大而增大
B.经过第一、三、四象限
C.与x轴交于(-2,0)
D.与y轴交于(0,-2)
C
当堂检测
6. 一次函数y=2x-3的图像经过___________________.
第一、三、四象限
7. 已知一次函数y=kx-1,若y随x的增大而增大,则k的取值范围是_______.
k>0
8. 直线y=3x+1向下平移2个单位长度,所得直线的表达式是___________.
y=3x-1
当堂检测
9.已知一次函数y =(2k-1)x+3k+2.
(1)当k_____时,直线经过原点.
(4)当k______时,与 y 轴的交点在 x 轴的下方.
(3)当k______时,y 随 x 的增大而增大.
(5)当k_____时,它的图像经过二、三、四象限.
(2)当k______时,直线与 x 轴交于点(-1,0).
=?????????
?
=?????
?
>????????
?
<?????????
?
<?????????
?
<?????????
?
当堂检测
10、已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
解:(1)由题意得1-2m>0,解得 ;
(2)由题意得1-2m≠0且m-1<0,即 ;
(3)由题意得1-2m<0且m-1<0,解得 .
当堂检测
11.已知一次函数y= kx+b的图象平行于直线y= -3x,且经过点(2,-3).
(1)求这个一次函数的表达式;
(2)当y=6时,求x的值;
(3)在平面直角坐标系中画出这个一次函数的图象.
解:(1)∵一次函数y = kx+b 的图象平行于直线y = -3x.
∴k = -3,∴y = -3x+b.
把点(2,-3)的坐标代入y=-3x+b,得-3=-3x2+b,解得 b=3,
∴一次函数的表达式为y =-3x+3.
y =-3x+3
(2)当y=6时,-3x+3 =6,解得x=-1.
(3)如图所示.
课堂小结
一次函数函数的性质
当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
