2023-2024学年数学湘教版七年级下册 4.5 垂线 第1课时 课件(共18张PPT)
文档属性
| 名称 | 2023-2024学年数学湘教版七年级下册 4.5 垂线 第1课时 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
第4章 相交线与平行线
4.5 垂线
第1课时
1.掌握垂直及相关概念;
2.能利用垂直的性质解决相关问题.
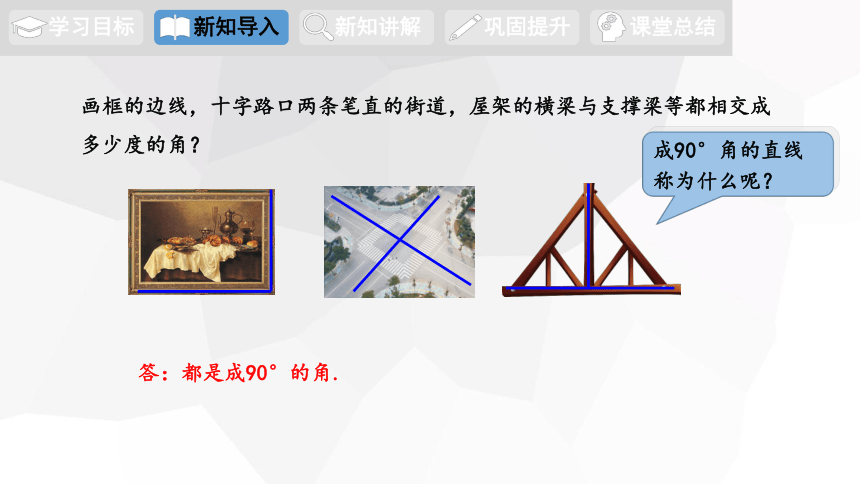
画框的边线,十字路口两条笔直的街道,屋架的横梁与支撑梁等都相交成多少度的角?
答:都是成90°的角.
成90°角的直线称为什么呢?
两条直线相交所成的四个角中,有一个是直角时(易知其余三个角也是直角),这两条直线叫做互相垂直,其中每一条直线叫做另一条的垂线,它们的交点叫做垂足.
O
1.垂直概念:
注意:
1.垂直是相交的特殊情况
2.判断两条直线互相垂直的关键是只要找到两条直线相交时,四个交角中有一个角是直角。
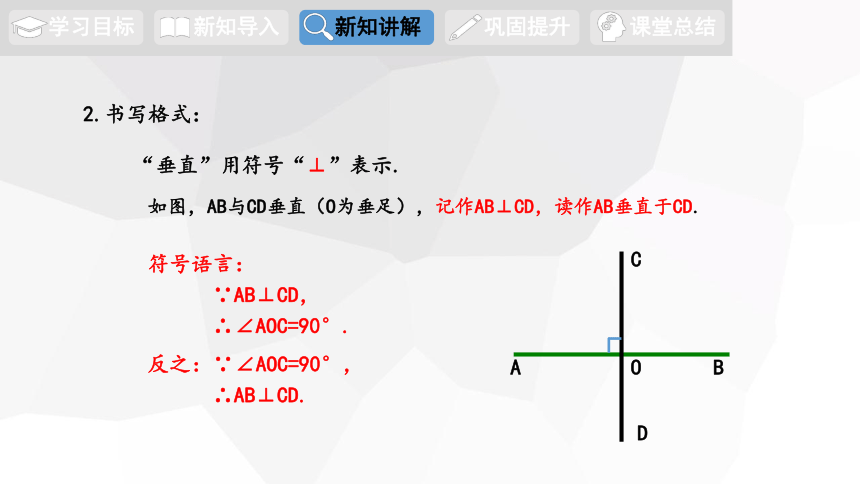
“垂直”用符号“⊥”表示.
如图,AB与CD垂直(O为垂足),记作AB⊥CD,读作AB垂直于CD.
2.书写格式:
符号语言:
∵AB⊥CD,
∴∠AOC=90°.
反之:∵∠AOC=90°,
∴AB⊥CD.
A
B
C
D
O
3.斜交(不垂直):
两条直线相交不成直角时,其中一条直线叫做另一条直线的斜线,它们的交点叫做斜足.
如图,直线CD是AB的斜线,同样,直线AB也是CD的斜线,点O是斜足.
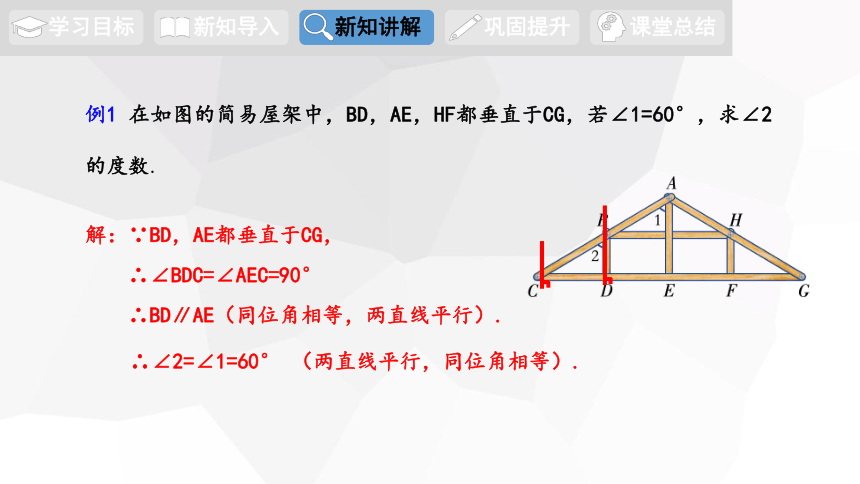
例1 在如图的简易屋架中,BD,AE,HF都垂直于CG,若∠1=60°,求∠2的度数.
解:∵BD,AE都垂直于CG,
∴BD∥AE(同位角相等,两直线平行).
∴∠2=∠1=60° (两直线平行,同位角相等).
∴∠BDC=∠AEC=90°
(1)如图,在同一平面内,如果a⊥l,b⊥l,那么a∥b吗?
∵a⊥l,b⊥l,
∴∠1=∠2=90°,
∴a∥b(同位角相等,两直线平行).
在同一平面内,垂直于同一条直线的两条直线平行.
(2)如图,在同一平面内,如果直线a∥b,l⊥a,那么l⊥b吗?
∵l⊥a,
∴∠1=90°.
∵a∥b,
∴∠2=∠1=90°(两直线平行,同位角相等)
∴l⊥b.
在同一平面内,如果一条直线垂直于两条平行线中的一条,那么这条直线垂直于另一条.
1.在同一个平面内,垂直于同一条直线的两条直线平行.
2. 在同一平面内,如果一条直线垂直于两条平行线中的一条,那么这条直线垂直于另一条.
例2 如图,已知CD⊥AB,∠1=∠2,求∠BEF的度数.
解:∵CD⊥AB,
∴CD∥EF(同位角相等,两直线平行).
又∵∠1=∠2,
∴∠BEF=∠BDC=90°(两直线平行,同位角相等).
∴∠BDC=90°
1.(1)两条直线垂直和相交是什么关系?
(2)能否认为在同一平面内,两条直线的位置关系有3种,为相交,平行,垂直?
垂直是相交的特殊情况
不能,平面内两条直线的位置有相交和平行两种关系.
(3)如何判定两条射线垂直?两条线段呢?
两条线段垂直、两条射线垂直、线段与射线垂直、线段与直线垂直、射线与直线垂直,都是指它们所在的直线垂直.
2.你能举出一些生活中与垂直有关的实例吗?
3.下列时刻中,时针与分针互相垂直的是( )
A.2点20分 B.3点整
C.12点10分 D.5点40分
解析: 在钟表的表面上,相邻数字(如1和2)与表中心连线的夹角为30°,而3点整时,时针指向3,分针指向12,故在3点整时时针与分针的夹角为直角.故选B
B
4.如图,直线AB,CD相交于O,EO⊥CD,∠BOE=60°,求∠AOC的度数.
解:∵EO⊥CD
∴∠EOD=90°,
又∠BOE=60°,
∴∠BOD=90°-∠BOE=30°.
∴∠AOC=∠BOD=30°(对顶角相等).
5.如图,DA⊥AB,CD⊥DA,∠B=56°,求∠C.
解:∵CD⊥DA,DA⊥AB,
∴AB∥CD(在同一平面内,垂直于同一条直线 的两条直线平行).
∴∠B+∠C=180°
(两直线平行,同旁内角互补).
又∵∠B=56°,
∴∠C=180°-56°=124°.
6.如图,∠ABC=90°,∠1=60°,过点B作AC的垂线BO,垂足是O,过点O作BC的垂线,垂足是D,若∠1=∠2,求∠ABO,∠BOD.
解:∵∠ABC=90°,∠1=60°,
∴∠ABO=30°.
∵BO⊥AC于O点,
∴∠BOC=90°,
又∵∠2=∠1,
∴∠BOD=∠ABO=30°.
垂线:
两条直线相交所成的四个角中,有一个是直角时(易知其余三个角也是直角),这两条直线叫做互相垂直,其中每一条直线叫做另一条的垂线,它们的交点叫做垂足.
“垂直”用符号“⊥”表示.
第4章 相交线与平行线
4.5 垂线
第1课时
1.掌握垂直及相关概念;
2.能利用垂直的性质解决相关问题.
画框的边线,十字路口两条笔直的街道,屋架的横梁与支撑梁等都相交成多少度的角?
答:都是成90°的角.
成90°角的直线称为什么呢?
两条直线相交所成的四个角中,有一个是直角时(易知其余三个角也是直角),这两条直线叫做互相垂直,其中每一条直线叫做另一条的垂线,它们的交点叫做垂足.
O
1.垂直概念:
注意:
1.垂直是相交的特殊情况
2.判断两条直线互相垂直的关键是只要找到两条直线相交时,四个交角中有一个角是直角。
“垂直”用符号“⊥”表示.
如图,AB与CD垂直(O为垂足),记作AB⊥CD,读作AB垂直于CD.
2.书写格式:
符号语言:
∵AB⊥CD,
∴∠AOC=90°.
反之:∵∠AOC=90°,
∴AB⊥CD.
A
B
C
D
O
3.斜交(不垂直):
两条直线相交不成直角时,其中一条直线叫做另一条直线的斜线,它们的交点叫做斜足.
如图,直线CD是AB的斜线,同样,直线AB也是CD的斜线,点O是斜足.
例1 在如图的简易屋架中,BD,AE,HF都垂直于CG,若∠1=60°,求∠2的度数.
解:∵BD,AE都垂直于CG,
∴BD∥AE(同位角相等,两直线平行).
∴∠2=∠1=60° (两直线平行,同位角相等).
∴∠BDC=∠AEC=90°
(1)如图,在同一平面内,如果a⊥l,b⊥l,那么a∥b吗?
∵a⊥l,b⊥l,
∴∠1=∠2=90°,
∴a∥b(同位角相等,两直线平行).
在同一平面内,垂直于同一条直线的两条直线平行.
(2)如图,在同一平面内,如果直线a∥b,l⊥a,那么l⊥b吗?
∵l⊥a,
∴∠1=90°.
∵a∥b,
∴∠2=∠1=90°(两直线平行,同位角相等)
∴l⊥b.
在同一平面内,如果一条直线垂直于两条平行线中的一条,那么这条直线垂直于另一条.
1.在同一个平面内,垂直于同一条直线的两条直线平行.
2. 在同一平面内,如果一条直线垂直于两条平行线中的一条,那么这条直线垂直于另一条.
例2 如图,已知CD⊥AB,∠1=∠2,求∠BEF的度数.
解:∵CD⊥AB,
∴CD∥EF(同位角相等,两直线平行).
又∵∠1=∠2,
∴∠BEF=∠BDC=90°(两直线平行,同位角相等).
∴∠BDC=90°
1.(1)两条直线垂直和相交是什么关系?
(2)能否认为在同一平面内,两条直线的位置关系有3种,为相交,平行,垂直?
垂直是相交的特殊情况
不能,平面内两条直线的位置有相交和平行两种关系.
(3)如何判定两条射线垂直?两条线段呢?
两条线段垂直、两条射线垂直、线段与射线垂直、线段与直线垂直、射线与直线垂直,都是指它们所在的直线垂直.
2.你能举出一些生活中与垂直有关的实例吗?
3.下列时刻中,时针与分针互相垂直的是( )
A.2点20分 B.3点整
C.12点10分 D.5点40分
解析: 在钟表的表面上,相邻数字(如1和2)与表中心连线的夹角为30°,而3点整时,时针指向3,分针指向12,故在3点整时时针与分针的夹角为直角.故选B
B
4.如图,直线AB,CD相交于O,EO⊥CD,∠BOE=60°,求∠AOC的度数.
解:∵EO⊥CD
∴∠EOD=90°,
又∠BOE=60°,
∴∠BOD=90°-∠BOE=30°.
∴∠AOC=∠BOD=30°(对顶角相等).
5.如图,DA⊥AB,CD⊥DA,∠B=56°,求∠C.
解:∵CD⊥DA,DA⊥AB,
∴AB∥CD(在同一平面内,垂直于同一条直线 的两条直线平行).
∴∠B+∠C=180°
(两直线平行,同旁内角互补).
又∵∠B=56°,
∴∠C=180°-56°=124°.
6.如图,∠ABC=90°,∠1=60°,过点B作AC的垂线BO,垂足是O,过点O作BC的垂线,垂足是D,若∠1=∠2,求∠ABO,∠BOD.
解:∵∠ABC=90°,∠1=60°,
∴∠ABO=30°.
∵BO⊥AC于O点,
∴∠BOC=90°,
又∵∠2=∠1,
∴∠BOD=∠ABO=30°.
垂线:
两条直线相交所成的四个角中,有一个是直角时(易知其余三个角也是直角),这两条直线叫做互相垂直,其中每一条直线叫做另一条的垂线,它们的交点叫做垂足.
“垂直”用符号“⊥”表示.
