2023-2024学年数学湘教版七年级下册 6.1.1 平均数 第1课时 课件(共16张PPT)
文档属性
| 名称 | 2023-2024学年数学湘教版七年级下册 6.1.1 平均数 第1课时 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 08:59:01 | ||
图片预览





文档简介
(共16张PPT)
第6章 数据的分析
6.1.1 平均数
第1课时
1.理解算术平均数的概念,掌握算数平均数的计算方法;
2.能利用算术平均数的作用与特点解决相关问题.
78是83 、78、65、99、54、89的算术平均数.
问题1 不久前同学们进行了期中考试,随机抽取了班中6名同学的分数,分别为:83 、78、65、99、54、89,那这6名同学的平均分是多少呢?
在小学阶段,我们对平均数有过一些了解,知道平均数是对数据进行分析的一个重要指标.
=78
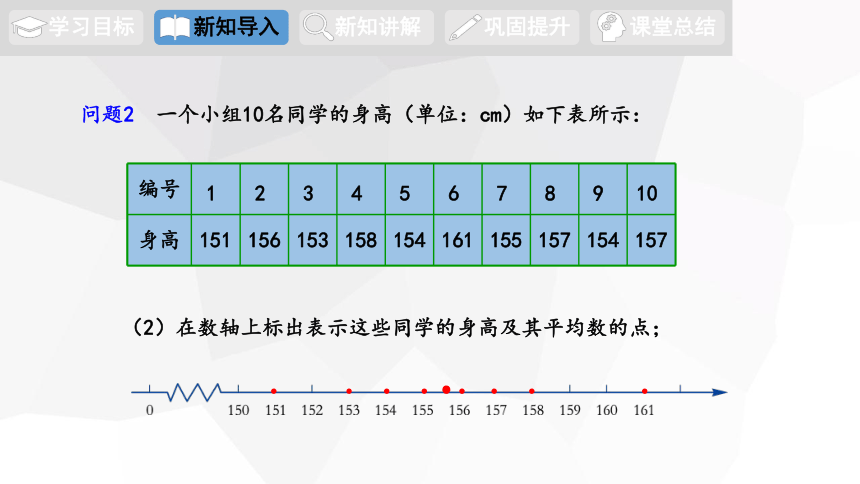
问题2 一个小组10名同学的身高(单位:cm)如下表所示:
编号
身高 151 156 153 158 154 161 155 157 154 157
1
2
3
4
5
6
7
8
9
10
(1)计算10名同学身高的平均数;
平均数:
=155.6(cm).
=(151+156+153+158+154+161+155+157+154+157)÷10
问题2 一个小组10名同学的身高(单位:cm)如下表所示:
编号
身高 151 156 153 158 154 161 155 157 154 157
1
2
3
4
5
6
7
8
9
10
(2)在数轴上标出表示这些同学的身高及其平均数的点;
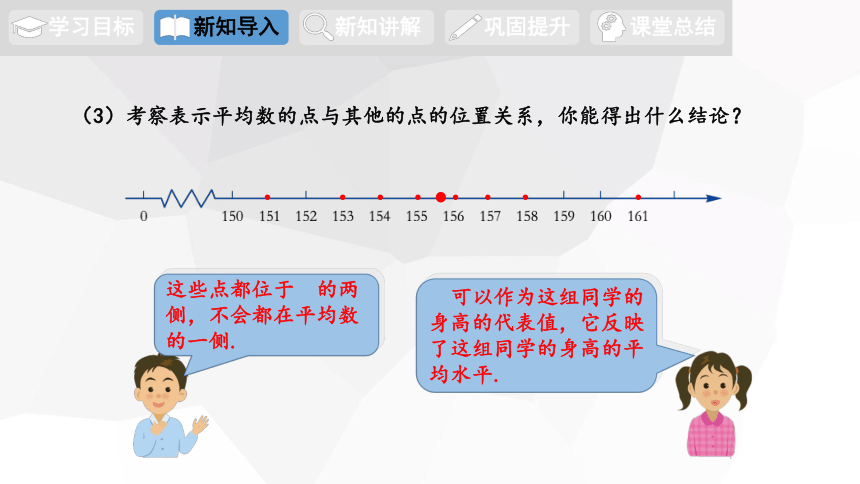
(3)考察表示平均数的点与其他的点的位置关系,你能得出什么结论?
这些点都位于 的两侧,不会都在平均数的一侧.
可以作为这组同学的身高的代表值,它反映了这组同学的身高的平均水平.
平均数的大小与一组数据的每个数据都有关系,如果这组数据中的一个数据变大,其平均数将变大;若这组数据中的一个数据变小,平均数将变小.
2.平均数的作用和特点:
1. 平均数与数据组的关系是:
平均数是一组数据的数值大小的集中代表值,它刻画了这组数据整体的平均状态,体现了这组数据的整体性质,对于这组数据的个体性质不能作出什么结论.
例题 某农业技术员试种了三个品种的棉花各10株.秋收时他清点了这30株棉花的结桃数如下表:
棉花品种 结桃数(个)
甲 84,79,81,84,85,82,83,86,87,81
乙 85,84,89,79,81,91,79,76,82,84
丙 83,85,87,78,80,75,82,83,81,86
哪个品种较好?
分析:平均数可以作为一组数据的代表值,它刻画了这组数据的平均水平.当我们要比较棉花的品种时,可以计算出这些棉花结桃数的平均数,再通过平均数来进行比较.
解:设甲、乙、丙三个品种的平均结桃数分别为 则
棉花品种 结桃数(个)
甲 84,79,81,84,85,82,83,86,87,81
乙 85,84,89,79,81,91,79,76,82,84
丙 83,85,87,78,80,75,82,83,81,86
由于甲种棉花的平均结桃数最高,所以我们可以认为甲种棉花较好.
计算器一般有统计功能,我们可以利用该功能求一组数据的平均数. 不同型号的计算器其操作步骤(按键)可能不同,操作时需参阅计算器的说明书.
通常先按统计键,使计算器进入统计运算模式,然后依次输入数据x1, ,x2, ,…,最后按求平均数的功能键,即可得到该组数据的平均数。
在一次全校歌咏比赛中,7位评委给一个班级的打分分别是:9.00,8.00,9.10,9.10,9.15,9.00,9.58.怎样评分比较公正?
我们可以计算该班级歌咏比赛的平均分:
这个分数才比较合理地反映了这个班级的最后得分.
去掉一个最高分和一个最低分后班级歌咏比赛的平均分:
但实际上评委的评判受主观因素影响比较大,评分也比较悬殊,为了消除极端数对平均数的影响,一般去掉一个最高分和一个最低分.
编号
初赛 90 85 85 78 101 105 97 96
复赛 100 90 86 78 98 100 106 98
1
2
3
4
5
6
7
8
(1)计算这组同学初赛和复赛的平均成绩。
答:这组同学初赛的平均成绩为92.125,复赛的平均成绩为94.5.
(2)你认为这组同学的初赛成绩好,还是复赛成绩好?
答:复赛的成绩好.
1.七年级(1)班举行1min跳绳比赛,以小组为单位参赛.第1小组有8名同学,他们初赛和复赛时的成绩如下表(单位:次):
2.某跳水队计划招收一批新运动员.请6位评委给选拔赛参加者打分,平均分数超过8.5分才能被选上.刘明在比赛时的成绩为8.30,8.25,8.45,8.20,8.30,9.60,你认为刘明选得上吗?
答:刘明的平均分数为8.52,所以刘明能被选上.
刘明平均数= =8.52
3.小明班上同学的平均身高是1.4m,小强班上同学的平均身高是1.45m.小明一定比小强矮吗?
答:因为平均值容易受个别特殊数据的影响.所以小明不一定比小强矮.
4. 有10个机器零件,测得质量分别如下:(单位:g)
22.5,22.7,22.8,22.7,22.5
22.9,23.0,23.4,23.2,23.3
试计算机器零件质量的平均数.
答:机器零件质量的平均数为22.9 .
零件质量平均数=
=22.9
算术平均数
3.算术平均数的意义:作为一组数据的一个代表值,反映一组数据的平均水平.
( ).
2.算术平均数的表示方法:
1.一般地,若n个数x1,x2,…,xn,则
叫做这n个数的算术平
均数,记作“
”,读作“x拔”.
第6章 数据的分析
6.1.1 平均数
第1课时
1.理解算术平均数的概念,掌握算数平均数的计算方法;
2.能利用算术平均数的作用与特点解决相关问题.
78是83 、78、65、99、54、89的算术平均数.
问题1 不久前同学们进行了期中考试,随机抽取了班中6名同学的分数,分别为:83 、78、65、99、54、89,那这6名同学的平均分是多少呢?
在小学阶段,我们对平均数有过一些了解,知道平均数是对数据进行分析的一个重要指标.
=78
问题2 一个小组10名同学的身高(单位:cm)如下表所示:
编号
身高 151 156 153 158 154 161 155 157 154 157
1
2
3
4
5
6
7
8
9
10
(1)计算10名同学身高的平均数;
平均数:
=155.6(cm).
=(151+156+153+158+154+161+155+157+154+157)÷10
问题2 一个小组10名同学的身高(单位:cm)如下表所示:
编号
身高 151 156 153 158 154 161 155 157 154 157
1
2
3
4
5
6
7
8
9
10
(2)在数轴上标出表示这些同学的身高及其平均数的点;
(3)考察表示平均数的点与其他的点的位置关系,你能得出什么结论?
这些点都位于 的两侧,不会都在平均数的一侧.
可以作为这组同学的身高的代表值,它反映了这组同学的身高的平均水平.
平均数的大小与一组数据的每个数据都有关系,如果这组数据中的一个数据变大,其平均数将变大;若这组数据中的一个数据变小,平均数将变小.
2.平均数的作用和特点:
1. 平均数与数据组的关系是:
平均数是一组数据的数值大小的集中代表值,它刻画了这组数据整体的平均状态,体现了这组数据的整体性质,对于这组数据的个体性质不能作出什么结论.
例题 某农业技术员试种了三个品种的棉花各10株.秋收时他清点了这30株棉花的结桃数如下表:
棉花品种 结桃数(个)
甲 84,79,81,84,85,82,83,86,87,81
乙 85,84,89,79,81,91,79,76,82,84
丙 83,85,87,78,80,75,82,83,81,86
哪个品种较好?
分析:平均数可以作为一组数据的代表值,它刻画了这组数据的平均水平.当我们要比较棉花的品种时,可以计算出这些棉花结桃数的平均数,再通过平均数来进行比较.
解:设甲、乙、丙三个品种的平均结桃数分别为 则
棉花品种 结桃数(个)
甲 84,79,81,84,85,82,83,86,87,81
乙 85,84,89,79,81,91,79,76,82,84
丙 83,85,87,78,80,75,82,83,81,86
由于甲种棉花的平均结桃数最高,所以我们可以认为甲种棉花较好.
计算器一般有统计功能,我们可以利用该功能求一组数据的平均数. 不同型号的计算器其操作步骤(按键)可能不同,操作时需参阅计算器的说明书.
通常先按统计键,使计算器进入统计运算模式,然后依次输入数据x1, ,x2, ,…,最后按求平均数的功能键,即可得到该组数据的平均数。
在一次全校歌咏比赛中,7位评委给一个班级的打分分别是:9.00,8.00,9.10,9.10,9.15,9.00,9.58.怎样评分比较公正?
我们可以计算该班级歌咏比赛的平均分:
这个分数才比较合理地反映了这个班级的最后得分.
去掉一个最高分和一个最低分后班级歌咏比赛的平均分:
但实际上评委的评判受主观因素影响比较大,评分也比较悬殊,为了消除极端数对平均数的影响,一般去掉一个最高分和一个最低分.
编号
初赛 90 85 85 78 101 105 97 96
复赛 100 90 86 78 98 100 106 98
1
2
3
4
5
6
7
8
(1)计算这组同学初赛和复赛的平均成绩。
答:这组同学初赛的平均成绩为92.125,复赛的平均成绩为94.5.
(2)你认为这组同学的初赛成绩好,还是复赛成绩好?
答:复赛的成绩好.
1.七年级(1)班举行1min跳绳比赛,以小组为单位参赛.第1小组有8名同学,他们初赛和复赛时的成绩如下表(单位:次):
2.某跳水队计划招收一批新运动员.请6位评委给选拔赛参加者打分,平均分数超过8.5分才能被选上.刘明在比赛时的成绩为8.30,8.25,8.45,8.20,8.30,9.60,你认为刘明选得上吗?
答:刘明的平均分数为8.52,所以刘明能被选上.
刘明平均数= =8.52
3.小明班上同学的平均身高是1.4m,小强班上同学的平均身高是1.45m.小明一定比小强矮吗?
答:因为平均值容易受个别特殊数据的影响.所以小明不一定比小强矮.
4. 有10个机器零件,测得质量分别如下:(单位:g)
22.5,22.7,22.8,22.7,22.5
22.9,23.0,23.4,23.2,23.3
试计算机器零件质量的平均数.
答:机器零件质量的平均数为22.9 .
零件质量平均数=
=22.9
算术平均数
3.算术平均数的意义:作为一组数据的一个代表值,反映一组数据的平均水平.
( ).
2.算术平均数的表示方法:
1.一般地,若n个数x1,x2,…,xn,则
叫做这n个数的算术平
均数,记作“
”,读作“x拔”.
