北师大版九年级数学上册第四章 图形的相似 单元复习题(含解析)
文档属性
| 名称 | 北师大版九年级数学上册第四章 图形的相似 单元复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 757.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 09:16:32 | ||
图片预览



文档简介
北师大版九年级数学上册第四章图形的相似单元复习题
一、选择题
1.若,则的值为( )
A.1 B. C. D.
2.如图,在 中, , , , ,则 的长为( )
A. B. C. D.
3.下列图形中 定相似的是( )
A.直角三角形都相似 B.等腰三角形都相似
C.矩形都相似 D.等腰直角三角形都相似
4.已知点P是线段AB的黄金分割点(AP>PB),AB=4,那么AP的长是( )
A. B. C. D.
5.如图,中,点D,E分别在边上.若,,则的长为( )
A. B. C. D.3
6.如图,在矩形ABCD中,M和N分别为AB和CD的中点,如果矩形ABCD∽矩形MNCB,那么他们的相似比为( )
A. B. C.2:1 D.1:1
7.如图,在中,.将沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B.
C. D.
8.如图,小明在A时测得某树的影长为,B时又测得该树的影长为,若两次日照的光线互相垂直,则树的高度为( )
A. B. C. D.
9.如图,在灯光的正下方,它在地面上形成的影子是,平行于地面,且到的距离和与地面的距离相等,已知在中,,下面关于的说法,其中正确的是( )
A.的面积为 B.的周长为
C. D.
10.如图,在△ABC纸板中,AC=4,BC=8,AB=10,P是BC上一点,沿过点P的直线剪下一个与△ABC相似的小三角形纸板.针对CP的不同取值,三人的说法如下.下列判断正确的是( )
甲:若CP=4,则有3种不同的剪法;乙:若CP=2,则有4种不同的剪法;
丙:若CP=1,则有3种不同的剪法.
A.只有甲错 B.只有乙错
C.只有丙错 D.甲、乙、丙都对
二、填空题
11.若,且,则 .
12.如图,,直线,与这三条平行线分别交于点A,C,E,和点B,D,F.已知,则的长为 .
13.如图,在 中, , , , ,垂足为 , 为 的中点, 与 交于点 ,则 的长为 .
14.同学们学习了线段的黄金分割之后,曾老师提出了一个新的定义:点C是线段AB上一点,若=kn,则称点C为线段AB的“近A,n阶黄金分割点”.例如:若=k2,则称点C为线段AB的“近A,2阶黄金分割点”;若=k3,则称点C为线段AB的“近A,3阶黄金分割点”.若点C为线段AB的“近A,6阶黄金分割点”时,k6= .
三、解答题
15.已知,,是的三边长,且.
(1)求的值;
(2)若的周长为81,求三边,,的长.
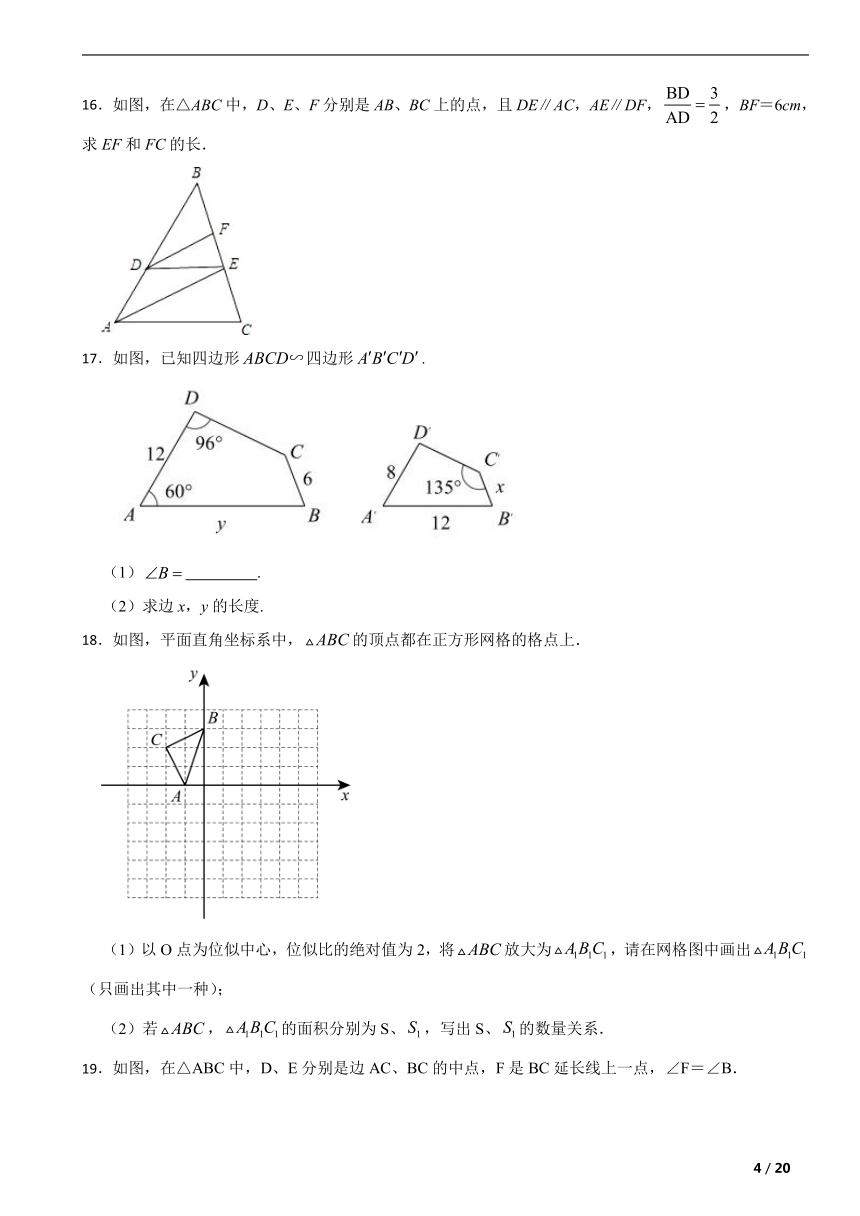
16.如图,在△ABC中,D、E、F分别是AB、BC上的点,且DE∥AC,AE∥DF,,BF=6cm,求EF和FC的长.
17.如图,已知四边形四边形.
(1) .
(2)求边x,y的长度.
18.如图,平面直角坐标系中,的顶点都在正方形网格的格点上.
(1)以O点为位似中心,位似比的绝对值为2,将放大为,请在网格图中画出(只画出其中一种);
(2)若,的面积分别为S、,写出S、的数量关系.
19.如图,在△ABC中,D、E分别是边AC、BC的中点,F是BC延长线上一点,∠F=∠B.
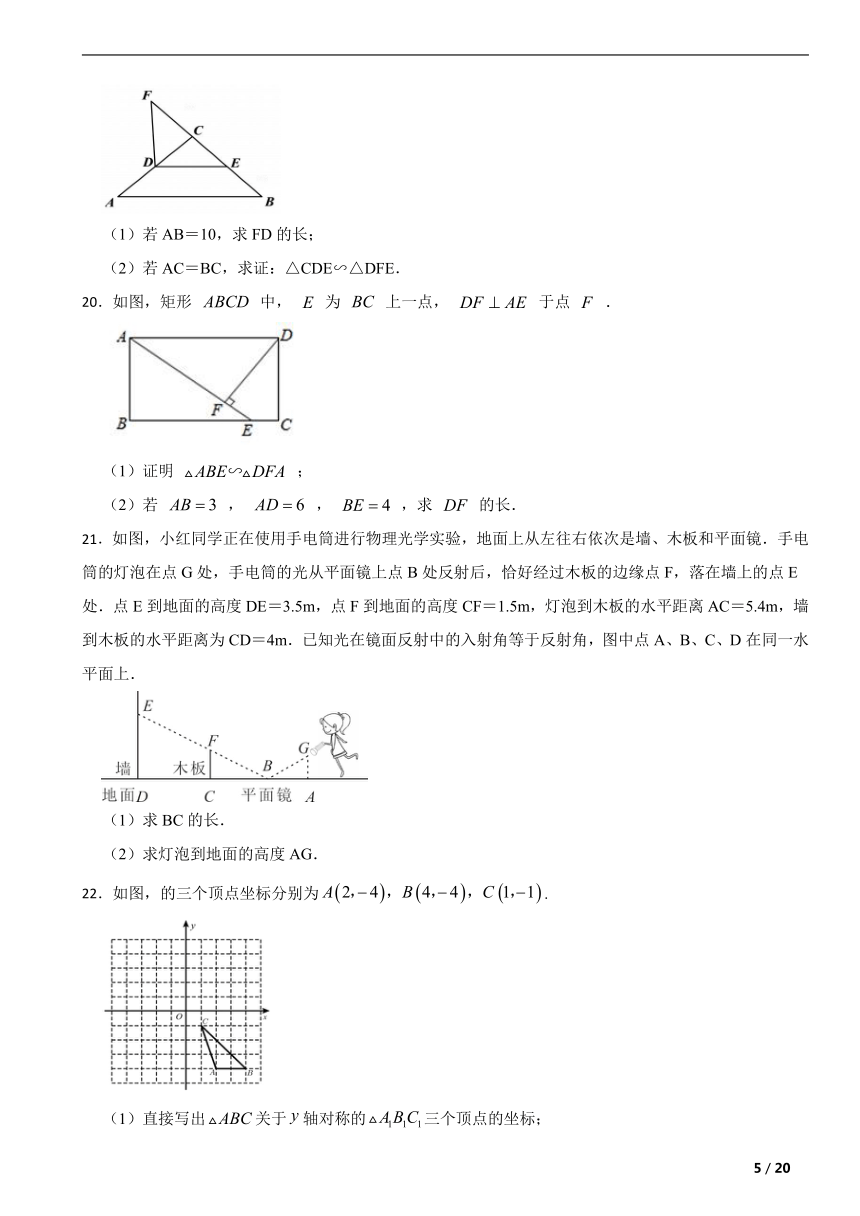
(1)若AB=10,求FD的长;
(2)若AC=BC,求证:△CDE∽△DFE.
20.如图,矩形 中, 为 上一点, 于点 .
(1)证明 ;
(2)若 , , ,求 的长.
21.如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡在点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度DE=3.5m,点F到地面的高度CF=1.5m,灯泡到木板的水平距离AC=5.4m,墙到木板的水平距离为CD=4m.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上.
(1)求BC的长.
(2)求灯泡到地面的高度AG.
22.如图,的三个顶点坐标分别为.
(1)直接写出关于轴对称的三个顶点的坐标;
(2)画出绕点逆时针旋转后的;
(3)以点为位似中心,在网格中画出的位似图形,使与的相似比为.
23.综合问题:从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,DC= - ,BD= ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求CB长.
答案解析部分
1.【答案】B
2.【答案】C
【解析】【解答】解:∵ ,
∴ ,即 ,
∴ .
故答案为:C.
【分析】根据平行线分线段成比例定理“两条直线被一组平行线所截,截得的对应线段的长度成比例”可得比例式求解.
3.【答案】D
【解析】【解答】解:A、两个直角三角形的边不一定成比例,角不一定相等,不一定相似,故本选项不符合题意;
B、两个等腰三角形的边不一定成比例,角不一定相等,不一定相似,故本选项不符合题意;
C、两个矩形的对应角相等,但对应边不一定成比例,不一定相似,故本选项不符合题意;
D、两个等腰直角三角形的对应边一定成比例,对应角一定相等,所以一定相似,故本选项符合题意.
故答案为:D.
【分析】根据相似图形的对应边成比例,对应角相等,结合直角三角形、等腰三角形、矩形以及等腰直角三角形的特点对各选项进行分析判断.
4.【答案】A
【解析】【解答】根据黄金比的定义得: ,得 .
故答案为:A.
【分析】先求出,再根据AB=4计算求解即可。
5.【答案】C
【解析】【解答】解:∵
又∵∠DAE=∠CAB
∴△DAE∽△CAB
∴
∴DE=BC==
故答案为:C.
【分析】由两边对应成比例且夹角相等的两个三角形相似,可得△DAE∽△CAB,相似三角形的对应边之比等于相似比得,从而代入可算出DE的长.
6.【答案】A
【解析】【解答】解:∵M和N分别为AB和CD的中点,
∴矩形ABCD的面积是矩形MNCB的面积的2倍,
∵果矩形ABCD∽矩形MNCB
∴矩形ABCD与矩形MNCB的相似比为 .
故答案为:A.
【分析】根据相似多边形的性质,面积的比是相似比的平方,即可得解.
7.【答案】A
【解析】【解答】解:
A:没有能判定相似的条件,故不相似,不符合题意;
B:两角相等,故相似,符合题意;
C:两边对应成比例且夹角相等,故相似,符合题意;
D:两角相等,故相似,符合题意;
故答案为:A.
【分析】利用相似三角形的判定条件进行逐一判断即可求解.
8.【答案】B
【解析】【解答】解:根据题意,作△EFC,树高为CD,且∠ECF=90°,ED=2m,FD=8m;
∵∠E+∠F=90°,∠E+∠ECD=90°,
∴∠ECD=∠F,
又
∴△EDC∽△CDF,
∴,即DC2=ED FD=2×8=16,
解得CD=4m(负值舍去).
故答案为:B.
【分析】如图,证明△EDC∽△CDF,利用相似三角形对应边成比例即可求解.
9.【答案】B
【解析】【解答】解:由题意可知:
AB,
所以,,
所以且相似比为2:1,
因为,
所以,故A选项错误,不符合题意;
因为,
所以,故B选项正确,符合题意;
因为,
所以故C、D选项错误,不符合题意;
故选:B.
【分析】分别求出AB=、、,再依据相似三角形的性质进行判断即可.
10.【答案】C
【解析】【解答】解:如图,过P作交AB于D,作交AC于E,则,;
过P作,交AB于F,则,此时,;
过P作,交AC于F,则,此时,,;
当时,有4种不同的剪法;当时,有3种不同的剪法,甲和乙对,丙错 .
故答案为:C.
【分析】根据相似三角形的对应边成比例,得到的长的取值范围.
11.【答案】6
【解析】【解答】设,
∴a=6k,b=5k,c=4k,
∵,
∴6k+5k-8k=3,
解得:k=1,
∴a=6×1=6,
故答案为:6.
【分析】设,可得a=6k,b=5k,c=4k,再结合求出k的值,最后求出a的值即可.
12.【答案】2
13.【答案】
【解析】【解答】如解图,过点 作 于 ,
∵ ,
∴ ,
∴ ,
∵ ,点 是 的中点,
∴ ,
∵ ,
∴ ∽
∴
∴ ,
设 为 ,则 ,由勾股定理得 ,
又∵ ,
∴ ,
则 ,
∵ 且 ,
∴ ∽ ,
∴ ,
即 ,
解得 ,
∴ .
∵
∴
∴
∴
故答案为:
【分析】过点 作 于 ,根据 ∽ 可得出AH,FH的关系式,然后根据 ∽ ,可得 ,构建方程即可求解即可。
14.【答案】
【解析】【解答】解:由题意,点C为线段AB的“近A,6阶黄金分割点”时,,
∴,
∵,
∴,
∵,
∴,
即:,
整理得:,
解得:或,
经检验,或是上述分式方程的解,
∵,
∴,
故答案为:.
【分析】由题意得,则,再由=,即得,整理得,再解方程即可.
15.【答案】(1)解:因为,
设,则,
(2)解:令,得
所以,,.
【解析】【分析】(1)利用设k法可得:设,则, ,再将其代入计算即可;
(2)将,,代入求出k的值,再求出a、b、c的值即可.
16.【答案】解:∵AE∥DF,
∴,即,
∴EF=4,
∴BE=BF+EF=6+4=10,
∵DE∥AC,
∴,即 ,
∴CE=,
∴CF=CE+EF=.
【解析】【分析】先根据平行线分线段成比例即可得到EF,进而即可得到BE,再根据平行线分线段成比例即可得到CE,进而即可求解。
17.【答案】(1)
(2)解:∵四边形四边形,
∴
解得,.
【解析】【解答】解:(1)∵已知四边形四边形
∴∠C=∠C'=135°
∴
故答案为:
【分析】(1)根据相似图形性质可得∠C=∠C'=135°,再根据四边形内角和定理即可求出答案.
(2)根据相似图形的相似比性质即可求出答案.
18.【答案】(1)解:如图所示:即为所求;(另一种同样给分)
(2)解:∵,位似比的绝对值为2,放大为,
∴和相似比为,
∴
即:.
【解析】【分析】(1)利用位似图形的性质求得A、B、C对应点A1B1C1的位置,连接即可求解;
(2)利用位似图形的性质:面积比等于相似比的平方,代入数据即可求解.
19.【答案】(1)解:∵D、E分别是AC、BC的中点,
∴DE//AB, DE=AB=5
又∵DE//AB,
∴∠DEC= ∠B.
而∠ F= ∠ B,
∴∠DEC =∠B,
∴FD=DE=5
(2)解:∵AC=BC,
∴∠A=∠B.
又∠CDE=∠A,∠CED= ∠B,
∴∠CDE=∠B.
而∠B=∠F,
∴∠CDE=∠F,∠CED=∠DEF,
∴△CDE∽△DFE .
【解析】【分析】(1)根据平行线的性质可得∠DEC= ∠B,再结合∠F= ∠B,可得∠DEC =∠B,最后利用等角对等边的性质可得FD=DE=5;
(2)证明∠CDE=∠F,∠CED=∠DEF,即可证明△CDE∽△DFE。
20.【答案】(1)证明:∵四边形 是矩形,
∴ , ,
∴ ,
∵ ,
∴ ,
在 和 中, ,
∴ ;
(2)解:∵在 中, , ,
,
由(1)已证: ,
∴ ,即 ,
解得 .
【解析】【分析】(1)根据四边形 是矩形,得出 , ,再根据垂直的定义得出 ,利用全等三角形的性质得出 ;
(2)在 中, , ,利用勾股定理得出AE的值,由(1)已证: ,得出 ,解得即可。
21.【答案】(1)解:由题意可得:FC∥DE,
则△BFC∽△BED,
故,
即,
解得:BC=3,
经检验,BC=3是上述分式方程的解,
∴BC的长为3m;
(2)解:∵AC=5.4m,
∴AB=5.4-3=2.4(m),
∵光在镜面反射中的入射角等于反射角,
∴∠FBC=∠GBA,
又∵∠FCB=∠GAB,
∴△BGA∽△BFC,
∴,
∴,
解得:AG=1.2(m),
∴灯泡到地面的高度AG为1.2m.
【解析】【分析】(1)先证明△BFC∽△BED,可得,将数据代入可得,再求出BC的长即可;
(2)先证明△BGA∽△BFC,可得,将数据代入可得,再求出AG的长即可。
22.【答案】(1)解:
(2)解:绕点逆时针旋转,如图所示,
即为所求图形的位置.
(3)解:∵,,,点为位似中心,相似比为,即位似比为,
∴,,,
∴延长到,使得,即,延长到,使得,即,连接,,得;
反向延长到,使得,即,反向延长到,使得,即,连接,,得,如图所示,
∴点为位似中心,相似比为,,都是所求图形.
【解析】【解答】解:(1)关于轴对称的三个顶点的坐标,横坐标变为原来的相反数,纵坐标不变,,
∴.
【分析】(1)关于y轴对称的点:横坐标互为相反数,纵坐标相同,据此不难得到点A1、B1、C1的坐标;
(2)根据旋转的性质,分别将点A、B、C绕点O逆时针旋转90°得到点A2、B2、C2,然后顺次连接即可;
(3)分别延长AB、CB,或反向延长BA、BC,使A3B=2AB,C3B=2CB,然后顺次连接即可.
23.【答案】(1)证明:∵∠ A=40°,∠ B=60°,
∴ ∠ACB=180°-∠A-∠B=80°,
∵∠A ∠B ∠ACB,∴ △ABC不是等腰三角形.
∵CD平分∠ ACB,∴ ∠ACD=∠BCD= ∠ACB=40°,
∴ ∠ACD=∠ A=40°,∴ △ACD为等腰三角形.∴ ∠DCB=∠ A=40°,
∠CBD=∠ ABC, ∴ △BCD∽△BAC,∴ CD是△ABC的完美分割线.
(2)解:①如图3所示,
当AD=CD时,∠ACD=∠ A=48°,根据完美分割线的定义,可得△BDC∽△BCA,∴∠BCD=∠A=48°,则∠ACB=∠ACD+∠BCD=96°.
②如图4所示,
当AD=AC时,∠ACD=∠ ADC= ,
根据完美分割线的定义,可得△BDC∽△BCA,∴∠BCD=∠A=48°,
∴∠ACB=∠ACD+∠BCD=114°.
③如图5所示,
当AC=CD时,∠ADC=∠ A=48°.∵△BDC∽△BCA,∴∠BCD=∠A=48°,根据完美分割线的定义,可得△BDC∽△BCA,∴∠BCD=∠A=48°,
∴这与∠ADC>∠BCD矛盾,所以图5的情况不符合题意.
综上所述,∠ACB的度数为96°或114°.
(3)解:∵△ACD是以CD为底边的等腰三角形,AC=2,∴AC=AD=2.
∵△BCD∽△BAC,∴
,解得BC=
写成:BC= 或者BC= ,所有结果没化简均不扣分
【解析】【分析】(1)首先由三角形内角和定理求出∠ACB的度数,然后根据∠A、∠B、∠ACB的度数的关系即可判断出△ABC是否为等腰三角形,由角平分线的定义求出∠ACD、∠BCD的度数,然后根据相似三角形的判定定理解答即可;
(2)分①AD=CD,②AD=AC,③AC=CD三种情况, 根据完美分割线的定义,可得△BDC∽△BCA, 由相似三角形的性质可得∠BCD=∠A,最后由角的和差关系求解即可;
(3)首先由等腰三角形的性质可得AC=AD=2,然后由相似三角形对应边成比例就可求出BC的值.
1 / 1
一、选择题
1.若,则的值为( )
A.1 B. C. D.
2.如图,在 中, , , , ,则 的长为( )
A. B. C. D.
3.下列图形中 定相似的是( )
A.直角三角形都相似 B.等腰三角形都相似
C.矩形都相似 D.等腰直角三角形都相似
4.已知点P是线段AB的黄金分割点(AP>PB),AB=4,那么AP的长是( )
A. B. C. D.
5.如图,中,点D,E分别在边上.若,,则的长为( )
A. B. C. D.3
6.如图,在矩形ABCD中,M和N分别为AB和CD的中点,如果矩形ABCD∽矩形MNCB,那么他们的相似比为( )
A. B. C.2:1 D.1:1
7.如图,在中,.将沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B.
C. D.
8.如图,小明在A时测得某树的影长为,B时又测得该树的影长为,若两次日照的光线互相垂直,则树的高度为( )
A. B. C. D.
9.如图,在灯光的正下方,它在地面上形成的影子是,平行于地面,且到的距离和与地面的距离相等,已知在中,,下面关于的说法,其中正确的是( )
A.的面积为 B.的周长为
C. D.
10.如图,在△ABC纸板中,AC=4,BC=8,AB=10,P是BC上一点,沿过点P的直线剪下一个与△ABC相似的小三角形纸板.针对CP的不同取值,三人的说法如下.下列判断正确的是( )
甲:若CP=4,则有3种不同的剪法;乙:若CP=2,则有4种不同的剪法;
丙:若CP=1,则有3种不同的剪法.
A.只有甲错 B.只有乙错
C.只有丙错 D.甲、乙、丙都对
二、填空题
11.若,且,则 .
12.如图,,直线,与这三条平行线分别交于点A,C,E,和点B,D,F.已知,则的长为 .
13.如图,在 中, , , , ,垂足为 , 为 的中点, 与 交于点 ,则 的长为 .
14.同学们学习了线段的黄金分割之后,曾老师提出了一个新的定义:点C是线段AB上一点,若=kn,则称点C为线段AB的“近A,n阶黄金分割点”.例如:若=k2,则称点C为线段AB的“近A,2阶黄金分割点”;若=k3,则称点C为线段AB的“近A,3阶黄金分割点”.若点C为线段AB的“近A,6阶黄金分割点”时,k6= .
三、解答题
15.已知,,是的三边长,且.
(1)求的值;
(2)若的周长为81,求三边,,的长.
16.如图,在△ABC中,D、E、F分别是AB、BC上的点,且DE∥AC,AE∥DF,,BF=6cm,求EF和FC的长.
17.如图,已知四边形四边形.
(1) .
(2)求边x,y的长度.
18.如图,平面直角坐标系中,的顶点都在正方形网格的格点上.
(1)以O点为位似中心,位似比的绝对值为2,将放大为,请在网格图中画出(只画出其中一种);
(2)若,的面积分别为S、,写出S、的数量关系.
19.如图,在△ABC中,D、E分别是边AC、BC的中点,F是BC延长线上一点,∠F=∠B.
(1)若AB=10,求FD的长;
(2)若AC=BC,求证:△CDE∽△DFE.
20.如图,矩形 中, 为 上一点, 于点 .
(1)证明 ;
(2)若 , , ,求 的长.
21.如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡在点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度DE=3.5m,点F到地面的高度CF=1.5m,灯泡到木板的水平距离AC=5.4m,墙到木板的水平距离为CD=4m.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上.
(1)求BC的长.
(2)求灯泡到地面的高度AG.
22.如图,的三个顶点坐标分别为.
(1)直接写出关于轴对称的三个顶点的坐标;
(2)画出绕点逆时针旋转后的;
(3)以点为位似中心,在网格中画出的位似图形,使与的相似比为.
23.综合问题:从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,DC= - ,BD= ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求CB长.
答案解析部分
1.【答案】B
2.【答案】C
【解析】【解答】解:∵ ,
∴ ,即 ,
∴ .
故答案为:C.
【分析】根据平行线分线段成比例定理“两条直线被一组平行线所截,截得的对应线段的长度成比例”可得比例式求解.
3.【答案】D
【解析】【解答】解:A、两个直角三角形的边不一定成比例,角不一定相等,不一定相似,故本选项不符合题意;
B、两个等腰三角形的边不一定成比例,角不一定相等,不一定相似,故本选项不符合题意;
C、两个矩形的对应角相等,但对应边不一定成比例,不一定相似,故本选项不符合题意;
D、两个等腰直角三角形的对应边一定成比例,对应角一定相等,所以一定相似,故本选项符合题意.
故答案为:D.
【分析】根据相似图形的对应边成比例,对应角相等,结合直角三角形、等腰三角形、矩形以及等腰直角三角形的特点对各选项进行分析判断.
4.【答案】A
【解析】【解答】根据黄金比的定义得: ,得 .
故答案为:A.
【分析】先求出,再根据AB=4计算求解即可。
5.【答案】C
【解析】【解答】解:∵
又∵∠DAE=∠CAB
∴△DAE∽△CAB
∴
∴DE=BC==
故答案为:C.
【分析】由两边对应成比例且夹角相等的两个三角形相似,可得△DAE∽△CAB,相似三角形的对应边之比等于相似比得,从而代入可算出DE的长.
6.【答案】A
【解析】【解答】解:∵M和N分别为AB和CD的中点,
∴矩形ABCD的面积是矩形MNCB的面积的2倍,
∵果矩形ABCD∽矩形MNCB
∴矩形ABCD与矩形MNCB的相似比为 .
故答案为:A.
【分析】根据相似多边形的性质,面积的比是相似比的平方,即可得解.
7.【答案】A
【解析】【解答】解:
A:没有能判定相似的条件,故不相似,不符合题意;
B:两角相等,故相似,符合题意;
C:两边对应成比例且夹角相等,故相似,符合题意;
D:两角相等,故相似,符合题意;
故答案为:A.
【分析】利用相似三角形的判定条件进行逐一判断即可求解.
8.【答案】B
【解析】【解答】解:根据题意,作△EFC,树高为CD,且∠ECF=90°,ED=2m,FD=8m;
∵∠E+∠F=90°,∠E+∠ECD=90°,
∴∠ECD=∠F,
又
∴△EDC∽△CDF,
∴,即DC2=ED FD=2×8=16,
解得CD=4m(负值舍去).
故答案为:B.
【分析】如图,证明△EDC∽△CDF,利用相似三角形对应边成比例即可求解.
9.【答案】B
【解析】【解答】解:由题意可知:
AB,
所以,,
所以且相似比为2:1,
因为,
所以,故A选项错误,不符合题意;
因为,
所以,故B选项正确,符合题意;
因为,
所以故C、D选项错误,不符合题意;
故选:B.
【分析】分别求出AB=、、,再依据相似三角形的性质进行判断即可.
10.【答案】C
【解析】【解答】解:如图,过P作交AB于D,作交AC于E,则,;
过P作,交AB于F,则,此时,;
过P作,交AC于F,则,此时,,;
当时,有4种不同的剪法;当时,有3种不同的剪法,甲和乙对,丙错 .
故答案为:C.
【分析】根据相似三角形的对应边成比例,得到的长的取值范围.
11.【答案】6
【解析】【解答】设,
∴a=6k,b=5k,c=4k,
∵,
∴6k+5k-8k=3,
解得:k=1,
∴a=6×1=6,
故答案为:6.
【分析】设,可得a=6k,b=5k,c=4k,再结合求出k的值,最后求出a的值即可.
12.【答案】2
13.【答案】
【解析】【解答】如解图,过点 作 于 ,
∵ ,
∴ ,
∴ ,
∵ ,点 是 的中点,
∴ ,
∵ ,
∴ ∽
∴
∴ ,
设 为 ,则 ,由勾股定理得 ,
又∵ ,
∴ ,
则 ,
∵ 且 ,
∴ ∽ ,
∴ ,
即 ,
解得 ,
∴ .
∵
∴
∴
∴
故答案为:
【分析】过点 作 于 ,根据 ∽ 可得出AH,FH的关系式,然后根据 ∽ ,可得 ,构建方程即可求解即可。
14.【答案】
【解析】【解答】解:由题意,点C为线段AB的“近A,6阶黄金分割点”时,,
∴,
∵,
∴,
∵,
∴,
即:,
整理得:,
解得:或,
经检验,或是上述分式方程的解,
∵,
∴,
故答案为:.
【分析】由题意得,则,再由=,即得,整理得,再解方程即可.
15.【答案】(1)解:因为,
设,则,
(2)解:令,得
所以,,.
【解析】【分析】(1)利用设k法可得:设,则, ,再将其代入计算即可;
(2)将,,代入求出k的值,再求出a、b、c的值即可.
16.【答案】解:∵AE∥DF,
∴,即,
∴EF=4,
∴BE=BF+EF=6+4=10,
∵DE∥AC,
∴,即 ,
∴CE=,
∴CF=CE+EF=.
【解析】【分析】先根据平行线分线段成比例即可得到EF,进而即可得到BE,再根据平行线分线段成比例即可得到CE,进而即可求解。
17.【答案】(1)
(2)解:∵四边形四边形,
∴
解得,.
【解析】【解答】解:(1)∵已知四边形四边形
∴∠C=∠C'=135°
∴
故答案为:
【分析】(1)根据相似图形性质可得∠C=∠C'=135°,再根据四边形内角和定理即可求出答案.
(2)根据相似图形的相似比性质即可求出答案.
18.【答案】(1)解:如图所示:即为所求;(另一种同样给分)
(2)解:∵,位似比的绝对值为2,放大为,
∴和相似比为,
∴
即:.
【解析】【分析】(1)利用位似图形的性质求得A、B、C对应点A1B1C1的位置,连接即可求解;
(2)利用位似图形的性质:面积比等于相似比的平方,代入数据即可求解.
19.【答案】(1)解:∵D、E分别是AC、BC的中点,
∴DE//AB, DE=AB=5
又∵DE//AB,
∴∠DEC= ∠B.
而∠ F= ∠ B,
∴∠DEC =∠B,
∴FD=DE=5
(2)解:∵AC=BC,
∴∠A=∠B.
又∠CDE=∠A,∠CED= ∠B,
∴∠CDE=∠B.
而∠B=∠F,
∴∠CDE=∠F,∠CED=∠DEF,
∴△CDE∽△DFE .
【解析】【分析】(1)根据平行线的性质可得∠DEC= ∠B,再结合∠F= ∠B,可得∠DEC =∠B,最后利用等角对等边的性质可得FD=DE=5;
(2)证明∠CDE=∠F,∠CED=∠DEF,即可证明△CDE∽△DFE。
20.【答案】(1)证明:∵四边形 是矩形,
∴ , ,
∴ ,
∵ ,
∴ ,
在 和 中, ,
∴ ;
(2)解:∵在 中, , ,
,
由(1)已证: ,
∴ ,即 ,
解得 .
【解析】【分析】(1)根据四边形 是矩形,得出 , ,再根据垂直的定义得出 ,利用全等三角形的性质得出 ;
(2)在 中, , ,利用勾股定理得出AE的值,由(1)已证: ,得出 ,解得即可。
21.【答案】(1)解:由题意可得:FC∥DE,
则△BFC∽△BED,
故,
即,
解得:BC=3,
经检验,BC=3是上述分式方程的解,
∴BC的长为3m;
(2)解:∵AC=5.4m,
∴AB=5.4-3=2.4(m),
∵光在镜面反射中的入射角等于反射角,
∴∠FBC=∠GBA,
又∵∠FCB=∠GAB,
∴△BGA∽△BFC,
∴,
∴,
解得:AG=1.2(m),
∴灯泡到地面的高度AG为1.2m.
【解析】【分析】(1)先证明△BFC∽△BED,可得,将数据代入可得,再求出BC的长即可;
(2)先证明△BGA∽△BFC,可得,将数据代入可得,再求出AG的长即可。
22.【答案】(1)解:
(2)解:绕点逆时针旋转,如图所示,
即为所求图形的位置.
(3)解:∵,,,点为位似中心,相似比为,即位似比为,
∴,,,
∴延长到,使得,即,延长到,使得,即,连接,,得;
反向延长到,使得,即,反向延长到,使得,即,连接,,得,如图所示,
∴点为位似中心,相似比为,,都是所求图形.
【解析】【解答】解:(1)关于轴对称的三个顶点的坐标,横坐标变为原来的相反数,纵坐标不变,,
∴.
【分析】(1)关于y轴对称的点:横坐标互为相反数,纵坐标相同,据此不难得到点A1、B1、C1的坐标;
(2)根据旋转的性质,分别将点A、B、C绕点O逆时针旋转90°得到点A2、B2、C2,然后顺次连接即可;
(3)分别延长AB、CB,或反向延长BA、BC,使A3B=2AB,C3B=2CB,然后顺次连接即可.
23.【答案】(1)证明:∵∠ A=40°,∠ B=60°,
∴ ∠ACB=180°-∠A-∠B=80°,
∵∠A ∠B ∠ACB,∴ △ABC不是等腰三角形.
∵CD平分∠ ACB,∴ ∠ACD=∠BCD= ∠ACB=40°,
∴ ∠ACD=∠ A=40°,∴ △ACD为等腰三角形.∴ ∠DCB=∠ A=40°,
∠CBD=∠ ABC, ∴ △BCD∽△BAC,∴ CD是△ABC的完美分割线.
(2)解:①如图3所示,
当AD=CD时,∠ACD=∠ A=48°,根据完美分割线的定义,可得△BDC∽△BCA,∴∠BCD=∠A=48°,则∠ACB=∠ACD+∠BCD=96°.
②如图4所示,
当AD=AC时,∠ACD=∠ ADC= ,
根据完美分割线的定义,可得△BDC∽△BCA,∴∠BCD=∠A=48°,
∴∠ACB=∠ACD+∠BCD=114°.
③如图5所示,
当AC=CD时,∠ADC=∠ A=48°.∵△BDC∽△BCA,∴∠BCD=∠A=48°,根据完美分割线的定义,可得△BDC∽△BCA,∴∠BCD=∠A=48°,
∴这与∠ADC>∠BCD矛盾,所以图5的情况不符合题意.
综上所述,∠ACB的度数为96°或114°.
(3)解:∵△ACD是以CD为底边的等腰三角形,AC=2,∴AC=AD=2.
∵△BCD∽△BAC,∴
,解得BC=
写成:BC= 或者BC= ,所有结果没化简均不扣分
【解析】【分析】(1)首先由三角形内角和定理求出∠ACB的度数,然后根据∠A、∠B、∠ACB的度数的关系即可判断出△ABC是否为等腰三角形,由角平分线的定义求出∠ACD、∠BCD的度数,然后根据相似三角形的判定定理解答即可;
(2)分①AD=CD,②AD=AC,③AC=CD三种情况, 根据完美分割线的定义,可得△BDC∽△BCA, 由相似三角形的性质可得∠BCD=∠A,最后由角的和差关系求解即可;
(3)首先由等腰三角形的性质可得AC=AD=2,然后由相似三角形对应边成比例就可求出BC的值.
1 / 1
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
