人教版九年级数学上册第二十四章 圆 单元复习题(含解析)
文档属性
| 名称 | 人教版九年级数学上册第二十四章 圆 单元复习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 978.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 00:00:00 | ||
图片预览




文档简介
人教版九年级数学上册第二十四章圆单元复习题
一、选择题
1.已知的半径是,则中最长的弦长是( )
A. B. C. D.
2. 如图,⊙O的半径为10,弦长AB=16,弦心距OC的长为( )
A.5 B.6 C.7 D.8
3.如图,在中,若,则的度数是( )
A.15° B.25° C.50° D.75°
4.如图,在中,弦AC与半径OB交于点D,连接OA,BC.若,,则的度数为( )
A.110° B.112° C.120° D.132°
5.已知点P在半径为的圆内,则点P到圆心的距离可以是( )
A. B. C. D.
6.如图,已知⊙O的直径CD=8,AB是⊙O的弦,AB⊥CD,垂足为M,OM=2,则AB的长为( )
A.2 B. C.4 D.
7.如图,四边形ABCD内接于⊙O,D是的中点,若∠B=70°,则∠CAD的度数为( )
A.70° B.55° C.35° D.20°
8.在平面直角坐标系中,以原点为圆心,为半径作圆,点的坐标是,则点与的位置关系是( )
A.点在内 B.点在外
C.点在上 D.点在上或在外
9.如图,点O是内切圆的圆心,已知,则的度数是( )
A. B. C. D.
10.我国古代数学家刘徽利用圆内接正多边形创立了“割圆术”,现将半径为2的圆十二等分构造出2个矩形和1个正方形(如图),则阴影部分的面积是( )
A.1 B. C. D.
二、填空题
11.如图,在中,半径垂直弦于点D,若,,则的长为 .
12.如图,是的切线,是切点,连结、若,则的大小为 度
13.如图所示,四边形为的内接四边形,,则的大小是 .
14.如图,在Rt中,,分别以各边为直径作半圆,图中阴影部分在数学史上被称为“希波克拉底月牙”.当时,阴影部分的面积为 .
三、解答题
15.已知:如图,OA,OB是⊙O的两条半径,点C,D分别在OA,OB上,且AC=BD.求证:AD=BC.
16.如图,AB是的直径,,于点E,连接BD交CE于点F.
(1)求证:.
(2)若,,求弦BD的长.
17. 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB.求证:直线AB是O的切线.
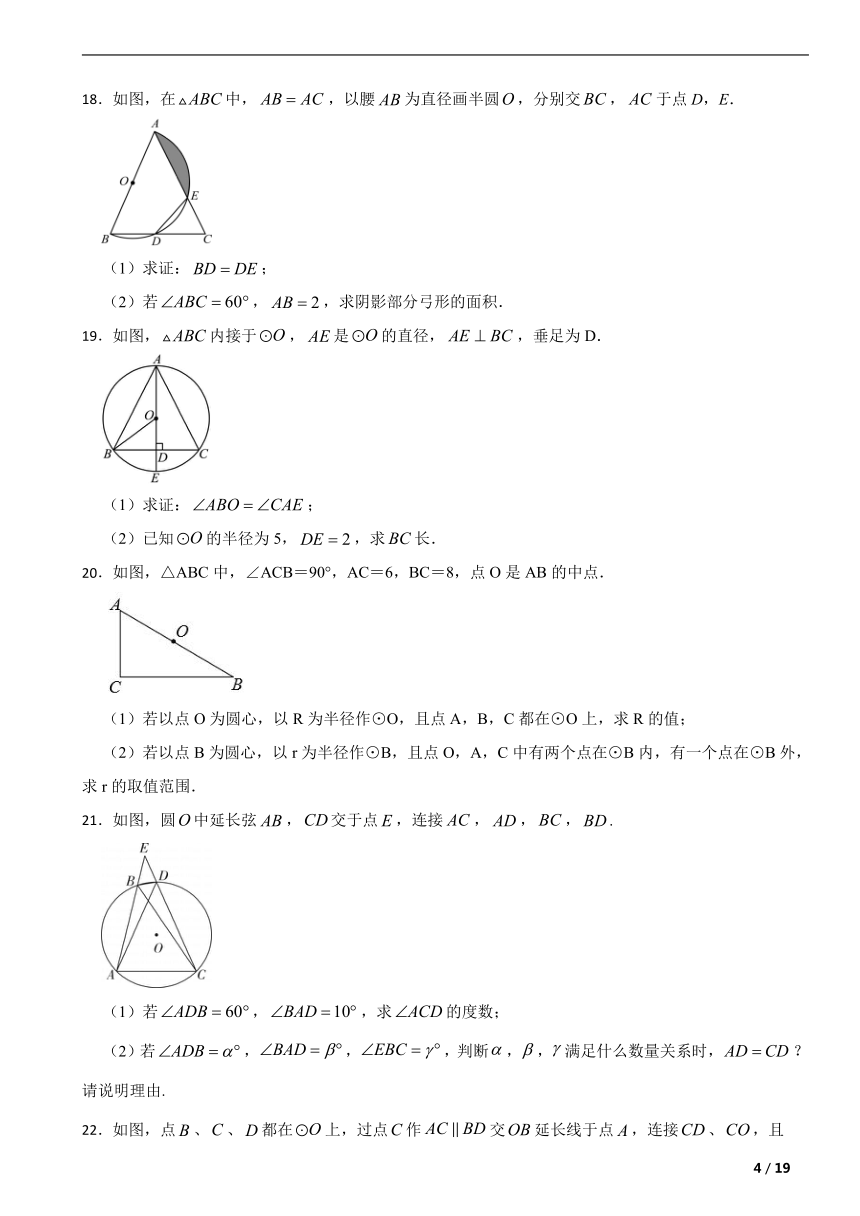
18.如图,在中,,以腰为直径画半圆,分别交,于点D,E.
(1)求证:;
(2)若,,求阴影部分弓形的面积.
19.如图,内接于,是的直径,,垂足为D.
(1)求证:;
(2)已知的半径为5,,求长.
20.如图,△ABC中,∠ACB=90°,AC=6,BC=8,点O是AB的中点.
(1)若以点O为圆心,以R为半径作⊙O,且点A,B,C都在⊙O上,求R的值;
(2)若以点B为圆心,以r为半径作⊙B,且点O,A,C中有两个点在⊙B内,有一个点在⊙B外,求r的取值范围.
21.如图,圆中延长弦,交于点,连接,,,.
(1)若,,求的度数;
(2)若,,,判断,,满足什么数量关系时,?请说明理由.
22.如图,点、、都在上,过点作交延长线于点,连接、,且,cm.
(1)求证:是的切线;
(2)求的半径长;
(3)求由弦、与弧所围成的阴影部分的面积.
23.已知,是直径,弦于点,点是上一点.
(1)如图1,连接、、,求证:平分;
(2)如图2,连接、、,交于点,交于点,若;求证:;
(3)如图,在(2)的条件下,连接交于,连接,若,,求半径.
答案解析部分
1.【答案】B
【解析】【解答】解:的半径是,中最长的弦长是直径等于, 中最长的弦长是 .
故答案为:B.
【分析】根据圆的定义,和弦长的概念求解.
2.【答案】B
【解析】【解答】解: 弦心距.
故答案为:B.
【分析】根据垂径定理和勾股定理,代入求解.
3.【答案】C
【解析】【解答】解:由题意可得:
故答案为:C
【分析】根据同弧所对的圆周角是圆心角的一半即可求出答案.
4.【答案】B
【解析】【解答】解:∵∠ADB=∠B+∠ACB
∴∠ACB=∠ADB-∠B=116°-60°=56°
∴∠AOB=2∠ACB=112°
故答案为:B.
【分析】三角形的外角等于与它不相邻的两个内角之和,所以∠ADB=∠B+∠ACB,求得∠ACB=∠ADB-∠B=56°;在同一个圆中,圆心角是同弧所对圆周角的2倍,所以∠AOB=2∠ACB=112°.
5.【答案】A
【解析】【解答】解: ∵点P在半径为的圆内 ,
∴ 点P到圆心的距离<5cm,
∴ 点P到圆心的距离可以是2cm.
故答案为:A.
【分析】设⊙O的半径为r,点到圆心O的距离为d,当d<r时,点在圆内;当d=r时,点在圆上,当d>r时,点在圆外,据此解答即可.
6.【答案】D
7.【答案】C
【解析】【解答】解:∵∠B=70°,
∴ 的度数是140°,
∵D是 的中点,
∴ 和 的度数都是70°,
∴∠CAD= 70°=35°,
故答案为:C.
【分析】根据圆心角、弧、弦的关系可得弧ADC的度数,进而根据中点的定义可得弧AD与弧CD的度数,最后根据圆周角的度数等于所对弧的度数的一半即可得出答案.
8.【答案】C
【解析】【解答】解:∵圆心O的坐标为,点P的坐标为,
∴,因而点P在上.
故答案为:B
【分析】先根据勾股定理求出OP,进而根据点与圆的位置关系即可求解。
9.【答案】B
【解析】【解答】解:∵点O是△ABC的内切圆,
∴OB、OC分别是∠ABC、∠ACB的平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∵∠ABC=50°,∠ACB=80°,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(50°+80°)=65°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-65°=115°.
故答案为:B.
【分析】根据三角形的内切圆的圆心是三角形内角平分线的交点可得OB、OC分别是∠ABC、∠ACB的平分线,于是结合已知可求得∠OBC+∠OCB的度数,再根据三角形内角和定理即可求解.
10.【答案】C
【解析】【解答】解:如图所示:阴影部分为八个全等的等腰直角三角形,
分别连接AO,OB,OC,
∴OA=OB=OC=2,
∵将半径为2的圆十二等分构造出2个矩形和1个正方形 ,
∴∠1=∠2=30°,
又∵OC⊥AD与点D,
∴∠3=30°,
∴OD=DC=1,AD=,
∴一个小的等腰直角三角形的直角边为AE=-1,
∴阴影部分的面积为:8××(-1) =4×(3-2+1)=16-8.
故答案为:C.
【分析】“割圆术”将半径为2的圆十二等分构造出2个矩形和1个正方形,阴影部分为八个全等的等腰直角三角形,所以只需要求出一个等腰直角三角形的直角边即可解决问题.先根据十二等分求出一等分的圆心角,从而求出∠3的度数为30°,在直角三角形ODA中求解AE,最后根据三角形面积公式计算出整个阴影部分的面积即可.
11.【答案】2
【解析】【解答】解:连接OA
∵在中,半径垂直弦于点D,
∴
∵OC=3
∴OA=OC=3
在Rt△AOD中,
∴CD=3-1=2
故答案为:2
【分析】连接OA ,根据垂径定理可得,再根据勾股定理即可求出答案.
12.【答案】54
【解析】【解答】∵MN是的切线,是切点,
∴∠OMN=90°,
∵∠N=36°,
∴∠MON=180°-∠OMN-∠N=180°-90°-36°=54°,
故答案为:54.
【分析】利用切线的性质可得∠OMN=90°,再利用三角形的内角和求出∠MON的度数即可.
13.【答案】120°
【解析】【解答】解:∵四边形为的内接四边形,,
∴∠BAD=60°,
∴∠BOD=120°,
故答案为:120°
【分析】先根据圆内接四边形的性质得到∠BAD=60°,进而根据圆周角定理即可求解。
14.【答案】16
【解析】【解答】解:在Rt△ABC中,∠C=90°,,以AC为直径的半圆的面积为:,以BC为直径的半圆的面积为:,以AB为直径的半圆的面积为:,,∴S阴影=8π+2π+16-10π=16,
故答案为:16.
【分析】本题考查了勾股定理,半圆面积的计算,正确得出阴影部分面积的计算方法是解题的关键.根据勾股定理求出AB的长,再分别求出以AC为直径的半圆的面积与以BC为直径的半圆的面积以及以AB为直径的半圆的面积与△ABC的面积,即可求解.
15.【答案】证明:∵OA,OB是⊙O的两条半径,
∴AO= BO,
∵点C,D分别在OA,OB上,且AC=BD,
∴ OC=OD ,
在△OCB与△ODA中,
∴△OCB≌△ODA(SAS),
∴ AD= BC.
【解析】【分析】先分别说明AO= BO,OC=OD,通过SAS来证明 △OCB≌△ODA ,从而可得AD= BC.
16.【答案】(1)解:证明:∵AB是的直径,
∴,∴
∵,∴,
∴,
∴
又∵,∴,
∴,
∴,∴;
(2)解:连接OC,交BD于点G,
∵,∴,,
∵,,,
∴,
∴的半径为10,
设,则,
由勾股定理,得,
即,
解得,
∴,
∴
17.【答案】证明:连接OC,如图
∵OA= OB,CA= CB,
∴OC⊥AB,
又∵OC是O的半径,
∴直线AB是⊙O的切线.
【解析】【分析】 连接OC,由OA= OB,CA= CB,根据等腰三角形的性质得到OC⊥AB, 又因为点C在 ⊙O上 ,利用切线的判定定理即可求解,可以简记为“点在圆上,连半径,证垂直”即可.
18.【答案】(1)解:解:如图,连接,
为直径,
,
,
,
弧弧,
;
(2)解:如图,连接,过点作于点,
,
,
,,
为等边三角形,
,
又,
为等边三角形,
,,,
.
【解析】【分析】(1)在圆中,直径所对的圆周角为直角,连接AD,则AD⊥BC,由AB=AC,根据等腰三角形“三线合一”可知,AD是∠BAC的平分线,故∠BAD=∠CAD,BD =DE ,BD=DE.
(2)S弓形=S扇形-S△,要求弓形的面积,先求扇形和三角形的面积;连接OE,由已知可得△AOE是等边三角形,扇形OAE是60°的扇形,根据题中所给数据,求出即可,
19.【答案】(1)证明:∵是的直径,,
∴,
∴,
∵,
∴是等腰三角形,
∴,
∴;
(2)解:∵是的直径,,
∴,,
在中,,,
∴,
∴.
【解析】【分析】(1)根据垂径定理可得,再根据 是等腰三角形,可得,即可得到;
(2)先求出,OB=5,利用勾股定理求出BD的长,再求出即可。
20.【答案】(1)解:∵∠ACB=90°,AC=6,BC=8,
∴AB==10,
∵∠ACB=90°,点A,B,C都在⊙O上,
∴AB为⊙O的直径,
∴R=AB=5.
(2)解:∵点O是AB的中点,AB=10,
∴BO=AB=5,
∴BO<BC<BA,
∵点O,A,C中有两个点在⊙B内,有一个点在⊙B外,
∴点O、C在⊙B内部,点A在⊙B外,
∴8<r<10.
【解析】【分析】(1)先利用勾股定理求出AB的长,再利用直角三角形斜边上中线的性质可得R的值;
(2)先利用直角三角形斜边上中线的性质求出BO的长,再利用点和圆的位置关系求出r的取值范围即可。
21.【答案】(1)解:∵,,
∴∠ACB=∠ADB=60°,∠BCD=∠BAD=10°,
∴∠ACD=∠ACB+∠BCD=60°+10°=70°
(2)解:当γ=2(α+β)时,AD=CD,
∵,,
∴∠ACB=∠ADB=α°,∠BAD=∠BCD=β°,
∴∠ACD=∠ACB+∠BCD=α°+β°,
∵AD=CD,
∴∠ACD=∠DAC,
∵,
∴∠CAD=∠CBD=∠ACD,
∵∠DBA+∠ACD=180°,∠EBD+∠DBA=180°,
∴∠ACD=∠EBD,
∴∠EBC=∠EBD+∠DBC=2∠ACD=γ°,
∴γ=2(α+β)
【解析】【分析】(1)利用同弧所对的圆周角相等,可求出∠ACB,∠BCD的度数,再根据∠ACD=∠ACB+∠BCD,代入计算求出∠ACD的度数.
(2)利用同弧所对的圆周角相等,可证得∠ACB=∠ADB=α°,∠BAD=∠BCD=β°,可得到∠ACD=α°+β°,利用等边对等角可证得∠ACD=∠DAC,再利用圆周角定理可得到∠CAD=∠CBD=∠ACD,利用圆内接四边形的性质可得到∠ACD=∠EBD,由此可推出∠EBC=2∠ACD,即可证得结论.
22.【答案】(1)证明:设OC、BD相交于点E
∵∠CDB=∠OBD=30°,
∴∠BOE=60°
∵∠OBD=30°
∴∠BEO=90°
即OE⊥BD
又∵AC∥BD
∴OC⊥AC
∵OC是⊙O的半径
∴AC为⊙O切线.
(2)解:在△OBE中,∠BEO=90°,,∠OBE=30
∴
∴
解得R=6
即⊙O的半径长为6cm
(3)解:在△CDE和△OBE中
∴△CDE≌△OBE(ASA)
∴
【解析】【分析】(1)先利用圆周角定理证得OE⊥BD,再通过平行线的性质得到AC为⊙O切线.
(2)利用垂径定理求得BE长,再通过的直角三角形得到半径长.
(3)通过ASA判定△CDE≌△OBE证得阴影部分面积等于扇形OBC的面积,再利用扇形面积公式求得阴影部分面积.
23.【答案】(1)证明: 是 直径, ,
∴ ,
,
平分 ;
(2)证明:设 ,
,
,
,
,
,
,
,
∵ ,
,
,
,
,
,
,
,
如图2,连接 ,
,
∴△DFE≌△DFP(SAS) ,
,
, , ,
∴△CEH≌△DEH(ASA) ,
,
;
(3)解:如图3,连接 EG 、 CO ,
设 ,
为直径, ,
∴ ,
,由 知 ,
, ,
,
,
在 和 中,
,
∴△AFE≌△AFP(SAS) ,
,
,
∴AG为EP的中垂线,
,
,
∵AB为直径,
,
,
,
在 和 中,
, , ,
∴△AEG≌△APG(SSS) ,
,
, ,
,
,
,
,
,
,
设半径为 , ,
则 ,
∵ ,
,
,
,
,
,
,
在 和 中,
, , ,
∴△CHO≌△BGE(AAS) ,
,
,
,
,
,
在 中,由勾股定理得 ,
即 ,
,
,
则 ,
,
即 ,
令 ,
则原式为 ,
即 ,
解得: , 舍 ,
,
负值舍去 .
半径为10.
【解析】【分析】(1)根据垂径定理得,根据等弧所对的圆周角相等得∠BPC=∠BPD,据此即可得出结论;
(2)∠DCP=α,根据圆周角定理证明∠BAD=∠PAD,连接OD,利用SAS证明△DFE≌△DFP,可得DP=DE,再永AAS证明△CEH≌△DEH,可得CE=DE,进而可以解决问题;
(3)连接EG、CO,利用SAS证明△AEF≌△APF,可得EF=PF,再利用SSS证明△AEG≌△APG,可得∠AEG=∠APG=90°,利用等角对等边证明BO=BG,设半径为r,HC=a,用AAS证△CHO≌△BGE,可得HC=BE=a,根据S△AOG=30,可得EG=,然后在Rt△EBG中利用勾股定理即可解决问题.
1 / 1
一、选择题
1.已知的半径是,则中最长的弦长是( )
A. B. C. D.
2. 如图,⊙O的半径为10,弦长AB=16,弦心距OC的长为( )
A.5 B.6 C.7 D.8
3.如图,在中,若,则的度数是( )
A.15° B.25° C.50° D.75°
4.如图,在中,弦AC与半径OB交于点D,连接OA,BC.若,,则的度数为( )
A.110° B.112° C.120° D.132°
5.已知点P在半径为的圆内,则点P到圆心的距离可以是( )
A. B. C. D.
6.如图,已知⊙O的直径CD=8,AB是⊙O的弦,AB⊥CD,垂足为M,OM=2,则AB的长为( )
A.2 B. C.4 D.
7.如图,四边形ABCD内接于⊙O,D是的中点,若∠B=70°,则∠CAD的度数为( )
A.70° B.55° C.35° D.20°
8.在平面直角坐标系中,以原点为圆心,为半径作圆,点的坐标是,则点与的位置关系是( )
A.点在内 B.点在外
C.点在上 D.点在上或在外
9.如图,点O是内切圆的圆心,已知,则的度数是( )
A. B. C. D.
10.我国古代数学家刘徽利用圆内接正多边形创立了“割圆术”,现将半径为2的圆十二等分构造出2个矩形和1个正方形(如图),则阴影部分的面积是( )
A.1 B. C. D.
二、填空题
11.如图,在中,半径垂直弦于点D,若,,则的长为 .
12.如图,是的切线,是切点,连结、若,则的大小为 度
13.如图所示,四边形为的内接四边形,,则的大小是 .
14.如图,在Rt中,,分别以各边为直径作半圆,图中阴影部分在数学史上被称为“希波克拉底月牙”.当时,阴影部分的面积为 .
三、解答题
15.已知:如图,OA,OB是⊙O的两条半径,点C,D分别在OA,OB上,且AC=BD.求证:AD=BC.
16.如图,AB是的直径,,于点E,连接BD交CE于点F.
(1)求证:.
(2)若,,求弦BD的长.
17. 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB.求证:直线AB是O的切线.
18.如图,在中,,以腰为直径画半圆,分别交,于点D,E.
(1)求证:;
(2)若,,求阴影部分弓形的面积.
19.如图,内接于,是的直径,,垂足为D.
(1)求证:;
(2)已知的半径为5,,求长.
20.如图,△ABC中,∠ACB=90°,AC=6,BC=8,点O是AB的中点.
(1)若以点O为圆心,以R为半径作⊙O,且点A,B,C都在⊙O上,求R的值;
(2)若以点B为圆心,以r为半径作⊙B,且点O,A,C中有两个点在⊙B内,有一个点在⊙B外,求r的取值范围.
21.如图,圆中延长弦,交于点,连接,,,.
(1)若,,求的度数;
(2)若,,,判断,,满足什么数量关系时,?请说明理由.
22.如图,点、、都在上,过点作交延长线于点,连接、,且,cm.
(1)求证:是的切线;
(2)求的半径长;
(3)求由弦、与弧所围成的阴影部分的面积.
23.已知,是直径,弦于点,点是上一点.
(1)如图1,连接、、,求证:平分;
(2)如图2,连接、、,交于点,交于点,若;求证:;
(3)如图,在(2)的条件下,连接交于,连接,若,,求半径.
答案解析部分
1.【答案】B
【解析】【解答】解:的半径是,中最长的弦长是直径等于, 中最长的弦长是 .
故答案为:B.
【分析】根据圆的定义,和弦长的概念求解.
2.【答案】B
【解析】【解答】解: 弦心距.
故答案为:B.
【分析】根据垂径定理和勾股定理,代入求解.
3.【答案】C
【解析】【解答】解:由题意可得:
故答案为:C
【分析】根据同弧所对的圆周角是圆心角的一半即可求出答案.
4.【答案】B
【解析】【解答】解:∵∠ADB=∠B+∠ACB
∴∠ACB=∠ADB-∠B=116°-60°=56°
∴∠AOB=2∠ACB=112°
故答案为:B.
【分析】三角形的外角等于与它不相邻的两个内角之和,所以∠ADB=∠B+∠ACB,求得∠ACB=∠ADB-∠B=56°;在同一个圆中,圆心角是同弧所对圆周角的2倍,所以∠AOB=2∠ACB=112°.
5.【答案】A
【解析】【解答】解: ∵点P在半径为的圆内 ,
∴ 点P到圆心的距离<5cm,
∴ 点P到圆心的距离可以是2cm.
故答案为:A.
【分析】设⊙O的半径为r,点到圆心O的距离为d,当d<r时,点在圆内;当d=r时,点在圆上,当d>r时,点在圆外,据此解答即可.
6.【答案】D
7.【答案】C
【解析】【解答】解:∵∠B=70°,
∴ 的度数是140°,
∵D是 的中点,
∴ 和 的度数都是70°,
∴∠CAD= 70°=35°,
故答案为:C.
【分析】根据圆心角、弧、弦的关系可得弧ADC的度数,进而根据中点的定义可得弧AD与弧CD的度数,最后根据圆周角的度数等于所对弧的度数的一半即可得出答案.
8.【答案】C
【解析】【解答】解:∵圆心O的坐标为,点P的坐标为,
∴,因而点P在上.
故答案为:B
【分析】先根据勾股定理求出OP,进而根据点与圆的位置关系即可求解。
9.【答案】B
【解析】【解答】解:∵点O是△ABC的内切圆,
∴OB、OC分别是∠ABC、∠ACB的平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∵∠ABC=50°,∠ACB=80°,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(50°+80°)=65°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-65°=115°.
故答案为:B.
【分析】根据三角形的内切圆的圆心是三角形内角平分线的交点可得OB、OC分别是∠ABC、∠ACB的平分线,于是结合已知可求得∠OBC+∠OCB的度数,再根据三角形内角和定理即可求解.
10.【答案】C
【解析】【解答】解:如图所示:阴影部分为八个全等的等腰直角三角形,
分别连接AO,OB,OC,
∴OA=OB=OC=2,
∵将半径为2的圆十二等分构造出2个矩形和1个正方形 ,
∴∠1=∠2=30°,
又∵OC⊥AD与点D,
∴∠3=30°,
∴OD=DC=1,AD=,
∴一个小的等腰直角三角形的直角边为AE=-1,
∴阴影部分的面积为:8××(-1) =4×(3-2+1)=16-8.
故答案为:C.
【分析】“割圆术”将半径为2的圆十二等分构造出2个矩形和1个正方形,阴影部分为八个全等的等腰直角三角形,所以只需要求出一个等腰直角三角形的直角边即可解决问题.先根据十二等分求出一等分的圆心角,从而求出∠3的度数为30°,在直角三角形ODA中求解AE,最后根据三角形面积公式计算出整个阴影部分的面积即可.
11.【答案】2
【解析】【解答】解:连接OA
∵在中,半径垂直弦于点D,
∴
∵OC=3
∴OA=OC=3
在Rt△AOD中,
∴CD=3-1=2
故答案为:2
【分析】连接OA ,根据垂径定理可得,再根据勾股定理即可求出答案.
12.【答案】54
【解析】【解答】∵MN是的切线,是切点,
∴∠OMN=90°,
∵∠N=36°,
∴∠MON=180°-∠OMN-∠N=180°-90°-36°=54°,
故答案为:54.
【分析】利用切线的性质可得∠OMN=90°,再利用三角形的内角和求出∠MON的度数即可.
13.【答案】120°
【解析】【解答】解:∵四边形为的内接四边形,,
∴∠BAD=60°,
∴∠BOD=120°,
故答案为:120°
【分析】先根据圆内接四边形的性质得到∠BAD=60°,进而根据圆周角定理即可求解。
14.【答案】16
【解析】【解答】解:在Rt△ABC中,∠C=90°,,以AC为直径的半圆的面积为:,以BC为直径的半圆的面积为:,以AB为直径的半圆的面积为:,,∴S阴影=8π+2π+16-10π=16,
故答案为:16.
【分析】本题考查了勾股定理,半圆面积的计算,正确得出阴影部分面积的计算方法是解题的关键.根据勾股定理求出AB的长,再分别求出以AC为直径的半圆的面积与以BC为直径的半圆的面积以及以AB为直径的半圆的面积与△ABC的面积,即可求解.
15.【答案】证明:∵OA,OB是⊙O的两条半径,
∴AO= BO,
∵点C,D分别在OA,OB上,且AC=BD,
∴ OC=OD ,
在△OCB与△ODA中,
∴△OCB≌△ODA(SAS),
∴ AD= BC.
【解析】【分析】先分别说明AO= BO,OC=OD,通过SAS来证明 △OCB≌△ODA ,从而可得AD= BC.
16.【答案】(1)解:证明:∵AB是的直径,
∴,∴
∵,∴,
∴,
∴
又∵,∴,
∴,
∴,∴;
(2)解:连接OC,交BD于点G,
∵,∴,,
∵,,,
∴,
∴的半径为10,
设,则,
由勾股定理,得,
即,
解得,
∴,
∴
17.【答案】证明:连接OC,如图
∵OA= OB,CA= CB,
∴OC⊥AB,
又∵OC是O的半径,
∴直线AB是⊙O的切线.
【解析】【分析】 连接OC,由OA= OB,CA= CB,根据等腰三角形的性质得到OC⊥AB, 又因为点C在 ⊙O上 ,利用切线的判定定理即可求解,可以简记为“点在圆上,连半径,证垂直”即可.
18.【答案】(1)解:解:如图,连接,
为直径,
,
,
,
弧弧,
;
(2)解:如图,连接,过点作于点,
,
,
,,
为等边三角形,
,
又,
为等边三角形,
,,,
.
【解析】【分析】(1)在圆中,直径所对的圆周角为直角,连接AD,则AD⊥BC,由AB=AC,根据等腰三角形“三线合一”可知,AD是∠BAC的平分线,故∠BAD=∠CAD,BD =DE ,BD=DE.
(2)S弓形=S扇形-S△,要求弓形的面积,先求扇形和三角形的面积;连接OE,由已知可得△AOE是等边三角形,扇形OAE是60°的扇形,根据题中所给数据,求出即可,
19.【答案】(1)证明:∵是的直径,,
∴,
∴,
∵,
∴是等腰三角形,
∴,
∴;
(2)解:∵是的直径,,
∴,,
在中,,,
∴,
∴.
【解析】【分析】(1)根据垂径定理可得,再根据 是等腰三角形,可得,即可得到;
(2)先求出,OB=5,利用勾股定理求出BD的长,再求出即可。
20.【答案】(1)解:∵∠ACB=90°,AC=6,BC=8,
∴AB==10,
∵∠ACB=90°,点A,B,C都在⊙O上,
∴AB为⊙O的直径,
∴R=AB=5.
(2)解:∵点O是AB的中点,AB=10,
∴BO=AB=5,
∴BO<BC<BA,
∵点O,A,C中有两个点在⊙B内,有一个点在⊙B外,
∴点O、C在⊙B内部,点A在⊙B外,
∴8<r<10.
【解析】【分析】(1)先利用勾股定理求出AB的长,再利用直角三角形斜边上中线的性质可得R的值;
(2)先利用直角三角形斜边上中线的性质求出BO的长,再利用点和圆的位置关系求出r的取值范围即可。
21.【答案】(1)解:∵,,
∴∠ACB=∠ADB=60°,∠BCD=∠BAD=10°,
∴∠ACD=∠ACB+∠BCD=60°+10°=70°
(2)解:当γ=2(α+β)时,AD=CD,
∵,,
∴∠ACB=∠ADB=α°,∠BAD=∠BCD=β°,
∴∠ACD=∠ACB+∠BCD=α°+β°,
∵AD=CD,
∴∠ACD=∠DAC,
∵,
∴∠CAD=∠CBD=∠ACD,
∵∠DBA+∠ACD=180°,∠EBD+∠DBA=180°,
∴∠ACD=∠EBD,
∴∠EBC=∠EBD+∠DBC=2∠ACD=γ°,
∴γ=2(α+β)
【解析】【分析】(1)利用同弧所对的圆周角相等,可求出∠ACB,∠BCD的度数,再根据∠ACD=∠ACB+∠BCD,代入计算求出∠ACD的度数.
(2)利用同弧所对的圆周角相等,可证得∠ACB=∠ADB=α°,∠BAD=∠BCD=β°,可得到∠ACD=α°+β°,利用等边对等角可证得∠ACD=∠DAC,再利用圆周角定理可得到∠CAD=∠CBD=∠ACD,利用圆内接四边形的性质可得到∠ACD=∠EBD,由此可推出∠EBC=2∠ACD,即可证得结论.
22.【答案】(1)证明:设OC、BD相交于点E
∵∠CDB=∠OBD=30°,
∴∠BOE=60°
∵∠OBD=30°
∴∠BEO=90°
即OE⊥BD
又∵AC∥BD
∴OC⊥AC
∵OC是⊙O的半径
∴AC为⊙O切线.
(2)解:在△OBE中,∠BEO=90°,,∠OBE=30
∴
∴
解得R=6
即⊙O的半径长为6cm
(3)解:在△CDE和△OBE中
∴△CDE≌△OBE(ASA)
∴
【解析】【分析】(1)先利用圆周角定理证得OE⊥BD,再通过平行线的性质得到AC为⊙O切线.
(2)利用垂径定理求得BE长,再通过的直角三角形得到半径长.
(3)通过ASA判定△CDE≌△OBE证得阴影部分面积等于扇形OBC的面积,再利用扇形面积公式求得阴影部分面积.
23.【答案】(1)证明: 是 直径, ,
∴ ,
,
平分 ;
(2)证明:设 ,
,
,
,
,
,
,
,
∵ ,
,
,
,
,
,
,
,
如图2,连接 ,
,
∴△DFE≌△DFP(SAS) ,
,
, , ,
∴△CEH≌△DEH(ASA) ,
,
;
(3)解:如图3,连接 EG 、 CO ,
设 ,
为直径, ,
∴ ,
,由 知 ,
, ,
,
,
在 和 中,
,
∴△AFE≌△AFP(SAS) ,
,
,
∴AG为EP的中垂线,
,
,
∵AB为直径,
,
,
,
在 和 中,
, , ,
∴△AEG≌△APG(SSS) ,
,
, ,
,
,
,
,
,
,
设半径为 , ,
则 ,
∵ ,
,
,
,
,
,
,
在 和 中,
, , ,
∴△CHO≌△BGE(AAS) ,
,
,
,
,
,
在 中,由勾股定理得 ,
即 ,
,
,
则 ,
,
即 ,
令 ,
则原式为 ,
即 ,
解得: , 舍 ,
,
负值舍去 .
半径为10.
【解析】【分析】(1)根据垂径定理得,根据等弧所对的圆周角相等得∠BPC=∠BPD,据此即可得出结论;
(2)∠DCP=α,根据圆周角定理证明∠BAD=∠PAD,连接OD,利用SAS证明△DFE≌△DFP,可得DP=DE,再永AAS证明△CEH≌△DEH,可得CE=DE,进而可以解决问题;
(3)连接EG、CO,利用SAS证明△AEF≌△APF,可得EF=PF,再利用SSS证明△AEG≌△APG,可得∠AEG=∠APG=90°,利用等角对等边证明BO=BG,设半径为r,HC=a,用AAS证△CHO≌△BGE,可得HC=BE=a,根据S△AOG=30,可得EG=,然后在Rt△EBG中利用勾股定理即可解决问题.
1 / 1
同课章节目录
