黑龙江试题汇编-02运算律(经典常考题)小学四年级数学下册人教版(带答案)
文档属性
| 名称 | 黑龙江试题汇编-02运算律(经典常考题)小学四年级数学下册人教版(带答案) |  | |
| 格式 | docx | ||
| 文件大小 | 58.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 15:48:35 | ||
图片预览




文档简介
黑龙江试题汇编-02运算律(经典常考题)-小学四年级数学下册(人教版)
一、选择题
1.(21·22四年级下·黑龙江绥化·期末)比较大小:99×99+199( )100×100。
A.= B.> C.<
2.(20·21四年级下·黑龙江牡丹江·期末)计算88×1002,最简便的算法是( )。
A.(90-2)×1002 B.88×(1000+2) C.80×1002+8×1002
3.(18·19四年级下·黑龙江鹤岗·期末)27×25×4=27×(25×4)运用了( )。
A.乘法交换律 B.乘法结合律 C.乖法分配律 D.乘法交换律与分配律
4.(17·18四年级下·黑龙江哈尔滨·期末)下列各式中,( )的计算是错误的。
A.195-45-55=195-(45+55) B.89×99=89×100-1 C.125×106×8=125×8×106
5.(17·18四年级下·黑龙江齐齐哈尔·期末)98×125×8﹦98×(125×8)这是根据( )。
A.乘法交换律 B.乘法结合律 C.乘法分配律
二、填空题
6.(21·22四年级下·黑龙江绥化·期末)42×37+42×62+42=42×( + + )
7.(21·22四年级下·黑龙江牡丹江·期末)在横线上填合适的数。
25×97=25×(100- ) (13×25)×40=13×( × )
8.(21·22四年级下·黑龙江七台河·期末)8×49×125=49×(8×125)运用了( )律和( )律。
9.(20·21四年级下·黑龙江牡丹江·期末)4×73×25=73×(4×25)运用了乘法的( )律和( )律。
10.(20·21四年级下·黑龙江七台河·期末)〇△□〇△□,运用了( ),用字母表示为( )。
11.(18·19四年级下·黑龙江绥化·期末)54×28+46×28=(54+46)×28这个算式运用了( )律。
12.(19·20四年级下·黑龙江鸡西·期末)4×a+a×5=( + )× 。
13.(19·20四年级下·黑龙江齐齐哈尔·期末)在横线上填上合适的数。
42×4×25= ×( × )
三、判断题
14.(21·22四年级下·黑龙江牡丹江·期末)125×11+8=125×8+11=1011。( )
15.(19·20四年级下·黑龙江齐齐哈尔·期末)35×(100+2)=35×100+2。( )
16.(19·20四年级下·黑龙江鸡西·期末)265×105-265×5=265×(105-5)。( )
四、计算题
17.(21·22四年级下·黑龙江绥化·期末)简算。
312×4+188×4 25×33×4 101×87
9.14-1.43-4.57 1.29+3.7+0.71+6.3
18.(21·22四年级下·黑龙江齐齐哈尔·期末)用简便方法计算。
53+238+347 37×99
76×237+237×24 698-(98+56)
19.(21·22四年级下·黑龙江绥化·期末)用简便方法计算。
99×0.625+0.625 8.59+2.57+3.43+6.41
421-175-25 3200÷25÷4
20.(21·22四年级下·黑龙江齐齐哈尔·期末)计算下面各题,能简算的写出必要的简算步骤。
83×101-83 16.03-8.64-1.36
120-6.9-3.1 128+167+172+33
350÷14×(276-254) 44×25
21.(21·22四年级下·黑龙江牡丹江·期末)脱式计算,能简算的要简算。
[192-(54+92)]×67 99×32+32 25×73×4
22.(21·22四年级下·黑龙江哈尔滨·期末)计算下面各题,怎样简便就怎样算。
640÷[8×(3.7+4.3)] 235-(456+304)÷4
101×53-53 48.76-(12.6+8.76) 125×25×32
23.(21·22四年级下·黑龙江七台河·期末)用简便方法计算下面各题。
75+168+25 672-36-64
99×38+38 72×125
24.(20·21四年级下·黑龙江牡丹江·期末)脱式计算。(能简算的要简算)
480÷[(69-24)÷9+11] 126×101-126 8000÷125÷8
五、解答题
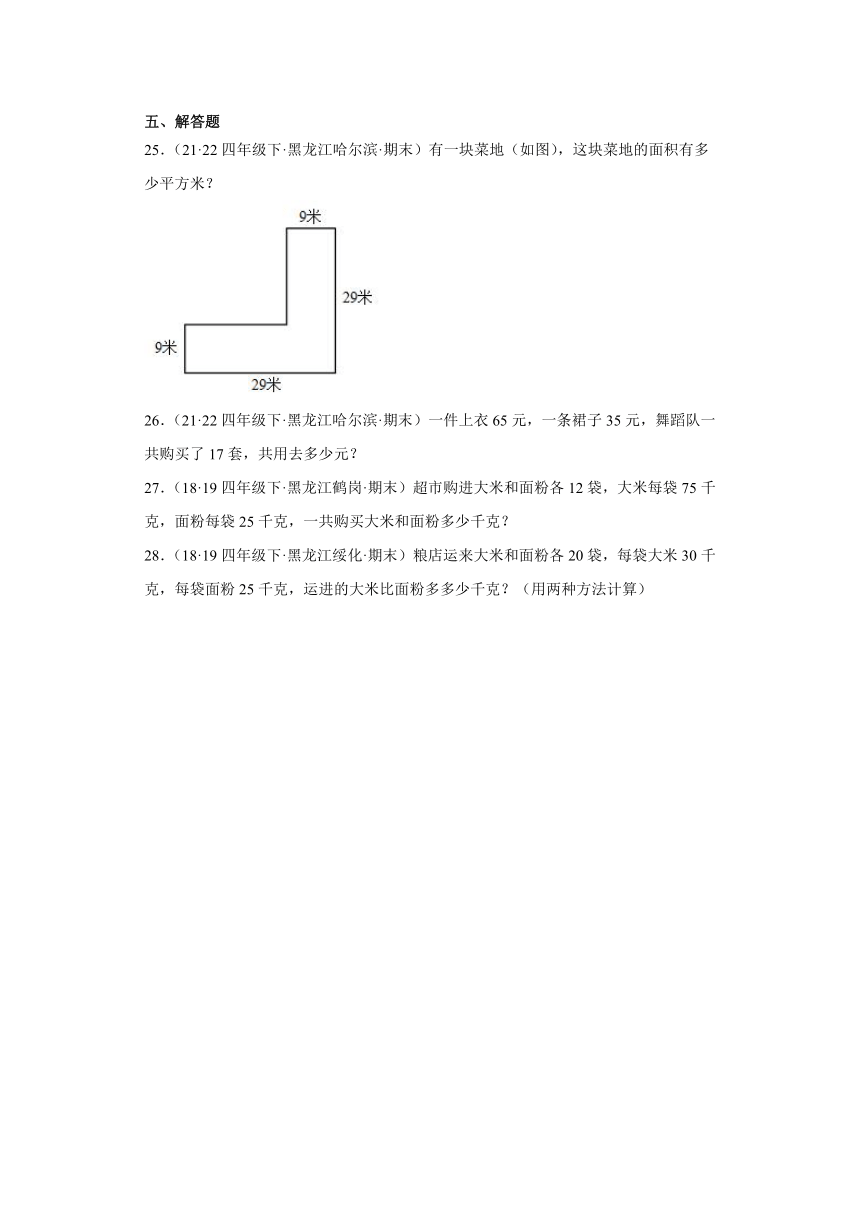
25.(21·22四年级下·黑龙江哈尔滨·期末)有一块菜地(如图),这块菜地的面积有多少平方米?
26.(21·22四年级下·黑龙江哈尔滨·期末)一件上衣65元,一条裙子35元,舞蹈队一共购买了17套,共用去多少元?
27.(18·19四年级下·黑龙江鹤岗·期末)超市购进大米和面粉各12袋,大米每袋75千克,面粉每袋25千克,一共购买大米和面粉多少千克?
28.(18·19四年级下·黑龙江绥化·期末)粮店运来大米和面粉各20袋,每袋大米30千克,每袋面粉25千克,运进的大米比面粉多多少千克?(用两种方法计算)
参考答案:
1.A
【分析】先将199写成99+100,然后再根据乘法分配律的特点进行判断即可,乘法分配律的特点是两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,依此比较。
【详解】99×99+199=99×99+99+100=99×(99+1)+100=99×100+100=100×(99+1)=100×100。
故答案为:A
【点睛】熟练掌握乘法分配律的特点是解答此题的关键。
2.B
【分析】本题把1002写成1000+2,再分别与88相乘,这样计算最简便,据此即可解答。
【详解】88×1002
=88×(1000+2)
=88×1000+88×2
=88000+176
=88176
故答案为:B
【点睛】本题主要考查学生对乘法分配律的掌握和灵活运用。
3.B
【分析】乘法结合律是指三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变。据此解答即可。
【详解】27×25×4=27×(25×4)运用了乘法结合律。
故答案为:B。
【点睛】乘法结合律是乘法运算中非常重要的定律,需熟练掌握,达到能认会用的地步。
4.B
【分析】根据题意,对各选项分别进行分析,进而得出结论。
【详解】A.195-45-55=195-(45+55),运用了减法的性质,所以计算正确,排除;
B.89×99=89×(100-1)=89×100-89≠89×100-1,应运用乘法的分配律进行简算,所以计算错误,符合题意;
C.125×106×8=125×8×106,运用了乘法交换律,所以计算正确,排除。
故答案为:B
【点睛】此题主要考查了学生对运算定律或运算性质的掌握情况。
5.B
【解析】将125和8放在一起,进行凑整,以达到简便计算的目的,调整了运算顺序,应用的是乘法结合律。
【详解】98×125×8=98×(125×8)依据的是乘法结合律;
故答案选:B。
【点睛】本题考查的是乘法结合律的应用,乘法结合律最显著的特点就是改变运算顺序。
6. 37 62 1
【分析】观察这个算式,其中42看成42×1,则这个算式是三个数分别和同一个数相乘,再把三个积相加,根据乘法分配律简算,可以先将三个数相加,再与这个数相乘。
【详解】42×37+42×62+42=42×(37+62+1)
【点睛】本题考查学生对乘法分配律的掌握情况。
7. 3 25 40
【分析】乘法分配律是指两个数的和同一个数相乘,等于把两个加数分别同这个数相乘,再把两个积加起来,结果不变。据此可知,计算25×97时,将97看成100-3。
乘法结合律是指三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变。据此可知,计算(13×25)×40,先算25×40。
【详解】25×97=25×(100-3) (13×25)×40=13×(25×40)
【点睛】本题考查乘法分配律和乘法结合律的认识和掌握情况。
8. 乘法交换 乘法结合
【分析】乘法交换律的特点是两个数相乘,交换两个因数的位置,积不变;乘法结合律的特点是三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变;依此填空。
【详解】8×49×125=49×(8×125)先交换了8与49的位置,因此8×49×125=49×(8×125)运用了乘法交换律和乘法结合律。
【点睛】熟练掌握乘法结合律和乘法交换律的特点是解答此题的关键。
9. 交换 结合
【分析】在4×73×25=73×(4×25)中,先把乘数4和73交换位置,因此先运用了乘法交换律,再把4与25结合,因此这里还运用了乘法结合律,据此解答即可。
【详解】4×73×25
=73×4×25
=73×(4×25)
=73×100
=7300
4×73×25=73×(4×25)运用了乘法的交换律和结合律。
【点睛】解决本题的关键是能够掌握各种运算定律的特点,并能够根据算式的特点选择合适的运算定律。
10. 加法结合律
【分析】加法结合律是指三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。用字母表示为:;据此解答。
【详解】〇△□〇△□,运用了加法结合律;用字母表示为:。
【点精】此题考查的目的是理解掌握加法结合律的意义及应用。
11.乘法分配
【解析】54×28+46×28写成(54+46)×28,是提取公因数28进行简便计算,相当于是乘法分配律的逆应用。
【详解】54×28+46×28=(54+46)×28运用了乘法分配律。
【点睛】乘法分配律是简便计算中应用最广泛的一条运算技巧,。
12. 4 5 a
【分析】有一个公因数a,那么可以根据乘法分配律的逆应用,提取公因数简便计算。
【详解】4×a+a×5=(4+5)×a
【点睛】本题考查的是乘法分配律,乘法分配律是简便计算中应用最广泛的一条运算技巧。
13. 42 4 25
【分析】乘法结合律:a×b×c=a×(b×c),据此即可解答。
【详解】42×4×25=42×(4×25)
【点睛】本题主要考查学生对乘法结合律的掌握和灵活运用。
14.×
【分析】乘法交换律是指两个数相乘,交换因数的位置,它们的积不变。据此可知,不能利用乘法交换律简算125×11+8,只能按照整数四则混合运算法则解答,先算乘法,再算加法。
【详解】125×11+8
=1375+8
=1383
则原算式计算错误。
故答案为:×
【点睛】本题考查学生对乘法交换律的认识和掌握情况。
15.×
【分析】乘法分配律:a×(b+c)=a×b+a×c,据此即可解答。
【详解】35×(100+2)=35×100+35×2,所以判断错误。
【点睛】本题主要考查学生对乘法分配律的掌握和灵活运用。
16.√
【解析】算式265×105-265×5中,有公因数265,那么可以根据乘法分配律的逆应用,提取公因数265简便计算。
【详解】265×105-265×5=265×(105-5)的变形是正确的;
题干阐述正确,故答案为:√。
【点睛】本题考查的是乘法分配律的应用,整数中学习的运算律,在随后小数、分数计算中同样适用。
17.2000;3300;8787
3.14;12
【分析】(1)根据乘法分配律进行简算。
(2)根据乘法交换律进行简算。
(3)将101看成100+1,再根据乘法分配律进行简算。
(4)根据减法的性质进行简算。
(5)根据加法交换律和加法结合律进行简算。
【详解】312×4+188×4
=(312+188)×4
=500×4
=2000
25×33×4
=25×4×33
=100×33
=3300
101×87
=(100+1)×87
=100×87+87
=8700+87
=8787
9.14-1.43-4.57
=9.14-(1.43+4.57)
=9.14-6
=3.14
1.29+3.7+0.71+6.3
=(1.29+0.71)+(3.7+6.3)
=2+10
=12
18.638;3663;
23700;544
【分析】(1)观察发现53和347相加可凑整,运用加法交换律简算即可;
(2)将99拆分为(100-1),再运用乘法分配律简算即可;
(3)运用乘法分配律简便计算即可;
(4)观察发现698和98相减可凑整,运用减法的性质去括号简算即可。
【详解】(1)53+238+347
=53+347+238
=400+238
=638
(2)37×99
=37×(100-1)
=37×100-37×1
=3700-37
=3663
(3)76×237+237×24
=(76+24)×237
=100×237
=23700
(4)698-(98+56)
=698-98-56
=600-56
=544
19.62.5;21;
221;32
【分析】运用乘法分配律进行计算;
运用小数加法交换律和加法结合律进行计算;
运用整数减法的性质进行计算;
运用整数除法的性质进行计算。
【详解】99×0.625+0.625
=(99+1)×0.625
=100×0.625
=62.5
8.59+2.57+3.43+6.41
=(8.59+6.41)+(2.57+3.43)
=15+6
=21
421-175-25
=421-(175+25)
=421-200
=221
3200÷25÷4
=3200÷(25×4)
=3200÷100
=32
20.8300;6.03
110;500;
550;1100
【分析】运用整数乘法分配律进行计算;
运用小数减法的性质进行计算;
运用小数减法的性质进行计算;
运用整数加法交换律和加法结合律进行计算;
先算小括号里面的减法,再算小括号外面的除法,最后算乘法;
运用乘法分配律进行计算。
【详解】83×101-83
=83×(101-1)
=83×100
=8300
16.03-8.64-1.36
=16.03-(8.64+1.36)
=16.03-10
=6.03
120-6.9-3.1
=120-(6.9+3.1)
=120-10
=110
128+167+172+33
=(128+172)+(167+33)
=300+200
=500
350÷14×(276-254)
=350÷14×22
=25×22
=550
44×25
=(40+4)×25
=40×25+4×25
=1000+100
=1100
21.3082;3200;7300
【分析】(1)先算小括号里面的加法,再算中括号里面的减法,最后算括号外面的乘法。
(2)根据乘法分配律进行简算。
(3)根据乘法交换律进行简算。
【详解】[192-(54+92)]×67
=[192-146]×67
=46×67
=3082
99×32+32
=(99+1)×32
=100×32
=3200
25×73×4
=25×4×73
=100×73
=7300
22.10;45
5300;27.4;100000
【分析】先算小括号里面的加法,再算中括号里面的乘法,最后算括号外的除法;
先算小括号里面的加法,再算括号外的除法,最后算括号外的减法;
根据乘法分配律简算;
根据减法的性质简算;
先把32分解成(4×8),再根据乘法交换律和结合律简算。
【详解】640÷[8×(3.7+4.3)]
=640÷[8×8]
=640÷64
=10
235-(456+304)÷4
=235-760÷4
=235-190
=45
101×53-53
=(101-1)×53
=100×53
=5300
48.76-(12.6+8.76)
=48.76-8.76-12.6
=40-12.6
=27.4
125×25×32
=125×25×(4×8)
=(125×8)×(25×4)
=1000×100
=100000
23.268;572;
3800;9000;
【分析】75+168+25此题先交换168与25的位置,然后再依次计算;
672-36-64此题运用减法的性质进行简算;
99×38+38此题运用乘法分配律的特点进行简算;
72×125此题将72写成9×8,然后运用乘法结合律的特点进行简算。
【详解】75+168+25
=75+25+168
=100+168
=268
672-36-64
=672-(36+64)
=672-100
=572
99×38+38
=(99+1)×38
=100×38
=3800
72×125
=9×8×125
=9×(8×125)
=9×1000
=9000
24.30;12600;8
【分析】(1)先算小括号里面的减法,再算中括号里面的除法,然后算中括号里面的加法,最后算括号外面的除法。
(2)根据乘法分配律进行简算。
(3)根据除法的性质进行简算。
【详解】480÷[(69-24)÷9+11]
=480÷[45÷9+11]
=480÷[5+11]
=480÷16
=30
126×101-126
=126×(101-1)
=126×100
=12600
8000÷125÷8
=8000÷(125×8)
=8000÷1000
=8
25.441平方米
【分析】根据这块地的特点,可以把它分割为两个长方形,根据长方形的面积=长×宽,把数据代入公式解答。
【详解】如图:
29×9+(29﹣9)×9
=29×9+20×9
=(29+20)×9
=49×9
=441(平方米)
答:这块菜地的面积有441平方米。
【点睛】此题主要考查长方形面积公式的灵活运用,关键是熟记公式。
26.1700元
【分析】先用65加上35求出每套的单价,再根据“单价×数量=总价”解答即可。
【详解】(65+35)×17
=100×17
=1700(元)
答:共用去1700元。
【点睛】解答此题也可以根据“单价×数量=总价”分别求出上衣和裙子的总价,然后再相加即可,列式为:65×17+35×17=1700(元)。
27.1200千克
【分析】用每袋大米的重量乘大米袋数,求出大米的重量。用每袋面粉的重量乘面粉袋数,求出面粉的重量。再将大米的重量加上面粉的重量解答。
【详解】75×12+25×12
=(75+25)×12
=100×12
=1200(千克)
答:一共购买大米和面粉1200千克。
【点睛】解决本题时先根据题意列出算式,再运用乘法分配律进行简算。
28.100千克
【解析】第一种方法,分别求出20袋大米和面粉各自的重量,相减得到大米比面粉多多少;第二种方法,先求出1袋大米比面粉多多少千克,再计算20袋大米比面粉多多少千克。
【详解】方法一:
20×30-20×25
=600-500
=100(千克)
方法二:
(30-25)×20
=5×20
=100(千克)
答:运进的大米比面粉多100千克。
【点睛】如果将两种方法综合起来看的话,相当于是,相当于是乘法分配律的应用。
一、选择题
1.(21·22四年级下·黑龙江绥化·期末)比较大小:99×99+199( )100×100。
A.= B.> C.<
2.(20·21四年级下·黑龙江牡丹江·期末)计算88×1002,最简便的算法是( )。
A.(90-2)×1002 B.88×(1000+2) C.80×1002+8×1002
3.(18·19四年级下·黑龙江鹤岗·期末)27×25×4=27×(25×4)运用了( )。
A.乘法交换律 B.乘法结合律 C.乖法分配律 D.乘法交换律与分配律
4.(17·18四年级下·黑龙江哈尔滨·期末)下列各式中,( )的计算是错误的。
A.195-45-55=195-(45+55) B.89×99=89×100-1 C.125×106×8=125×8×106
5.(17·18四年级下·黑龙江齐齐哈尔·期末)98×125×8﹦98×(125×8)这是根据( )。
A.乘法交换律 B.乘法结合律 C.乘法分配律
二、填空题
6.(21·22四年级下·黑龙江绥化·期末)42×37+42×62+42=42×( + + )
7.(21·22四年级下·黑龙江牡丹江·期末)在横线上填合适的数。
25×97=25×(100- ) (13×25)×40=13×( × )
8.(21·22四年级下·黑龙江七台河·期末)8×49×125=49×(8×125)运用了( )律和( )律。
9.(20·21四年级下·黑龙江牡丹江·期末)4×73×25=73×(4×25)运用了乘法的( )律和( )律。
10.(20·21四年级下·黑龙江七台河·期末)〇△□〇△□,运用了( ),用字母表示为( )。
11.(18·19四年级下·黑龙江绥化·期末)54×28+46×28=(54+46)×28这个算式运用了( )律。
12.(19·20四年级下·黑龙江鸡西·期末)4×a+a×5=( + )× 。
13.(19·20四年级下·黑龙江齐齐哈尔·期末)在横线上填上合适的数。
42×4×25= ×( × )
三、判断题
14.(21·22四年级下·黑龙江牡丹江·期末)125×11+8=125×8+11=1011。( )
15.(19·20四年级下·黑龙江齐齐哈尔·期末)35×(100+2)=35×100+2。( )
16.(19·20四年级下·黑龙江鸡西·期末)265×105-265×5=265×(105-5)。( )
四、计算题
17.(21·22四年级下·黑龙江绥化·期末)简算。
312×4+188×4 25×33×4 101×87
9.14-1.43-4.57 1.29+3.7+0.71+6.3
18.(21·22四年级下·黑龙江齐齐哈尔·期末)用简便方法计算。
53+238+347 37×99
76×237+237×24 698-(98+56)
19.(21·22四年级下·黑龙江绥化·期末)用简便方法计算。
99×0.625+0.625 8.59+2.57+3.43+6.41
421-175-25 3200÷25÷4
20.(21·22四年级下·黑龙江齐齐哈尔·期末)计算下面各题,能简算的写出必要的简算步骤。
83×101-83 16.03-8.64-1.36
120-6.9-3.1 128+167+172+33
350÷14×(276-254) 44×25
21.(21·22四年级下·黑龙江牡丹江·期末)脱式计算,能简算的要简算。
[192-(54+92)]×67 99×32+32 25×73×4
22.(21·22四年级下·黑龙江哈尔滨·期末)计算下面各题,怎样简便就怎样算。
640÷[8×(3.7+4.3)] 235-(456+304)÷4
101×53-53 48.76-(12.6+8.76) 125×25×32
23.(21·22四年级下·黑龙江七台河·期末)用简便方法计算下面各题。
75+168+25 672-36-64
99×38+38 72×125
24.(20·21四年级下·黑龙江牡丹江·期末)脱式计算。(能简算的要简算)
480÷[(69-24)÷9+11] 126×101-126 8000÷125÷8
五、解答题
25.(21·22四年级下·黑龙江哈尔滨·期末)有一块菜地(如图),这块菜地的面积有多少平方米?
26.(21·22四年级下·黑龙江哈尔滨·期末)一件上衣65元,一条裙子35元,舞蹈队一共购买了17套,共用去多少元?
27.(18·19四年级下·黑龙江鹤岗·期末)超市购进大米和面粉各12袋,大米每袋75千克,面粉每袋25千克,一共购买大米和面粉多少千克?
28.(18·19四年级下·黑龙江绥化·期末)粮店运来大米和面粉各20袋,每袋大米30千克,每袋面粉25千克,运进的大米比面粉多多少千克?(用两种方法计算)
参考答案:
1.A
【分析】先将199写成99+100,然后再根据乘法分配律的特点进行判断即可,乘法分配律的特点是两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,依此比较。
【详解】99×99+199=99×99+99+100=99×(99+1)+100=99×100+100=100×(99+1)=100×100。
故答案为:A
【点睛】熟练掌握乘法分配律的特点是解答此题的关键。
2.B
【分析】本题把1002写成1000+2,再分别与88相乘,这样计算最简便,据此即可解答。
【详解】88×1002
=88×(1000+2)
=88×1000+88×2
=88000+176
=88176
故答案为:B
【点睛】本题主要考查学生对乘法分配律的掌握和灵活运用。
3.B
【分析】乘法结合律是指三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变。据此解答即可。
【详解】27×25×4=27×(25×4)运用了乘法结合律。
故答案为:B。
【点睛】乘法结合律是乘法运算中非常重要的定律,需熟练掌握,达到能认会用的地步。
4.B
【分析】根据题意,对各选项分别进行分析,进而得出结论。
【详解】A.195-45-55=195-(45+55),运用了减法的性质,所以计算正确,排除;
B.89×99=89×(100-1)=89×100-89≠89×100-1,应运用乘法的分配律进行简算,所以计算错误,符合题意;
C.125×106×8=125×8×106,运用了乘法交换律,所以计算正确,排除。
故答案为:B
【点睛】此题主要考查了学生对运算定律或运算性质的掌握情况。
5.B
【解析】将125和8放在一起,进行凑整,以达到简便计算的目的,调整了运算顺序,应用的是乘法结合律。
【详解】98×125×8=98×(125×8)依据的是乘法结合律;
故答案选:B。
【点睛】本题考查的是乘法结合律的应用,乘法结合律最显著的特点就是改变运算顺序。
6. 37 62 1
【分析】观察这个算式,其中42看成42×1,则这个算式是三个数分别和同一个数相乘,再把三个积相加,根据乘法分配律简算,可以先将三个数相加,再与这个数相乘。
【详解】42×37+42×62+42=42×(37+62+1)
【点睛】本题考查学生对乘法分配律的掌握情况。
7. 3 25 40
【分析】乘法分配律是指两个数的和同一个数相乘,等于把两个加数分别同这个数相乘,再把两个积加起来,结果不变。据此可知,计算25×97时,将97看成100-3。
乘法结合律是指三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变。据此可知,计算(13×25)×40,先算25×40。
【详解】25×97=25×(100-3) (13×25)×40=13×(25×40)
【点睛】本题考查乘法分配律和乘法结合律的认识和掌握情况。
8. 乘法交换 乘法结合
【分析】乘法交换律的特点是两个数相乘,交换两个因数的位置,积不变;乘法结合律的特点是三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变;依此填空。
【详解】8×49×125=49×(8×125)先交换了8与49的位置,因此8×49×125=49×(8×125)运用了乘法交换律和乘法结合律。
【点睛】熟练掌握乘法结合律和乘法交换律的特点是解答此题的关键。
9. 交换 结合
【分析】在4×73×25=73×(4×25)中,先把乘数4和73交换位置,因此先运用了乘法交换律,再把4与25结合,因此这里还运用了乘法结合律,据此解答即可。
【详解】4×73×25
=73×4×25
=73×(4×25)
=73×100
=7300
4×73×25=73×(4×25)运用了乘法的交换律和结合律。
【点睛】解决本题的关键是能够掌握各种运算定律的特点,并能够根据算式的特点选择合适的运算定律。
10. 加法结合律
【分析】加法结合律是指三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。用字母表示为:;据此解答。
【详解】〇△□〇△□,运用了加法结合律;用字母表示为:。
【点精】此题考查的目的是理解掌握加法结合律的意义及应用。
11.乘法分配
【解析】54×28+46×28写成(54+46)×28,是提取公因数28进行简便计算,相当于是乘法分配律的逆应用。
【详解】54×28+46×28=(54+46)×28运用了乘法分配律。
【点睛】乘法分配律是简便计算中应用最广泛的一条运算技巧,。
12. 4 5 a
【分析】有一个公因数a,那么可以根据乘法分配律的逆应用,提取公因数简便计算。
【详解】4×a+a×5=(4+5)×a
【点睛】本题考查的是乘法分配律,乘法分配律是简便计算中应用最广泛的一条运算技巧。
13. 42 4 25
【分析】乘法结合律:a×b×c=a×(b×c),据此即可解答。
【详解】42×4×25=42×(4×25)
【点睛】本题主要考查学生对乘法结合律的掌握和灵活运用。
14.×
【分析】乘法交换律是指两个数相乘,交换因数的位置,它们的积不变。据此可知,不能利用乘法交换律简算125×11+8,只能按照整数四则混合运算法则解答,先算乘法,再算加法。
【详解】125×11+8
=1375+8
=1383
则原算式计算错误。
故答案为:×
【点睛】本题考查学生对乘法交换律的认识和掌握情况。
15.×
【分析】乘法分配律:a×(b+c)=a×b+a×c,据此即可解答。
【详解】35×(100+2)=35×100+35×2,所以判断错误。
【点睛】本题主要考查学生对乘法分配律的掌握和灵活运用。
16.√
【解析】算式265×105-265×5中,有公因数265,那么可以根据乘法分配律的逆应用,提取公因数265简便计算。
【详解】265×105-265×5=265×(105-5)的变形是正确的;
题干阐述正确,故答案为:√。
【点睛】本题考查的是乘法分配律的应用,整数中学习的运算律,在随后小数、分数计算中同样适用。
17.2000;3300;8787
3.14;12
【分析】(1)根据乘法分配律进行简算。
(2)根据乘法交换律进行简算。
(3)将101看成100+1,再根据乘法分配律进行简算。
(4)根据减法的性质进行简算。
(5)根据加法交换律和加法结合律进行简算。
【详解】312×4+188×4
=(312+188)×4
=500×4
=2000
25×33×4
=25×4×33
=100×33
=3300
101×87
=(100+1)×87
=100×87+87
=8700+87
=8787
9.14-1.43-4.57
=9.14-(1.43+4.57)
=9.14-6
=3.14
1.29+3.7+0.71+6.3
=(1.29+0.71)+(3.7+6.3)
=2+10
=12
18.638;3663;
23700;544
【分析】(1)观察发现53和347相加可凑整,运用加法交换律简算即可;
(2)将99拆分为(100-1),再运用乘法分配律简算即可;
(3)运用乘法分配律简便计算即可;
(4)观察发现698和98相减可凑整,运用减法的性质去括号简算即可。
【详解】(1)53+238+347
=53+347+238
=400+238
=638
(2)37×99
=37×(100-1)
=37×100-37×1
=3700-37
=3663
(3)76×237+237×24
=(76+24)×237
=100×237
=23700
(4)698-(98+56)
=698-98-56
=600-56
=544
19.62.5;21;
221;32
【分析】运用乘法分配律进行计算;
运用小数加法交换律和加法结合律进行计算;
运用整数减法的性质进行计算;
运用整数除法的性质进行计算。
【详解】99×0.625+0.625
=(99+1)×0.625
=100×0.625
=62.5
8.59+2.57+3.43+6.41
=(8.59+6.41)+(2.57+3.43)
=15+6
=21
421-175-25
=421-(175+25)
=421-200
=221
3200÷25÷4
=3200÷(25×4)
=3200÷100
=32
20.8300;6.03
110;500;
550;1100
【分析】运用整数乘法分配律进行计算;
运用小数减法的性质进行计算;
运用小数减法的性质进行计算;
运用整数加法交换律和加法结合律进行计算;
先算小括号里面的减法,再算小括号外面的除法,最后算乘法;
运用乘法分配律进行计算。
【详解】83×101-83
=83×(101-1)
=83×100
=8300
16.03-8.64-1.36
=16.03-(8.64+1.36)
=16.03-10
=6.03
120-6.9-3.1
=120-(6.9+3.1)
=120-10
=110
128+167+172+33
=(128+172)+(167+33)
=300+200
=500
350÷14×(276-254)
=350÷14×22
=25×22
=550
44×25
=(40+4)×25
=40×25+4×25
=1000+100
=1100
21.3082;3200;7300
【分析】(1)先算小括号里面的加法,再算中括号里面的减法,最后算括号外面的乘法。
(2)根据乘法分配律进行简算。
(3)根据乘法交换律进行简算。
【详解】[192-(54+92)]×67
=[192-146]×67
=46×67
=3082
99×32+32
=(99+1)×32
=100×32
=3200
25×73×4
=25×4×73
=100×73
=7300
22.10;45
5300;27.4;100000
【分析】先算小括号里面的加法,再算中括号里面的乘法,最后算括号外的除法;
先算小括号里面的加法,再算括号外的除法,最后算括号外的减法;
根据乘法分配律简算;
根据减法的性质简算;
先把32分解成(4×8),再根据乘法交换律和结合律简算。
【详解】640÷[8×(3.7+4.3)]
=640÷[8×8]
=640÷64
=10
235-(456+304)÷4
=235-760÷4
=235-190
=45
101×53-53
=(101-1)×53
=100×53
=5300
48.76-(12.6+8.76)
=48.76-8.76-12.6
=40-12.6
=27.4
125×25×32
=125×25×(4×8)
=(125×8)×(25×4)
=1000×100
=100000
23.268;572;
3800;9000;
【分析】75+168+25此题先交换168与25的位置,然后再依次计算;
672-36-64此题运用减法的性质进行简算;
99×38+38此题运用乘法分配律的特点进行简算;
72×125此题将72写成9×8,然后运用乘法结合律的特点进行简算。
【详解】75+168+25
=75+25+168
=100+168
=268
672-36-64
=672-(36+64)
=672-100
=572
99×38+38
=(99+1)×38
=100×38
=3800
72×125
=9×8×125
=9×(8×125)
=9×1000
=9000
24.30;12600;8
【分析】(1)先算小括号里面的减法,再算中括号里面的除法,然后算中括号里面的加法,最后算括号外面的除法。
(2)根据乘法分配律进行简算。
(3)根据除法的性质进行简算。
【详解】480÷[(69-24)÷9+11]
=480÷[45÷9+11]
=480÷[5+11]
=480÷16
=30
126×101-126
=126×(101-1)
=126×100
=12600
8000÷125÷8
=8000÷(125×8)
=8000÷1000
=8
25.441平方米
【分析】根据这块地的特点,可以把它分割为两个长方形,根据长方形的面积=长×宽,把数据代入公式解答。
【详解】如图:
29×9+(29﹣9)×9
=29×9+20×9
=(29+20)×9
=49×9
=441(平方米)
答:这块菜地的面积有441平方米。
【点睛】此题主要考查长方形面积公式的灵活运用,关键是熟记公式。
26.1700元
【分析】先用65加上35求出每套的单价,再根据“单价×数量=总价”解答即可。
【详解】(65+35)×17
=100×17
=1700(元)
答:共用去1700元。
【点睛】解答此题也可以根据“单价×数量=总价”分别求出上衣和裙子的总价,然后再相加即可,列式为:65×17+35×17=1700(元)。
27.1200千克
【分析】用每袋大米的重量乘大米袋数,求出大米的重量。用每袋面粉的重量乘面粉袋数,求出面粉的重量。再将大米的重量加上面粉的重量解答。
【详解】75×12+25×12
=(75+25)×12
=100×12
=1200(千克)
答:一共购买大米和面粉1200千克。
【点睛】解决本题时先根据题意列出算式,再运用乘法分配律进行简算。
28.100千克
【解析】第一种方法,分别求出20袋大米和面粉各自的重量,相减得到大米比面粉多多少;第二种方法,先求出1袋大米比面粉多多少千克,再计算20袋大米比面粉多多少千克。
【详解】方法一:
20×30-20×25
=600-500
=100(千克)
方法二:
(30-25)×20
=5×20
=100(千克)
答:运进的大米比面粉多100千克。
【点睛】如果将两种方法综合起来看的话,相当于是,相当于是乘法分配律的应用。
