数学人教A版(2019)必修第二册10.1.2事件的关系和运算 课件(共23张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册10.1.2事件的关系和运算 课件(共23张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
第十章《概率》人教A版2019必修第二册10.1.2 事件的关系和运算1.了解事件间的相互关系与运算
2.理解互斥事件、对立事件的概念
学习目标
从前面的学习中可以看到,我们在一个随机试验中可以定义很多随机事件.这些事件有的简单,有的复杂.我们希望从简单事件的概率推算出复杂事件的概率,所以需要研究事件之间的关系和运算.
环节一:创设情境,引入课题
事实上,利用样本空间的子集表示事件,使我们可以利用集合的知识研究随机事件,从而为研究概率的性质和计算等提供有效而简便的方法.下面我们按照这一思路展开研究.
环节二:观察分析,感知概念
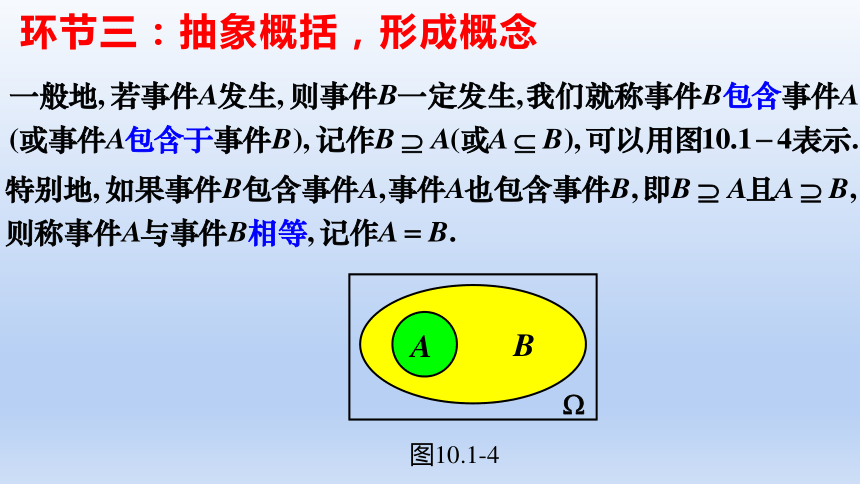
B
图10.1-4
A
环节三:抽象概括,形成概念
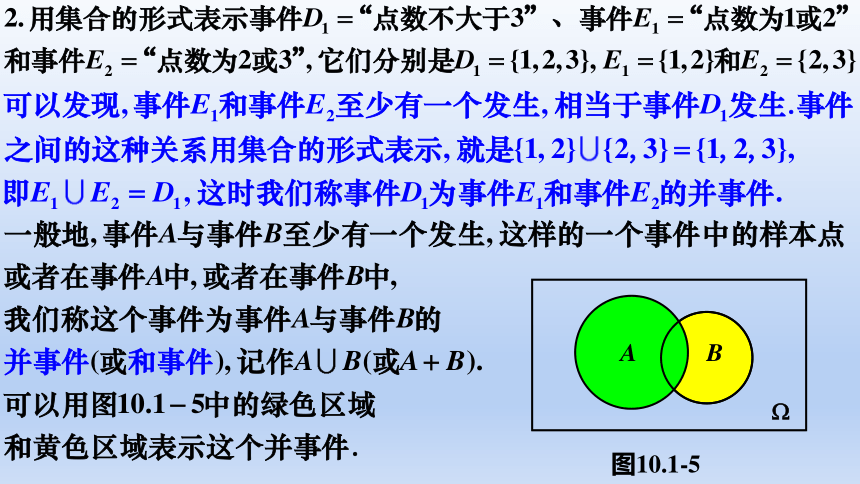
B
A
图10.1-5
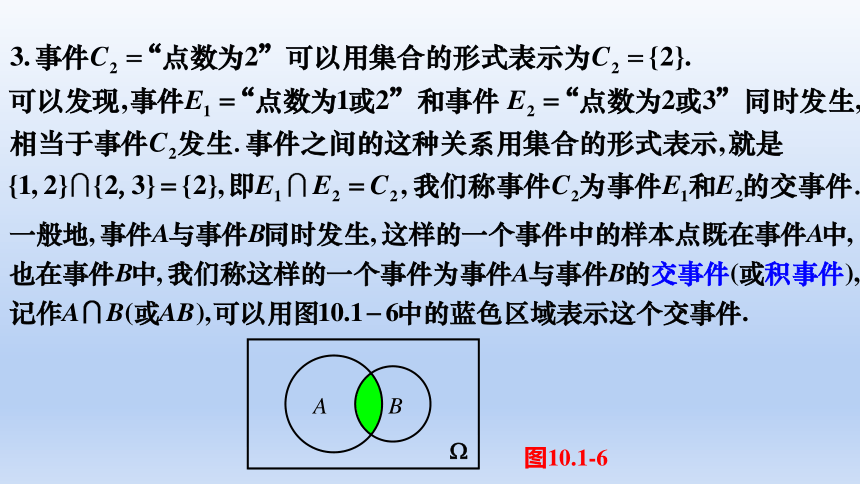
图10.1-6
A
B
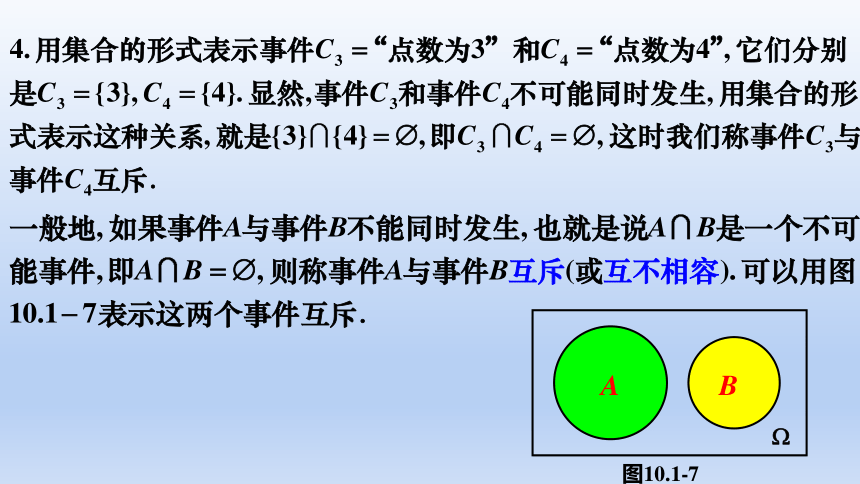
A
B
图10.1-7
A
图10.1-8
环节四:辨析理解,深化概念
综上所述,事件的关系或运算的含义,以及相应的符号表示如下(表10.1-1):
表10.1-1
事件的关系或运算 含义 符号表示
包含 A发生导致B发生
并事件(和事件) A 与B至少一个发生
交事件(积事件) A与B同时发生
互斥(互不相容) A 与B不能同时发生
互为对立 A 与B有且仅有一个发生
环节五:课堂练习,巩固运用
1
2
1
2
1
4
1
2
1
3
1
4
2
1
2
3
2
4
3
1
3
2
3
4
4
1
4
2
4
3
图10.1-10
1
2
1
2
1
4
1
2
1
3
1
4
2
1
2
3
2
4
3
1
3
2
3
4
4
1
4
2
4
3
图10.1-10
1.事件的各种关系与运算,可以类比集合的关系与运算,互斥事件与对立事件的概念的外延具有包含关系,即{对立事件} {互斥事件}.
2.在一次试验中,两个互斥事件不能同时发生,它包括一个事件发生而另一个事件不发生,或者两个事件都不发生,两个对立事件有且仅有一个发生.
3.事件(A+B)或(A∪B),表示事件A与事件B至少有一个发生,事件(AB)或A∩B,表示事件A与事件B同时发生.
环节六:归纳总结,反思提升
4.包含关系、相等关系的判定
①事件的包含关系与集合的包含关系相似;
②两事件相等的实质为相同事件,即同时发生或同时不发生.
5.判断事件是否互斥的两个步骤
第一步,确定每个事件包含的结果;
第二步,确定是否有一个结果发生会意味着两个事件都发生,若是,则两个事件不互斥,否则就是互斥的.
6.判断事件是否对立的两个步骤
第一步,判断是互斥事件;
第二步,确定两个事件必然有一个发生,否则只有互斥,但不对立.
环节七:目标检测,作业布置
完成教材:第233页 练习1,2题
第243页 习题10.1的15题.
练习(第233页)
1.某人打靶时连续射击两次,下列事件中与事件“至少一次中靶”互为对立的是( )
(A)至多一次中靶 (B)两次都中靶
(C)只有一次中靶 (D)两次都没有中靶
“至少一次中靶”表示两次射击中一次中靶,另一次没中靶或两次都中靶,其对立事件为两次都没有中靶.故选D.
D
正确
错误
正确
正确
正确
正确
正确
正确
正确
正确
第十章《概率》人教A版2019必修第二册10.1.2 事件的关系和运算1.了解事件间的相互关系与运算
2.理解互斥事件、对立事件的概念
学习目标
从前面的学习中可以看到,我们在一个随机试验中可以定义很多随机事件.这些事件有的简单,有的复杂.我们希望从简单事件的概率推算出复杂事件的概率,所以需要研究事件之间的关系和运算.
环节一:创设情境,引入课题
事实上,利用样本空间的子集表示事件,使我们可以利用集合的知识研究随机事件,从而为研究概率的性质和计算等提供有效而简便的方法.下面我们按照这一思路展开研究.
环节二:观察分析,感知概念
B
图10.1-4
A
环节三:抽象概括,形成概念
B
A
图10.1-5
图10.1-6
A
B
A
B
图10.1-7
A
图10.1-8
环节四:辨析理解,深化概念
综上所述,事件的关系或运算的含义,以及相应的符号表示如下(表10.1-1):
表10.1-1
事件的关系或运算 含义 符号表示
包含 A发生导致B发生
并事件(和事件) A 与B至少一个发生
交事件(积事件) A与B同时发生
互斥(互不相容) A 与B不能同时发生
互为对立 A 与B有且仅有一个发生
环节五:课堂练习,巩固运用
1
2
1
2
1
4
1
2
1
3
1
4
2
1
2
3
2
4
3
1
3
2
3
4
4
1
4
2
4
3
图10.1-10
1
2
1
2
1
4
1
2
1
3
1
4
2
1
2
3
2
4
3
1
3
2
3
4
4
1
4
2
4
3
图10.1-10
1.事件的各种关系与运算,可以类比集合的关系与运算,互斥事件与对立事件的概念的外延具有包含关系,即{对立事件} {互斥事件}.
2.在一次试验中,两个互斥事件不能同时发生,它包括一个事件发生而另一个事件不发生,或者两个事件都不发生,两个对立事件有且仅有一个发生.
3.事件(A+B)或(A∪B),表示事件A与事件B至少有一个发生,事件(AB)或A∩B,表示事件A与事件B同时发生.
环节六:归纳总结,反思提升
4.包含关系、相等关系的判定
①事件的包含关系与集合的包含关系相似;
②两事件相等的实质为相同事件,即同时发生或同时不发生.
5.判断事件是否互斥的两个步骤
第一步,确定每个事件包含的结果;
第二步,确定是否有一个结果发生会意味着两个事件都发生,若是,则两个事件不互斥,否则就是互斥的.
6.判断事件是否对立的两个步骤
第一步,判断是互斥事件;
第二步,确定两个事件必然有一个发生,否则只有互斥,但不对立.
环节七:目标检测,作业布置
完成教材:第233页 练习1,2题
第243页 习题10.1的15题.
练习(第233页)
1.某人打靶时连续射击两次,下列事件中与事件“至少一次中靶”互为对立的是( )
(A)至多一次中靶 (B)两次都中靶
(C)只有一次中靶 (D)两次都没有中靶
“至少一次中靶”表示两次射击中一次中靶,另一次没中靶或两次都中靶,其对立事件为两次都没有中靶.故选D.
D
正确
错误
正确
正确
正确
正确
正确
正确
正确
正确
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
