2024年中考物理一轮复习考点梳理学案 第23讲 简单机械(含解析)
文档属性
| 名称 | 2024年中考物理一轮复习考点梳理学案 第23讲 简单机械(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-03-14 13:46:13 | ||
图片预览



文档简介
第23讲 简单机械
命题分析
广东省近五年中考物理命题分析
考点 2023 2022 2021 2020 2019
杠杆 省题16、21 省题17 省题20 省题15 省题15
滑轮 ___ 省题6 省题14 省题14 省题19
机械效率 ___ ___ ___ ___ ___
【课程标准】
2.2.6 知道简单机械。探究并了解杠杆的平衡条件。
3.2.3 知道机械效率。了解提高机械效率的意义和途径。
例 测量某种简单机械的机械效率。
3.2.4 能说出人类使用的一些机械。了解机械的使用对社会发展的作用。
4.2.5 探究杠杆的平衡条件。
例 用杠杆、铁架台、钩码和弹簧测力计,探究杠杆平衡时动力、动力臂与阻力、阻力臂之间的定量关系。
考点一 杠杆
一、认识杠杆
1.定义:一根硬棒,在力的作用下能绕着固定点O转动,这根硬棒就是杠杆。
2.关于杠杆的名词
(1)支点:杠杆可以绕其转动的点O。
(2)动力:使杠杆转动的力F1。
(3)阻力:阻碍杠杆转动的力F2。
(4)动力臂:从支点到动力F1作用线的距离l1。
(5)阻力臂:从支点到阻力F2作用线的距离l2。
3.杠杆的平衡条件:动力×动力臂=阻力×阻力臂,或写为F1l1=F2l2。
注意:计算时,动力F1和阻力F2单位要统一,动力臂l1和阻力臂l2单位也要统一。
二、杠杆应用
种类 省力杠杆 费力杠杆 等臂杠杆
图例
力臂关系 l1>l2 l1<l2 l1=l2
力的关系 F1<F2 F1>F2 F1=F2
特点 省力费距离 省距离费力 既不省力也不费距离
实例 钢丝钳 钓鱼竿 天平
(1)杠杆一定是直的。( × )
(2)支点一定在杠杆上。( √ )
(3)力臂是杠杆的支点到力的作用点的距离。( × )
(4)同一个杠杆,动力臂和阻力臂的长度是不变的,与动力和阻力的方向无关。( × )
(5)只要设计合理,同一杠杆既可以省力也可以省距离。( × )
(6)能够省力的杠杆,一定费距离。( √ )
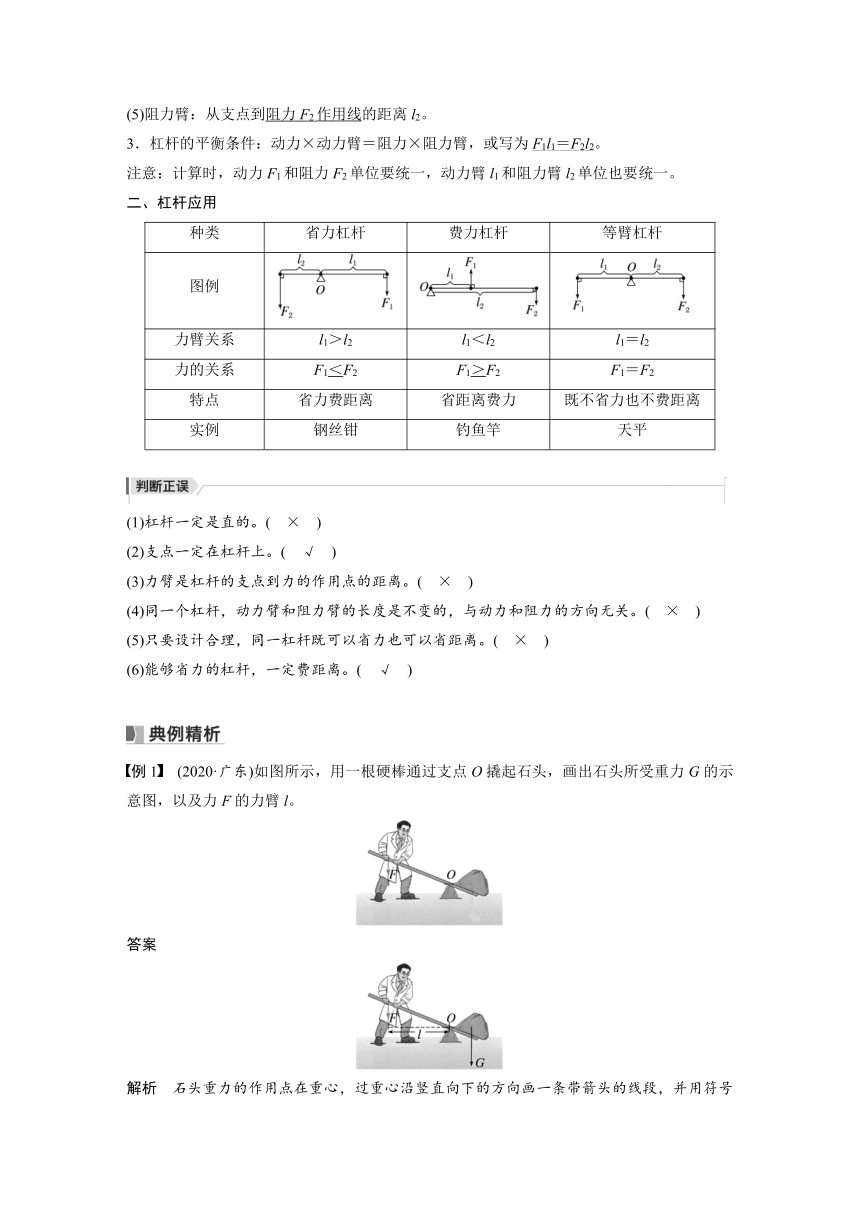
例1 (2020·广东)如图所示,用一根硬棒通过支点O撬起石头,画出石头所受重力G的示意图,以及力F的力臂l。
答案
解析 石头重力的作用点在重心,过重心沿竖直向下的方向画一条带箭头的线段,并用符号G表示;过支点O作垂直于动力作用线的垂线段,即为F的力臂l。
例2 (2023·广州越秀区模拟)如图,重力为G、质量分布均匀的木棒左端与支点O连接,绕O转动时,棒所受的摩擦力可忽略不计。棒重心处受到竖直向上的拉力F1保持静止,则( )
A.F1=G
B.F1·OA=G·OB
C.若F1为杠杆的动力,G为杠杆的阻力,此杠杆为费力杠杆
D.若将竖直拉力移到C点棒仍静止,此时拉力记为F2,则F1<F2
答案 A
解析 由题图可知,竖直向上的拉力F1作用在棒重心处,力臂为OB,因为木棒质量分布均匀,则杠杆自身重力的力臂也为OB,若F1为杠杆的动力,G为杠杆的阻力,根据杠杆平衡条件可知,F1·OB=G·OB,由F1=G,此时动力和阻力大小相同,是一个等臂杠杆,故A正确,B、C错误;若将竖直拉力移到C点,棒仍静止且大小为F2,此时F2的力臂相比F1的力臂变长,杠杆自身重力不变,重力的力臂不变,根据杠杆平衡条件可知,拉力F2变小,则F1>F2,故D错误。
名师点拨 (1)凡省力的杠杆必定费距离,凡省距离的杠杆必定费力。 (2)判断杠杆的种类,主要通过动力臂和阻力臂的大小进行判断,对于一些不容易判断力臂大小的杠杆,可根据使用杠杆的目的(是省距离还是省力)来判断,如用筷子吃饭时省距离,则筷子为费力杠杆。
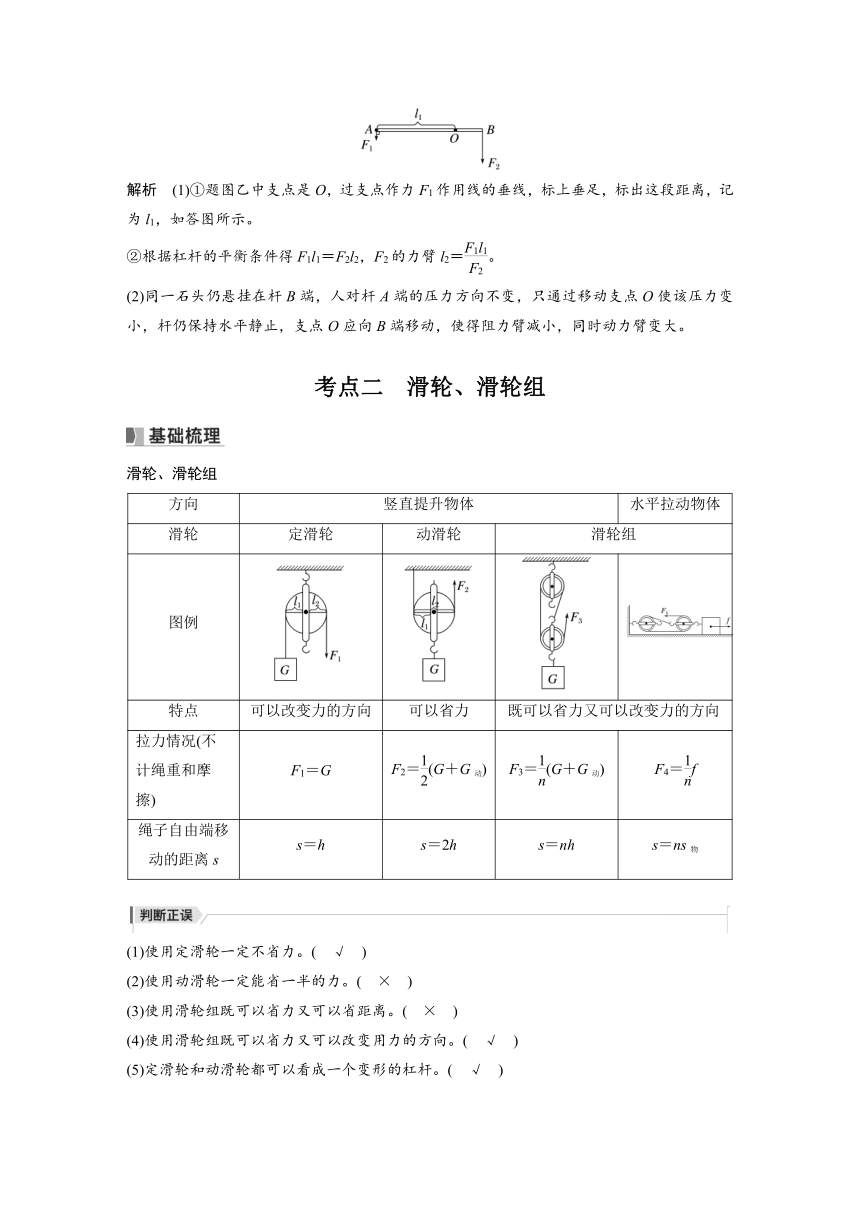
例3 (2023·广州)图甲中工人用工具搬运石头,该工具可简化成图乙中杠杆AB,移动支架,可使支点O在AB间移动。杆水平静止,忽略杆重。
(1)人对杆的压力为F1,绳对杆的拉力为F2,F1、F2竖直向下。
①在图乙中画出F1的力臂l1;
②F2的力臂l2=________(用F1、F2、l1表示)。
(2)同一石头仍悬挂在杆B端,人对杆A端的压力方向不变,只通过移动支点O使该压力变小,杆仍保持水平静止,支点O应向________(选填“A”或“B”)端移动。
答案 (1)①如图所示 ② (2)B
解析 (1)①题图乙中支点是O,过支点作力F1作用线的垂线,标上垂足,标出这段距离,记为l1,如答图所示。
②根据杠杆的平衡条件得F1l1=F2l2,F2的力臂l2=。
(2)同一石头仍悬挂在杆B端,人对杆A端的压力方向不变,只通过移动支点O使该压力变小,杆仍保持水平静止,支点O应向B端移动,使得阻力臂减小,同时动力臂变大。
考点二 滑轮、滑轮组
滑轮、滑轮组
方向 竖直提升物体 水平拉动物体
滑轮 定滑轮 动滑轮 滑轮组
图例
特点 可以改变力的方向 可以省力 既可以省力又可以改变力的方向
拉力情况(不计绳重和摩擦) F1=G F2=(G+G动) F3=(G+G动) F4=f
绳子自由端移动的距离s s=h s=2h s=nh s=ns物
(1)使用定滑轮一定不省力。( √ )
(2)使用动滑轮一定能省一半的力。( × )
(3)使用滑轮组既可以省力又可以省距离。( × )
(4)使用滑轮组既可以省力又可以改变用力的方向。( √ )
(5)定滑轮和动滑轮都可以看成一个变形的杠杆。( √ )
例4 (2023·重庆)在美丽乡村建设的工地上,如图所示,工人借助动滑轮用250 N的拉力,将450 N的重物匀速提升2 m,用时10 s。则( )
A.重物上升的速度为0.4 m/s B.动滑轮做的有用功为1 000 J
C.工人的拉力的功率为90 W D.拉力做的总功1 000 J
答案 D
解析 重物上升的速度v===0.2 m/s,故A错误;动滑轮做的有用功W有=Gh=450 N×2 m=900 J,故B错误;由题图可知,绳子自由端移动的距离s=nh=2×2 m=4 m,拉力做的总功W总=Fs=250 N×4 m=1 000 J,拉力做功的功率P===100 W,故C错误,D正确。
例5 (2023·肇庆怀集县一模)如图所示,小明同学想把被台风刮倒的甲树拉正,他把绳子的一端系在乙树上,然后绕过甲树用力拉绳子,这样做时甲树干相当于________(选填“动滑轮”“定滑轮”或“杠杆”)。如果不计绳重和摩擦,甲树受到500 N拉力,则小明对绳子的拉力为________ N,乙树受到的拉力为________ N。
答案 动滑轮 250 250
解析 把绳子的一端系在乙树上,然后绕过甲树用力拉绳子时,甲树干要移动,则甲树干相当于动滑轮;拉甲树干的绳子段数是2,不计绳重和摩擦,所以小明对绳子的拉力F=×500 N=250 N,乙树受到的拉力等于1段绳子的拉力,大小为250 N。
考点三 机械效率
1.机械效率定义:有用功跟总功的比值。
用公式表示η=。
2.使用机械时,有用功总是小于总功,机械效率总是小于1,机械效率通常用百分数表示。
3.常见简单机械的机械效率
简单机械 定滑轮 动滑轮、滑轮组 斜面
图例
有用功 W有=Gh W有=Gh W有=Gh
总功 W总=Fs W总=Fs W总=Fs
机械效率 η= η=== η==
(1)同一个滑轮组,其机械效率是固定不变的。( × )
(2)功率大的机械,机械效率一定高。( × )
(3)越省力的机械,机械效率越高。( × )
(4)所做有用功越多的机械,机械效率越高。( × )
(5)做功相等的情况下,额外功越少的机械,机械效率越高。( √ )
例6 (2023·佛山禅城区一模)如图所示,用两个完全相同的滑轮匀速提升所受重力相等的物体。不计轴处摩擦,比较甲、乙装置可知( )
A.甲省力,机械效率较高
B.甲不省力,机械效率较低
C.乙省力,机械效率较低
D.乙不省力,机械效率较高
答案 D
解析 定滑轮不省力,不用对滑轮做功,故机械效率高;动滑轮省力,但要对滑轮做额外功,故机械效率低,故选D。
例7 (2023·惠州一模)如图所示,把重为200 N的物体匀速提升2 m,不计滑轮、绳子的重力及摩擦,所用拉力F为________ N,拉力所做的功为________ J;若拉力为110 N,滑轮组的机械效率为________。
答案 100 400 90.9%
解析 由滑轮组可知,承重绳子的有效股数n=2,
拉力F===100 N;
绳子自由端移动的距离s=nh=2×2 m=4 m,
拉力做的功W=Fs=100 N×4 m=400 J;
若拉力为110 N,
由滑轮组的机械效率公式可知滑轮组的机械效率η===90.9%。
实验一 探究杠杆的平衡条件
实验器材 铁架台、杠杆、钩码、细绳。
实验步骤 (1)将杠杆固定在铁架台上,调节杠杆两端的平衡螺母,使杠杆在水平位置保持平衡;
(2)给杠杆两侧挂钩码,移动钩码的位置,使杠杆重新在水平位置平衡,读出平衡时动力、动力臂、阻力、阻力臂的数值填入表格中;
(3)改变动力、动力臂的大小,相应调节阻力、阻力臂,再重复做几次实验。
实验结论 动力×动力臂=阻力×阻力臂(或F1l1=F2l2)。
例8 小明在“探究杠杆平衡条件”的实验中,采用了如图甲所示的实验装置(实验中所用钩码均相同,杠杆质量均匀,相邻刻度线之间的距离相等)。
[实验设计与进行]
(1)实验前杠杆左端高、右端低,此时杠杆处于________(选填“平衡”或“非平衡”)状态。接下来应将杠杆左端的平衡螺母向________(选填“左”或“右”,下同)调节,或将杠杆右端的平衡螺母向______调节,使杠杆处于水平静止状态。
(2)图乙中杠杆恰好处于水平位置平衡,小明尝试在A点下方再加挂2个相同的钩码,则杠杆______(选填“左”或“右”)端会下沉,为使杠杆保持水平平衡,他可以将挂在B点的钩码________________(填具体操作)。
(3)小明又尝试用弹簧测力计代替B点悬挂的钩码,并始终竖直向下拉弹簧测力计,使杠杆从水平位置缓慢转过一定角度,如图丙所示。此过程中弹簧测力计的示数会________(选填“变大”“变小”或“不变”)。(不计阻力影响)
[拓展设问]
(4)小刚同学用图丁所示的装置进行探究,发现当杠杆水平平衡时,与小明同学得出的杠杆平衡条件不相符,其可能的原因是____________________________________________。
(5)小刚同学如果改为倾斜拉弹簧测力计,杠杆还是平衡,弹簧测力计的示数________(选填“变大”“变小”或“不变”)。
(6)小刚用丁图的装置测杠杆的机械效率,若把弹簧测力计由A点移到B点,仍将钩码提升相同的高度,则杠杆的机械效率将________(选填“变大”“变小”或“不变”)。
答案 (1)平衡 左 左 (2)左 向右移动2格 (3)不变 (4)杠杆的重力对杠杆转动产生了影响 (5)变大 (6)不变
解析 (1)杠杆静止时处于平衡状态;杠杆右端下沉,为了使杠杆在水平位置平衡,则他应将杠杆左端的平衡螺母向左调节,或将杠杆右端的平衡螺母向左调节。
(2)设杠杆的一个小格为L,一个钩码重为G,小明尝试在A点下方再加挂2个相同的钩码,(3G+2G)×2L>2G×3L,所以杠杆左端下沉。
为使杠杆保持水平平衡,根据杠杆平衡条件可得(3G+2G)×2L=2G×nL,解得n=5,所以应将挂在B点的钩码向右移动2格。
(3)用弹簧测力计代替B点悬挂的钩码,并始终竖直向下拉弹簧测力计,使杠杆从水平位置缓慢转过一定角度,则支点左右两侧动力臂和阻力臂均变小,但阻力臂与动力臂的比值不变,由杠杆平衡条件可知,动力与阻力比值不变,在阻力不变时,则动力不变,即弹簧测力计的示数不变。
(4)题图丁中,杠杆的重心不在支点上,杠杆的重力对杠杆转动产生了影响,导致拉力F的大小比由杠杆平衡条件计算出来的数值偏大。
(5)倾斜拉时动力臂减小,阻力和阻力臂不变的情况下,拉力变大。
(6)将弹簧测力计的作用点由点A移至点B,支点O、钩码位置不变,仍将钩码提升相同的高度,这时有用功和总功都不变,根据η=可知,机械效率不变。
实验二 测量滑轮组的机械效率
实验器材 铁架台、定滑轮、动滑轮、钩码、细绳、弹簧测力计、刻度尺。
实验步骤 (1)用弹簧测力计测量钩码的重力G,组装好滑轮组,分别记下钩码和绳端的位置;
(2)缓慢匀速向上拉弹簧测力计,使钩码升高,读出弹簧测力计示数F,用刻度尺测量钩码上升的高度h和绳端移动的距离s;
(3)将实验数据记录在表格中,计算出有用功W有、总功W总、机械效率η;
(4)改变钩码的数量,重复以上实验。
例9 在“测量滑轮组的机械效率”的实验中,小兵与同学们用同一滑轮组进行了三次实验(如图所示)。
实验数据记录如表:
次数 钩码重/N 钩码上升距离/cm 弹簧测力计示数/N 弹簧测力计上升距离/cm 机械效率
1 2 10 0.8 30 83.3%
2 4 10 1.5 30 ①
3 6 10 ② 30 90.9%
[实验设计与进行]
(1)实验时应沿竖直方向________拉动弹簧测力计,并用刻度尺测出钩码上升的高度。
(2)表格中编号①处的数据为________;编号②处的数据为________(观察丙图)。
(3)分析数据可得结论:使用同一滑轮组提升不同重物至同一高度时,提升的物重增加时,所做的额外功________(选填“变大”“变小”或“不变”)。
[分析与论证]
(4)若将此滑轮组换一种绕绳方法,不计绳重和摩擦,提升相同的物体时,滑轮组的机械效率________(选填“改变”或“不变”)。
(5)第二组同学也利用2 N、4 N、6 N的钩码进行三次实验,每次测得的机械效率均大于第一组同学的测量值,不可能的原因是________。
A.测拉力时,弹簧测力计未调零,指针指在零刻度线上方
B.弹簧测力计每次拉动钩码时均加速上升
C.第二组所使用的动滑轮的重力小于第一组
[拓展设问]
(6)小明进一步研究,测出动滑轮的质量为50 g,根据表格中的数据得出:总功总是大于有用功与克服动滑轮重力的功之和,即W总>W有+W轮,他猜测还有________________________因素影响机械效率。(答一种因素即可)
(7)实验表明:额外功越小,总功越接近有用功。进一步推理得出:假设没有额外功,总功等于有用功;可见使用任何机械都不省功。下列物理规律的得出运用了这种研究方法的是________。
A.平面镜成像的规律
B.牛顿第一定律
C.阿基米德原理
[思维提升]
(8)某次实验时将绳子自由端匀速拉动时弹簧测力计的读数记为F,钩码重记为G,动滑轮重记为G′,绳自由端移动距离记为s,钩码提升高度记为h,不计绳重及摩擦。则下列关于滑轮组机械效率的计算公式中正确的是________。
A. B. C.1- D.
[联系实际]
(9)机械效率是衡量机械性能好坏的重要标志,请根据你的生活经验提出一种提高机械效率的措施________________。
答案 (1)匀速 (2)88.9% 2.2 (3)变大 (4)不变 (5)B (6)绳与滑轮之间的摩擦 (7)B (8)B (9)减轻动滑轮的自重
解析 (1)实验时沿竖直方向匀速缓慢拉动弹簧测力计。
(2)第2次实验的机械效率为η====88.9%,
弹簧测力计分度值为0.2 N,示数为2.2 N,故编号②处数据为2.2。
(3)进一步分析数据,可知用同一滑轮组提升不同重物至同一高度,提升的物重增加时,所做的额外功将变大,原因:物重增加,轮和轴之间的压力变大,摩擦力变大。
(4)不计绳重及摩擦,则克服动滑轮的自重做的功为额外功的唯一来源,若将此滑轮组换一种绕绳方法,提升相同的物体时,滑轮组的机械效率:η===,
因G和G动不变,故滑轮组的机械效率不变。
(5)测拉力时,弹簧测力计未调零,指针指在零刻度线上方,拉力测量值偏小,机械效率变大,故A不符合题意;弹簧测力计每次拉动钩码时均加速上升,拉力变大,机械效率变小,故B符合题意;第二组所使用的动滑轮的重力小于第一组,则克服动滑轮重力做的功减小,额外功减小,机械效率变大,故C不符合题意。
(6)实验中,额外功为克服动滑轮重力做的功与克服绳重、各种摩擦做的功之和,即绳重、各种摩擦也会影响机械效率。
(7)实验表明:额外功越小,总功越接近有用功。进一步推理得出:假设没有额外功,总功等于有用功;可见使用任何机械不省功(采用了理想化推理法)。平面镜成像的规律、阿基米德原理可通过实验直接验证;而牛顿第一定律不能用实验直接验证,是在实验的基础上推理得出的,故选B。
(8)不计绳重及摩擦,
有用功为W有=Gh,总功为W总=Fs,所以η==,故A错误;有用功为W有=Gh,总功为W总=(G+G′)h,所以η===,故B正确;额外功W额=G′h,总功为W总=Fs,有用功W有=W总-W额=Fs-G′h,所以η===1-,故C错误;有用功为W有=Gh,总功为W总=Fs,s=nh,所以η====,故D错误。
(9)减轻动滑轮的自重,可减少做的额外功,在有用功一定时,总功减小,滑轮组的机械效率将变大。
考点一 杠杆
1.(教材素材)如图所示为探究杠杆平衡条件的实验装置,实验前已调节杠杆在水平位置平衡,在图示位置挂上钩码,杠杆仍平衡在水平位置,在两边钩码下面分别再加上一个钩码后,下列判断正确的是( )
A.左端下沉 B.右端下沉 C.仍能平衡 D.不能确定
答案 A
解析 两边同时加上一个钩码后,要重新计算两边的力与力臂的乘积,通过计算知F1l1>F2l2,左边下沉,故选A。
2.(2023·湛江雷州市一模)室内垃圾桶平时桶盖关闭不使垃圾散发异味,使用时用脚踩踏板,桶盖开启,根据室内垃圾桶的结构示意图,可确定桶中有两个杠杆在起作用,两杠杆支点为O1、O2。则对应的杠杆分别是( )
A.省力杠杆 省力杠杆 B.省力杠杆 费力杠杆
C.费力杠杆 费力杠杆 D.费力杠杆 省力杠杆
答案 B
解析 用脚踩踏板时,O1点是支点,动力作用在A点,阻力作用在B点。脚踩下踏板时,动力臂大于阻力臂,属于省力杠杆;桶盖开启时,支点是O2,动力作用在C点,阻力作用在桶盖的重心。在打开盖子的过程中,动力臂小于阻力臂,属于费力杠杆,故选B。
3.(2023·天津)如图甲是我国古代汲水装置——桔槔,图乙是它水平静止时的简化模型,该装置是________(填简单机械名称);此时配重物重力为G1,水桶重力为G2,l1∶l2=2∶1,若不计杆重,则G1∶G2=__________。
答案 杠杆 1∶2
解析 根据杠杆原理,由题图甲知,该装置是杠杆;由杠杆平衡条件可得G1×l1=G2×l2,解得==。
考点二 滑轮、滑轮组
4.(2022·广东)分别使用图中四种装置匀速提升同一重物,不计滑轮重、绳重和摩擦,最省力的是( )
答案 A
解析 由题知,不计摩擦和滑轮、绳重,先分析所用的是定滑轮、动滑轮还是滑轮组,若是定滑轮,不省力,F=G;若是动滑轮,省一半力,F=G;若是滑轮组,找出拉动动滑轮绳子股数n,则F=G,故选A。
5.(2021·深圳)如图,两个滑轮组,提升一个重为17 N的物体A(每个滑轮重相同),使物体A在2 s内拉升了20 cm,拉力如图所示,下列说法正确的是(不计绳重与摩擦)( )
A.甲中,绳端移动的距离为60 cm
B.乙中,拉力的功率为1.7 W
C.甲中,动滑轮由两根绳子吊着
D.乙中,动滑轮的重力为2 N
答案 A
解析 由题意可知,不计绳重和摩擦。由题图甲可知,n1=3,则绳自由端移动的距离s1=n1h=3×20 cm=60 cm,故A正确,C错误;由题图乙可知,n2=2,绳自由端移动的速度:v2====0.2 m/s,由P===Fv可知,拉力的功率为P2=F2v2=9×0.2 m/s=1.8 W,故B错误;题图乙中,由F=(GA+G动)可知,动滑轮的重力:G动=2F2-GA=2×9 N-17 N=1 N,故D错误。
考点三 机械效率
6.(2023·成都)如图甲所示装置,小欢用力F向下拉绳子,使物体M在水平地面匀速移动,地面ab、bc粗糙程度不同。物体M重为400 N,动滑轮重为5 N,ab=2 m,bc=3 m。物体M从a点到c点过程中,拉力F与M移动距离的关系如图乙,不考虑物体大小对运动的影响,忽略绳子重力及滑轮转轴摩擦,对此过程的分析,下列结论正确的是( )
A.绳子自由端移动的距离为15 m
B.拉力F做的功为840 J
C.拉力F在ab段做的额外功等于在bc段做的额外功
D.物体从ab段到bc段,滑轮组的机械效率变小
答案 B
解析 物体M从a点到c点过程中,通过的距离为2 m+3 m=5 m,绳子的有效段数为2,故绳子自由端移动的距离sM=2h=2×5 m=10 m,故A错误;ab=2 m,bc=3 m,绳子自由端移动的距离分别为s1=2×2 m=4 m,s2=2×3 m=6 m,由题图乙知绳子的拉力分别为60 N和100 N,拉力做的功为W=W1+W2=F1s1+F2s2=60 N×4 m+100 N×6 m=840 J,故B正确;本题中,克服摩擦力做的功为有用功,忽略绳子重力及滑轮转轴摩擦,故克服动滑轮的重力做的功为额外功,在ab段和在bc段动滑轮提升的高度不同,根据W=Gh,故拉力F在ab段做的额外功不等于在bc段做的额外功,故C错误;使物体M在水平地面匀速移动,根据二力平衡,物体受到的滑动摩擦力等于水平面上绳子的拉力的大小,因100 N大于60 N,故可知bc段物体受到的滑动摩擦力大,滑轮组的机械效率为η=====,动滑轮的重力不变,物体从ab段到bc段,滑动摩擦力变大,故滑轮组的机械效率变大,故D错误。
7.(2021·广东改编)用如图甲所示的滑轮组提升重200 N的物体,已知拉力F为80 N,不计绳重和摩擦,物体和绳子自由端的运动情况如图乙所示,反映绳子自由端运动的图线是________(选填“A”或“B”),3 s内对物体做的有用功为________ J,机械效率为________。
答案 A 300 83.3%
解析 由题图甲可知,n=3,则绳子自由端移动距离s=3h,据此确定题图乙中绳子自由端运动的图线是A。由题图乙可知,t=3 s时,物体运动的高度h=1.5 m,有用功W=Gh=200 N×1.5 m=300 J。总功是W=Fs,机械效率η====83.3%。
8.(2023·广州改编)如图物体A以2 cm/s的速度,在水平地面上做匀速直线运动,此时弹簧测力计的示数为3 N,绳子自由端水平拉力F=________ N,物体受到的摩擦力f=5 N,2 s内绳子自由端移动的距离为________ m,滑轮组的机械效率是________。(不计轮与绳之间的摩擦)
答案 3 0.08 83.3%
解析 因为拉力F与弹簧测力计的示数相等,所以F=3 N。因为动滑轮省一半力,但要多移动一倍的距离,所以绳子自由端运动的速度是物体A运动速度的2倍。所以,v绳=2vA=2×2 cm/s=4 cm/s,s=2 s×4 cm/s=8 cm=0.08 m。滑轮组的机械效率η======83.3%。
9.(2023·深圳)如图甲是古代劳动人民用工具撬起木料的情景,如图乙中已知其中BO∶OC=1∶5,木料的体积为4 m3,木料的密度为0.5×103 kg/m3(g取10 N/kg)。
(1)求木料所受重力;
(2)如图乙,在B端有一木料对绳子的力F1为1×104 N,当F2为多大时,木料刚好被抬起?
(3)随着时代发展,亮亮同学发现吊车能更方便地提起重物。如图丙用一吊车匀速向上提起木料,已知提升的功率为P=10 kW,那这个吊车在10 s内可以将该木料提升的高度为多高?
解:(1)木料的体积为4 m3,木料的密度为0.5×103 kg/m3,则木料所受重力G=mg=ρVg=0.5×103 kg/m3×4 m3×10 N/kg=2×104 N。
(2)在B端有一木料对绳子的力F1为1×104 N,由杠杆平衡条件可得F1·OB=F2·OC
由于BO∶OC=1∶5,
则木料刚好被抬起时,力F2===2×103 N。
(3)提升的功率为P=10 kW,由P===Fv得吊车匀速向上提起木料,拉力等于木料重力,则提升速度v====0.5 m/s,
吊车在10 s内可以将该木料提升的高度h=vt=0.5 m/s×10 s=5 m。
答:(1)木料所受重力为2×104 N;
(2)当F2为2×103 N时,木料刚好被抬起;
(3)吊车在10 s内可以将该木料提升的高度为5 m。
10.(从生活到物理)小蒲同学是一个爱思考问题的同学,他看到某小区正在建造的楼房地基上有起重机在不停地吊起地面上的建筑材料,于是他查阅了起重机资料,下面是其中某一款塔式起重机简易示意图(如图甲),小蒲知道了塔式起重机主要用于房屋建筑中材料的输送及建筑构件的安装(动滑轮重、绳重及摩擦不计,g取10 N/kg)。
(1)为保持平衡,起重臂的长度越长的塔式起重机,配备的平衡重的质量应越______(选填“大”或“小”)。
(2)图乙为起重机钢丝绳穿绳简化示意图,滑轮a是________(选填“动滑轮”或“定滑轮”),若钢丝绳能承受的最大拉力为3×104 N,则能吊起货物的质量不能超过________ kg。
(3)换用如图丙所示滑轮组,在需要考虑动滑轮重力的情形下,用拉力F将重为8 000 N的物体匀速在5 s时间内提升了0.5 m,若滑轮组的机械效率η为80%,则该过程中拉力F所做功的功率为______ W。
答案 (1)大 (2)定滑轮 6×103 (3)1 000
解析 (1)由杠杆的平衡条件可知G配重l左=F右l右,则G配重=F右,
由题意可知,l左、F右不变,l右越长,则G配重越大,由G=mg可知,配备的平衡重的质量应越大。
(2)由题图乙可知,滑轮a固定不动,因此滑轮a为定滑轮,因为动滑轮重、绳重及摩擦不计时F=G,所以能吊起货物的最大重力G=2F=2×3×104 N=6×104 N,
由G=mg可知,能吊起货物的最大质量m物===6×103 kg。
(3)由题图丙可知n′=2,有用功W有=G′h′=8 000 N×0.5 m=4 000 J,
由η=可知,拉力做的总功W总===5 000 J,
拉力所做功的功率P===1 000 W。
11.(2023·珠海香洲区二模)我国劳动人民很早就在农业、军事等方面应用杠杆,如图所示。
(1)以上四种应用中属于费力杠杆的是________(多选,选填字母)。
(2)利用图A中的脚踏碓捣谷时,劳作者踩踏碓尾,碓头高高抬起,松脚后碓头下落过程中,它的重力势能会________(选填“变大”“不变”或“变小”)。为了省力些,可将脚踩点适当________(选填“远离”或“靠近”)O点。
(3)脚踏碓的脚踩位置有粗糙的花纹,这是为了________(选填“增大”或“减小”)摩擦。
(4)如图C所示是护城河上安装的吊桥。在拉起吊桥过程中,滑轮的作用是________________。从图甲缓缓拉起到图乙的过程中,人用的力将________(选填“变大”“不变”或“变小”),若桥身木板总质量为60 kg,长5 m,不计绳重及摩擦,桥身在乙图位置时,拉力F的大小是________ N。(g取10 N/kg)
答案 (1)AB (2)变小 远离 (3)增大 (4)改变力的方向 变小 240
解析 (1)根据杠杆的分类,动力臂比阻力臂短的杠杆是费力杠杆,A、B是费力杠杆,C、D是省力杠杆。
(2)松脚后碓头下落过程中,质量不变,高度减小,它的重力势能会变小。为了省力些,根据杠杆原理,在阻力和阻力臂一定时,动力臂越大,越省力,可将脚踩点适当远离O点。
(3)在压力一定时,接触面的粗糙程度越大,滑动摩擦力越大。脚踏碓的脚踩位置有粗糙的花纹,这是为了增大摩擦。
(4)题图C中的滑轮是一个定滑轮,定滑轮不省力,可以改变力的方向。从图甲缓缓拉起到图乙的过程中,根据杠杆的平衡条件,F1=可知:阻力一定,阻力臂减小,动力臂增大,人用的力将变小。
木板的重力为:G=mg=60 kg×10 N/kg=600 N;
根据杠杆的平衡条件有:F×5 m=G×2 m;
所以F===240 N。
命题分析
广东省近五年中考物理命题分析
考点 2023 2022 2021 2020 2019
杠杆 省题16、21 省题17 省题20 省题15 省题15
滑轮 ___ 省题6 省题14 省题14 省题19
机械效率 ___ ___ ___ ___ ___
【课程标准】
2.2.6 知道简单机械。探究并了解杠杆的平衡条件。
3.2.3 知道机械效率。了解提高机械效率的意义和途径。
例 测量某种简单机械的机械效率。
3.2.4 能说出人类使用的一些机械。了解机械的使用对社会发展的作用。
4.2.5 探究杠杆的平衡条件。
例 用杠杆、铁架台、钩码和弹簧测力计,探究杠杆平衡时动力、动力臂与阻力、阻力臂之间的定量关系。
考点一 杠杆
一、认识杠杆
1.定义:一根硬棒,在力的作用下能绕着固定点O转动,这根硬棒就是杠杆。
2.关于杠杆的名词
(1)支点:杠杆可以绕其转动的点O。
(2)动力:使杠杆转动的力F1。
(3)阻力:阻碍杠杆转动的力F2。
(4)动力臂:从支点到动力F1作用线的距离l1。
(5)阻力臂:从支点到阻力F2作用线的距离l2。
3.杠杆的平衡条件:动力×动力臂=阻力×阻力臂,或写为F1l1=F2l2。
注意:计算时,动力F1和阻力F2单位要统一,动力臂l1和阻力臂l2单位也要统一。
二、杠杆应用
种类 省力杠杆 费力杠杆 等臂杠杆
图例
力臂关系 l1>l2 l1<l2 l1=l2
力的关系 F1<F2 F1>F2 F1=F2
特点 省力费距离 省距离费力 既不省力也不费距离
实例 钢丝钳 钓鱼竿 天平
(1)杠杆一定是直的。( × )
(2)支点一定在杠杆上。( √ )
(3)力臂是杠杆的支点到力的作用点的距离。( × )
(4)同一个杠杆,动力臂和阻力臂的长度是不变的,与动力和阻力的方向无关。( × )
(5)只要设计合理,同一杠杆既可以省力也可以省距离。( × )
(6)能够省力的杠杆,一定费距离。( √ )
例1 (2020·广东)如图所示,用一根硬棒通过支点O撬起石头,画出石头所受重力G的示意图,以及力F的力臂l。
答案
解析 石头重力的作用点在重心,过重心沿竖直向下的方向画一条带箭头的线段,并用符号G表示;过支点O作垂直于动力作用线的垂线段,即为F的力臂l。
例2 (2023·广州越秀区模拟)如图,重力为G、质量分布均匀的木棒左端与支点O连接,绕O转动时,棒所受的摩擦力可忽略不计。棒重心处受到竖直向上的拉力F1保持静止,则( )
A.F1=G
B.F1·OA=G·OB
C.若F1为杠杆的动力,G为杠杆的阻力,此杠杆为费力杠杆
D.若将竖直拉力移到C点棒仍静止,此时拉力记为F2,则F1<F2
答案 A
解析 由题图可知,竖直向上的拉力F1作用在棒重心处,力臂为OB,因为木棒质量分布均匀,则杠杆自身重力的力臂也为OB,若F1为杠杆的动力,G为杠杆的阻力,根据杠杆平衡条件可知,F1·OB=G·OB,由F1=G,此时动力和阻力大小相同,是一个等臂杠杆,故A正确,B、C错误;若将竖直拉力移到C点,棒仍静止且大小为F2,此时F2的力臂相比F1的力臂变长,杠杆自身重力不变,重力的力臂不变,根据杠杆平衡条件可知,拉力F2变小,则F1>F2,故D错误。
名师点拨 (1)凡省力的杠杆必定费距离,凡省距离的杠杆必定费力。 (2)判断杠杆的种类,主要通过动力臂和阻力臂的大小进行判断,对于一些不容易判断力臂大小的杠杆,可根据使用杠杆的目的(是省距离还是省力)来判断,如用筷子吃饭时省距离,则筷子为费力杠杆。
例3 (2023·广州)图甲中工人用工具搬运石头,该工具可简化成图乙中杠杆AB,移动支架,可使支点O在AB间移动。杆水平静止,忽略杆重。
(1)人对杆的压力为F1,绳对杆的拉力为F2,F1、F2竖直向下。
①在图乙中画出F1的力臂l1;
②F2的力臂l2=________(用F1、F2、l1表示)。
(2)同一石头仍悬挂在杆B端,人对杆A端的压力方向不变,只通过移动支点O使该压力变小,杆仍保持水平静止,支点O应向________(选填“A”或“B”)端移动。
答案 (1)①如图所示 ② (2)B
解析 (1)①题图乙中支点是O,过支点作力F1作用线的垂线,标上垂足,标出这段距离,记为l1,如答图所示。
②根据杠杆的平衡条件得F1l1=F2l2,F2的力臂l2=。
(2)同一石头仍悬挂在杆B端,人对杆A端的压力方向不变,只通过移动支点O使该压力变小,杆仍保持水平静止,支点O应向B端移动,使得阻力臂减小,同时动力臂变大。
考点二 滑轮、滑轮组
滑轮、滑轮组
方向 竖直提升物体 水平拉动物体
滑轮 定滑轮 动滑轮 滑轮组
图例
特点 可以改变力的方向 可以省力 既可以省力又可以改变力的方向
拉力情况(不计绳重和摩擦) F1=G F2=(G+G动) F3=(G+G动) F4=f
绳子自由端移动的距离s s=h s=2h s=nh s=ns物
(1)使用定滑轮一定不省力。( √ )
(2)使用动滑轮一定能省一半的力。( × )
(3)使用滑轮组既可以省力又可以省距离。( × )
(4)使用滑轮组既可以省力又可以改变用力的方向。( √ )
(5)定滑轮和动滑轮都可以看成一个变形的杠杆。( √ )
例4 (2023·重庆)在美丽乡村建设的工地上,如图所示,工人借助动滑轮用250 N的拉力,将450 N的重物匀速提升2 m,用时10 s。则( )
A.重物上升的速度为0.4 m/s B.动滑轮做的有用功为1 000 J
C.工人的拉力的功率为90 W D.拉力做的总功1 000 J
答案 D
解析 重物上升的速度v===0.2 m/s,故A错误;动滑轮做的有用功W有=Gh=450 N×2 m=900 J,故B错误;由题图可知,绳子自由端移动的距离s=nh=2×2 m=4 m,拉力做的总功W总=Fs=250 N×4 m=1 000 J,拉力做功的功率P===100 W,故C错误,D正确。
例5 (2023·肇庆怀集县一模)如图所示,小明同学想把被台风刮倒的甲树拉正,他把绳子的一端系在乙树上,然后绕过甲树用力拉绳子,这样做时甲树干相当于________(选填“动滑轮”“定滑轮”或“杠杆”)。如果不计绳重和摩擦,甲树受到500 N拉力,则小明对绳子的拉力为________ N,乙树受到的拉力为________ N。
答案 动滑轮 250 250
解析 把绳子的一端系在乙树上,然后绕过甲树用力拉绳子时,甲树干要移动,则甲树干相当于动滑轮;拉甲树干的绳子段数是2,不计绳重和摩擦,所以小明对绳子的拉力F=×500 N=250 N,乙树受到的拉力等于1段绳子的拉力,大小为250 N。
考点三 机械效率
1.机械效率定义:有用功跟总功的比值。
用公式表示η=。
2.使用机械时,有用功总是小于总功,机械效率总是小于1,机械效率通常用百分数表示。
3.常见简单机械的机械效率
简单机械 定滑轮 动滑轮、滑轮组 斜面
图例
有用功 W有=Gh W有=Gh W有=Gh
总功 W总=Fs W总=Fs W总=Fs
机械效率 η= η=== η==
(1)同一个滑轮组,其机械效率是固定不变的。( × )
(2)功率大的机械,机械效率一定高。( × )
(3)越省力的机械,机械效率越高。( × )
(4)所做有用功越多的机械,机械效率越高。( × )
(5)做功相等的情况下,额外功越少的机械,机械效率越高。( √ )
例6 (2023·佛山禅城区一模)如图所示,用两个完全相同的滑轮匀速提升所受重力相等的物体。不计轴处摩擦,比较甲、乙装置可知( )
A.甲省力,机械效率较高
B.甲不省力,机械效率较低
C.乙省力,机械效率较低
D.乙不省力,机械效率较高
答案 D
解析 定滑轮不省力,不用对滑轮做功,故机械效率高;动滑轮省力,但要对滑轮做额外功,故机械效率低,故选D。
例7 (2023·惠州一模)如图所示,把重为200 N的物体匀速提升2 m,不计滑轮、绳子的重力及摩擦,所用拉力F为________ N,拉力所做的功为________ J;若拉力为110 N,滑轮组的机械效率为________。
答案 100 400 90.9%
解析 由滑轮组可知,承重绳子的有效股数n=2,
拉力F===100 N;
绳子自由端移动的距离s=nh=2×2 m=4 m,
拉力做的功W=Fs=100 N×4 m=400 J;
若拉力为110 N,
由滑轮组的机械效率公式可知滑轮组的机械效率η===90.9%。
实验一 探究杠杆的平衡条件
实验器材 铁架台、杠杆、钩码、细绳。
实验步骤 (1)将杠杆固定在铁架台上,调节杠杆两端的平衡螺母,使杠杆在水平位置保持平衡;
(2)给杠杆两侧挂钩码,移动钩码的位置,使杠杆重新在水平位置平衡,读出平衡时动力、动力臂、阻力、阻力臂的数值填入表格中;
(3)改变动力、动力臂的大小,相应调节阻力、阻力臂,再重复做几次实验。
实验结论 动力×动力臂=阻力×阻力臂(或F1l1=F2l2)。
例8 小明在“探究杠杆平衡条件”的实验中,采用了如图甲所示的实验装置(实验中所用钩码均相同,杠杆质量均匀,相邻刻度线之间的距离相等)。
[实验设计与进行]
(1)实验前杠杆左端高、右端低,此时杠杆处于________(选填“平衡”或“非平衡”)状态。接下来应将杠杆左端的平衡螺母向________(选填“左”或“右”,下同)调节,或将杠杆右端的平衡螺母向______调节,使杠杆处于水平静止状态。
(2)图乙中杠杆恰好处于水平位置平衡,小明尝试在A点下方再加挂2个相同的钩码,则杠杆______(选填“左”或“右”)端会下沉,为使杠杆保持水平平衡,他可以将挂在B点的钩码________________(填具体操作)。
(3)小明又尝试用弹簧测力计代替B点悬挂的钩码,并始终竖直向下拉弹簧测力计,使杠杆从水平位置缓慢转过一定角度,如图丙所示。此过程中弹簧测力计的示数会________(选填“变大”“变小”或“不变”)。(不计阻力影响)
[拓展设问]
(4)小刚同学用图丁所示的装置进行探究,发现当杠杆水平平衡时,与小明同学得出的杠杆平衡条件不相符,其可能的原因是____________________________________________。
(5)小刚同学如果改为倾斜拉弹簧测力计,杠杆还是平衡,弹簧测力计的示数________(选填“变大”“变小”或“不变”)。
(6)小刚用丁图的装置测杠杆的机械效率,若把弹簧测力计由A点移到B点,仍将钩码提升相同的高度,则杠杆的机械效率将________(选填“变大”“变小”或“不变”)。
答案 (1)平衡 左 左 (2)左 向右移动2格 (3)不变 (4)杠杆的重力对杠杆转动产生了影响 (5)变大 (6)不变
解析 (1)杠杆静止时处于平衡状态;杠杆右端下沉,为了使杠杆在水平位置平衡,则他应将杠杆左端的平衡螺母向左调节,或将杠杆右端的平衡螺母向左调节。
(2)设杠杆的一个小格为L,一个钩码重为G,小明尝试在A点下方再加挂2个相同的钩码,(3G+2G)×2L>2G×3L,所以杠杆左端下沉。
为使杠杆保持水平平衡,根据杠杆平衡条件可得(3G+2G)×2L=2G×nL,解得n=5,所以应将挂在B点的钩码向右移动2格。
(3)用弹簧测力计代替B点悬挂的钩码,并始终竖直向下拉弹簧测力计,使杠杆从水平位置缓慢转过一定角度,则支点左右两侧动力臂和阻力臂均变小,但阻力臂与动力臂的比值不变,由杠杆平衡条件可知,动力与阻力比值不变,在阻力不变时,则动力不变,即弹簧测力计的示数不变。
(4)题图丁中,杠杆的重心不在支点上,杠杆的重力对杠杆转动产生了影响,导致拉力F的大小比由杠杆平衡条件计算出来的数值偏大。
(5)倾斜拉时动力臂减小,阻力和阻力臂不变的情况下,拉力变大。
(6)将弹簧测力计的作用点由点A移至点B,支点O、钩码位置不变,仍将钩码提升相同的高度,这时有用功和总功都不变,根据η=可知,机械效率不变。
实验二 测量滑轮组的机械效率
实验器材 铁架台、定滑轮、动滑轮、钩码、细绳、弹簧测力计、刻度尺。
实验步骤 (1)用弹簧测力计测量钩码的重力G,组装好滑轮组,分别记下钩码和绳端的位置;
(2)缓慢匀速向上拉弹簧测力计,使钩码升高,读出弹簧测力计示数F,用刻度尺测量钩码上升的高度h和绳端移动的距离s;
(3)将实验数据记录在表格中,计算出有用功W有、总功W总、机械效率η;
(4)改变钩码的数量,重复以上实验。
例9 在“测量滑轮组的机械效率”的实验中,小兵与同学们用同一滑轮组进行了三次实验(如图所示)。
实验数据记录如表:
次数 钩码重/N 钩码上升距离/cm 弹簧测力计示数/N 弹簧测力计上升距离/cm 机械效率
1 2 10 0.8 30 83.3%
2 4 10 1.5 30 ①
3 6 10 ② 30 90.9%
[实验设计与进行]
(1)实验时应沿竖直方向________拉动弹簧测力计,并用刻度尺测出钩码上升的高度。
(2)表格中编号①处的数据为________;编号②处的数据为________(观察丙图)。
(3)分析数据可得结论:使用同一滑轮组提升不同重物至同一高度时,提升的物重增加时,所做的额外功________(选填“变大”“变小”或“不变”)。
[分析与论证]
(4)若将此滑轮组换一种绕绳方法,不计绳重和摩擦,提升相同的物体时,滑轮组的机械效率________(选填“改变”或“不变”)。
(5)第二组同学也利用2 N、4 N、6 N的钩码进行三次实验,每次测得的机械效率均大于第一组同学的测量值,不可能的原因是________。
A.测拉力时,弹簧测力计未调零,指针指在零刻度线上方
B.弹簧测力计每次拉动钩码时均加速上升
C.第二组所使用的动滑轮的重力小于第一组
[拓展设问]
(6)小明进一步研究,测出动滑轮的质量为50 g,根据表格中的数据得出:总功总是大于有用功与克服动滑轮重力的功之和,即W总>W有+W轮,他猜测还有________________________因素影响机械效率。(答一种因素即可)
(7)实验表明:额外功越小,总功越接近有用功。进一步推理得出:假设没有额外功,总功等于有用功;可见使用任何机械都不省功。下列物理规律的得出运用了这种研究方法的是________。
A.平面镜成像的规律
B.牛顿第一定律
C.阿基米德原理
[思维提升]
(8)某次实验时将绳子自由端匀速拉动时弹簧测力计的读数记为F,钩码重记为G,动滑轮重记为G′,绳自由端移动距离记为s,钩码提升高度记为h,不计绳重及摩擦。则下列关于滑轮组机械效率的计算公式中正确的是________。
A. B. C.1- D.
[联系实际]
(9)机械效率是衡量机械性能好坏的重要标志,请根据你的生活经验提出一种提高机械效率的措施________________。
答案 (1)匀速 (2)88.9% 2.2 (3)变大 (4)不变 (5)B (6)绳与滑轮之间的摩擦 (7)B (8)B (9)减轻动滑轮的自重
解析 (1)实验时沿竖直方向匀速缓慢拉动弹簧测力计。
(2)第2次实验的机械效率为η====88.9%,
弹簧测力计分度值为0.2 N,示数为2.2 N,故编号②处数据为2.2。
(3)进一步分析数据,可知用同一滑轮组提升不同重物至同一高度,提升的物重增加时,所做的额外功将变大,原因:物重增加,轮和轴之间的压力变大,摩擦力变大。
(4)不计绳重及摩擦,则克服动滑轮的自重做的功为额外功的唯一来源,若将此滑轮组换一种绕绳方法,提升相同的物体时,滑轮组的机械效率:η===,
因G和G动不变,故滑轮组的机械效率不变。
(5)测拉力时,弹簧测力计未调零,指针指在零刻度线上方,拉力测量值偏小,机械效率变大,故A不符合题意;弹簧测力计每次拉动钩码时均加速上升,拉力变大,机械效率变小,故B符合题意;第二组所使用的动滑轮的重力小于第一组,则克服动滑轮重力做的功减小,额外功减小,机械效率变大,故C不符合题意。
(6)实验中,额外功为克服动滑轮重力做的功与克服绳重、各种摩擦做的功之和,即绳重、各种摩擦也会影响机械效率。
(7)实验表明:额外功越小,总功越接近有用功。进一步推理得出:假设没有额外功,总功等于有用功;可见使用任何机械不省功(采用了理想化推理法)。平面镜成像的规律、阿基米德原理可通过实验直接验证;而牛顿第一定律不能用实验直接验证,是在实验的基础上推理得出的,故选B。
(8)不计绳重及摩擦,
有用功为W有=Gh,总功为W总=Fs,所以η==,故A错误;有用功为W有=Gh,总功为W总=(G+G′)h,所以η===,故B正确;额外功W额=G′h,总功为W总=Fs,有用功W有=W总-W额=Fs-G′h,所以η===1-,故C错误;有用功为W有=Gh,总功为W总=Fs,s=nh,所以η====,故D错误。
(9)减轻动滑轮的自重,可减少做的额外功,在有用功一定时,总功减小,滑轮组的机械效率将变大。
考点一 杠杆
1.(教材素材)如图所示为探究杠杆平衡条件的实验装置,实验前已调节杠杆在水平位置平衡,在图示位置挂上钩码,杠杆仍平衡在水平位置,在两边钩码下面分别再加上一个钩码后,下列判断正确的是( )
A.左端下沉 B.右端下沉 C.仍能平衡 D.不能确定
答案 A
解析 两边同时加上一个钩码后,要重新计算两边的力与力臂的乘积,通过计算知F1l1>F2l2,左边下沉,故选A。
2.(2023·湛江雷州市一模)室内垃圾桶平时桶盖关闭不使垃圾散发异味,使用时用脚踩踏板,桶盖开启,根据室内垃圾桶的结构示意图,可确定桶中有两个杠杆在起作用,两杠杆支点为O1、O2。则对应的杠杆分别是( )
A.省力杠杆 省力杠杆 B.省力杠杆 费力杠杆
C.费力杠杆 费力杠杆 D.费力杠杆 省力杠杆
答案 B
解析 用脚踩踏板时,O1点是支点,动力作用在A点,阻力作用在B点。脚踩下踏板时,动力臂大于阻力臂,属于省力杠杆;桶盖开启时,支点是O2,动力作用在C点,阻力作用在桶盖的重心。在打开盖子的过程中,动力臂小于阻力臂,属于费力杠杆,故选B。
3.(2023·天津)如图甲是我国古代汲水装置——桔槔,图乙是它水平静止时的简化模型,该装置是________(填简单机械名称);此时配重物重力为G1,水桶重力为G2,l1∶l2=2∶1,若不计杆重,则G1∶G2=__________。
答案 杠杆 1∶2
解析 根据杠杆原理,由题图甲知,该装置是杠杆;由杠杆平衡条件可得G1×l1=G2×l2,解得==。
考点二 滑轮、滑轮组
4.(2022·广东)分别使用图中四种装置匀速提升同一重物,不计滑轮重、绳重和摩擦,最省力的是( )
答案 A
解析 由题知,不计摩擦和滑轮、绳重,先分析所用的是定滑轮、动滑轮还是滑轮组,若是定滑轮,不省力,F=G;若是动滑轮,省一半力,F=G;若是滑轮组,找出拉动动滑轮绳子股数n,则F=G,故选A。
5.(2021·深圳)如图,两个滑轮组,提升一个重为17 N的物体A(每个滑轮重相同),使物体A在2 s内拉升了20 cm,拉力如图所示,下列说法正确的是(不计绳重与摩擦)( )
A.甲中,绳端移动的距离为60 cm
B.乙中,拉力的功率为1.7 W
C.甲中,动滑轮由两根绳子吊着
D.乙中,动滑轮的重力为2 N
答案 A
解析 由题意可知,不计绳重和摩擦。由题图甲可知,n1=3,则绳自由端移动的距离s1=n1h=3×20 cm=60 cm,故A正确,C错误;由题图乙可知,n2=2,绳自由端移动的速度:v2====0.2 m/s,由P===Fv可知,拉力的功率为P2=F2v2=9×0.2 m/s=1.8 W,故B错误;题图乙中,由F=(GA+G动)可知,动滑轮的重力:G动=2F2-GA=2×9 N-17 N=1 N,故D错误。
考点三 机械效率
6.(2023·成都)如图甲所示装置,小欢用力F向下拉绳子,使物体M在水平地面匀速移动,地面ab、bc粗糙程度不同。物体M重为400 N,动滑轮重为5 N,ab=2 m,bc=3 m。物体M从a点到c点过程中,拉力F与M移动距离的关系如图乙,不考虑物体大小对运动的影响,忽略绳子重力及滑轮转轴摩擦,对此过程的分析,下列结论正确的是( )
A.绳子自由端移动的距离为15 m
B.拉力F做的功为840 J
C.拉力F在ab段做的额外功等于在bc段做的额外功
D.物体从ab段到bc段,滑轮组的机械效率变小
答案 B
解析 物体M从a点到c点过程中,通过的距离为2 m+3 m=5 m,绳子的有效段数为2,故绳子自由端移动的距离sM=2h=2×5 m=10 m,故A错误;ab=2 m,bc=3 m,绳子自由端移动的距离分别为s1=2×2 m=4 m,s2=2×3 m=6 m,由题图乙知绳子的拉力分别为60 N和100 N,拉力做的功为W=W1+W2=F1s1+F2s2=60 N×4 m+100 N×6 m=840 J,故B正确;本题中,克服摩擦力做的功为有用功,忽略绳子重力及滑轮转轴摩擦,故克服动滑轮的重力做的功为额外功,在ab段和在bc段动滑轮提升的高度不同,根据W=Gh,故拉力F在ab段做的额外功不等于在bc段做的额外功,故C错误;使物体M在水平地面匀速移动,根据二力平衡,物体受到的滑动摩擦力等于水平面上绳子的拉力的大小,因100 N大于60 N,故可知bc段物体受到的滑动摩擦力大,滑轮组的机械效率为η=====,动滑轮的重力不变,物体从ab段到bc段,滑动摩擦力变大,故滑轮组的机械效率变大,故D错误。
7.(2021·广东改编)用如图甲所示的滑轮组提升重200 N的物体,已知拉力F为80 N,不计绳重和摩擦,物体和绳子自由端的运动情况如图乙所示,反映绳子自由端运动的图线是________(选填“A”或“B”),3 s内对物体做的有用功为________ J,机械效率为________。
答案 A 300 83.3%
解析 由题图甲可知,n=3,则绳子自由端移动距离s=3h,据此确定题图乙中绳子自由端运动的图线是A。由题图乙可知,t=3 s时,物体运动的高度h=1.5 m,有用功W=Gh=200 N×1.5 m=300 J。总功是W=Fs,机械效率η====83.3%。
8.(2023·广州改编)如图物体A以2 cm/s的速度,在水平地面上做匀速直线运动,此时弹簧测力计的示数为3 N,绳子自由端水平拉力F=________ N,物体受到的摩擦力f=5 N,2 s内绳子自由端移动的距离为________ m,滑轮组的机械效率是________。(不计轮与绳之间的摩擦)
答案 3 0.08 83.3%
解析 因为拉力F与弹簧测力计的示数相等,所以F=3 N。因为动滑轮省一半力,但要多移动一倍的距离,所以绳子自由端运动的速度是物体A运动速度的2倍。所以,v绳=2vA=2×2 cm/s=4 cm/s,s=2 s×4 cm/s=8 cm=0.08 m。滑轮组的机械效率η======83.3%。
9.(2023·深圳)如图甲是古代劳动人民用工具撬起木料的情景,如图乙中已知其中BO∶OC=1∶5,木料的体积为4 m3,木料的密度为0.5×103 kg/m3(g取10 N/kg)。
(1)求木料所受重力;
(2)如图乙,在B端有一木料对绳子的力F1为1×104 N,当F2为多大时,木料刚好被抬起?
(3)随着时代发展,亮亮同学发现吊车能更方便地提起重物。如图丙用一吊车匀速向上提起木料,已知提升的功率为P=10 kW,那这个吊车在10 s内可以将该木料提升的高度为多高?
解:(1)木料的体积为4 m3,木料的密度为0.5×103 kg/m3,则木料所受重力G=mg=ρVg=0.5×103 kg/m3×4 m3×10 N/kg=2×104 N。
(2)在B端有一木料对绳子的力F1为1×104 N,由杠杆平衡条件可得F1·OB=F2·OC
由于BO∶OC=1∶5,
则木料刚好被抬起时,力F2===2×103 N。
(3)提升的功率为P=10 kW,由P===Fv得吊车匀速向上提起木料,拉力等于木料重力,则提升速度v====0.5 m/s,
吊车在10 s内可以将该木料提升的高度h=vt=0.5 m/s×10 s=5 m。
答:(1)木料所受重力为2×104 N;
(2)当F2为2×103 N时,木料刚好被抬起;
(3)吊车在10 s内可以将该木料提升的高度为5 m。
10.(从生活到物理)小蒲同学是一个爱思考问题的同学,他看到某小区正在建造的楼房地基上有起重机在不停地吊起地面上的建筑材料,于是他查阅了起重机资料,下面是其中某一款塔式起重机简易示意图(如图甲),小蒲知道了塔式起重机主要用于房屋建筑中材料的输送及建筑构件的安装(动滑轮重、绳重及摩擦不计,g取10 N/kg)。
(1)为保持平衡,起重臂的长度越长的塔式起重机,配备的平衡重的质量应越______(选填“大”或“小”)。
(2)图乙为起重机钢丝绳穿绳简化示意图,滑轮a是________(选填“动滑轮”或“定滑轮”),若钢丝绳能承受的最大拉力为3×104 N,则能吊起货物的质量不能超过________ kg。
(3)换用如图丙所示滑轮组,在需要考虑动滑轮重力的情形下,用拉力F将重为8 000 N的物体匀速在5 s时间内提升了0.5 m,若滑轮组的机械效率η为80%,则该过程中拉力F所做功的功率为______ W。
答案 (1)大 (2)定滑轮 6×103 (3)1 000
解析 (1)由杠杆的平衡条件可知G配重l左=F右l右,则G配重=F右,
由题意可知,l左、F右不变,l右越长,则G配重越大,由G=mg可知,配备的平衡重的质量应越大。
(2)由题图乙可知,滑轮a固定不动,因此滑轮a为定滑轮,因为动滑轮重、绳重及摩擦不计时F=G,所以能吊起货物的最大重力G=2F=2×3×104 N=6×104 N,
由G=mg可知,能吊起货物的最大质量m物===6×103 kg。
(3)由题图丙可知n′=2,有用功W有=G′h′=8 000 N×0.5 m=4 000 J,
由η=可知,拉力做的总功W总===5 000 J,
拉力所做功的功率P===1 000 W。
11.(2023·珠海香洲区二模)我国劳动人民很早就在农业、军事等方面应用杠杆,如图所示。
(1)以上四种应用中属于费力杠杆的是________(多选,选填字母)。
(2)利用图A中的脚踏碓捣谷时,劳作者踩踏碓尾,碓头高高抬起,松脚后碓头下落过程中,它的重力势能会________(选填“变大”“不变”或“变小”)。为了省力些,可将脚踩点适当________(选填“远离”或“靠近”)O点。
(3)脚踏碓的脚踩位置有粗糙的花纹,这是为了________(选填“增大”或“减小”)摩擦。
(4)如图C所示是护城河上安装的吊桥。在拉起吊桥过程中,滑轮的作用是________________。从图甲缓缓拉起到图乙的过程中,人用的力将________(选填“变大”“不变”或“变小”),若桥身木板总质量为60 kg,长5 m,不计绳重及摩擦,桥身在乙图位置时,拉力F的大小是________ N。(g取10 N/kg)
答案 (1)AB (2)变小 远离 (3)增大 (4)改变力的方向 变小 240
解析 (1)根据杠杆的分类,动力臂比阻力臂短的杠杆是费力杠杆,A、B是费力杠杆,C、D是省力杠杆。
(2)松脚后碓头下落过程中,质量不变,高度减小,它的重力势能会变小。为了省力些,根据杠杆原理,在阻力和阻力臂一定时,动力臂越大,越省力,可将脚踩点适当远离O点。
(3)在压力一定时,接触面的粗糙程度越大,滑动摩擦力越大。脚踏碓的脚踩位置有粗糙的花纹,这是为了增大摩擦。
(4)题图C中的滑轮是一个定滑轮,定滑轮不省力,可以改变力的方向。从图甲缓缓拉起到图乙的过程中,根据杠杆的平衡条件,F1=可知:阻力一定,阻力臂减小,动力臂增大,人用的力将变小。
木板的重力为:G=mg=60 kg×10 N/kg=600 N;
根据杠杆的平衡条件有:F×5 m=G×2 m;
所以F===240 N。
同课章节目录
