9.2.4 总体离散程度的估计分层练习(含解析)--人教A版(2019)高数必修二
文档属性
| 名称 | 9.2.4 总体离散程度的估计分层练习(含解析)--人教A版(2019)高数必修二 |

|
|
| 格式 | docx | ||
| 文件大小 | 487.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
9.2.4 总体离散程度的估计
基础强化
1.下列说法正确的是( )
A.在两组数据中,平均数较大的一组方差较大
B.平均数反映数据的集中趋势,方差则反映数据离平均数波动的幅度大小
C.方差的求法是求出各个数据与平均数的差的平方后再求和
D.在记录两个人射击环数的两组数据中,方差大的表示射击水平高
2.数据5,7,7,8,10,11的标准差是( )
A.8 B.4
C.2 D.1
3.在高一期中考试中,甲、乙两个班的数学成绩统计如下表:
班级 人数 平均分数 方差
甲 20 甲 2
乙 30 乙 3
其中甲=乙,则两个班数学成绩的方差为( )
A.3 B.2 C.2.6 D.2.5
4.某校为调查高一年级的某次考试的数学成绩情况,随机调查高一年级甲班10名学生,成绩的平均数为90,方差为3,乙班15名学生,成绩的平均数为85,方差为5,则这25名学生成绩的平均数和方差分别为( )
A.87,10.2 B.85,10.2 C.87,10 D.85,10
5.(多选)甲、乙两支女子曲棍球队在去年的国际联赛中,甲队平均每场的进球数是3.2,全年进球数的标准差为3;乙队平均每场的进球数是1.8,全年进球数的标准差为0.3.下列说法中正确的是( )
A.乙队的技术比甲队好
B.乙队发挥比甲队稳定
C.乙队几乎每场都进球
D.甲队的表现时好时坏
6.(多选)如图是甲、乙两人在射击测试中6次命中环数的折线图,下列说法正确的是( )
A.若甲、乙射击成绩的平均数分别为1,2,则1>2
B.若甲、乙射击成绩的方差分别为s,s,则sC.乙射击成绩的中位数小于甲射击成绩的中位数
D.乙比甲的射击成绩稳定
7.已知五个数2,2,3,3,a的平均数是3,这五个数的方差是________.
8.甲、乙、丙、丁四人参加某运动会射击项目选拔赛,四人的平均成绩和方差如下表所示:
甲 乙 丙 丁
平均环数 8.3 8.8 8.8 8.7
方差s2 3.5 3.6 2.2 5.4
若要从这四人中选择一人去参加该运动会射击项目比赛,最佳人选是________.(填“甲”“乙”“丙”或“丁”)
9.从甲、乙两人中选拔一人参加射击比赛,对他们的射击水平进行了测试,两人在相同条件下各射击10次,命中的环数如下:
甲:7 8 6 8 6 5 9 10 7 4
乙:9 5 7 8 7 6 8 6 7 7
(1)分别计算甲、乙两人射击命中环数的平均数.
(2)选派谁去参赛更好?请说明理由.
10.某培训机构在假期招收了A,B两个数学补习班,A班10人,B班30人,经过一周的补习后进行了一次测试,在该测试中,A班的平均成绩为130分,方差为115,B班的平均成绩为110分,方差为215.求在这次测试中全体学生的平均成绩和方差.
能力提升
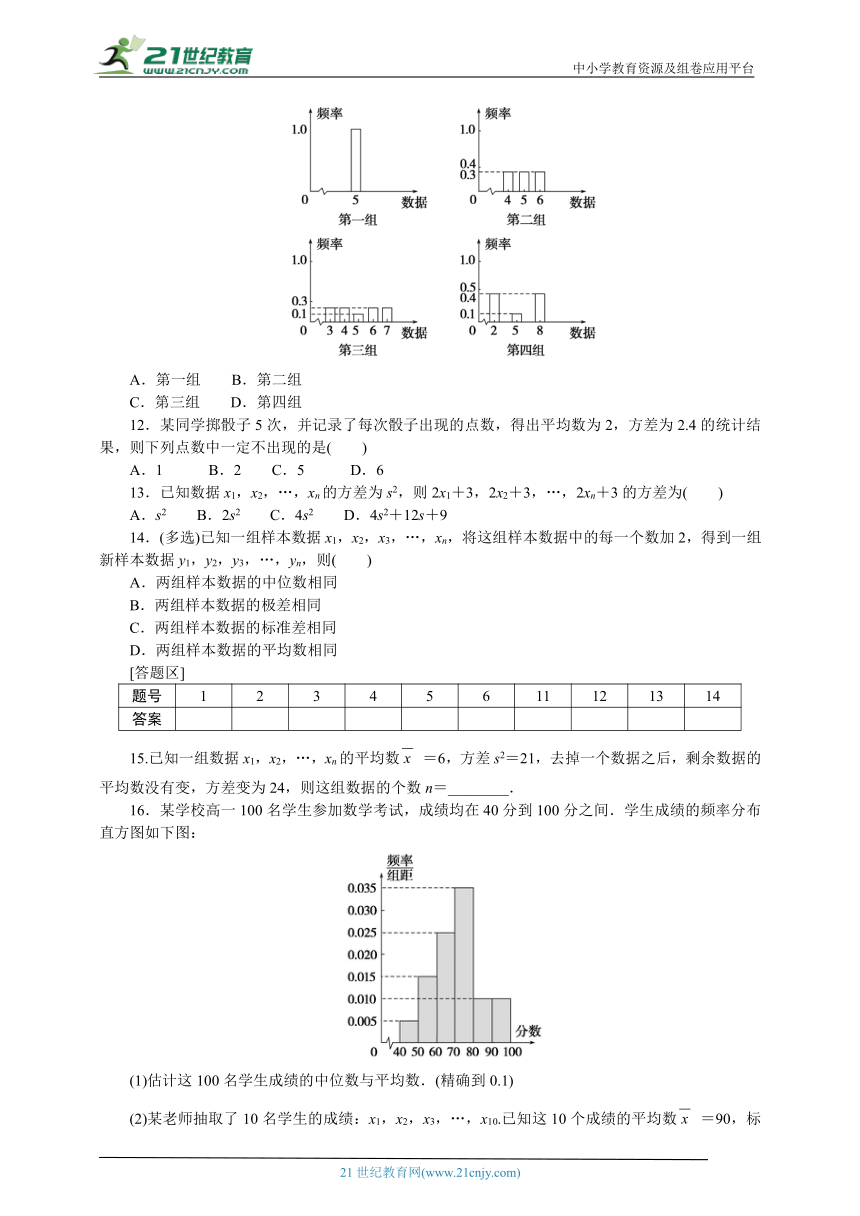
11.样本数为9的四组数据,它们的平均数都是5,条形图如图所示,则标准差最大的一组是( )
A.第一组 B.第二组
C.第三组 D.第四组
12.某同学掷骰子5次,并记录了每次骰子出现的点数,得出平均数为2,方差为2.4的统计结果,则下列点数中一定不出现的是( )
A.1 B.2 C.5 D.6
13.已知数据x1,x2,…,xn的方差为s2,则2x1+3,2x2+3,…,2xn+3的方差为( )
A.s2 B.2s2 C.4s2 D.4s2+12s+9
14.(多选)已知一组样本数据x1,x2,x3,…,xn,将这组样本数据中的每一个数加2,得到一组新样本数据y1,y2,y3,…,yn,则( )
A.两组样本数据的中位数相同
B.两组样本数据的极差相同
C.两组样本数据的标准差相同
D.两组样本数据的平均数相同
[答题区]
题号 1 2 3 4 5 6 11 12 13 14
答案
15.已知一组数据x1,x2,…,xn的平均数=6,方差s2=21,去掉一个数据之后,剩余数据的平均数没有变,方差变为24,则这组数据的个数n=________.
16.某学校高一100名学生参加数学考试,成绩均在40分到100分之间.学生成绩的频率分布直方图如下图:
(1)估计这100名学生成绩的中位数与平均数.(精确到0.1)
(2)某老师抽取了10名学生的成绩:x1,x2,x3,…,x10.已知这10个成绩的平均数=90,标准差s=6,若剔除其中的100和80两个成绩,求剩余8个成绩的平均数与标准差.
参考数据:2102=44 100,1922=36 864,1102=12 100
9.2.4 总体离散程度的估计
1.解析:A.在两组数据中,平均数与方差所表示的意义不同,由此不能根据平均数的大小来衡量其方差的大小,所以A的说法错误;C.求和后还需再平均,故C的说法错误;D.方差大的表示射击水平不稳定,故D的说法错误;只有B正确.故选B.
答案:B
2.解析:因为这组数据的平均数==8,所以这组数据的方差为
=4,标准差是2.故选C.
答案:C
3.解析:由题意可知两个班的数学成绩平均数为=甲=乙,则两个班数学成绩的方差为s2=×(20×2+30×3)=2.6.故选C.
答案:C
4.解析:由题意可知这25名学生成绩的平均数为=87,这25名学生成绩的方差为=10.2.故选A.
答案:A
5.解析:因为甲队平均每场进球数为3.2,乙队平均每场进球数为1.8,甲队平均数大于乙队较多,所以甲队技术比乙队好,所以A不正确;因为甲队全年比赛进球数的标准差为3,乙队全年进球数的标准差为0.3,乙队的标准差小于甲队,所以乙队发挥比甲队稳定,所以B正确;因为乙队的标准差为0.3,说明每次进球数均值,乙队几乎每场都进球,甲队标准差为3,说明甲队表现时好时坏,所以C,D正确.故选BCD.
答案:BCD
6.解析:由题图可知甲的射击成绩为9,10,6,7,9,8,乙的射击成绩为6,7,5,5,7,7.对于A,1=×(9+10+6+7+9+8)=,2=×(6+7+5+5+7+7)=,所以1>2,所以A正确;对于B,从甲、乙射击成绩看,甲的成绩比较分散,而乙的成绩比较集中,所以甲的方差较大,即s>s,所以B错误;对于C,甲的射击成绩排列后为6,7,8,9,9,10,则中位数为8.5,乙的射击成绩排列后为5,5,6,7,7,7,则中位数为6.5,所以乙射击成绩的中位数小于甲射击成绩的中位数,所以C正确;对于D,因为乙的成绩比较集中,所以乙比甲的射击成绩稳定,所以D正确.故选ACD.
答案:ACD
7.解析:依题意=3,解得a=5,所以方差为×[(2-3)2+(2-3)2+(3-3)2+(3-3)2+(5-3)2]=.
答案:
8.解析:首先乙、丙的平均数最高,乙、丙两人中,丙的方差较小,所以最佳人选是丙.
答案:丙
9.解析:(1)由题设,甲的平均数为
1==7,
乙的平均数为2==7.
由(1)知1=2,而s>s,
所以选派乙去参赛更好.
10.解析:依题意A=130,s=115,
B=110,s=215,
∴=×130+×110=115,
∴全体学生的平均成绩为115分.
全体学生成绩的方差为
s2=wA[s+(A-)2]+wB[s+(B-)2]
=×(115+225)+×(215+25)
=85+180=265.
11.解析:第一组中,样本数据都为5,数据没有波动幅度,标准差为0;第二组中,样本数据为4,4,4,5,5,5,6,6,6,标准差为;第三组中,样本数据为3,3,4,4,5,6,6,7,7,标准差为;第四组中,样本数据为2,2,2,2,5,8,8,8,8,标准差为2.故标准差最大的一组是第四组.故选D.
答案:D
12.解析:因为=3.2,根据方差的计算公式知,方差大于2.4,因此不能出现点数6,因为=1.8<2.4,=0<2.4,=0.2<2.4,则其余的点数1,2,5都有可能.故选D.
答案:D
13.解析:因为数据x1,x2,…,xn的方差为s2,则2x1+3,2x2+3,…,2xn+3的方差为22s2=4s2.故选C.
答案:C
14.解析:对于A,设原样本数据的中位数为M,则新样本数据的中位数为M+2,故A错误;对于B,不妨设原样本数据最大为xn,最小为x1,则原样本数据中,样本数据的极差为xn-x1,新样本数据中,样本数据的极差为(xn+2)-(x1+2)=xn-x1,故B正确;对于D,原样本数据的样本平均数为=(x1+x2+…+xn),新样本数据的样本平均数为=(x1+2+x2+2+…+xn+2)=+2,故D错误;对于C,原样本数据的标准差为
s= ,
新样本数据的标准差为
s′==s,故C正确.故选BC.
答案:BC
15.解析:因为去掉一个数据之后,数据的平均数没有变,所以去掉的数据为6,
去掉6后方差变为24,故得到24(n-1)=21n,解得n=8.
答案:8
16.解析:(1)因为0.05+0.15+0.25=0.45<0.5,
0.05+0.15+0.25+0.35=0.8>0.5,
所以中位数为x满足70由()×0.35+0.1+0.1=0.5,
解得x=80-≈71.4.
设平均分为y,
则y=0.05×45+0.15×55+0.25×65+0.35×75+0.1×85+0.1×95=71.0.
(2)由题意,剩余8个成绩的平均数为0==90,
因为10个成绩的标准差
所以x+…+x=10×62+10×902=81 360,
所以剩余8个成绩的标准差为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
9.2.4 总体离散程度的估计
基础强化
1.下列说法正确的是( )
A.在两组数据中,平均数较大的一组方差较大
B.平均数反映数据的集中趋势,方差则反映数据离平均数波动的幅度大小
C.方差的求法是求出各个数据与平均数的差的平方后再求和
D.在记录两个人射击环数的两组数据中,方差大的表示射击水平高
2.数据5,7,7,8,10,11的标准差是( )
A.8 B.4
C.2 D.1
3.在高一期中考试中,甲、乙两个班的数学成绩统计如下表:
班级 人数 平均分数 方差
甲 20 甲 2
乙 30 乙 3
其中甲=乙,则两个班数学成绩的方差为( )
A.3 B.2 C.2.6 D.2.5
4.某校为调查高一年级的某次考试的数学成绩情况,随机调查高一年级甲班10名学生,成绩的平均数为90,方差为3,乙班15名学生,成绩的平均数为85,方差为5,则这25名学生成绩的平均数和方差分别为( )
A.87,10.2 B.85,10.2 C.87,10 D.85,10
5.(多选)甲、乙两支女子曲棍球队在去年的国际联赛中,甲队平均每场的进球数是3.2,全年进球数的标准差为3;乙队平均每场的进球数是1.8,全年进球数的标准差为0.3.下列说法中正确的是( )
A.乙队的技术比甲队好
B.乙队发挥比甲队稳定
C.乙队几乎每场都进球
D.甲队的表现时好时坏
6.(多选)如图是甲、乙两人在射击测试中6次命中环数的折线图,下列说法正确的是( )
A.若甲、乙射击成绩的平均数分别为1,2,则1>2
B.若甲、乙射击成绩的方差分别为s,s,则s
D.乙比甲的射击成绩稳定
7.已知五个数2,2,3,3,a的平均数是3,这五个数的方差是________.
8.甲、乙、丙、丁四人参加某运动会射击项目选拔赛,四人的平均成绩和方差如下表所示:
甲 乙 丙 丁
平均环数 8.3 8.8 8.8 8.7
方差s2 3.5 3.6 2.2 5.4
若要从这四人中选择一人去参加该运动会射击项目比赛,最佳人选是________.(填“甲”“乙”“丙”或“丁”)
9.从甲、乙两人中选拔一人参加射击比赛,对他们的射击水平进行了测试,两人在相同条件下各射击10次,命中的环数如下:
甲:7 8 6 8 6 5 9 10 7 4
乙:9 5 7 8 7 6 8 6 7 7
(1)分别计算甲、乙两人射击命中环数的平均数.
(2)选派谁去参赛更好?请说明理由.
10.某培训机构在假期招收了A,B两个数学补习班,A班10人,B班30人,经过一周的补习后进行了一次测试,在该测试中,A班的平均成绩为130分,方差为115,B班的平均成绩为110分,方差为215.求在这次测试中全体学生的平均成绩和方差.
能力提升
11.样本数为9的四组数据,它们的平均数都是5,条形图如图所示,则标准差最大的一组是( )
A.第一组 B.第二组
C.第三组 D.第四组
12.某同学掷骰子5次,并记录了每次骰子出现的点数,得出平均数为2,方差为2.4的统计结果,则下列点数中一定不出现的是( )
A.1 B.2 C.5 D.6
13.已知数据x1,x2,…,xn的方差为s2,则2x1+3,2x2+3,…,2xn+3的方差为( )
A.s2 B.2s2 C.4s2 D.4s2+12s+9
14.(多选)已知一组样本数据x1,x2,x3,…,xn,将这组样本数据中的每一个数加2,得到一组新样本数据y1,y2,y3,…,yn,则( )
A.两组样本数据的中位数相同
B.两组样本数据的极差相同
C.两组样本数据的标准差相同
D.两组样本数据的平均数相同
[答题区]
题号 1 2 3 4 5 6 11 12 13 14
答案
15.已知一组数据x1,x2,…,xn的平均数=6,方差s2=21,去掉一个数据之后,剩余数据的平均数没有变,方差变为24,则这组数据的个数n=________.
16.某学校高一100名学生参加数学考试,成绩均在40分到100分之间.学生成绩的频率分布直方图如下图:
(1)估计这100名学生成绩的中位数与平均数.(精确到0.1)
(2)某老师抽取了10名学生的成绩:x1,x2,x3,…,x10.已知这10个成绩的平均数=90,标准差s=6,若剔除其中的100和80两个成绩,求剩余8个成绩的平均数与标准差.
参考数据:2102=44 100,1922=36 864,1102=12 100
9.2.4 总体离散程度的估计
1.解析:A.在两组数据中,平均数与方差所表示的意义不同,由此不能根据平均数的大小来衡量其方差的大小,所以A的说法错误;C.求和后还需再平均,故C的说法错误;D.方差大的表示射击水平不稳定,故D的说法错误;只有B正确.故选B.
答案:B
2.解析:因为这组数据的平均数==8,所以这组数据的方差为
=4,标准差是2.故选C.
答案:C
3.解析:由题意可知两个班的数学成绩平均数为=甲=乙,则两个班数学成绩的方差为s2=×(20×2+30×3)=2.6.故选C.
答案:C
4.解析:由题意可知这25名学生成绩的平均数为=87,这25名学生成绩的方差为=10.2.故选A.
答案:A
5.解析:因为甲队平均每场进球数为3.2,乙队平均每场进球数为1.8,甲队平均数大于乙队较多,所以甲队技术比乙队好,所以A不正确;因为甲队全年比赛进球数的标准差为3,乙队全年进球数的标准差为0.3,乙队的标准差小于甲队,所以乙队发挥比甲队稳定,所以B正确;因为乙队的标准差为0.3,说明每次进球数均值,乙队几乎每场都进球,甲队标准差为3,说明甲队表现时好时坏,所以C,D正确.故选BCD.
答案:BCD
6.解析:由题图可知甲的射击成绩为9,10,6,7,9,8,乙的射击成绩为6,7,5,5,7,7.对于A,1=×(9+10+6+7+9+8)=,2=×(6+7+5+5+7+7)=,所以1>2,所以A正确;对于B,从甲、乙射击成绩看,甲的成绩比较分散,而乙的成绩比较集中,所以甲的方差较大,即s>s,所以B错误;对于C,甲的射击成绩排列后为6,7,8,9,9,10,则中位数为8.5,乙的射击成绩排列后为5,5,6,7,7,7,则中位数为6.5,所以乙射击成绩的中位数小于甲射击成绩的中位数,所以C正确;对于D,因为乙的成绩比较集中,所以乙比甲的射击成绩稳定,所以D正确.故选ACD.
答案:ACD
7.解析:依题意=3,解得a=5,所以方差为×[(2-3)2+(2-3)2+(3-3)2+(3-3)2+(5-3)2]=.
答案:
8.解析:首先乙、丙的平均数最高,乙、丙两人中,丙的方差较小,所以最佳人选是丙.
答案:丙
9.解析:(1)由题设,甲的平均数为
1==7,
乙的平均数为2==7.
由(1)知1=2,而s>s,
所以选派乙去参赛更好.
10.解析:依题意A=130,s=115,
B=110,s=215,
∴=×130+×110=115,
∴全体学生的平均成绩为115分.
全体学生成绩的方差为
s2=wA[s+(A-)2]+wB[s+(B-)2]
=×(115+225)+×(215+25)
=85+180=265.
11.解析:第一组中,样本数据都为5,数据没有波动幅度,标准差为0;第二组中,样本数据为4,4,4,5,5,5,6,6,6,标准差为;第三组中,样本数据为3,3,4,4,5,6,6,7,7,标准差为;第四组中,样本数据为2,2,2,2,5,8,8,8,8,标准差为2.故标准差最大的一组是第四组.故选D.
答案:D
12.解析:因为=3.2,根据方差的计算公式知,方差大于2.4,因此不能出现点数6,因为=1.8<2.4,=0<2.4,=0.2<2.4,则其余的点数1,2,5都有可能.故选D.
答案:D
13.解析:因为数据x1,x2,…,xn的方差为s2,则2x1+3,2x2+3,…,2xn+3的方差为22s2=4s2.故选C.
答案:C
14.解析:对于A,设原样本数据的中位数为M,则新样本数据的中位数为M+2,故A错误;对于B,不妨设原样本数据最大为xn,最小为x1,则原样本数据中,样本数据的极差为xn-x1,新样本数据中,样本数据的极差为(xn+2)-(x1+2)=xn-x1,故B正确;对于D,原样本数据的样本平均数为=(x1+x2+…+xn),新样本数据的样本平均数为=(x1+2+x2+2+…+xn+2)=+2,故D错误;对于C,原样本数据的标准差为
s= ,
新样本数据的标准差为
s′==s,故C正确.故选BC.
答案:BC
15.解析:因为去掉一个数据之后,数据的平均数没有变,所以去掉的数据为6,
去掉6后方差变为24,故得到24(n-1)=21n,解得n=8.
答案:8
16.解析:(1)因为0.05+0.15+0.25=0.45<0.5,
0.05+0.15+0.25+0.35=0.8>0.5,
所以中位数为x满足70
解得x=80-≈71.4.
设平均分为y,
则y=0.05×45+0.15×55+0.25×65+0.35×75+0.1×85+0.1×95=71.0.
(2)由题意,剩余8个成绩的平均数为0==90,
因为10个成绩的标准差
所以x+…+x=10×62+10×902=81 360,
所以剩余8个成绩的标准差为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
