第八章单元测试卷(含解析)--人教A版(2019)高数必修二
文档属性
| 名称 | 第八章单元测试卷(含解析)--人教A版(2019)高数必修二 |  | |
| 格式 | docx | ||
| 文件大小 | 813.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 11:27:02 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第八章 单元测试卷
(时间:120分钟 满分:150分)
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.下列说法正确的是( )
A.三点可以确定一个平面 B.一条直线和一个点可以确定一个平面
C.四边形一定是平面图形 D.两条相交直线可以确定一个平面
2.如图,△ABC是水平放置的△ABC的斜二测直观图,其中O′C′=O′A′=2O′B′,则以下说法正确的是( )
A.△ABC是钝角三角形
B.△ABC是等边三角形
C.△ABC是等腰直角三角形
D.△ABC是等腰三角形,但不是直角三角形
3.已知α,β是两个不同的平面,l,m是两条不同的直线,则下列说法错误的是( )
A.若l⊥α,m⊥α,则l∥m
B.若l∥α,α∥β,则l∥β
C.若l∥α,l β,α∩β=m,则l∥m
D.若l与m异面,l α,l∥β,m β,m∥α,则α∥β
4.已知平面α,β,γ两两垂直,直线a,b,c满足a α,b β,c γ,则直线a,b,c不可能满足以下哪种关系( )
A.两两垂直 B.两两平行
C.两两相交 D.两两异面
5.如图,在正四面体ABCD中,M是BC的中点,P是线段AM上的动点,则直线DP和BC所成角的大小( )
A.一定为90° B.一定为60°
C.一定为45° D.与P的位置有关
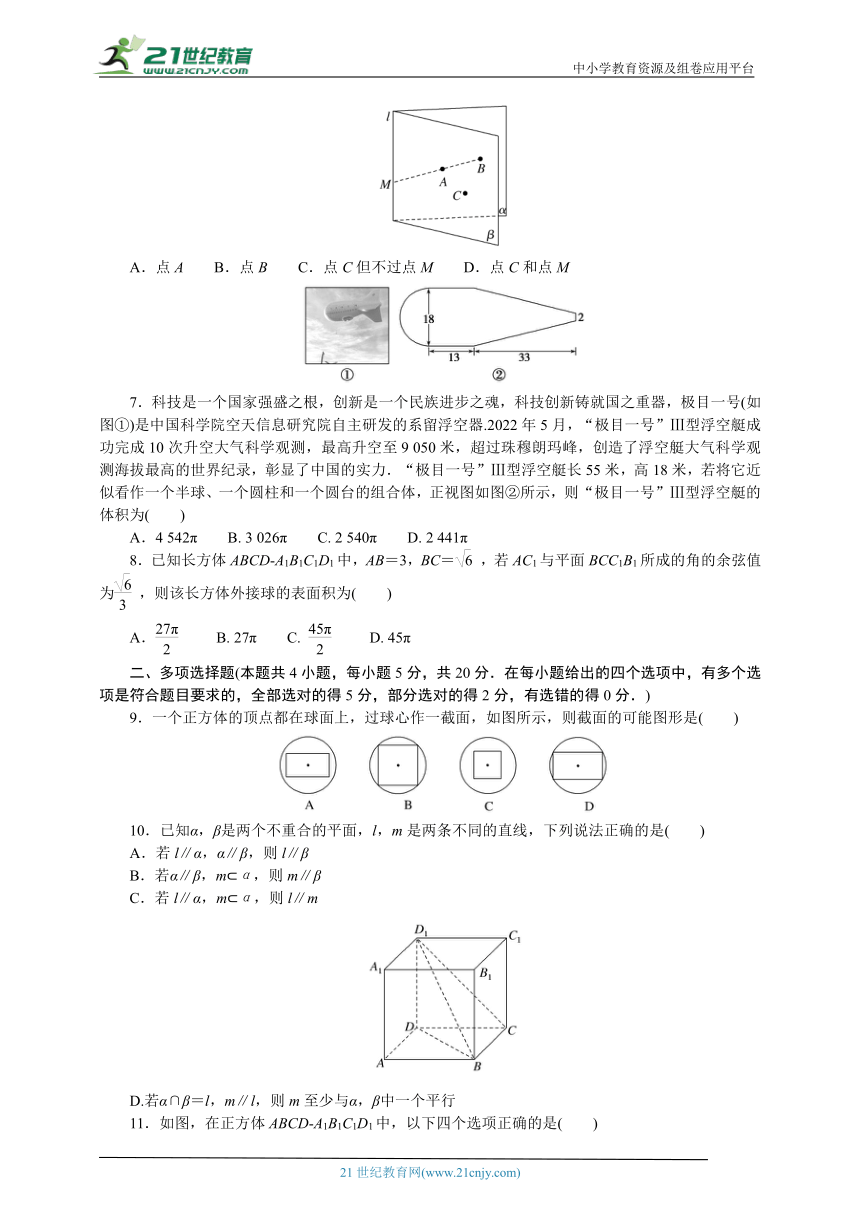
6.如图,α∩β=l,A,B∈α,C∈β,且C l,直线AB∩l=M,过A,B,C三点的平面记作γ,则γ与β的交线必通过( )
A.点A B.点B C.点C但不过点M D.点C和点M
7.科技是一个国家强盛之根,创新是一个民族进步之魂,科技创新铸就国之重器,极目一号(如图①)是中国科学院空天信息研究院自主研发的系留浮空器.2022年5月,“极目一号”Ⅲ型浮空艇成功完成10次升空大气科学观测,最高升空至9 050米,超过珠穆朗玛峰,创造了浮空艇大气科学观测海拔最高的世界纪录,彰显了中国的实力.“极目一号”Ⅲ型浮空艇长55米,高18米,若将它近似看作一个半球、一个圆柱和一个圆台的组合体,正视图如图②所示,则“极目一号”Ⅲ型浮空艇的体积为( )
A.4 542π B. 3 026π C. 2 540π D. 2 441π
8.已知长方体ABCD A1B1C1D1中,AB=3,BC=,若AC1与平面BCC1B1所成的角的余弦值为,则该长方体外接球的表面积为( )
A. B. 27π C. D. 45π
二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项是符合题目要求的,全部选对的得5分,部分选对的得2分,有选错的得0分.)
9.一个正方体的顶点都在球面上,过球心作一截面,如图所示,则截面的可能图形是( )
10.已知α,β是两个不重合的平面,l,m是两条不同的直线,下列说法正确的是( )
A.若l∥α,α∥β,则l∥β
B.若α∥β,m α,则m∥β
C.若l∥α,m α,则l∥m
D.若α∩β=l,m∥l,则m至少与α,β中一个平行
11.如图,在正方体ABCD A1B1C1D1中,以下四个选项正确的是( )
A.D1C∥平面A1ABB1
B.A1D1与平面BCD1相交
C.AD⊥平面D1DB
D.平面BCD1⊥平面A1ABB1
12.如图,正四棱柱ABCD A1B1C1D1中,AA1=2AB,E,F分别为CC1,AA1的中点,则下列结论错误的是( )
A.B1E⊥平面BEF
B.直线B1E与直线BF所成的角为90°
C.平面BEF与平面ABCD的夹角为45°
D.直线D1F与平面ABCD所成的角为45°
三、填空题(本题共4小题,每小题5分,共20分.)
13.已知圆台的上底面半径为2,下底面半径为6,若该圆台的侧面积为72π,则其母线长为________.
14.如图,在直二面角α AB β中,AC和BD分别在平面α和β上,它们都垂直于AB,且AB=4,AC=6,BD=8,则CD=________.
15.已知正方体ABCD A1B1C1D1的棱长为3,则C1到平面A1BD的距离为________.
16.已知三棱锥P ABC的棱长均为1,先在三棱锥P ABC内放入一个内切球O1,然后再放入一个球O2,使得球O2与球O1与三棱锥P ABC的三个侧面都相切,则球O1的半径为________,球O2的体积为________.
四、解答题(本题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤.)
17.(本小题10分)(1)已知正四棱锥的底面边长是6,侧棱长为5,求该正四棱锥的表面积.
(2)在△ABC中,∠C=90°,∠A=30°,BC=1.在三角形内挖去半圆形(圆心O在边AC上,半圆形与BC、AB分别相切于点C、M,与AC交于N),求图中阴影部分绕直线AC旋转一周所得的几何体体积.
18.(本小题12分)如图,在四棱锥P ABCD中,四边形ABCD是菱形,PA=PC,E为PB的中点.求证:
(1)PD∥平面AEC;
(2)平面AEC⊥平面PBD.
19.(本小题12分)如图,在三棱柱A1B1C1 ABC中,E,F,G,H分别为BB1,CC1,A1B1,A1C1的中点.
(1)证明:E,F,G,H四点共面.
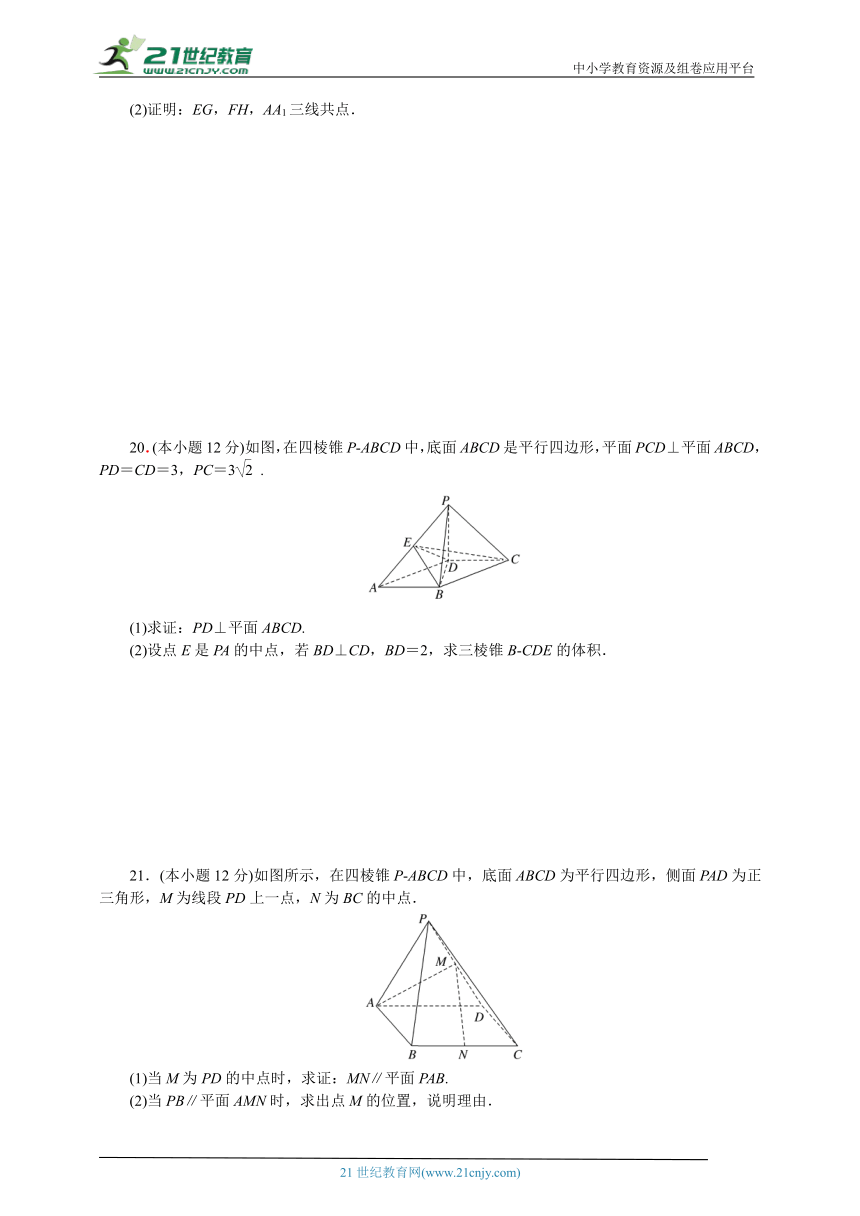
(2)证明:EG,FH,AA1三线共点.
20.(本小题12分)如图,在四棱锥P ABCD中,底面ABCD是平行四边形,平面PCD⊥平面ABCD,PD=CD=3,PC=3.
(1)求证:PD⊥平面ABCD.
(2)设点E是PA的中点,若BD⊥CD,BD=2,求三棱锥B CDE的体积.
21.(本小题12分)如图所示,在四棱锥P ABCD中,底面ABCD为平行四边形,侧面PAD为正三角形,M为线段PD上一点,N为BC的中点.
(1)当M为PD的中点时,求证:MN∥平面PAB.
(2)当PB∥平面AMN时,求出点M的位置,说明理由.
22.(本小题12分)平行四边形ABCD中,AB=2AD=2,DB=,如图甲所示,作DE⊥AB于点E,将△ADE沿着DE翻折,使点A与点P重合,如图乙所示.
(1)设平面PEB与平面PDC的交线为l,判断l与CD的位置关系,并证明;
(2)当四棱锥P BCDE的体积最大时,求二面角P BC D的正切值;
(3)在(2)的条件下,G、H分别为棱DE,CD上的点,求空间四边形PGHB周长的最小值.
第八章 单元测试卷
1.解析:A错误,不共线的三点可以确定一个平面;B错误,一条直线和直线外一个点可以确定一个平面;C错误,四边形不一定是平面图形,比如空间四边形;D正确,两条相交直线可以确定一个平面.故选D.
答案:D
2.解析:将其还原成原图,如图,设A′C′=2,则可得OB=2O′B′=1,AC=A′C′=2,从而AB=BC=,所以AB2+BC2=AC2,即AB⊥BC,故△ABC是等腰直角三角形.故选C.
答案:C
3.解析:对于A,根据垂直于同一平面的两条直线平行可知A正确;对于B,若l∥α,α∥β,则l∥β或l β,故B错误;对于C,根据直线与平面平行的性质定理可知C正确;对于D,假设α∩β=n,因为l α,l∥β,α∩β=n,所以l∥n,同理可得m∥n,所以l∥m,这与l与m异面相矛盾,故假设不成立,则α∥β,故D正确.故选B.
答案:B
4.解析:设α∩β=l,且l与a,b均不重合,假设a∥b∥c,由a∥b可得a∥β,b∥α,又α∩β=l,可知a∥l,b∥l,又a∥b∥c,可得c∥l.因为α,β,γ两两互相垂直,所以l与γ相交,即l与c相交或异面.若l与a或b重合,同理可得l与c相交或异面,可知假设错误,由此可知三条直线不能两两平行.故选B.
答案:B
5.解析:连接DM,
∵四面体ABCD是正四面体,M是BC的中点,∴△DBC、△ABC是等边三角形,∴BC⊥DM,BC⊥PM.∵DM 平面DMP,PM 平面DMP,DM∩PM=M,∴BC⊥平面DMP,又DP 平面DMP,∴BC⊥DP,∴直线DP与BC所成角为90°.故选A.
答案:A
6.解析:对于A、B,易得A,B β,故必不在γ与β的交线上,故A、B错误;对于C、D,因为过A,B,C三点的平面记作γ,所以平面ABC与γ是同一个面,因为直线AB∩l=M,所以M∈AB 平面ABC,则M∈γ,又C∈平面ABC,则C∈γ,所以MC γ;因为AB∩l=M,α∩β=l,所以M∈l β,又C∈β,所以MC β,所以β∩γ=MC,所以γ与β的交线必通过点C和点M.故C错误,D正确.故选D.
答案:D
7.解析:该组合体的直观图如图.
半球的半径为9米,圆柱的底面半径为9米,母线长为13米,圆台的两底面半径分别为9米和1米,高为33米,所以半球的体积为×π·93=486π(立方米),圆柱的体积为π·92·13=1 053π(立方米),圆台的体积为×33π(92+9×1+12)=1 001π(立方米),故该组合体的体积为486π+1 053π+1 001π=2 540π(立方米).故选C.
答案:C
8.
解析:连BC1,因为AB⊥平面BCC1B1,所以∠AC1B是AC1与平面BCC1B1所成的角,所以cos ∠AC1B==,所以AC1=,设CC1=x,则BC=BC2+CC,即BC=6+x2, 又AC=AB2+BC2+CC,所以=9+6+x2,所以=15+x2,即x2=12,所以BC=18,AC==27,因为该长方体外接球的直径是AC1,设半径为R,则R2=AC=,所以该外接球的表面积为4πR2=4π·=27π.故选B.
答案:B
9.解析:当截面平行于正方体的一个侧面时得C;当截面过正方体的体对角线时可得D;当截面既不过体对角线又不与任一侧面平行时,可得A;但无论如何都不能截得B.故选ACD.
答案:ACD
10.解析:A.如图所示:可得结果l∥β或l β,故A错误;
B.如图所示:,可得结果m∥β,故B正确;
C.如图所示:,可得m⊥l,故C错误;
D.如图所示:,可得结果m∥α或m∥β,故D正确.故选BD.
答案:BD
11.解析:对于A,因为平面A1ABB1∥平面D1DCC1,而D1C 平面D1DCC1,故D1C与平面A1ABB1没有公共点,所以D1C∥平面A1ABB1,即A正确;对于B,因为A1D1∥BC,所以A1D1 平面BCD1,所以B错误;对于C,若AD⊥平面D1DB,则AD⊥DB,但∠ADB=45°,所以C错误;对于D,在正方体ABCD A1B1C1D1中,易得BC⊥平面A1ABB1,而BC 平面BCD1,所以平面BCD1⊥平面A1ABB1,所以D正确.故选AD.
答案:AD
12.解析:
对于A,如图,连接B1F,由题意A1B1=B1C1,又E,F分别为CC1,AA1的中点,可得B1E=B1F,若B1E⊥平面BEF,则B1E⊥EF,进而∠B1EF=∠B1FE=90°.这显然不成立,故B1E与平面BEF不垂直,A错误.对于B,假设直线B1E与直线BF所成的角为90°,即B1E⊥BF,由正四棱柱的性质可知B1A1⊥平面B1BCC1,而B1E 平面B1BCC1,所以B1A1⊥B1E,可得B1E⊥平面ABB1A1,而由正四棱柱的性质可知B1C1⊥平面ABB1A1,所以B1E∥B1C1,显然这是不可能的,所以假设不成立,因此B错误.对于C,分别延长D1F,DA交于点P,连接PB,则直线PB即为平面BED1F与平面ABCD的交线.连接BD,BD1,可证PB⊥平面BDD1,故∠DBD1即为平面BEF与平面ABCD的夹角,易知tan ∠DBD1==>1,故∠DBD1>45°,C错误.对于D,可证D1F∥BE,则直线D1F与平面ABCD所成的角为∠EBC,又根据题意易知∠EBC=45°,D正确.故选ABC.
答案:ABC
13.解析:圆台的上底面半径为2,下底面半径为6,设圆台的母线长为l,则该圆台的侧面积为S侧=π×(2+6)×l=72π,则l=9,所以圆台的母线长为9.
答案:9
14.解析:连接BC,在直二面角α AB β中BD⊥AB,α∩β=AB,BD β,所以BD⊥α,又BC α,则BD⊥BC,又AC⊥AB,
所以,在Rt△ABC、Rt△DBC中CD==2.
答案:2
15.解析:连接AC1,AD1,可以证明A1D⊥平面AC1D1,得AC1⊥A1D.同理可得AC1⊥A1B,故AC1⊥平面A1BD.连接AC交BD于O,连接A1O交AC1于点E,可以证明△AOE∽△C1A1E,则==,所以C1E=AC1=2,即C1到平面A1BD的距离为2.
答案:2
16.
解析:如图所示.已知三棱锥P ABC的棱长均为1,所以三棱锥P ABC为正四面体,设底面三角形ABC中心为O,PO⊥底面ABC,则O1,O2在PO上,取BC的中点D,作截面PAD,球O1,球O2与PD切于N,E,连接O1N,O2E.由题意得S△ABC=×1×1×sin 60°= ,底面ABC的外接圆半径为2r1=== r1=,点P到平面ABC的距离为d= = ,所以VP-ABC=·S△ABC·h=××= , 所以S△PBC=S△PAB=S△PAC=×1×1×sin 60°=,设球O1的半径为R,所以VP ABC=+++,则=(×4)·R,得R= .设球O2的半径为r,则=,=,又R=,d=,得r=,所以球O2的体积为V=()3= .
答案:
17.解析:(1)正四棱锥P ABCD中,底面正方形ABCD的面积S1=AB2=36,在等腰△PAB中,PA=PB=5,AB=6,则边AB上的高h= =4,因此该正四棱锥的侧面积S2=4S△PAB=4×AB×h=2×6×4=48,
所以该正四棱锥的表面积S=S1+S2=36+48=84.
(2)几何体是图中阴影部分绕直线AC旋转一周所得旋转体,
是一个圆锥内挖去一个球后剩余部分,球是圆锥的内接球,
所以圆锥的底面半径是1,高为,
球的半径为r,tan 30°==,r=,
所以圆锥的体积为×12×π×=,
球的体积为π×()3=,
阴影部分绕直线AC旋转一周所得旋转体的体积为-=.
18.证明:(1)设AC∩BD=O,连接EO,如图所示.
因为O,E分别为BD,PB的中点,所以PD∥EO,
又因为PD 平面AEC,EO 平面AEC,
所以PD∥平面AEC.
(2)连接PO,如图所示.
因为PA=PC,O为AC的中点,所以AC⊥PO,
又因为四边形ABCD为菱形,所以AC⊥BD,
因为PO 平面PBD,BD 平面PBD,且PO∩BD=O,
所以AC⊥平面PBD,又因为AC 平面AEC,
所以平面AEC⊥平面PBD.
19.证明:(1)如图,连接EF,GH.
∵GH是△A1B1C1的中位线,∴GH∥B1C1.
∵B1E∥C1F,且B1E=C1F,∴四边形B1EFC1是平行四边形,
∴EF∥B1C1,∴EF∥GH,∴E,F,G,H四点共面.
(2)如图,延长EG,FH相交于点P.
∵P∈EG,EG 平面ABB1A1,∴P∈平面ABB1A1.
∵P∈FH,FH 平面ACC1A1,∴P∈平面ACC1A1.
∵平面ABB1A1∩平面ACC1A1=AA1,∴P∈AA1,
∴EG,FH,AA1三线共点.
20.解析:(1)证明:在△PDC中,PD=CD=3,PC=3,PD2+DC2=PC2,则PD⊥DC.
又平面PCD⊥平面ABCD,且平面PCD∩平面ABCD=CD,PD 平面PDC,故PD⊥平面ABCD.
(2)PD=3,点E是PA的中点,E到平面ABCD的距离d=PD=.
又BD⊥CD,BD=2,CD=3,S△BCD=×2×3=3.
VB CDE=VE BCD=·S△BCD·d=×3×=.
21.解析:(1)证明:取AP中点为E,连接EM,EB,
在△PAD中,M为PD的中点,E为AP中点,∴EM∥AD,EM=AD,
在平行四边形ABCD中,N为BC的中点,∴BN∥AD,BN=AD,
∴BN∥ME,BN=ME,∴四边形BNME为平行四边形,
∴MN∥BE,MN 平面PAB,BE 平面PAB,∴MN∥平面PAB.
(2)连接AN,BD,相交于O,连接OM,
∵PB∥平面AMN,平面PBD∩平面AMN=OM,PB 平面PBD,
∴PB∥OM,===,即存在点M,M为PD上靠近P点的三等分点.
22.解析:(1)l∥CD.证明:因为EB∥CD,CD 平面PBE,EB 平面PBE,所以CD∥平面PBE.
因为CD 平面PCD,平面PBE∩平面PCD=l,所以l∥CD.
(2)当平面PDE⊥平面BCDE时,四棱锥P BCDE的体积最大.
平面PDE∩平面BCDE=DE,PE 平面PDE,PE⊥DE,
可得PE⊥平面BCDE,BC 平面BCDE,可得PE⊥BC,
作EO⊥BC交BC于点O,连接PO,EO∩PE=E,
可得BC⊥平面POE,而PO在平面PEO中,故BC⊥PO,
∠POE即为二面角P BC D的平面角,
在Rt△POE中,PE=,EO=×sin 60°=,
tan ∠POE==,
所以二面角P BC D的正切值为.
(3)由展开图可知,B关于CD的对称点为B′,DE=,BB′=,由勾股定理可得AB′=,PB=,当A、G、H、B′共线时,周长最短,
此时(PG+GH+HB+PB)min=AB′+PB=+.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八章 单元测试卷
(时间:120分钟 满分:150分)
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.下列说法正确的是( )
A.三点可以确定一个平面 B.一条直线和一个点可以确定一个平面
C.四边形一定是平面图形 D.两条相交直线可以确定一个平面
2.如图,△ABC是水平放置的△ABC的斜二测直观图,其中O′C′=O′A′=2O′B′,则以下说法正确的是( )
A.△ABC是钝角三角形
B.△ABC是等边三角形
C.△ABC是等腰直角三角形
D.△ABC是等腰三角形,但不是直角三角形
3.已知α,β是两个不同的平面,l,m是两条不同的直线,则下列说法错误的是( )
A.若l⊥α,m⊥α,则l∥m
B.若l∥α,α∥β,则l∥β
C.若l∥α,l β,α∩β=m,则l∥m
D.若l与m异面,l α,l∥β,m β,m∥α,则α∥β
4.已知平面α,β,γ两两垂直,直线a,b,c满足a α,b β,c γ,则直线a,b,c不可能满足以下哪种关系( )
A.两两垂直 B.两两平行
C.两两相交 D.两两异面
5.如图,在正四面体ABCD中,M是BC的中点,P是线段AM上的动点,则直线DP和BC所成角的大小( )
A.一定为90° B.一定为60°
C.一定为45° D.与P的位置有关
6.如图,α∩β=l,A,B∈α,C∈β,且C l,直线AB∩l=M,过A,B,C三点的平面记作γ,则γ与β的交线必通过( )
A.点A B.点B C.点C但不过点M D.点C和点M
7.科技是一个国家强盛之根,创新是一个民族进步之魂,科技创新铸就国之重器,极目一号(如图①)是中国科学院空天信息研究院自主研发的系留浮空器.2022年5月,“极目一号”Ⅲ型浮空艇成功完成10次升空大气科学观测,最高升空至9 050米,超过珠穆朗玛峰,创造了浮空艇大气科学观测海拔最高的世界纪录,彰显了中国的实力.“极目一号”Ⅲ型浮空艇长55米,高18米,若将它近似看作一个半球、一个圆柱和一个圆台的组合体,正视图如图②所示,则“极目一号”Ⅲ型浮空艇的体积为( )
A.4 542π B. 3 026π C. 2 540π D. 2 441π
8.已知长方体ABCD A1B1C1D1中,AB=3,BC=,若AC1与平面BCC1B1所成的角的余弦值为,则该长方体外接球的表面积为( )
A. B. 27π C. D. 45π
二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项是符合题目要求的,全部选对的得5分,部分选对的得2分,有选错的得0分.)
9.一个正方体的顶点都在球面上,过球心作一截面,如图所示,则截面的可能图形是( )
10.已知α,β是两个不重合的平面,l,m是两条不同的直线,下列说法正确的是( )
A.若l∥α,α∥β,则l∥β
B.若α∥β,m α,则m∥β
C.若l∥α,m α,则l∥m
D.若α∩β=l,m∥l,则m至少与α,β中一个平行
11.如图,在正方体ABCD A1B1C1D1中,以下四个选项正确的是( )
A.D1C∥平面A1ABB1
B.A1D1与平面BCD1相交
C.AD⊥平面D1DB
D.平面BCD1⊥平面A1ABB1
12.如图,正四棱柱ABCD A1B1C1D1中,AA1=2AB,E,F分别为CC1,AA1的中点,则下列结论错误的是( )
A.B1E⊥平面BEF
B.直线B1E与直线BF所成的角为90°
C.平面BEF与平面ABCD的夹角为45°
D.直线D1F与平面ABCD所成的角为45°
三、填空题(本题共4小题,每小题5分,共20分.)
13.已知圆台的上底面半径为2,下底面半径为6,若该圆台的侧面积为72π,则其母线长为________.
14.如图,在直二面角α AB β中,AC和BD分别在平面α和β上,它们都垂直于AB,且AB=4,AC=6,BD=8,则CD=________.
15.已知正方体ABCD A1B1C1D1的棱长为3,则C1到平面A1BD的距离为________.
16.已知三棱锥P ABC的棱长均为1,先在三棱锥P ABC内放入一个内切球O1,然后再放入一个球O2,使得球O2与球O1与三棱锥P ABC的三个侧面都相切,则球O1的半径为________,球O2的体积为________.
四、解答题(本题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤.)
17.(本小题10分)(1)已知正四棱锥的底面边长是6,侧棱长为5,求该正四棱锥的表面积.
(2)在△ABC中,∠C=90°,∠A=30°,BC=1.在三角形内挖去半圆形(圆心O在边AC上,半圆形与BC、AB分别相切于点C、M,与AC交于N),求图中阴影部分绕直线AC旋转一周所得的几何体体积.
18.(本小题12分)如图,在四棱锥P ABCD中,四边形ABCD是菱形,PA=PC,E为PB的中点.求证:
(1)PD∥平面AEC;
(2)平面AEC⊥平面PBD.
19.(本小题12分)如图,在三棱柱A1B1C1 ABC中,E,F,G,H分别为BB1,CC1,A1B1,A1C1的中点.
(1)证明:E,F,G,H四点共面.
(2)证明:EG,FH,AA1三线共点.
20.(本小题12分)如图,在四棱锥P ABCD中,底面ABCD是平行四边形,平面PCD⊥平面ABCD,PD=CD=3,PC=3.
(1)求证:PD⊥平面ABCD.
(2)设点E是PA的中点,若BD⊥CD,BD=2,求三棱锥B CDE的体积.
21.(本小题12分)如图所示,在四棱锥P ABCD中,底面ABCD为平行四边形,侧面PAD为正三角形,M为线段PD上一点,N为BC的中点.
(1)当M为PD的中点时,求证:MN∥平面PAB.
(2)当PB∥平面AMN时,求出点M的位置,说明理由.
22.(本小题12分)平行四边形ABCD中,AB=2AD=2,DB=,如图甲所示,作DE⊥AB于点E,将△ADE沿着DE翻折,使点A与点P重合,如图乙所示.
(1)设平面PEB与平面PDC的交线为l,判断l与CD的位置关系,并证明;
(2)当四棱锥P BCDE的体积最大时,求二面角P BC D的正切值;
(3)在(2)的条件下,G、H分别为棱DE,CD上的点,求空间四边形PGHB周长的最小值.
第八章 单元测试卷
1.解析:A错误,不共线的三点可以确定一个平面;B错误,一条直线和直线外一个点可以确定一个平面;C错误,四边形不一定是平面图形,比如空间四边形;D正确,两条相交直线可以确定一个平面.故选D.
答案:D
2.解析:将其还原成原图,如图,设A′C′=2,则可得OB=2O′B′=1,AC=A′C′=2,从而AB=BC=,所以AB2+BC2=AC2,即AB⊥BC,故△ABC是等腰直角三角形.故选C.
答案:C
3.解析:对于A,根据垂直于同一平面的两条直线平行可知A正确;对于B,若l∥α,α∥β,则l∥β或l β,故B错误;对于C,根据直线与平面平行的性质定理可知C正确;对于D,假设α∩β=n,因为l α,l∥β,α∩β=n,所以l∥n,同理可得m∥n,所以l∥m,这与l与m异面相矛盾,故假设不成立,则α∥β,故D正确.故选B.
答案:B
4.解析:设α∩β=l,且l与a,b均不重合,假设a∥b∥c,由a∥b可得a∥β,b∥α,又α∩β=l,可知a∥l,b∥l,又a∥b∥c,可得c∥l.因为α,β,γ两两互相垂直,所以l与γ相交,即l与c相交或异面.若l与a或b重合,同理可得l与c相交或异面,可知假设错误,由此可知三条直线不能两两平行.故选B.
答案:B
5.解析:连接DM,
∵四面体ABCD是正四面体,M是BC的中点,∴△DBC、△ABC是等边三角形,∴BC⊥DM,BC⊥PM.∵DM 平面DMP,PM 平面DMP,DM∩PM=M,∴BC⊥平面DMP,又DP 平面DMP,∴BC⊥DP,∴直线DP与BC所成角为90°.故选A.
答案:A
6.解析:对于A、B,易得A,B β,故必不在γ与β的交线上,故A、B错误;对于C、D,因为过A,B,C三点的平面记作γ,所以平面ABC与γ是同一个面,因为直线AB∩l=M,所以M∈AB 平面ABC,则M∈γ,又C∈平面ABC,则C∈γ,所以MC γ;因为AB∩l=M,α∩β=l,所以M∈l β,又C∈β,所以MC β,所以β∩γ=MC,所以γ与β的交线必通过点C和点M.故C错误,D正确.故选D.
答案:D
7.解析:该组合体的直观图如图.
半球的半径为9米,圆柱的底面半径为9米,母线长为13米,圆台的两底面半径分别为9米和1米,高为33米,所以半球的体积为×π·93=486π(立方米),圆柱的体积为π·92·13=1 053π(立方米),圆台的体积为×33π(92+9×1+12)=1 001π(立方米),故该组合体的体积为486π+1 053π+1 001π=2 540π(立方米).故选C.
答案:C
8.
解析:连BC1,因为AB⊥平面BCC1B1,所以∠AC1B是AC1与平面BCC1B1所成的角,所以cos ∠AC1B==,所以AC1=,设CC1=x,则BC=BC2+CC,即BC=6+x2, 又AC=AB2+BC2+CC,所以=9+6+x2,所以=15+x2,即x2=12,所以BC=18,AC==27,因为该长方体外接球的直径是AC1,设半径为R,则R2=AC=,所以该外接球的表面积为4πR2=4π·=27π.故选B.
答案:B
9.解析:当截面平行于正方体的一个侧面时得C;当截面过正方体的体对角线时可得D;当截面既不过体对角线又不与任一侧面平行时,可得A;但无论如何都不能截得B.故选ACD.
答案:ACD
10.解析:A.如图所示:可得结果l∥β或l β,故A错误;
B.如图所示:,可得结果m∥β,故B正确;
C.如图所示:,可得m⊥l,故C错误;
D.如图所示:,可得结果m∥α或m∥β,故D正确.故选BD.
答案:BD
11.解析:对于A,因为平面A1ABB1∥平面D1DCC1,而D1C 平面D1DCC1,故D1C与平面A1ABB1没有公共点,所以D1C∥平面A1ABB1,即A正确;对于B,因为A1D1∥BC,所以A1D1 平面BCD1,所以B错误;对于C,若AD⊥平面D1DB,则AD⊥DB,但∠ADB=45°,所以C错误;对于D,在正方体ABCD A1B1C1D1中,易得BC⊥平面A1ABB1,而BC 平面BCD1,所以平面BCD1⊥平面A1ABB1,所以D正确.故选AD.
答案:AD
12.解析:
对于A,如图,连接B1F,由题意A1B1=B1C1,又E,F分别为CC1,AA1的中点,可得B1E=B1F,若B1E⊥平面BEF,则B1E⊥EF,进而∠B1EF=∠B1FE=90°.这显然不成立,故B1E与平面BEF不垂直,A错误.对于B,假设直线B1E与直线BF所成的角为90°,即B1E⊥BF,由正四棱柱的性质可知B1A1⊥平面B1BCC1,而B1E 平面B1BCC1,所以B1A1⊥B1E,可得B1E⊥平面ABB1A1,而由正四棱柱的性质可知B1C1⊥平面ABB1A1,所以B1E∥B1C1,显然这是不可能的,所以假设不成立,因此B错误.对于C,分别延长D1F,DA交于点P,连接PB,则直线PB即为平面BED1F与平面ABCD的交线.连接BD,BD1,可证PB⊥平面BDD1,故∠DBD1即为平面BEF与平面ABCD的夹角,易知tan ∠DBD1==>1,故∠DBD1>45°,C错误.对于D,可证D1F∥BE,则直线D1F与平面ABCD所成的角为∠EBC,又根据题意易知∠EBC=45°,D正确.故选ABC.
答案:ABC
13.解析:圆台的上底面半径为2,下底面半径为6,设圆台的母线长为l,则该圆台的侧面积为S侧=π×(2+6)×l=72π,则l=9,所以圆台的母线长为9.
答案:9
14.解析:连接BC,在直二面角α AB β中BD⊥AB,α∩β=AB,BD β,所以BD⊥α,又BC α,则BD⊥BC,又AC⊥AB,
所以,在Rt△ABC、Rt△DBC中CD==2.
答案:2
15.解析:连接AC1,AD1,可以证明A1D⊥平面AC1D1,得AC1⊥A1D.同理可得AC1⊥A1B,故AC1⊥平面A1BD.连接AC交BD于O,连接A1O交AC1于点E,可以证明△AOE∽△C1A1E,则==,所以C1E=AC1=2,即C1到平面A1BD的距离为2.
答案:2
16.
解析:如图所示.已知三棱锥P ABC的棱长均为1,所以三棱锥P ABC为正四面体,设底面三角形ABC中心为O,PO⊥底面ABC,则O1,O2在PO上,取BC的中点D,作截面PAD,球O1,球O2与PD切于N,E,连接O1N,O2E.由题意得S△ABC=×1×1×sin 60°= ,底面ABC的外接圆半径为2r1=== r1=,点P到平面ABC的距离为d= = ,所以VP-ABC=·S△ABC·h=××= , 所以S△PBC=S△PAB=S△PAC=×1×1×sin 60°=,设球O1的半径为R,所以VP ABC=+++,则=(×4)·R,得R= .设球O2的半径为r,则=,=,又R=,d=,得r=,所以球O2的体积为V=()3= .
答案:
17.解析:(1)正四棱锥P ABCD中,底面正方形ABCD的面积S1=AB2=36,在等腰△PAB中,PA=PB=5,AB=6,则边AB上的高h= =4,因此该正四棱锥的侧面积S2=4S△PAB=4×AB×h=2×6×4=48,
所以该正四棱锥的表面积S=S1+S2=36+48=84.
(2)几何体是图中阴影部分绕直线AC旋转一周所得旋转体,
是一个圆锥内挖去一个球后剩余部分,球是圆锥的内接球,
所以圆锥的底面半径是1,高为,
球的半径为r,tan 30°==,r=,
所以圆锥的体积为×12×π×=,
球的体积为π×()3=,
阴影部分绕直线AC旋转一周所得旋转体的体积为-=.
18.证明:(1)设AC∩BD=O,连接EO,如图所示.
因为O,E分别为BD,PB的中点,所以PD∥EO,
又因为PD 平面AEC,EO 平面AEC,
所以PD∥平面AEC.
(2)连接PO,如图所示.
因为PA=PC,O为AC的中点,所以AC⊥PO,
又因为四边形ABCD为菱形,所以AC⊥BD,
因为PO 平面PBD,BD 平面PBD,且PO∩BD=O,
所以AC⊥平面PBD,又因为AC 平面AEC,
所以平面AEC⊥平面PBD.
19.证明:(1)如图,连接EF,GH.
∵GH是△A1B1C1的中位线,∴GH∥B1C1.
∵B1E∥C1F,且B1E=C1F,∴四边形B1EFC1是平行四边形,
∴EF∥B1C1,∴EF∥GH,∴E,F,G,H四点共面.
(2)如图,延长EG,FH相交于点P.
∵P∈EG,EG 平面ABB1A1,∴P∈平面ABB1A1.
∵P∈FH,FH 平面ACC1A1,∴P∈平面ACC1A1.
∵平面ABB1A1∩平面ACC1A1=AA1,∴P∈AA1,
∴EG,FH,AA1三线共点.
20.解析:(1)证明:在△PDC中,PD=CD=3,PC=3,PD2+DC2=PC2,则PD⊥DC.
又平面PCD⊥平面ABCD,且平面PCD∩平面ABCD=CD,PD 平面PDC,故PD⊥平面ABCD.
(2)PD=3,点E是PA的中点,E到平面ABCD的距离d=PD=.
又BD⊥CD,BD=2,CD=3,S△BCD=×2×3=3.
VB CDE=VE BCD=·S△BCD·d=×3×=.
21.解析:(1)证明:取AP中点为E,连接EM,EB,
在△PAD中,M为PD的中点,E为AP中点,∴EM∥AD,EM=AD,
在平行四边形ABCD中,N为BC的中点,∴BN∥AD,BN=AD,
∴BN∥ME,BN=ME,∴四边形BNME为平行四边形,
∴MN∥BE,MN 平面PAB,BE 平面PAB,∴MN∥平面PAB.
(2)连接AN,BD,相交于O,连接OM,
∵PB∥平面AMN,平面PBD∩平面AMN=OM,PB 平面PBD,
∴PB∥OM,===,即存在点M,M为PD上靠近P点的三等分点.
22.解析:(1)l∥CD.证明:因为EB∥CD,CD 平面PBE,EB 平面PBE,所以CD∥平面PBE.
因为CD 平面PCD,平面PBE∩平面PCD=l,所以l∥CD.
(2)当平面PDE⊥平面BCDE时,四棱锥P BCDE的体积最大.
平面PDE∩平面BCDE=DE,PE 平面PDE,PE⊥DE,
可得PE⊥平面BCDE,BC 平面BCDE,可得PE⊥BC,
作EO⊥BC交BC于点O,连接PO,EO∩PE=E,
可得BC⊥平面POE,而PO在平面PEO中,故BC⊥PO,
∠POE即为二面角P BC D的平面角,
在Rt△POE中,PE=,EO=×sin 60°=,
tan ∠POE==,
所以二面角P BC D的正切值为.
(3)由展开图可知,B关于CD的对称点为B′,DE=,BB′=,由勾股定理可得AB′=,PB=,当A、G、H、B′共线时,周长最短,
此时(PG+GH+HB+PB)min=AB′+PB=+.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
