第5章 相交线与平行线 单元同步检测试题(含答案)
文档属性
| 名称 | 第5章 相交线与平行线 单元同步检测试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 460.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 15:14:18 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第五章《相交线与平行线》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.下面四个图案中,能由如图经过平移得到的是( )
A. B. C. D.
2.如图,下列说法错误的是( )
A.∠A与∠B是同旁内角 B.∠3与∠1是同旁内角
C.∠2与∠3是内错角 D.∠1与∠2是同位角
3.已知∠1和∠2是同旁内角,∠1=50°,∠2等于( )
A.150° B.130° C.40° D.无法确定
4.经过直线外一点,有几条直线和已知直线平行( )
A.0条 B.1条 C.2条 D.3条
5.如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为( )
A.16cm B.18cm C.20cm D.22cm
6.如图,如果把△ABC的顶点A先向下平移3格,再向左平移1格到达A′点,连接A′B,则线段A′B与线段AC的关系是( )
A.垂直 B.相等 C.平分 D.平分且垂直
7.如图,下列说法错误的是( )
A.∠A与∠3是同位角 B.∠4与∠B是同旁内角
C.∠A与∠C是内错角 D.∠1与∠2是同旁内角
8.平面内两两相交的3条直线,其交点个数最少为m个,最多为n个,则m+n等于( )
A.4 B.5 C.6 D.以上都不对
9.如图,已知,,,点E是线段延长线上一点,且.以下四个结论:
①;②;③平分;④.
其中结论正确的个数是( )
A.1 B.2 C.3 D.4
10.如图,直线,,分别为直线、上的点,为两平行线间的点,连接、,过点作平分交直线于点,过点作,交直线于点,若,则的度数为( )
A. B. C. D.
二、填空题(每题3分,共24分)
11.如图,直线AB∥CD,BC平分∠ABD,∠1=530;则∠2= .
12.如图,直线l1∥l2∥l3,直线AB分别交这三条平行线于点A,B,C,CD平分∠BCE交l2于点D,若∠1=110°,则∠BDC的度数是 .
13.如果两个角的两边分别平行,其中一个角是40°,则另一个角的度数是 .
13.如图,公园里长为20米宽为10米的长方形草地内修建了宽为1米的道路,则草地面积是________平方米.
14.“互补的两个角一定是同旁内角”是 命题(填“真”或“假”).
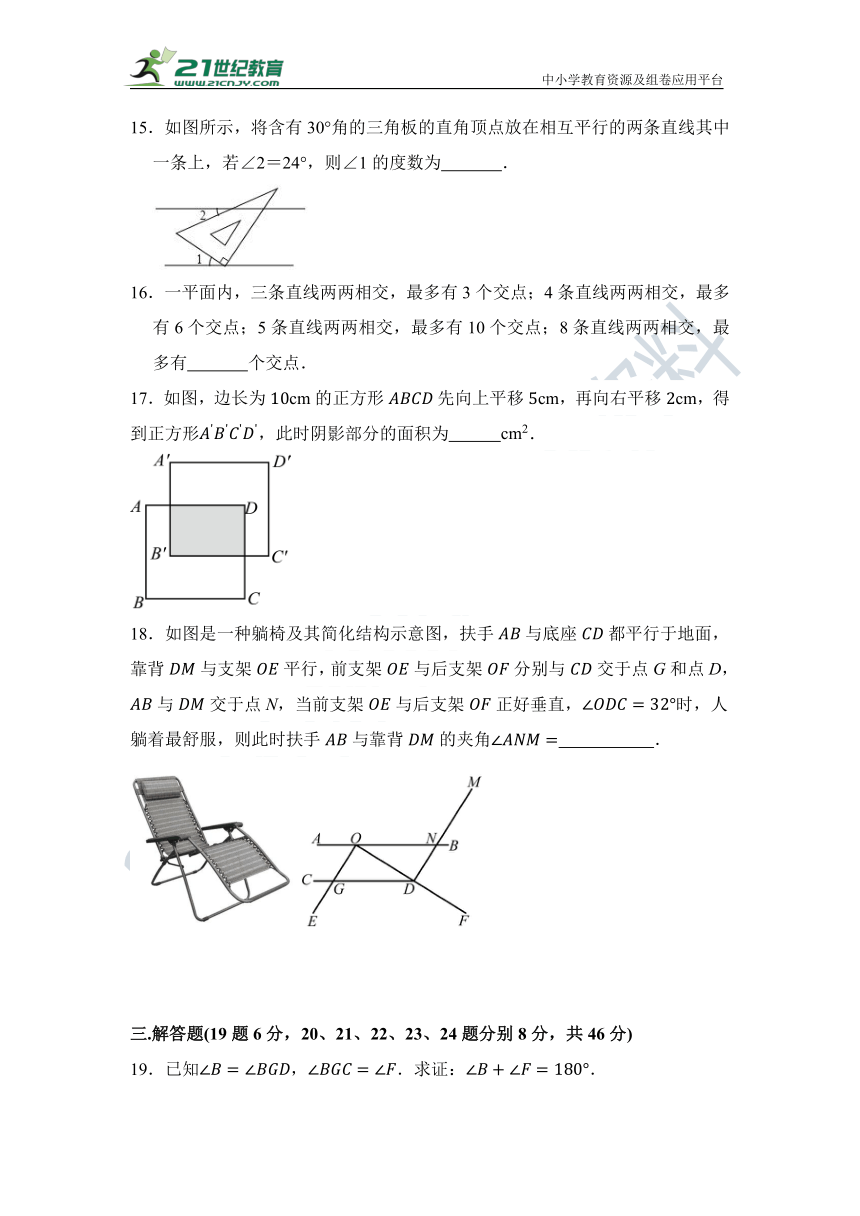
15.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠2=24°,则∠1的度数为 .
16.一平面内,三条直线两两相交,最多有3个交点;4条直线两两相交,最多有6个交点;5条直线两两相交,最多有10个交点;8条直线两两相交,最多有 个交点.
17.如图,边长为的正方形先向上平移,再向右平移,得到正方形,此时阴影部分的面积为 .
18.如图是一种躺椅及其简化结构示意图,扶手与底座都平行于地面,靠背与支架平行,前支架与后支架分别与交于点G和点D,与交于点N,当前支架与后支架正好垂直,时,人躺着最舒服,则此时扶手与靠背的夹角 .
三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)
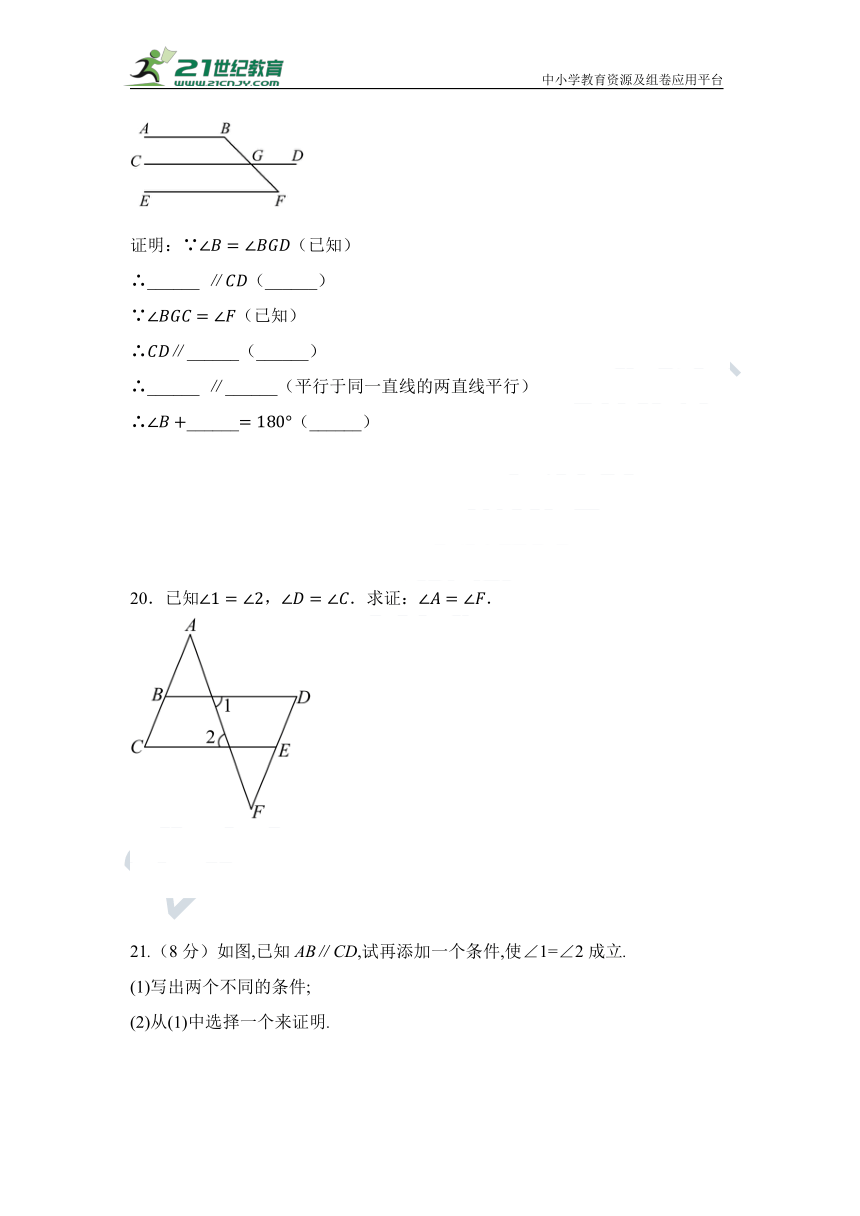
19.已知,.求证:.
证明:∵(已知)
∴______ (______)
∵(已知)
∴______(______)
∴______ ______(平行于同一直线的两直线平行)
∴______(______)
20.已知,.求证:.
21.(8分)如图,已知AB∥CD,试再添加一个条件,使∠1=∠2成立.
(1)写出两个不同的条件;
(2)从(1)中选择一个来证明.
22.(8分)如图,已知∠1+∠2=180°,∠3=∠B.
(1)试判断DE与BC的位置关系,并说明理由.
(2)若DE平分∠ADC,∠2=3∠B,求∠1的度数.
23.已知:如图,
(1)求证:;
(2)若平分平分,且,求的度数.
24.【课题学行线的“等角转化”.
如图,已知点是外一点,连接,求的度数.
解:过点作,
, ,
又.
.
【问题解决】(1)阅读并补全上述推理过程.
【解题反思】从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将,,“凑”在一起,得出角之间的关系,使问题得以解决.
【方法运用】(2)如图所示,已知,、交于点,,在图的情况下求的度数.
(3)如图,若,点在,外部,请直接写出,,之间的关系.
参考答案
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 B D B B C D A A A C
二、填空题:
11.解:∵直线AB∥CD,∠1=53°,
∴∠ABC=∠1=53°,
又∵BC平分∠ABD,
∴∠ABD=3∠ABC=∠1=106°,
∵AB∥CD,
∴∠2=∠ABD=106°,
故答案为:106°.
12.解:∵l1∥l2∥l7,
∴∠ACE+∠1=180°,
∴∠ACE=180°﹣110°=70°,
又∵CD平分∠BCE,
∴∠DCE=∠ACE=35°,
∴∠BDC=∠DCE=35°,
故答案为:35°.
13.解:
如图1,∵AB∥EF,
∴∠3=∠6,
∵BC∥DE,
∴∠3=∠1,
∴∠4=∠2.
如图2,∵AB∥EF,
∴∠3+∠2=180°,
∵BC∥DE,
∴∠3=∠7,
∴∠1+∠2=180°
∴如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
其中一个角为40°,
若两角相等,则另一个角的度数为40°;
若两角互补,则另一个角的度数为180°﹣40°=140°.
故答案为:40°或140°.
14.解:如图,∠1=∠2=90°,
∵∠1+∠2=180°,
∴∠1与∠2互补,但它们是一对内错角,不是同旁内角,
∴“互补的两个角一定是同旁内角”是假命题,
故答案为:假.
15.解:如图,延长AB交CF于E,
∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
∵GH∥EF,
∴∠AEC=∠2=24°,
∴∠1=∠ABC﹣∠AEC=36°.
故答案为:36°.
16.解:∵由已知总结出在同一平面内,n条直线两两相交,则最多有个交点,
∴8条直线两两相交,交点的个数最多为=28.
故答案为:28.
17.解:如图,
由平移得:,,,
∴,,
即阴影部分是长为,宽为的长方形,
∴阴影部分的面积为 ,
故答案为:40.
18.解:∵,,
∴.
∵,
∴,
∴.
∵,
故答案为:.
三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)
19.证明:(已知)
(内错角相等,两直线平行)
(已知)
(同位角相等,两直线平行)
(平行于同一直线的两直线平行)
(两直线平行,同旁内角互补).
20.∵,
∴,
∴,
∵,
∴,
∴,
∴.
21.解:此题答案不唯一,合理即可.
(1)添加∠FCB=∠CBE或CF∥BE.
(2)已知AB∥CD,CF∥BE.求证:∠1=∠2.
证明:∵AB∥CD,∴∠DCB=∠ABC.
∵CF∥BE,∴∠FCB=∠CBE,
∴∠DCB-∠FCB=∠ABC-∠CBE,即∠1=∠2.
22.解:(1)DE∥BC,理由如下:
∵∠1+∠4=180°,∠1+∠2=180°,
∴∠2=∠4,
∴AB∥EF,
∴∠3=∠5,
∵∠3=∠B,
∴∠5=∠B,
∴DE∥BC,
(2)∵DE平分∠ADC,
∴∠5=∠6,
∵DE∥BC,
∴∠5=∠B,
∵∠2=3∠B,
∴∠2+∠5+∠6=3∠B+∠B+∠B=180°,
∴∠B=36°,
∴∠2=108°,
∵∠1+∠2=180°,
∴∠1=72°.
23.(1)解:∵,
∴,
又∵,
∴,
∴;
(2)解:∵,
,
∵平分,
∴,
又∵平分,
∴.
24.解:(1)过点作,
,,
又,
,
故答案为:;;;
(2)过点作,
,
,
,
,
,
,
,
,
;
(3),
理由:过点作,
,
,
∴,
,
,
.
第五章《相交线与平行线》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.下面四个图案中,能由如图经过平移得到的是( )
A. B. C. D.
2.如图,下列说法错误的是( )
A.∠A与∠B是同旁内角 B.∠3与∠1是同旁内角
C.∠2与∠3是内错角 D.∠1与∠2是同位角
3.已知∠1和∠2是同旁内角,∠1=50°,∠2等于( )
A.150° B.130° C.40° D.无法确定
4.经过直线外一点,有几条直线和已知直线平行( )
A.0条 B.1条 C.2条 D.3条
5.如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为( )
A.16cm B.18cm C.20cm D.22cm
6.如图,如果把△ABC的顶点A先向下平移3格,再向左平移1格到达A′点,连接A′B,则线段A′B与线段AC的关系是( )
A.垂直 B.相等 C.平分 D.平分且垂直
7.如图,下列说法错误的是( )
A.∠A与∠3是同位角 B.∠4与∠B是同旁内角
C.∠A与∠C是内错角 D.∠1与∠2是同旁内角
8.平面内两两相交的3条直线,其交点个数最少为m个,最多为n个,则m+n等于( )
A.4 B.5 C.6 D.以上都不对
9.如图,已知,,,点E是线段延长线上一点,且.以下四个结论:
①;②;③平分;④.
其中结论正确的个数是( )
A.1 B.2 C.3 D.4
10.如图,直线,,分别为直线、上的点,为两平行线间的点,连接、,过点作平分交直线于点,过点作,交直线于点,若,则的度数为( )
A. B. C. D.
二、填空题(每题3分,共24分)
11.如图,直线AB∥CD,BC平分∠ABD,∠1=530;则∠2= .
12.如图,直线l1∥l2∥l3,直线AB分别交这三条平行线于点A,B,C,CD平分∠BCE交l2于点D,若∠1=110°,则∠BDC的度数是 .
13.如果两个角的两边分别平行,其中一个角是40°,则另一个角的度数是 .
13.如图,公园里长为20米宽为10米的长方形草地内修建了宽为1米的道路,则草地面积是________平方米.
14.“互补的两个角一定是同旁内角”是 命题(填“真”或“假”).
15.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠2=24°,则∠1的度数为 .
16.一平面内,三条直线两两相交,最多有3个交点;4条直线两两相交,最多有6个交点;5条直线两两相交,最多有10个交点;8条直线两两相交,最多有 个交点.
17.如图,边长为的正方形先向上平移,再向右平移,得到正方形,此时阴影部分的面积为 .
18.如图是一种躺椅及其简化结构示意图,扶手与底座都平行于地面,靠背与支架平行,前支架与后支架分别与交于点G和点D,与交于点N,当前支架与后支架正好垂直,时,人躺着最舒服,则此时扶手与靠背的夹角 .
三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)
19.已知,.求证:.
证明:∵(已知)
∴______ (______)
∵(已知)
∴______(______)
∴______ ______(平行于同一直线的两直线平行)
∴______(______)
20.已知,.求证:.
21.(8分)如图,已知AB∥CD,试再添加一个条件,使∠1=∠2成立.
(1)写出两个不同的条件;
(2)从(1)中选择一个来证明.
22.(8分)如图,已知∠1+∠2=180°,∠3=∠B.
(1)试判断DE与BC的位置关系,并说明理由.
(2)若DE平分∠ADC,∠2=3∠B,求∠1的度数.
23.已知:如图,
(1)求证:;
(2)若平分平分,且,求的度数.
24.【课题学行线的“等角转化”.
如图,已知点是外一点,连接,求的度数.
解:过点作,
, ,
又.
.
【问题解决】(1)阅读并补全上述推理过程.
【解题反思】从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将,,“凑”在一起,得出角之间的关系,使问题得以解决.
【方法运用】(2)如图所示,已知,、交于点,,在图的情况下求的度数.
(3)如图,若,点在,外部,请直接写出,,之间的关系.
参考答案
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 B D B B C D A A A C
二、填空题:
11.解:∵直线AB∥CD,∠1=53°,
∴∠ABC=∠1=53°,
又∵BC平分∠ABD,
∴∠ABD=3∠ABC=∠1=106°,
∵AB∥CD,
∴∠2=∠ABD=106°,
故答案为:106°.
12.解:∵l1∥l2∥l7,
∴∠ACE+∠1=180°,
∴∠ACE=180°﹣110°=70°,
又∵CD平分∠BCE,
∴∠DCE=∠ACE=35°,
∴∠BDC=∠DCE=35°,
故答案为:35°.
13.解:
如图1,∵AB∥EF,
∴∠3=∠6,
∵BC∥DE,
∴∠3=∠1,
∴∠4=∠2.
如图2,∵AB∥EF,
∴∠3+∠2=180°,
∵BC∥DE,
∴∠3=∠7,
∴∠1+∠2=180°
∴如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
其中一个角为40°,
若两角相等,则另一个角的度数为40°;
若两角互补,则另一个角的度数为180°﹣40°=140°.
故答案为:40°或140°.
14.解:如图,∠1=∠2=90°,
∵∠1+∠2=180°,
∴∠1与∠2互补,但它们是一对内错角,不是同旁内角,
∴“互补的两个角一定是同旁内角”是假命题,
故答案为:假.
15.解:如图,延长AB交CF于E,
∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
∵GH∥EF,
∴∠AEC=∠2=24°,
∴∠1=∠ABC﹣∠AEC=36°.
故答案为:36°.
16.解:∵由已知总结出在同一平面内,n条直线两两相交,则最多有个交点,
∴8条直线两两相交,交点的个数最多为=28.
故答案为:28.
17.解:如图,
由平移得:,,,
∴,,
即阴影部分是长为,宽为的长方形,
∴阴影部分的面积为 ,
故答案为:40.
18.解:∵,,
∴.
∵,
∴,
∴.
∵,
故答案为:.
三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)
19.证明:(已知)
(内错角相等,两直线平行)
(已知)
(同位角相等,两直线平行)
(平行于同一直线的两直线平行)
(两直线平行,同旁内角互补).
20.∵,
∴,
∴,
∵,
∴,
∴,
∴.
21.解:此题答案不唯一,合理即可.
(1)添加∠FCB=∠CBE或CF∥BE.
(2)已知AB∥CD,CF∥BE.求证:∠1=∠2.
证明:∵AB∥CD,∴∠DCB=∠ABC.
∵CF∥BE,∴∠FCB=∠CBE,
∴∠DCB-∠FCB=∠ABC-∠CBE,即∠1=∠2.
22.解:(1)DE∥BC,理由如下:
∵∠1+∠4=180°,∠1+∠2=180°,
∴∠2=∠4,
∴AB∥EF,
∴∠3=∠5,
∵∠3=∠B,
∴∠5=∠B,
∴DE∥BC,
(2)∵DE平分∠ADC,
∴∠5=∠6,
∵DE∥BC,
∴∠5=∠B,
∵∠2=3∠B,
∴∠2+∠5+∠6=3∠B+∠B+∠B=180°,
∴∠B=36°,
∴∠2=108°,
∵∠1+∠2=180°,
∴∠1=72°.
23.(1)解:∵,
∴,
又∵,
∴,
∴;
(2)解:∵,
,
∵平分,
∴,
又∵平分,
∴.
24.解:(1)过点作,
,,
又,
,
故答案为:;;;
(2)过点作,
,
,
,
,
,
,
,
,
;
(3),
理由:过点作,
,
,
∴,
,
,
.
