第5章 相交线与平行线单元同步检测试题(含答案)
文档属性
| 名称 | 第5章 相交线与平行线单元同步检测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 394.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 20:57:58 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第五章《相交线与平行线》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.下列运动属于平移的是( )
A.荡秋千 B.转动中的电风扇叶片
C.地球绕着太阳转 D.急刹车时,汽车在地面上的滑动
2.下列图形中,∠1与∠2不是同位角的是( )
A. B. C. D.
3.如图,直线AB,CD相交于点O,EO⊥CD于点O,若∠1=55°,则∠2的度数为( )
A.25° B.35° C.45° D.55°
4.如图,将△ABC沿射线AB平移到△DEF的位置,则以下结论不正确的是( )
A.∠C=∠F B.BC∥EF C.AD=BE D.AC=DB
5.如图,已知a,b,c,d四条直线,则∠α度数:( )
A.76° B.77° C.76°或77° D.不能确定
6.已知在同一平面内有三条不同的直线a,b,c,下列说法错误的是( )
A.如果a∥b,a⊥c,那么b⊥c B.如果b∥a,c∥a,那么b∥c
C.如果b⊥a,c⊥a,那么b⊥c D.如果b⊥a,c⊥a,那么b∥c
7.如图,下列说法错误的是( )
A.∠A与∠3是同位角 B.∠4与∠B是同旁内角
C.∠A与∠C是内错角 D.∠1与∠2是同旁内角
8.如图,,要使,则的度数是( )
A. B. C. D.
9.如图,,直线分别交,于点,,平分,,则的度数为( )
A. B. C. D.
10.如图,已知,,,点E是线段延长线上一点,且.以下四个结论:
①;②;③平分;④.
其中结论正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(每题3分,共24分)
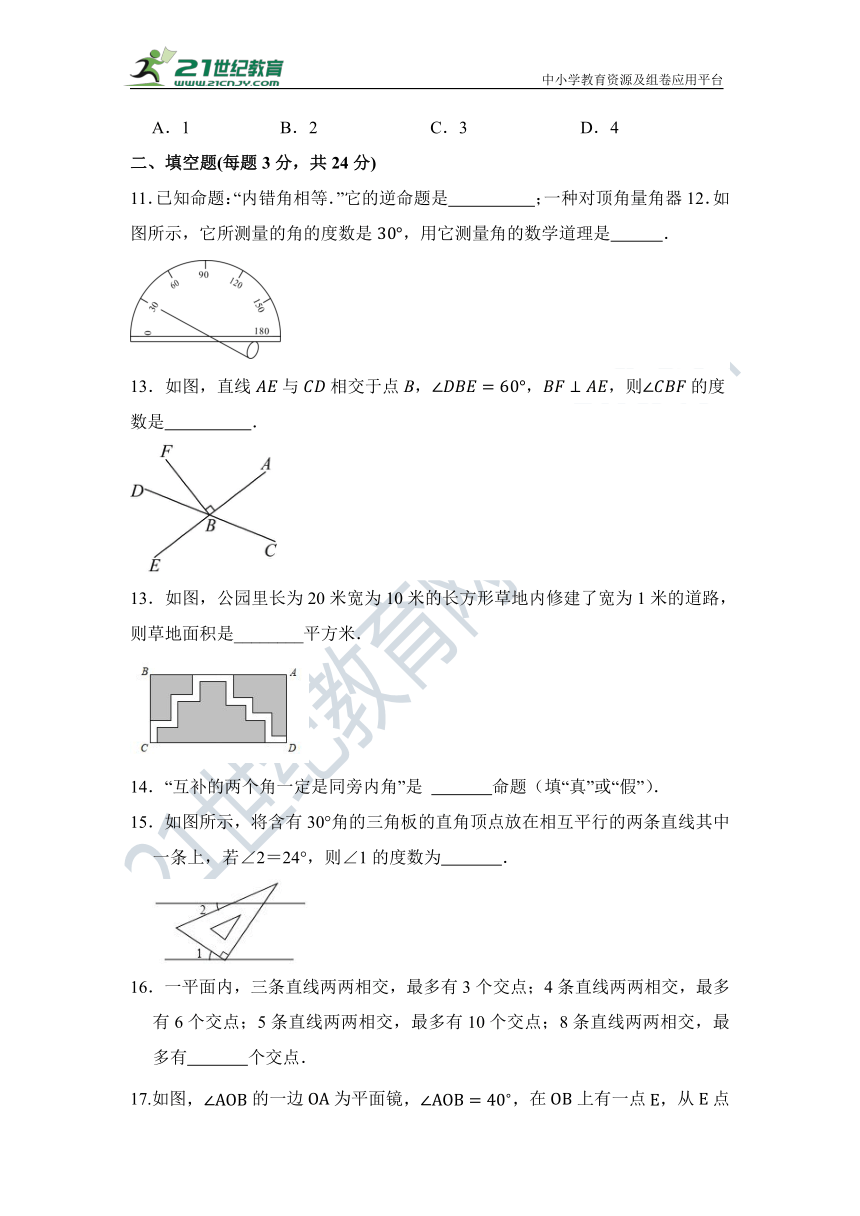
11.已知命题:“内错角相等.”它的逆命题是 ;一种对顶角量角器12.如图所示,它所测量的角的度数是,用它测量角的数学道理是 .
13.如图,直线与相交于点B,,,则的度数是 .
13.如图,公园里长为20米宽为10米的长方形草地内修建了宽为1米的道路,则草地面积是________平方米.
14.“互补的两个角一定是同旁内角”是 命题(填“真”或“假”).
15.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠2=24°,则∠1的度数为 .
16.一平面内,三条直线两两相交,最多有3个交点;4条直线两两相交,最多有6个交点;5条直线两两相交,最多有10个交点;8条直线两两相交,最多有 个交点.
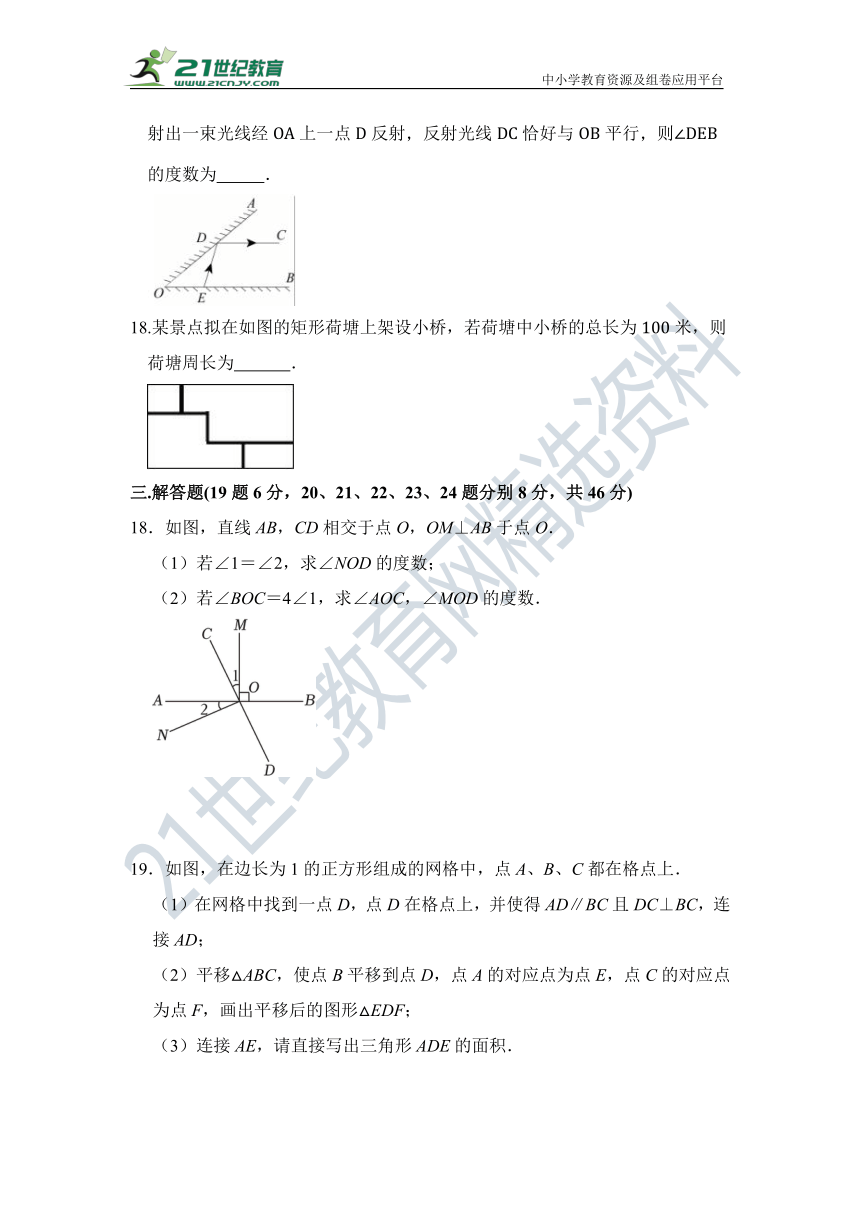
17.如图的一边为平面镜在上有一点从点射出一束光线经上一点反射反射光线恰好与平行则的度数为 .
18.某景点拟在如图的矩形荷塘上架设小桥,若荷塘中小桥的总长为米,则荷塘周长为 .
三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)
18.如图,直线AB,CD相交于点O,OM⊥AB于点O.
(1)若∠1=∠2,求∠NOD的度数;
(2)若∠BOC=4∠1,求∠AOC,∠MOD的度数.
19.如图,在边长为1的正方形组成的网格中,点A、B、C都在格点上.
(1)在网格中找到一点D,点D在格点上,并使得AD∥BC且DC⊥BC,连接AD;
(2)平移△ABC,使点B平移到点D,点A的对应点为点E,点C的对应点为点F,画出平移后的图形△EDF;
(3)连接AE,请直接写出三角形ADE的面积.
20. 如图、点 、 均在直线 上,点 在直线 上,连接 , , 平分 交 于 ,连接 , , .求证: .
21.(8分)如图,已知AB∥CD,试再添加一个条件,使∠1=∠2成立.
(1)写出两个不同的条件;
(2)从(1)中选择一个来证明.
22.(8分)如图,已知∠1+∠2=180°,∠3=∠B.
(1)试判断DE与BC的位置关系,并说明理由.
(2)若DE平分∠ADC,∠2=3∠B,求∠1的度数.
23.如图,直线AB,CD被EF所截,∠1+∠2=1800,EM,FN分别平分∠BEF和∠CFE.
(1)判定EM与FN之间的位置关系,并证明你的结论;
(2)①由(1)的结论我们可以得到一个命题:如果两条平行线被第三条直线所截,那么一组内错角的角平分线互相 ;
②由此可以探究并得到:如果两条平行线被第三条直线所截,那么一组同旁内角的角平分线互相 ,请说明理由.
24.如图,∠B=∠ADC=90°,且∠MAD=∠BCD.
(1)当AE和CF分别为∠BAD与∠BCD平分线时(如图1),则∠BAD+∠BCM= ,判断AE和CF的位置关系是 ;
(2)延长MC,当AE和CF分别为∠MAD和∠BCH的平分线时(如图2),判断AE和CF的位置关系;
(3)当AE和CF分别为∠BAD和∠BCE的平分线时(如图3),请探索AE和CF的位置关系,并说明理由.
参考答案
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 D B B D B C A D C C
二、填空题:
11.对顶角相等
12.如果两个角相等,那么这两个角是内错角
13.
14.解:如图,∠1=∠2=90°,
∵∠1+∠2=180°,
∴∠1与∠2互补,但它们是一对内错角,不是同旁内角,
∴“互补的两个角一定是同旁内角”是假命题,
故答案为:假.
15.解:如图,延长AB交CF于E,
∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
∵GH∥EF,
∴∠AEC=∠2=24°,
∴∠1=∠ABC﹣∠AEC=36°.
故答案为:36°.
16.解:∵由已知总结出在同一平面内,n条直线两两相交,则最多有个交点,
∴8条直线两两相交,交点的个数最多为=28.
故答案为:28.
17.
18.
三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)
19.解:(1)如图,点D即为所求.
(2)如图,△EDF即为所求.
(3)三角形ADE的面积为=3.
20.证明:∵AF平分∠BAD,
∴∠BAM=∠DAM,
∵∠DAM=∠DMA,
∴∠BAM=∠DMA,
∴AB∥CD,
∴∠B=∠DCF,
∵∠B=∠D,
∴∠D=∠DCF,
∴AD∥BC,
∴∠E=∠EFB.
21.解:此题答案不唯一,合理即可.
(1)添加∠FCB=∠CBE或CF∥BE.
(2)已知AB∥CD,CF∥BE.求证:∠1=∠2.
证明:∵AB∥CD,∴∠DCB=∠ABC.
∵CF∥BE,∴∠FCB=∠CBE,
∴∠DCB-∠FCB=∠ABC-∠CBE,即∠1=∠2.
22.解:(1)DE∥BC,理由如下:
∵∠1+∠4=180°,∠1+∠2=180°,
∴∠2=∠4,
∴AB∥EF,
∴∠3=∠5,
∵∠3=∠B,
∴∠5=∠B,
∴DE∥BC,
(2)∵DE平分∠ADC,
∴∠5=∠6,
∵DE∥BC,
∴∠5=∠B,
∵∠2=3∠B,
∴∠2+∠5+∠6=3∠B+∠B+∠B=180°,
∴∠B=36°,
∴∠2=108°,
∵∠1+∠2=180°,
∴∠1=72°.
23.解:(1)EM∥FN.
证明:∵∠1+∠2=180°,∠EFD+∠7=180°,
∴∠1=∠EFD,
∴AB∥CD,
∴∠BEF=∠CFE.
∵EM,FN分别平分∠BEF和∠CFE,
∴∠3=∠6,
∴EM∥FN.
(2)由(1)可知EM∥FN,
∴可得出命题:如果两条直线平行,那么内错角的角平分线互相平行.
故答案为:平行.
(3)由“两直线平行,同旁内角互补”可得出:
如果两条直线平行,那么同旁内角的角平分线互相垂直.
如图:AB∥CD,EG平分∠BEF,
∵AB∥CD,
∴∠BEF+∠EFD=180°,
∴∠FEG=∠BEF∠EFD,
∴∠FEG+∠EFG=(∠BEF+∠EFD)=90°,
∴∠EGF=90°,
∴EG⊥FG.
故答案为:垂直.
24.解:(1)∵∠BAD+∠BCD=∠1+∠2+∠3+∠4=360°﹣(∠B+∠D),
∵∠B=∠D=90°.∠1=∠5,
∴∠BAD+∠BCD=2(∠2+∠7)=360°﹣180°=180°,
则∠2+∠4=90°,
又∵∠B=90°,
∴3+∠5=90°,
∴∠4=∠3.
∴AE∥CF.
故答案为:180°,AE∥CF;
(2)AE∥CF.理由如下:
作DP∥AE,如图2,
∵四边形ABCD中,∠B=∠ADC=90°,
∴∠BAD+∠BCD=180°,
∴∠MAD+∠BCH=180°,
∵AE,CF都为角平分线,
∴∠1=∠GAD∠BCH,
∴∠1+∠4=90°,
∵PD∥AE,
∴∠6=∠2,
而∠2+∠2=90°,
∴∠1+∠3=90°,
∴∠3=∠4,
∴PD∥CF,
∴AE∥CF;
(3)AE⊥CF.理由如下:
如图3,
∵四边形ABCD中,∠B=∠D=90°,
∴∠BAD+∠BCD=180°,
∴∠BAD=∠BCE,
∵AE,CF都为角平分线,
∴∠7=∠BAD∠BCE,
∴∠1=∠8,
而∠3=∠4,
∴∠5=∠B=90°,
∴AE⊥CF.
第五章《相交线与平行线》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.下列运动属于平移的是( )
A.荡秋千 B.转动中的电风扇叶片
C.地球绕着太阳转 D.急刹车时,汽车在地面上的滑动
2.下列图形中,∠1与∠2不是同位角的是( )
A. B. C. D.
3.如图,直线AB,CD相交于点O,EO⊥CD于点O,若∠1=55°,则∠2的度数为( )
A.25° B.35° C.45° D.55°
4.如图,将△ABC沿射线AB平移到△DEF的位置,则以下结论不正确的是( )
A.∠C=∠F B.BC∥EF C.AD=BE D.AC=DB
5.如图,已知a,b,c,d四条直线,则∠α度数:( )
A.76° B.77° C.76°或77° D.不能确定
6.已知在同一平面内有三条不同的直线a,b,c,下列说法错误的是( )
A.如果a∥b,a⊥c,那么b⊥c B.如果b∥a,c∥a,那么b∥c
C.如果b⊥a,c⊥a,那么b⊥c D.如果b⊥a,c⊥a,那么b∥c
7.如图,下列说法错误的是( )
A.∠A与∠3是同位角 B.∠4与∠B是同旁内角
C.∠A与∠C是内错角 D.∠1与∠2是同旁内角
8.如图,,要使,则的度数是( )
A. B. C. D.
9.如图,,直线分别交,于点,,平分,,则的度数为( )
A. B. C. D.
10.如图,已知,,,点E是线段延长线上一点,且.以下四个结论:
①;②;③平分;④.
其中结论正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(每题3分,共24分)
11.已知命题:“内错角相等.”它的逆命题是 ;一种对顶角量角器12.如图所示,它所测量的角的度数是,用它测量角的数学道理是 .
13.如图,直线与相交于点B,,,则的度数是 .
13.如图,公园里长为20米宽为10米的长方形草地内修建了宽为1米的道路,则草地面积是________平方米.
14.“互补的两个角一定是同旁内角”是 命题(填“真”或“假”).
15.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠2=24°,则∠1的度数为 .
16.一平面内,三条直线两两相交,最多有3个交点;4条直线两两相交,最多有6个交点;5条直线两两相交,最多有10个交点;8条直线两两相交,最多有 个交点.
17.如图的一边为平面镜在上有一点从点射出一束光线经上一点反射反射光线恰好与平行则的度数为 .
18.某景点拟在如图的矩形荷塘上架设小桥,若荷塘中小桥的总长为米,则荷塘周长为 .
三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)
18.如图,直线AB,CD相交于点O,OM⊥AB于点O.
(1)若∠1=∠2,求∠NOD的度数;
(2)若∠BOC=4∠1,求∠AOC,∠MOD的度数.
19.如图,在边长为1的正方形组成的网格中,点A、B、C都在格点上.
(1)在网格中找到一点D,点D在格点上,并使得AD∥BC且DC⊥BC,连接AD;
(2)平移△ABC,使点B平移到点D,点A的对应点为点E,点C的对应点为点F,画出平移后的图形△EDF;
(3)连接AE,请直接写出三角形ADE的面积.
20. 如图、点 、 均在直线 上,点 在直线 上,连接 , , 平分 交 于 ,连接 , , .求证: .
21.(8分)如图,已知AB∥CD,试再添加一个条件,使∠1=∠2成立.
(1)写出两个不同的条件;
(2)从(1)中选择一个来证明.
22.(8分)如图,已知∠1+∠2=180°,∠3=∠B.
(1)试判断DE与BC的位置关系,并说明理由.
(2)若DE平分∠ADC,∠2=3∠B,求∠1的度数.
23.如图,直线AB,CD被EF所截,∠1+∠2=1800,EM,FN分别平分∠BEF和∠CFE.
(1)判定EM与FN之间的位置关系,并证明你的结论;
(2)①由(1)的结论我们可以得到一个命题:如果两条平行线被第三条直线所截,那么一组内错角的角平分线互相 ;
②由此可以探究并得到:如果两条平行线被第三条直线所截,那么一组同旁内角的角平分线互相 ,请说明理由.
24.如图,∠B=∠ADC=90°,且∠MAD=∠BCD.
(1)当AE和CF分别为∠BAD与∠BCD平分线时(如图1),则∠BAD+∠BCM= ,判断AE和CF的位置关系是 ;
(2)延长MC,当AE和CF分别为∠MAD和∠BCH的平分线时(如图2),判断AE和CF的位置关系;
(3)当AE和CF分别为∠BAD和∠BCE的平分线时(如图3),请探索AE和CF的位置关系,并说明理由.
参考答案
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 D B B D B C A D C C
二、填空题:
11.对顶角相等
12.如果两个角相等,那么这两个角是内错角
13.
14.解:如图,∠1=∠2=90°,
∵∠1+∠2=180°,
∴∠1与∠2互补,但它们是一对内错角,不是同旁内角,
∴“互补的两个角一定是同旁内角”是假命题,
故答案为:假.
15.解:如图,延长AB交CF于E,
∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
∵GH∥EF,
∴∠AEC=∠2=24°,
∴∠1=∠ABC﹣∠AEC=36°.
故答案为:36°.
16.解:∵由已知总结出在同一平面内,n条直线两两相交,则最多有个交点,
∴8条直线两两相交,交点的个数最多为=28.
故答案为:28.
17.
18.
三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)
19.解:(1)如图,点D即为所求.
(2)如图,△EDF即为所求.
(3)三角形ADE的面积为=3.
20.证明:∵AF平分∠BAD,
∴∠BAM=∠DAM,
∵∠DAM=∠DMA,
∴∠BAM=∠DMA,
∴AB∥CD,
∴∠B=∠DCF,
∵∠B=∠D,
∴∠D=∠DCF,
∴AD∥BC,
∴∠E=∠EFB.
21.解:此题答案不唯一,合理即可.
(1)添加∠FCB=∠CBE或CF∥BE.
(2)已知AB∥CD,CF∥BE.求证:∠1=∠2.
证明:∵AB∥CD,∴∠DCB=∠ABC.
∵CF∥BE,∴∠FCB=∠CBE,
∴∠DCB-∠FCB=∠ABC-∠CBE,即∠1=∠2.
22.解:(1)DE∥BC,理由如下:
∵∠1+∠4=180°,∠1+∠2=180°,
∴∠2=∠4,
∴AB∥EF,
∴∠3=∠5,
∵∠3=∠B,
∴∠5=∠B,
∴DE∥BC,
(2)∵DE平分∠ADC,
∴∠5=∠6,
∵DE∥BC,
∴∠5=∠B,
∵∠2=3∠B,
∴∠2+∠5+∠6=3∠B+∠B+∠B=180°,
∴∠B=36°,
∴∠2=108°,
∵∠1+∠2=180°,
∴∠1=72°.
23.解:(1)EM∥FN.
证明:∵∠1+∠2=180°,∠EFD+∠7=180°,
∴∠1=∠EFD,
∴AB∥CD,
∴∠BEF=∠CFE.
∵EM,FN分别平分∠BEF和∠CFE,
∴∠3=∠6,
∴EM∥FN.
(2)由(1)可知EM∥FN,
∴可得出命题:如果两条直线平行,那么内错角的角平分线互相平行.
故答案为:平行.
(3)由“两直线平行,同旁内角互补”可得出:
如果两条直线平行,那么同旁内角的角平分线互相垂直.
如图:AB∥CD,EG平分∠BEF,
∵AB∥CD,
∴∠BEF+∠EFD=180°,
∴∠FEG=∠BEF∠EFD,
∴∠FEG+∠EFG=(∠BEF+∠EFD)=90°,
∴∠EGF=90°,
∴EG⊥FG.
故答案为:垂直.
24.解:(1)∵∠BAD+∠BCD=∠1+∠2+∠3+∠4=360°﹣(∠B+∠D),
∵∠B=∠D=90°.∠1=∠5,
∴∠BAD+∠BCD=2(∠2+∠7)=360°﹣180°=180°,
则∠2+∠4=90°,
又∵∠B=90°,
∴3+∠5=90°,
∴∠4=∠3.
∴AE∥CF.
故答案为:180°,AE∥CF;
(2)AE∥CF.理由如下:
作DP∥AE,如图2,
∵四边形ABCD中,∠B=∠ADC=90°,
∴∠BAD+∠BCD=180°,
∴∠MAD+∠BCH=180°,
∵AE,CF都为角平分线,
∴∠1=∠GAD∠BCH,
∴∠1+∠4=90°,
∵PD∥AE,
∴∠6=∠2,
而∠2+∠2=90°,
∴∠1+∠3=90°,
∴∠3=∠4,
∴PD∥CF,
∴AE∥CF;
(3)AE⊥CF.理由如下:
如图3,
∵四边形ABCD中,∠B=∠D=90°,
∴∠BAD+∠BCD=180°,
∴∠BAD=∠BCE,
∵AE,CF都为角平分线,
∴∠7=∠BAD∠BCE,
∴∠1=∠8,
而∠3=∠4,
∴∠5=∠B=90°,
∴AE⊥CF.
