一元二次不等式

课件37张PPT。 一元二次不等式及其解法一元二次不等式
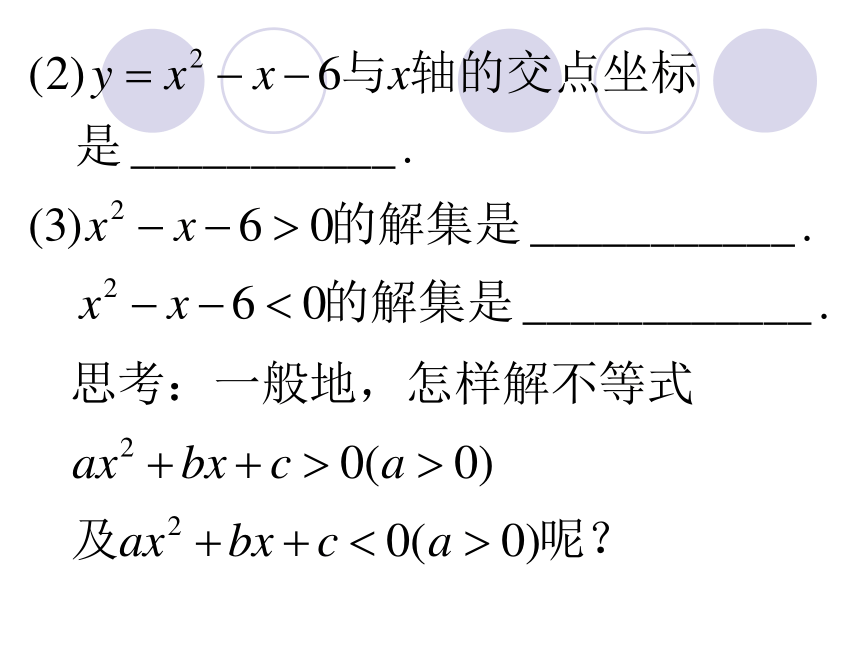
一般地，含有 未知数，且未知数的最高次数为 的不等式，叫做一元二次不等式．
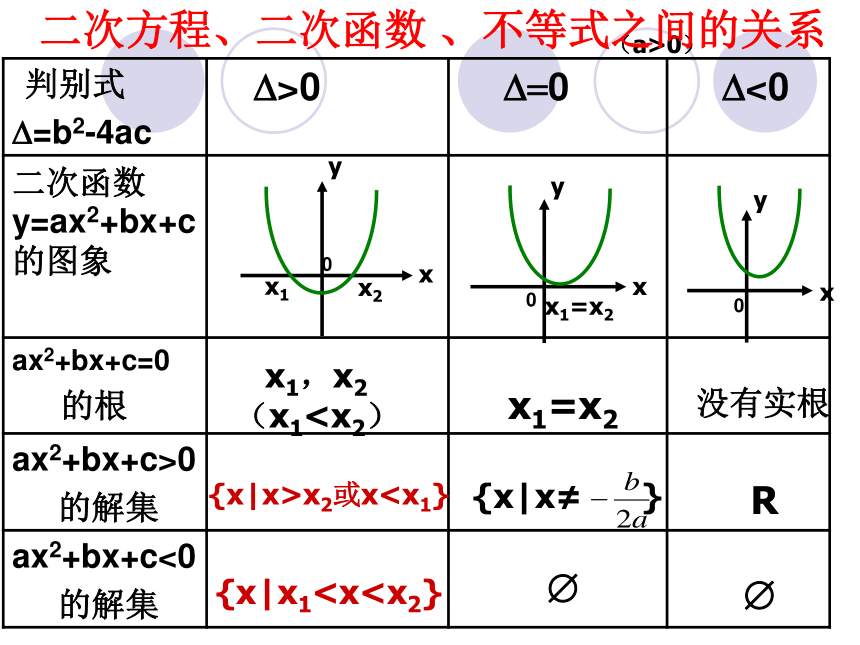
一个2（a>0） x1，x2
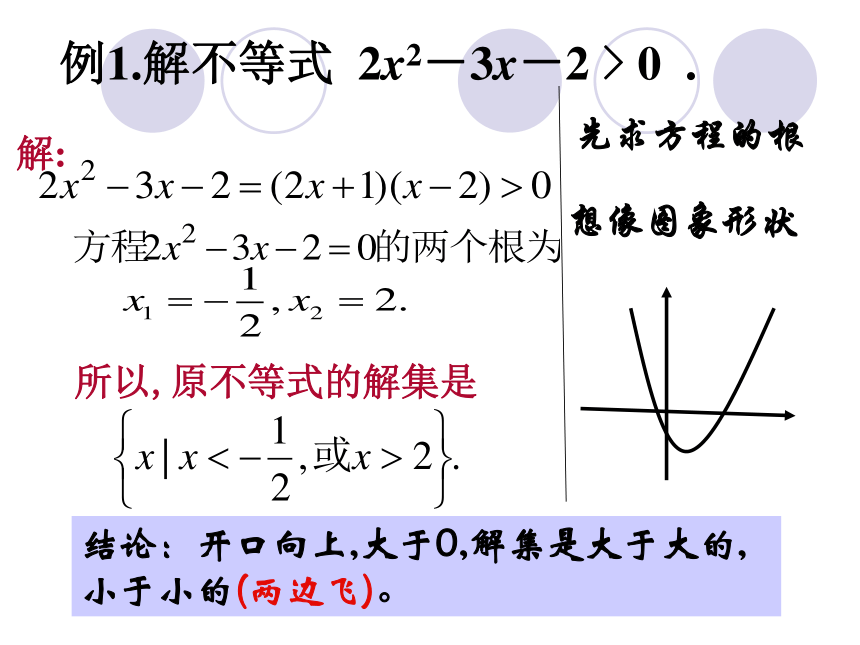
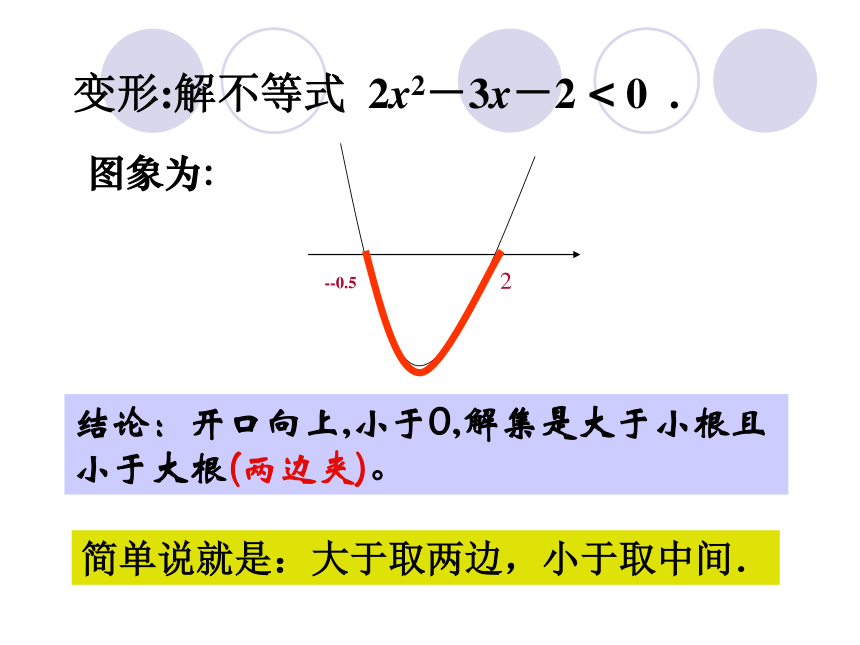
（x1x2或x 0 .解:所以,原不等式的解集是先求方程的根想像图象形状结论：开口向上,大于0,解集是大于大的,小于小的(两边飞)。变形:解不等式 2x2－3x－2 < 0 .图象为:结论：开口向上,小于0,解集是大于小根且小于大根(两边夹)。简单说就是：大于取两边，小于取中间．例2.解不等式 －3x2＋6x > 2解: ∵－3x2＋6x > 2∴3x2－6x＋2 < 0∵方程3x2－6x+2 =0的解是∴原不等式的解集是例3.解不等式 4x2－4x＋1 > 0 解:4x2－4x＋1=（2x-1）2> 0
方程4x2－4x＋1 =0的解是所以,原不等式的解集是注:4x2－4x＋1 <0解一元二次不等式的步骤：1.把二次项的系数变为正的。2、求解对应的一元二次方程的根3、求解一元二次不等式（根据一元二次方程的根及不等式的符号）（如果是负，那么在不等式两边都乘以-1，把系数变为正）（先看能否因式分解，若不能，再看△，或进行配方）练习解下列不等式：例4、一个汽车制造厂引进了一条摩托车整车装配流水线，这条流水线生产的摩托车数量x（辆）与创造的价值y（元）之间有如下的关系：若这家工厂希望在一个星期内利用这条流水线创收6000元以上，那么它在一个星期内大约应该生产多少辆摩托车？ 方法小结一元二次不等式恒成立情况：
解关于x的不等式x2＋ax－2a2＜0.[规范作答]　原不等式可化为(x＋2a)(x－a)＜0
对应的一元二次方程的根为x1＝a，x2＝－2a，3分
(1)当a＞0时，x1＞x2，
不等式的解集为{x|－2a＜x＜a}.6分
(2)当a＝0时，原不等式化为x2＜0，无解.8分
(3)当a＜0时，x1＜x2，
不等式的解集为{x|a＜x＜－2a}.10分
综上所述，原不等式的解集为：
a＞0时，{x|－2a＜x＜a}
a＝0时，?
a＜0时，{x|a＜x＜－2a}12分备选内容：分式不等式、高次不等式先将不等式两边中所有的非零项都移到不等式的左边，
并整理为下列某种形式，然后转化为为整式不等(组)，
灵活选择方法进行求解.例1、解下列不等式 若对于不等式f(x)>0，其中f(x)为x的高次多项式，用数轴标根法解不等式f(x)>0的步骤如下：1、整理 把f(x)进行因式分解，并化简成下面的形式:
(x-a1)(x-a2)·…·(x-an)>0(或<0)
这里的每一个因式中x的系数为1，彼此不等2、标根 将f(x)=0的n个不同的根a1、a2、… an标在
数轴上,把数轴分成n+1个区间 另外，将恒不为零的二次因式约去，同时保持各因式中的系数为正号，对于多重根的因式可先将偶次因式约去，单独考虑重根是否为不等式的解练习：解不等式：4、选解 下图中，在x轴上方的曲线对应的区间为
(x-a1)(x-a2)·…·(x-an)>0的解集，在轴下方的
曲线对应的区间为(x-a1)(x-a2)·…·(x-an)<0的解集5函数方程不等式方程的解不等式的解集不等式的解集y>0y>0y<0二次函数、二次方程、与二次不等式的关系关键在于快速准确捕捉图像的特征一元二次不等式可用图象法求解题型一 （1）分式不等式的解法题型二 三个“二次”间对应关系的应用 1、已知关于x的不等式 x2＋ax＋b<0的解集为{x|10的解集． 2、若二次不等式ax2＋bx＋c<0的解集为
{x|x< ，或x> }，试求关于x的不等式
cx2-bx＋a>0的解集．题型三 （2）一元高次不等式的解法2、求 的解集。3、求(x-1)2(x-2)3(x-3)(x+1)<0的解集。1、求不等式(x-1)(x-2)(x-3)>0的解集。数轴标根法步骤：1、找根；2、画轴；3、标根；4、画波浪曲线；5、看图得解。 方法总结：1、从右上向左画；
2、奇穿偶不穿。题型四 一元二次不等式恒成立问题方法小结一元二次不等式恒成立情况：(1)ax2+2a2x － 3a3 >0(a≥0);
(2)m2x2＋2mx －3<0;
(3)2x2＋ax＋2>0；题型三 解含参数的一元二次不等式(3)对于判别式大于0的情况，需对两根的大小进行讨论；
(4)最后按照一元二次不等式的解法求出解集(1)当二次项系数含有参数时，应先对二次项系数进行分类讨论；(2)当二次项系数不为零时，看能否因式分解，思路:若不能则对其判别式进行分类讨论；解：　
(1) 由题可得Δ＝a2－16①当Δ<0， 即－40， 即a>4或a<-4时，2x2＋ax＋2＝0的
两个根为 ，
若a=4，则 ，
原不等式解集为
若a=-4，则 ，
原不等式解集为
③当Δ=0， 即a=4或a=-4时，2x2＋ax＋2＝0
有两个相同的实数根。练习-12 -2解：当a>0时不合，a=0也不合，∴ 必有：题型一 恒成立问题∴ k的取值范围是[0，1] 解：显然k=0时满足，而k<0时不满足，(3)对于判别式大于0的情况，需对两根的大小进行讨论；
(4)最后按照一元二次不等式的解法求出解集(1)当二次项系数含有参数时，应先对二次项系数进行分类讨论；(2)当二次项系数不为零时，看能否因式分解，思路:若不能则对其判别式进行分类讨论；