人教版七年级数学下册第七章平面直角坐标系单元复习题(含解析)
文档属性
| 名称 | 人教版七年级数学下册第七章平面直角坐标系单元复习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 283.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 00:00:00 | ||
图片预览



文档简介
人教版七年级数学下册第七章平面直角坐标系单元复习题
一、选择题
1.如果把电影票上“5排3座”记作,那么表示( )
A.“4排4座” B.“9排4座” C.“4排9座” D.“9排9座”
2.在平面直角坐标系中,点P(,2)位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.点A(﹣1,2)到x轴的距离是( )
A.﹣1 B.1 C.﹣2 D.2
4.某气象台为了预报台风,首先需要确定台风中心的位置,则下列说法能确定台风中心位置的是( )
A.北纬 B.距气象台海里
C.北纬,东经 D.北海市附近
5.已知点Q的坐标为 ,点P的坐标为 ,若直线 轴,则点P的坐标为( )
A. B. C. D.
6.如图,小明从点O出发,先向西走400m,再向南走300m到达点M,如果点M的位置用(-4,-3)表示,那么(1,2)表示的位置是( )
A.点A B.点B C.点C D.点D
7.点P(m+3,m﹣2)在直角坐标系的x轴上,则点P的坐标为( )
A.(0,5) B.(5,0) C.(﹣5,0) D.(0,﹣5)
8.如图,关于小明家相对于学校的位置,下列描述最正确的是( )
A.在距离学校米处 B.在学校的东南方向
C.在南偏东方向米处 D.在学校北偏西方向米处
9.在平面直角坐标系中,将三角形各点的纵坐标都减去3,横坐标保持不变,所得图形与原图形相比 ( )
A.向右平移了3个单位 B.向左平移了3个单位
C.向上平移了3个单位 D.向下平移了3个单位
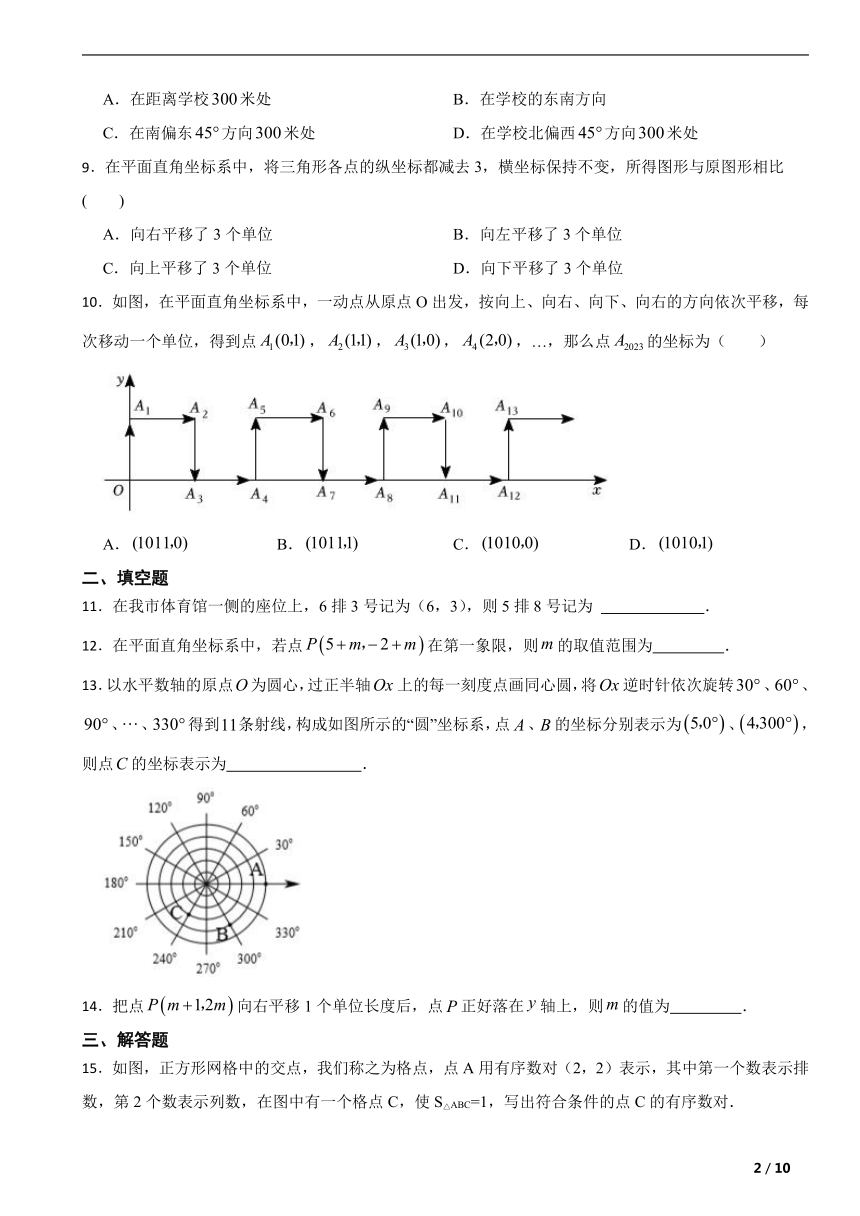
10.如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次平移,每次移动一个单位,得到点,,,,…,那么点的坐标为( )
A. B. C. D.
二、填空题
11.在我市体育馆一侧的座位上,6排3号记为(6,3),则5排8号记为 .
12.在平面直角坐标系中,若点在第一象限,则的取值范围为 .
13.以水平数轴的原点为圆心,过正半轴上的每一刻度点画同心圆,将逆时针依次旋转、、、、得到条射线,构成如图所示的“圆”坐标系,点、的坐标分别表示为、,则点的坐标表示为 .
14.把点向右平移1个单位长度后,点正好落在轴上,则的值为 .
三、解答题
15.如图,正方形网格中的交点,我们称之为格点,点A用有序数对(2,2)表示,其中第一个数表示排数,第2个数表示列数,在图中有一个格点C,使S△ABC=1,写出符合条件的点C的有序数对.
16.已知在平面直角坐标系中,点A的坐标为.
(1)若点A在轴上,求出点A的坐标;
(2)若点A到轴的距离为,求出点A的坐标.
17.如图所示,求出A,B,C,D,E,F,O点的坐标.
18.在平面直角坐标系中,点M的坐标为,点N的坐标为.若轴,求点M的坐标.
19.已知点请分别根据下列条件,求出点P的坐标.
(1)点P在x轴上;
(2)点P的纵坐标比横坐标大5;
(3)点P在过点且与y轴平行的直线上.
20.如图是某学校的平面示意图,已知旗杆的位置是(-2,3),实验室的位置是(1,4)
(1)根据所给条件在图中建立适当的平面直角坐标系;
(2)用坐标表示位置:食堂 ,图书馆 .
(3)已知办公楼的位置是(-2,1),教学楼的位置是(2,2),在图中标出办公楼和教学楼的位置;
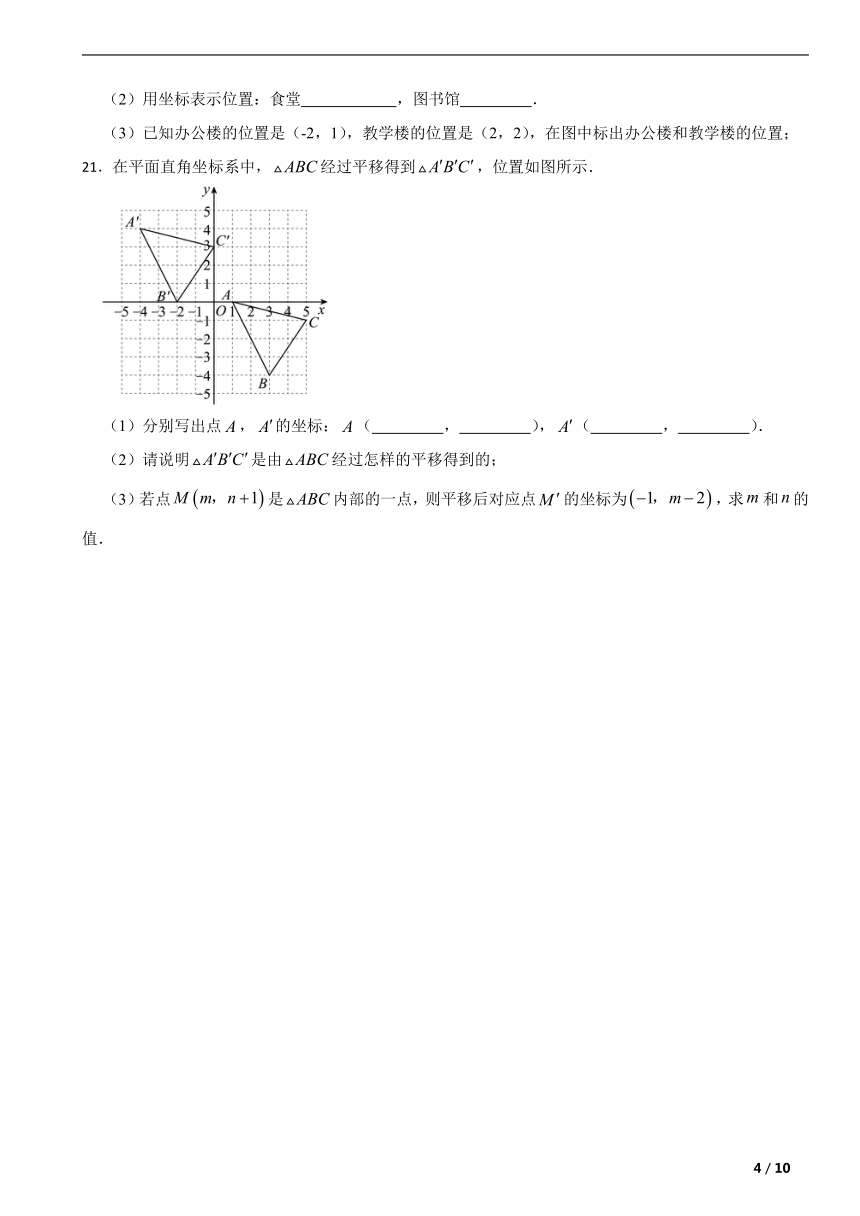
21.在平面直角坐标系中,经过平移得到,位置如图所示.
(1)分别写出点,的坐标:( , ),( , ).
(2)请说明是由经过怎样的平移得到的;
(3)若点是内部的一点,则平移后对应点的坐标为,求和的值.
答案解析部分
1.【答案】C
【解析】【解答】解:“5排3座”记作,
表示“4排9座”.
故答案为:C.
【分析】由已知有序数对知:横坐标表示排数,纵坐标表示座号,从而得解.
2.【答案】B
【解析】【解答】P(,2)位于第二象限,
故答案为:B
【分析】根据各象限内点的坐标的符号特征:第一象限(+,+)第二象限(-,+)第三象限(-,-)第四象限(+,-),据此判断即可.
3.【答案】D
【解析】【解答】解:点P(-1,2)到x轴的距离是2.
故答案为:D.
【分析】根据点到x轴的距离等于在这边的绝对值解答即可。
4.【答案】C
【解析】【解答】解:A、不能确定台风中心位置,故A不符合题意;
B、不能确定台风中心位置,故B不符合题意;
C、能确定台风中心位置,故C符合题意;
D、不能确定台风中心位置,故D不符合题意.
故答案为:C.
【分析】 根据确定一个物体的位置需要两个量,逐项进行判断,即可得出答案.
5.【答案】C
【解析】【解答】解:∵点Q的坐标为(2,-3),点P的坐标为(2a+2,a-5),直线PQ⊥y轴,
∴a-5=-3,
∴a=2,
∴2a+2=6,
∴点P的坐标为(6,-3).
故答案为:C.
【分析】根据垂直于y轴的直线所有点的纵坐标相等即可求得a的值,即可得出答案.
6.【答案】B
【解析】【解答】解:∵点M的位置用( 4, 3)表示,实际意义为从点O出发,先向西走400m,再向南走300m,也就是网格中一个小正方形边长为100m,
∴(1,2)表示的位置实际意义为先向东走100m,再向北走200m,对应的是点B,
故答案为:B.
【分析】根据有序数对的表示方法求解即可。
7.【答案】B
【解析】【解答】解:∵点P在直角坐标系的x轴上,
∴m﹣2=0,
∴m=2,
故点P的横坐标为:m+3=2+3=5,
即点P的坐标为(5,0)
故选B.
【分析】由点P在直角坐标系的x轴上得出m﹣2=0,可求出m的值,然后求出点P的坐标即可.
8.【答案】D
【解析】【解答】解:根据图形中的数据可得:小明家在学校北偏西45°方向300米处,
故答案为:D.
【分析】根据图形中的数据直接求出答案即可.
9.【答案】D
【解析】【解答】将三角形各点的纵坐标都减去3,横坐标保持不变,所得图形与原图形相比向下平移了3个单位.
故选:D.
【分析】根据平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减,可得答案.
10.【答案】A
【解析】【解答】解:由图象可知:每移动4次图象完成一个循环,每个循环结束图象向右移动2个单位,
∵2023÷4=505······3,
∴点A的坐标为(505×2+1,0),即(1011,0),
故答案为:A.
【分析】由图象可知:每移动4次图象完成一个循环,每个循环结束图象向右移动2个单位,据此解答即可.
11.【答案】(5,8)
【解析】【解答】解:∵6排3号记为(6,3),
∴5排8号记为(5,8),
故答案为:(5,8).
【分析】根据有序数对的定义求解即可。
12.【答案】
【解析】【解答】∵点在第一象限,
∴,解得,
故答案为:.
【分析】根据点坐标与象限的关系可得不等式组,再求出m的取值范围即可。
13.【答案】(3,240°)
【解析】【解答】解: ∵点、的坐标分别表示为、,
∴圆所在的层数表示横坐标,射线对应的度数表示纵坐标,
∴C(3,240°);
故答案为:(3,240°).
【分析】观察图形及点A、B的坐标,可知圆所在的层数表示横坐标,射线对应的度数表示纵坐标,据此即可求解.
14.【答案】
【解析】【解答】将点P向右平移1个单位长度后的坐标为(m+2,2m),
∵点正好落在轴上,
∴m+2=0,
∴m=-2,
故答案为:-2.
【分析】先求出平移后的坐标为(m+2,2m),再根据y轴上的点坐标的特征可得m+2=0,再求出m的值即可.
15.【答案】解:如图,点C可以为(1,3),(5,3),(2,4),(3,1),(3,5),(4,2).
【解析】【分析】根据A、B点间的水平距离和竖直距离都是1,找出使AC或BC为2的点C即可.
16.【答案】(1)解:点A的坐标为,点A在轴上,
,
,
∴,
点A的坐标为;
(2)解:点A到轴的距离为,
,
解得或,
当时,点A的坐标为;
当时,点A的坐标为.
综上所述,点A的坐标为或.
【解析】【分析】(1)根据y轴上的点的坐标特征可列出方程,解方程即可求出答案。
(2)根据点到x轴的距离性质列出含绝对值的等式,解等式即可求出答案。
17.【答案】解:由图中坐标系可知各点的坐标为:A(﹣2,0),B(2,0),C(1,2),D(0,4),E(﹣1,2),F(0,2),
O(0,0).
【解析】【分析】直接根据图示,在网格中数出对应的点的坐标即可.
18.【答案】解:∵轴,
∴,
∴.
∴点M的坐标为.
【解析】【分析】由轴,可得M、N的横坐标相等,据此解答即可.
19.【答案】(1)点P在x轴上,,
点P坐标为.
(2)点P的纵坐标比横坐标大5,,
点P坐标为.
(3)轴,,
,
∴点P坐标为.
【解析】【分析】(1)平面直角坐标系中,坐标轴上点的特征是:x轴上点的纵坐标均为0,y轴上横坐标均为0;
(2)由纵坐标比横坐标大5,既可以得到“纵坐标=横坐标+5”的等式,即关于m的一元一次方程,求解出m的值,回代即可;
(3)平面直角坐标系中,和坐标轴平行的直线上的点是:和x轴平行的直线上所有的点,纵坐标均相同;和y轴平行的直线上的所有的点,横坐标均相等.因此本题中,点P的横坐标和A的横坐标相同,均为3,列式求解即可.
20.【答案】(1)解:如图,以大门为坐标原点建立坐标系,
则满足旗杆的位置是(-2,3),实验室的位置是(1,4)
(2)(-5,5);(2,5)
(3)解:根据办公楼的位置是(-2,1),教学楼的位置是(2,2),描点如图所示
【解析】【分析】(1)根据“旗杆”和“实验室”的坐标直接建立平面直角坐标系即可;
(2)根据平面直角坐标系直接写出“食堂”和“图书馆”的坐标即可;
(3)在平面直角坐标系中直接写出“办公楼”和“教学楼”的位置即可。
21.【答案】(1)1;0;-4;4
(2)解:由坐标可知,是由向左平移个单位,向上平移个单位得到;
(3)解:
由题意,,
解得:
∴,.
【解析】【解答】解:(1)观察图形可知A的坐标为(1,0), A' 的坐标为(-4,4).
故答案为:1;0;-4;4;
【分析】(1)根据点的位置写出坐标即可;
(2)利用平移变换的性质判断即可;
(3)利用平移变换的性质,构建方程组求解.
1 / 1
一、选择题
1.如果把电影票上“5排3座”记作,那么表示( )
A.“4排4座” B.“9排4座” C.“4排9座” D.“9排9座”
2.在平面直角坐标系中,点P(,2)位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.点A(﹣1,2)到x轴的距离是( )
A.﹣1 B.1 C.﹣2 D.2
4.某气象台为了预报台风,首先需要确定台风中心的位置,则下列说法能确定台风中心位置的是( )
A.北纬 B.距气象台海里
C.北纬,东经 D.北海市附近
5.已知点Q的坐标为 ,点P的坐标为 ,若直线 轴,则点P的坐标为( )
A. B. C. D.
6.如图,小明从点O出发,先向西走400m,再向南走300m到达点M,如果点M的位置用(-4,-3)表示,那么(1,2)表示的位置是( )
A.点A B.点B C.点C D.点D
7.点P(m+3,m﹣2)在直角坐标系的x轴上,则点P的坐标为( )
A.(0,5) B.(5,0) C.(﹣5,0) D.(0,﹣5)
8.如图,关于小明家相对于学校的位置,下列描述最正确的是( )
A.在距离学校米处 B.在学校的东南方向
C.在南偏东方向米处 D.在学校北偏西方向米处
9.在平面直角坐标系中,将三角形各点的纵坐标都减去3,横坐标保持不变,所得图形与原图形相比 ( )
A.向右平移了3个单位 B.向左平移了3个单位
C.向上平移了3个单位 D.向下平移了3个单位
10.如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次平移,每次移动一个单位,得到点,,,,…,那么点的坐标为( )
A. B. C. D.
二、填空题
11.在我市体育馆一侧的座位上,6排3号记为(6,3),则5排8号记为 .
12.在平面直角坐标系中,若点在第一象限,则的取值范围为 .
13.以水平数轴的原点为圆心,过正半轴上的每一刻度点画同心圆,将逆时针依次旋转、、、、得到条射线,构成如图所示的“圆”坐标系,点、的坐标分别表示为、,则点的坐标表示为 .
14.把点向右平移1个单位长度后,点正好落在轴上,则的值为 .
三、解答题
15.如图,正方形网格中的交点,我们称之为格点,点A用有序数对(2,2)表示,其中第一个数表示排数,第2个数表示列数,在图中有一个格点C,使S△ABC=1,写出符合条件的点C的有序数对.
16.已知在平面直角坐标系中,点A的坐标为.
(1)若点A在轴上,求出点A的坐标;
(2)若点A到轴的距离为,求出点A的坐标.
17.如图所示,求出A,B,C,D,E,F,O点的坐标.
18.在平面直角坐标系中,点M的坐标为,点N的坐标为.若轴,求点M的坐标.
19.已知点请分别根据下列条件,求出点P的坐标.
(1)点P在x轴上;
(2)点P的纵坐标比横坐标大5;
(3)点P在过点且与y轴平行的直线上.
20.如图是某学校的平面示意图,已知旗杆的位置是(-2,3),实验室的位置是(1,4)
(1)根据所给条件在图中建立适当的平面直角坐标系;
(2)用坐标表示位置:食堂 ,图书馆 .
(3)已知办公楼的位置是(-2,1),教学楼的位置是(2,2),在图中标出办公楼和教学楼的位置;
21.在平面直角坐标系中,经过平移得到,位置如图所示.
(1)分别写出点,的坐标:( , ),( , ).
(2)请说明是由经过怎样的平移得到的;
(3)若点是内部的一点,则平移后对应点的坐标为,求和的值.
答案解析部分
1.【答案】C
【解析】【解答】解:“5排3座”记作,
表示“4排9座”.
故答案为:C.
【分析】由已知有序数对知:横坐标表示排数,纵坐标表示座号,从而得解.
2.【答案】B
【解析】【解答】P(,2)位于第二象限,
故答案为:B
【分析】根据各象限内点的坐标的符号特征:第一象限(+,+)第二象限(-,+)第三象限(-,-)第四象限(+,-),据此判断即可.
3.【答案】D
【解析】【解答】解:点P(-1,2)到x轴的距离是2.
故答案为:D.
【分析】根据点到x轴的距离等于在这边的绝对值解答即可。
4.【答案】C
【解析】【解答】解:A、不能确定台风中心位置,故A不符合题意;
B、不能确定台风中心位置,故B不符合题意;
C、能确定台风中心位置,故C符合题意;
D、不能确定台风中心位置,故D不符合题意.
故答案为:C.
【分析】 根据确定一个物体的位置需要两个量,逐项进行判断,即可得出答案.
5.【答案】C
【解析】【解答】解:∵点Q的坐标为(2,-3),点P的坐标为(2a+2,a-5),直线PQ⊥y轴,
∴a-5=-3,
∴a=2,
∴2a+2=6,
∴点P的坐标为(6,-3).
故答案为:C.
【分析】根据垂直于y轴的直线所有点的纵坐标相等即可求得a的值,即可得出答案.
6.【答案】B
【解析】【解答】解:∵点M的位置用( 4, 3)表示,实际意义为从点O出发,先向西走400m,再向南走300m,也就是网格中一个小正方形边长为100m,
∴(1,2)表示的位置实际意义为先向东走100m,再向北走200m,对应的是点B,
故答案为:B.
【分析】根据有序数对的表示方法求解即可。
7.【答案】B
【解析】【解答】解:∵点P在直角坐标系的x轴上,
∴m﹣2=0,
∴m=2,
故点P的横坐标为:m+3=2+3=5,
即点P的坐标为(5,0)
故选B.
【分析】由点P在直角坐标系的x轴上得出m﹣2=0,可求出m的值,然后求出点P的坐标即可.
8.【答案】D
【解析】【解答】解:根据图形中的数据可得:小明家在学校北偏西45°方向300米处,
故答案为:D.
【分析】根据图形中的数据直接求出答案即可.
9.【答案】D
【解析】【解答】将三角形各点的纵坐标都减去3,横坐标保持不变,所得图形与原图形相比向下平移了3个单位.
故选:D.
【分析】根据平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减,可得答案.
10.【答案】A
【解析】【解答】解:由图象可知:每移动4次图象完成一个循环,每个循环结束图象向右移动2个单位,
∵2023÷4=505······3,
∴点A的坐标为(505×2+1,0),即(1011,0),
故答案为:A.
【分析】由图象可知:每移动4次图象完成一个循环,每个循环结束图象向右移动2个单位,据此解答即可.
11.【答案】(5,8)
【解析】【解答】解:∵6排3号记为(6,3),
∴5排8号记为(5,8),
故答案为:(5,8).
【分析】根据有序数对的定义求解即可。
12.【答案】
【解析】【解答】∵点在第一象限,
∴,解得,
故答案为:.
【分析】根据点坐标与象限的关系可得不等式组,再求出m的取值范围即可。
13.【答案】(3,240°)
【解析】【解答】解: ∵点、的坐标分别表示为、,
∴圆所在的层数表示横坐标,射线对应的度数表示纵坐标,
∴C(3,240°);
故答案为:(3,240°).
【分析】观察图形及点A、B的坐标,可知圆所在的层数表示横坐标,射线对应的度数表示纵坐标,据此即可求解.
14.【答案】
【解析】【解答】将点P向右平移1个单位长度后的坐标为(m+2,2m),
∵点正好落在轴上,
∴m+2=0,
∴m=-2,
故答案为:-2.
【分析】先求出平移后的坐标为(m+2,2m),再根据y轴上的点坐标的特征可得m+2=0,再求出m的值即可.
15.【答案】解:如图,点C可以为(1,3),(5,3),(2,4),(3,1),(3,5),(4,2).
【解析】【分析】根据A、B点间的水平距离和竖直距离都是1,找出使AC或BC为2的点C即可.
16.【答案】(1)解:点A的坐标为,点A在轴上,
,
,
∴,
点A的坐标为;
(2)解:点A到轴的距离为,
,
解得或,
当时,点A的坐标为;
当时,点A的坐标为.
综上所述,点A的坐标为或.
【解析】【分析】(1)根据y轴上的点的坐标特征可列出方程,解方程即可求出答案。
(2)根据点到x轴的距离性质列出含绝对值的等式,解等式即可求出答案。
17.【答案】解:由图中坐标系可知各点的坐标为:A(﹣2,0),B(2,0),C(1,2),D(0,4),E(﹣1,2),F(0,2),
O(0,0).
【解析】【分析】直接根据图示,在网格中数出对应的点的坐标即可.
18.【答案】解:∵轴,
∴,
∴.
∴点M的坐标为.
【解析】【分析】由轴,可得M、N的横坐标相等,据此解答即可.
19.【答案】(1)点P在x轴上,,
点P坐标为.
(2)点P的纵坐标比横坐标大5,,
点P坐标为.
(3)轴,,
,
∴点P坐标为.
【解析】【分析】(1)平面直角坐标系中,坐标轴上点的特征是:x轴上点的纵坐标均为0,y轴上横坐标均为0;
(2)由纵坐标比横坐标大5,既可以得到“纵坐标=横坐标+5”的等式,即关于m的一元一次方程,求解出m的值,回代即可;
(3)平面直角坐标系中,和坐标轴平行的直线上的点是:和x轴平行的直线上所有的点,纵坐标均相同;和y轴平行的直线上的所有的点,横坐标均相等.因此本题中,点P的横坐标和A的横坐标相同,均为3,列式求解即可.
20.【答案】(1)解:如图,以大门为坐标原点建立坐标系,
则满足旗杆的位置是(-2,3),实验室的位置是(1,4)
(2)(-5,5);(2,5)
(3)解:根据办公楼的位置是(-2,1),教学楼的位置是(2,2),描点如图所示
【解析】【分析】(1)根据“旗杆”和“实验室”的坐标直接建立平面直角坐标系即可;
(2)根据平面直角坐标系直接写出“食堂”和“图书馆”的坐标即可;
(3)在平面直角坐标系中直接写出“办公楼”和“教学楼”的位置即可。
21.【答案】(1)1;0;-4;4
(2)解:由坐标可知,是由向左平移个单位,向上平移个单位得到;
(3)解:
由题意,,
解得:
∴,.
【解析】【解答】解:(1)观察图形可知A的坐标为(1,0), A' 的坐标为(-4,4).
故答案为:1;0;-4;4;
【分析】(1)根据点的位置写出坐标即可;
(2)利用平移变换的性质判断即可;
(3)利用平移变换的性质,构建方程组求解.
1 / 1
