五年级下册数学人教版《3的倍数的特征》课件(共20张PPT)
文档属性
| 名称 | 五年级下册数学人教版《3的倍数的特征》课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 11:39:29 | ||
图片预览








文档简介
(共20张PPT)
《3的倍数的特征》教学及思考
3的倍数特征
教材分析
数学认知
“3的倍数的特征”是《因数和倍数》这一单元的内容。2、5、3 的倍数的特征既是自然数知识的深化,又是接下来要学习的分数单元的重要基础,能帮助学生更便捷地判断一个数是质数还是合数。另外,学习“3 的倍数的特征”,还要对呈现出来的规律进行探索。
从数学认知的角度看,借助 2、5、3 的倍数的特征能促进学生对因数与倍数概念的理解,更有利于认识整数的特点。需要学习者具有一定的数学学及逻辑分析能力。
课前思考
学生在一年级认数、数数时已经会 2 个 2 个地数、5 个 5 个地数,因此在百数表中找 2、5 的倍数比较容易。2、5 的倍数在百数表中一列列地呈现,比较容易发现特征;而“3的倍数的特征”更具隐蔽性,如何引导学生拨开“云雾”,探寻本质,是本课教学的一大难点。
困难点
一方面,部分学生会受到“2、5 的倍数的特征”的负迁移,认为判断一个数是否是 3 的倍数只要看个位;另一方面,学生不清楚“特征”的含义,他们误把“现象”当成“本质”,把“规律”当成“特征”。
让学生明白什么是“特征”,并尝试理解该特征背后的原理
课前调查
学生对“2、5的倍数的特征”了然于胸,而对特征背后的道理却支支吾吾,表述模糊不清,有的则明确表示没有思考过,但超过半数的学生对背后的原理是很感兴趣的。
课前调研问题
3的倍数的特征是什么?和 2、5 的倍数的特征有什么联系与区别?为什么会有这样的特征?研究 3的倍数的特征有什么用?
教学中我们如何基于学生立场,寻找破解疑难之道呢?
【共读期刊||由“爱在小学数学”公众号组织】
百数表”作为研究“2、5的倍数特征”的学习材料,是非常便于学生观察特征、发现规律的,但学生不容易通过圈数来发现“3 的倍数的特征”。一是“3的倍数的特征”本身比较复杂;二是“百数表”中 3 的倍数并不像 2、5 的倍数那样都在同一列,33 个 3 的倍数分散在每一列中,不易聚焦,探索、发现特征无疑就增加了难度。
很多学生对 3 的倍数特征背后的原理很感兴趣,而在教学中教师往往更关注“是什么”,却忽视了让学生了解“为什么”。
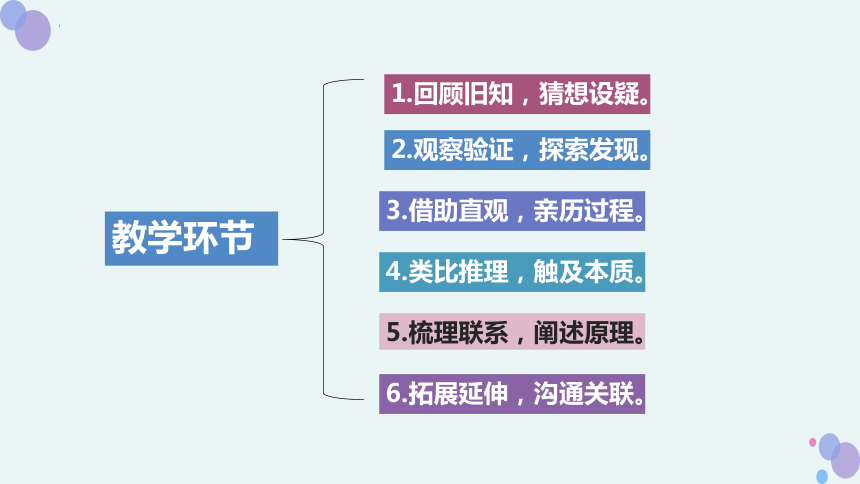
1.回顾旧知,猜想设疑。
2.观察验证,探索发现。
3.借助直观,亲历过程。
4.类比推理,触及本质。
5.梳理联系,阐述原理。
6.拓展延伸,沟通关联。
教学环节
1.回顾旧知,猜想设疑。
步骤一:提问①:2的倍数有什么特征?如何判断一个数是不是 2的倍数?
问题②:5的倍数有什么特征?如何判断一个数是不是 5的倍数?
(引导概括:判断2、5的倍数都是只要看个位。)
抛新③:2、5的倍数特征我们都掌握了,3的倍数有什么特征?
步骤二:猜想:3 的倍数是否也具有这样的特征呢?
观察:观察百数表中 3的倍数,
学生的猜想①:从 3 数起,依次加 3,得到的数就是 3 的倍数;
②3 个3 个地增加;3 依次乘 1、乘 2、乘 3……得到的结果;
③一奇一偶的规律(如 3、6、9、12……);
④3 的倍数在表中都是斜着的。
2.观察验证,探索发现。
①激发疑问:“看来,3 的倍数仅仅看个位是不行的,到底有什么特征呢?”
②引导转换:把各个数位上的数字相加,发现和都是3的倍数。虽然这一结论适合百以内的3的倍数特征,但是否适合所有的自然数?我们的这一猜想到底对不对呢?
③动手验证:请大家选择一些更大的数据进行更全面的验证
④发现反馈:如果一个数各位上的数的和是3的倍数,那么这个数就是3的倍数;如果一个数不是3的倍数,那么这个数各位上的数的和就不是3的倍数。
3.借助直观,亲历过程。
“为什么判断一个数是否是 2、5 的倍数只要看个位呢?”
①举例:
以 232 为例,这是一个三位数,除了个位,还有十位和百位,这两个位上的数为什么不用看?可以画一画、算一算、写一写。
②探究:
学生笔算 232÷2 或 232÷5 时十位余 1 或 3,进而引发新的困惑:是啊,十位都有余数,而且余数不同,为什么只需要看个位就能判断是否是 2或 5 的倍数呢?学生习惯把一个数看成整体进行平均分,显然是除法运算的思维。有的学生认为,232 的百位和十位合起来是23 个十,23 个十是 25 的倍数,所以判断一个数是否是 2、5 的倍数只要看个位就行;还有的学生分开看,200和 30都是 2、5的倍数,所以只看个位就行。
③发现:
看来这些学生有了拆分的意识:即把 232看成 23个十和 2,或者分成 200+30+2
3.借助直观,亲历过程。
要感悟 2、5、3 的倍数特征的本质,需要把各个数位独立进行平均分,关注每一个数位上的余数,也就是说,在各个数位上,每个计数单位也要独立进行平均分。
那么,如何让学生从平均分计数单位的意义
来思考问题呢?借助课件演示
(如图 1)
3.借助直观,亲历过程。
百位上 1个百 1个百地逐个拆分,十位上 1个十 1 个十地逐个拆分。让学生在拆分中体会:百位上不管是几个 100,每个 100 除以 2 都能分完且没有剩余,余数一定是 0;十位也是一样,不管是几个十除以 2,余数也一定是 0;而个位上的数除以 2,有时候余 1,有时候没有余数,所以余数的情况不能确定。
同理,结合课件通过平均分计数单位演示232÷5 的拆分结果,进而明确:不论几个百、几个十除以 5,余数也一定是 0;而个位上的数除以 5,余数可能是 1、2、3、4,有时候没有余数,所以余数的情况也不能确定(如图 2)
4.类比推理,触及本质。
3 的倍数的特征背后的数学依据是数论中同余的基本性质,即 a、b关于模 m同余,等价于存在某个整数 q,使 a=b+qm。例如 12=1×10+2=1×(9+1)+2=1×3×3+(1+2),所以 12 和(1+2)关于 3 同余。但这样的演绎论证过程,对于五年级学生来说,理解难度很大。那么,如何让学生了解其本质,明晰知识间的联系,对“3的倍数的特征”获得直观又简明的理解呢?
4.类比推理,触及本质。
借助前面 2、5 的倍数特征探究经验,学生能够类推到 3 的倍数的特征不能只看个位,因为每一位的余数都无法确定,所以每个数位都要看。但是如何把分计数单位和特征形成关联,对学生而言,理解是有难度的。因为学生在二年级学习《有余数的除法》时,余数一定比除数小的结论已根植于内心,对于余数等于或大于除数的情况很难突破思维瓶颈去思考,这就需要引导学生从计数单位考虑。结合下面的图 3,进行动态展示说理。
4.类比推理,触及本质。
在把计数单位一个一个拆分的过程中,让学生体会:百位上每个 100 除以 3 都会多出 1,有几个百就会剩余几个一;十位有几个十,也会多出几个一。即最后只要看数位上的数是几,就会多出几个一。这样就打破了把一个数看成一个整体去平均分的单一思维路径,进而转向从各个数位、计数单位去平均分,促进学生的思维向纵深发展,对 3 的倍数特征的理解更触及知识的本质
5.梳理联系,阐述原理。
如果把上述演示的过程用算式呈现,该怎样表达呢?
232=2×100+3×10+( 2)2×100=200,3×10=30,200 和 30 都是 2、5 的倍数,所以一个数是不是 2、5 的倍数,只要看个位就能判断。
如果继续分解:
232=2×100+3×10+(2)
=2×(99+1)+3×(9+1)+(2)
=2×99+(2)+3×9+(3)+(2)
=2×99+3×9+(2)+(3)+(2)
因为 2×99 和 3×9 一定是 3 的倍数,所以只要
看 2+3+2=7,7 不是 3 的倍数,所以 232 不是 3 的
倍数。再依此类推,判断更大的数是否是 3 的倍数
又该怎样表达呢?
“根据今天学到的知识,你能否说出 9的倍数的特征呢?”有 的 学 生 借 助 前 面 的 拆 分 图 画 图 说 理 ,如图 4。
6.拓展延伸,沟通关联。
百位上每个 100 除以 9 都会多出 1,有几个百就会剩余几个一;十位有几个十,也会多出几个一。即最后只要看该数位上的数是几,就会多出几个一。因此,9 的倍数特征和 3 的倍数特征道理相同。
有的学生直接根据算式推理如下因为 232=2×100+3×10+(2)
=2×(99+1)+3×(9+1)+(2)
=2×99+(2)+3×9+(3)+(2)
=2×99+3×9+(2)+(3)+(2)
其中 2×99+3×9 一定是 9 的倍数,所以 9 的倍数 特 征 和 3 的 倍 数 特 征 一 样 ,只 不 过 要 把 3换成 9。
6.拓展延伸,沟通关联。
感悟 2、5、3 的倍数的特征关键在于怎么分。整除的意义是平均分之后得到的结果是整数而没有余数。学生习惯于把一个数看成整体进行平均分(除法运算的思维),而要感悟 2、5、3 的倍数的特征本质,则需要把各个数位独立进行平均分,关注每一个数位上的余数。进而每个计数单位也要独立进行平均分,这样特征才会凸显。学生在找数—观察—猜想—验证—说理中,逐渐感悟到数学学习的方法。
总结分享
教师在对学情精准诊断的基础上,借助直观的形拓宽了学生的思考路径,打通图与式的通道,让学生探究图、计数单位、算式、倍数之间的关系,体验对比、抽象等思想方法。这既促进了学生对知识的深度理解和有效迁移,又为学有余力的学生探究类似 4、6 等数的倍数的特征做了铺垫。
在透过表象探寻知识本质的过程中,学生对不同的概念进行比较、辨析,纵向把握知识脉络,横向沟通知识联系,深入学习内容的实质,领悟知识背后蕴含的思想方法,培养了理性精神,提升了数学核心素养。
总结分享
感谢齐读
2020
《3的倍数的特征》教学及思考
3的倍数特征
教材分析
数学认知
“3的倍数的特征”是《因数和倍数》这一单元的内容。2、5、3 的倍数的特征既是自然数知识的深化,又是接下来要学习的分数单元的重要基础,能帮助学生更便捷地判断一个数是质数还是合数。另外,学习“3 的倍数的特征”,还要对呈现出来的规律进行探索。
从数学认知的角度看,借助 2、5、3 的倍数的特征能促进学生对因数与倍数概念的理解,更有利于认识整数的特点。需要学习者具有一定的数学学及逻辑分析能力。
课前思考
学生在一年级认数、数数时已经会 2 个 2 个地数、5 个 5 个地数,因此在百数表中找 2、5 的倍数比较容易。2、5 的倍数在百数表中一列列地呈现,比较容易发现特征;而“3的倍数的特征”更具隐蔽性,如何引导学生拨开“云雾”,探寻本质,是本课教学的一大难点。
困难点
一方面,部分学生会受到“2、5 的倍数的特征”的负迁移,认为判断一个数是否是 3 的倍数只要看个位;另一方面,学生不清楚“特征”的含义,他们误把“现象”当成“本质”,把“规律”当成“特征”。
让学生明白什么是“特征”,并尝试理解该特征背后的原理
课前调查
学生对“2、5的倍数的特征”了然于胸,而对特征背后的道理却支支吾吾,表述模糊不清,有的则明确表示没有思考过,但超过半数的学生对背后的原理是很感兴趣的。
课前调研问题
3的倍数的特征是什么?和 2、5 的倍数的特征有什么联系与区别?为什么会有这样的特征?研究 3的倍数的特征有什么用?
教学中我们如何基于学生立场,寻找破解疑难之道呢?
【共读期刊||由“爱在小学数学”公众号组织】
百数表”作为研究“2、5的倍数特征”的学习材料,是非常便于学生观察特征、发现规律的,但学生不容易通过圈数来发现“3 的倍数的特征”。一是“3的倍数的特征”本身比较复杂;二是“百数表”中 3 的倍数并不像 2、5 的倍数那样都在同一列,33 个 3 的倍数分散在每一列中,不易聚焦,探索、发现特征无疑就增加了难度。
很多学生对 3 的倍数特征背后的原理很感兴趣,而在教学中教师往往更关注“是什么”,却忽视了让学生了解“为什么”。
1.回顾旧知,猜想设疑。
2.观察验证,探索发现。
3.借助直观,亲历过程。
4.类比推理,触及本质。
5.梳理联系,阐述原理。
6.拓展延伸,沟通关联。
教学环节
1.回顾旧知,猜想设疑。
步骤一:提问①:2的倍数有什么特征?如何判断一个数是不是 2的倍数?
问题②:5的倍数有什么特征?如何判断一个数是不是 5的倍数?
(引导概括:判断2、5的倍数都是只要看个位。)
抛新③:2、5的倍数特征我们都掌握了,3的倍数有什么特征?
步骤二:猜想:3 的倍数是否也具有这样的特征呢?
观察:观察百数表中 3的倍数,
学生的猜想①:从 3 数起,依次加 3,得到的数就是 3 的倍数;
②3 个3 个地增加;3 依次乘 1、乘 2、乘 3……得到的结果;
③一奇一偶的规律(如 3、6、9、12……);
④3 的倍数在表中都是斜着的。
2.观察验证,探索发现。
①激发疑问:“看来,3 的倍数仅仅看个位是不行的,到底有什么特征呢?”
②引导转换:把各个数位上的数字相加,发现和都是3的倍数。虽然这一结论适合百以内的3的倍数特征,但是否适合所有的自然数?我们的这一猜想到底对不对呢?
③动手验证:请大家选择一些更大的数据进行更全面的验证
④发现反馈:如果一个数各位上的数的和是3的倍数,那么这个数就是3的倍数;如果一个数不是3的倍数,那么这个数各位上的数的和就不是3的倍数。
3.借助直观,亲历过程。
“为什么判断一个数是否是 2、5 的倍数只要看个位呢?”
①举例:
以 232 为例,这是一个三位数,除了个位,还有十位和百位,这两个位上的数为什么不用看?可以画一画、算一算、写一写。
②探究:
学生笔算 232÷2 或 232÷5 时十位余 1 或 3,进而引发新的困惑:是啊,十位都有余数,而且余数不同,为什么只需要看个位就能判断是否是 2或 5 的倍数呢?学生习惯把一个数看成整体进行平均分,显然是除法运算的思维。有的学生认为,232 的百位和十位合起来是23 个十,23 个十是 25 的倍数,所以判断一个数是否是 2、5 的倍数只要看个位就行;还有的学生分开看,200和 30都是 2、5的倍数,所以只看个位就行。
③发现:
看来这些学生有了拆分的意识:即把 232看成 23个十和 2,或者分成 200+30+2
3.借助直观,亲历过程。
要感悟 2、5、3 的倍数特征的本质,需要把各个数位独立进行平均分,关注每一个数位上的余数,也就是说,在各个数位上,每个计数单位也要独立进行平均分。
那么,如何让学生从平均分计数单位的意义
来思考问题呢?借助课件演示
(如图 1)
3.借助直观,亲历过程。
百位上 1个百 1个百地逐个拆分,十位上 1个十 1 个十地逐个拆分。让学生在拆分中体会:百位上不管是几个 100,每个 100 除以 2 都能分完且没有剩余,余数一定是 0;十位也是一样,不管是几个十除以 2,余数也一定是 0;而个位上的数除以 2,有时候余 1,有时候没有余数,所以余数的情况不能确定。
同理,结合课件通过平均分计数单位演示232÷5 的拆分结果,进而明确:不论几个百、几个十除以 5,余数也一定是 0;而个位上的数除以 5,余数可能是 1、2、3、4,有时候没有余数,所以余数的情况也不能确定(如图 2)
4.类比推理,触及本质。
3 的倍数的特征背后的数学依据是数论中同余的基本性质,即 a、b关于模 m同余,等价于存在某个整数 q,使 a=b+qm。例如 12=1×10+2=1×(9+1)+2=1×3×3+(1+2),所以 12 和(1+2)关于 3 同余。但这样的演绎论证过程,对于五年级学生来说,理解难度很大。那么,如何让学生了解其本质,明晰知识间的联系,对“3的倍数的特征”获得直观又简明的理解呢?
4.类比推理,触及本质。
借助前面 2、5 的倍数特征探究经验,学生能够类推到 3 的倍数的特征不能只看个位,因为每一位的余数都无法确定,所以每个数位都要看。但是如何把分计数单位和特征形成关联,对学生而言,理解是有难度的。因为学生在二年级学习《有余数的除法》时,余数一定比除数小的结论已根植于内心,对于余数等于或大于除数的情况很难突破思维瓶颈去思考,这就需要引导学生从计数单位考虑。结合下面的图 3,进行动态展示说理。
4.类比推理,触及本质。
在把计数单位一个一个拆分的过程中,让学生体会:百位上每个 100 除以 3 都会多出 1,有几个百就会剩余几个一;十位有几个十,也会多出几个一。即最后只要看数位上的数是几,就会多出几个一。这样就打破了把一个数看成一个整体去平均分的单一思维路径,进而转向从各个数位、计数单位去平均分,促进学生的思维向纵深发展,对 3 的倍数特征的理解更触及知识的本质
5.梳理联系,阐述原理。
如果把上述演示的过程用算式呈现,该怎样表达呢?
232=2×100+3×10+( 2)2×100=200,3×10=30,200 和 30 都是 2、5 的倍数,所以一个数是不是 2、5 的倍数,只要看个位就能判断。
如果继续分解:
232=2×100+3×10+(2)
=2×(99+1)+3×(9+1)+(2)
=2×99+(2)+3×9+(3)+(2)
=2×99+3×9+(2)+(3)+(2)
因为 2×99 和 3×9 一定是 3 的倍数,所以只要
看 2+3+2=7,7 不是 3 的倍数,所以 232 不是 3 的
倍数。再依此类推,判断更大的数是否是 3 的倍数
又该怎样表达呢?
“根据今天学到的知识,你能否说出 9的倍数的特征呢?”有 的 学 生 借 助 前 面 的 拆 分 图 画 图 说 理 ,如图 4。
6.拓展延伸,沟通关联。
百位上每个 100 除以 9 都会多出 1,有几个百就会剩余几个一;十位有几个十,也会多出几个一。即最后只要看该数位上的数是几,就会多出几个一。因此,9 的倍数特征和 3 的倍数特征道理相同。
有的学生直接根据算式推理如下因为 232=2×100+3×10+(2)
=2×(99+1)+3×(9+1)+(2)
=2×99+(2)+3×9+(3)+(2)
=2×99+3×9+(2)+(3)+(2)
其中 2×99+3×9 一定是 9 的倍数,所以 9 的倍数 特 征 和 3 的 倍 数 特 征 一 样 ,只 不 过 要 把 3换成 9。
6.拓展延伸,沟通关联。
感悟 2、5、3 的倍数的特征关键在于怎么分。整除的意义是平均分之后得到的结果是整数而没有余数。学生习惯于把一个数看成整体进行平均分(除法运算的思维),而要感悟 2、5、3 的倍数的特征本质,则需要把各个数位独立进行平均分,关注每一个数位上的余数。进而每个计数单位也要独立进行平均分,这样特征才会凸显。学生在找数—观察—猜想—验证—说理中,逐渐感悟到数学学习的方法。
总结分享
教师在对学情精准诊断的基础上,借助直观的形拓宽了学生的思考路径,打通图与式的通道,让学生探究图、计数单位、算式、倍数之间的关系,体验对比、抽象等思想方法。这既促进了学生对知识的深度理解和有效迁移,又为学有余力的学生探究类似 4、6 等数的倍数的特征做了铺垫。
在透过表象探寻知识本质的过程中,学生对不同的概念进行比较、辨析,纵向把握知识脉络,横向沟通知识联系,深入学习内容的实质,领悟知识背后蕴含的思想方法,培养了理性精神,提升了数学核心素养。
总结分享
感谢齐读
2020
