福建长乐七中2009届高三数学理科模拟卷
文档属性
| 名称 | 福建长乐七中2009届高三数学理科模拟卷 |

|
|
| 格式 | rar | ||
| 文件大小 | 234.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-05-04 00:00:00 | ||
图片预览



文档简介
福建长乐七中2009届高三数学理科模拟卷 于5月
数学(理科)试卷
本试卷分第1卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第21题(1)、(2)、(3)题为选考题,本剧要求选答;其他题为必考题,本卷满分150分,考试时间120分钟·21世纪教育网
参考公式:21世纪教育网
锥体的体积公式: ,其中S为底面面积,h为高;21世纪教育网
球的表面积、体积公式: 其中r为球的半径.21世纪教育网
第Ⅰ卷(选择题共50分)21世纪教育网
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中有
且仅有一项是符合题目要求的.把答案填涂在答题卡的相应位置
1.已知,i是虚数单位,若,则复数x+2i共轭复数是( )
A. B. C. D.
2.已知向量,若,则锐角等于( )
A. B. C. D.
3.已知集合,,则( )
A. B. C. D.
4.阅读右边的流程图,若输入的a、b、c分别是11、22、33,
则输出的a、b、c分别是:( )
A.33、11、22 B.11、22、33
C.22、11、33 D.33、22、11
5.已知为两条不同的直线,为两个不同的平面,
则下列命题中正确的是( )
A.
B.
C.
D.
6.如图,边长为2的正方形内有一内切圆.在图形上随机
投掷一个点,则该点落到圆内的概率是( )
A. B. C. D.
7.“”是“直线”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
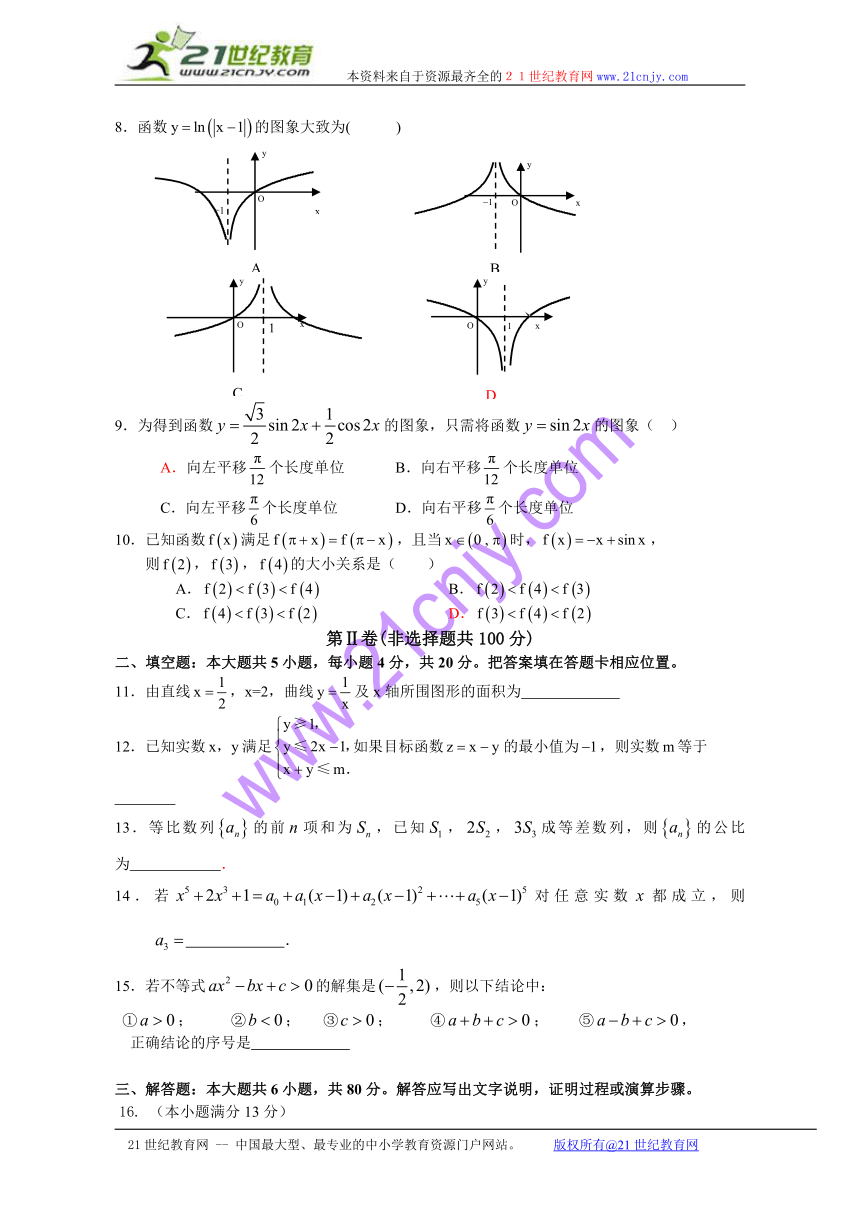
8.函数的图象大致为( )
9.为得到函数的图象,只需将函数的图象( )
A.向左平移个长度单位 B.向右平移个长度单位
C.向左平移个长度单位 D.向右平移个长度单位
10.已知函数满足,且当时,,
则,,的大小关系是( )
A. B.
C. D.
第Ⅱ卷(非选择题共100分)
二、填空题:本大题共5小题,每小题4分,共20分。把答案填在答题卡相应位置。
11.由直线,x=2,曲线及x轴所围图形的面积为
12.已知实数满足如果目标函数的最小值为,则实数等于
13.等比数列的前项和为,已知,,成等差数列,则的公比为 .
14.若对任意实数都成立,则 .
15.若不等式的解集是,则以下结论中:
①; ②; ③; ④; ⑤,
正确结论的序号是
三、解答题:本大题共6小题,共80分。解答应写出文字说明,证明过程或演算步骤。
16. (本小题满分13分)
已知:函数的周期为,且当时,函数的最小值为0.
(1)求函数的表达式;
(2)在△ABC中,若,且2sin2B=cosB+cos(A-C),求 的值.
17.(本小题满分13分)
甲、乙两名同学参加一项射击游戏,两人约定,其中任何一人每射击一次,击中目标得2分,未击中目标得0分.若甲、乙两名同学射击的命中率分别为和p ,且甲、乙两人各射击一次所得分数之和为2的概率为,假设甲、乙两人射击互不影响.
(1)求p的值;
(2) 记甲、乙两人各射击一次所得分数之和为ξ,求ξ的分布列和数学期望.
18. (本小题满分13分)
如图,正方形与正方形所在平面互相垂直,为的中点,
(Ⅰ)若为线段上的中点,求证:平面;
(Ⅱ)求二面角的余弦值;
19.(本小题满分13分)
在平面直角坐标系中,经过点且斜率为的直线与椭圆有两个不同的交点和.
(I)求的取值范围;
( II)设椭圆与轴正半轴、轴正半轴的交点分别为,是否存在常数,使得向量与垂直?如果存在,求值;如果不存在,请说明理由.
20.(本小题满分14分)
已知函数.
(1)当时,求函数的单调区间和极值;
(2)当时,若,均有,求实数的取值范围;
(3)若,,且,试比较与的大小.
21.本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分。
如果多做,则按所做的前两题计分。
(1)(本小题满分7分)选修4-2:矩阵与变换
已知,,试求的特征值以及属于每个特征值的一个特征向量.
(2)(本小题满分7分)选修4-4:坐标系与参数方程
在曲线上求一点,使它到直线
的距离最小,并求出该点坐标和最小距离。
(3)(本小题满分7分)选修4-5;不等式选讲
若。
评分标准与参考答案
一、DCBAD CADAD
二、11.2ln2 12. 5 13. 14. 12 15. ②③⑤
三、
16.(1)解:∵ ,T=,
即.……………3分
∵[0,] , ∴≤≤ ∴≤≤1
∴的最小值为m,∴m=0
即 ………………………………7分
(2)=2 ∴
而∠(0,), ∴∠= …………………………9 分
在△ABC中,∵A+B=,2sin2B=cosB+cos(A-C)
∴ 2cos2A-sinA-sinA=0 解得sinA=
∵0 ,∴ sinA= ……………………13分
17. 解:(1)设“甲射击一次,击中目标”为事件A,“乙射击一次,击中目标”为事件B,“甲射击一次,未击中目标”为事件,“乙射击一次,未击中目标”为事件,则
……1分
依题意得, ……3分
解得,故p的值为. ……5分
(2)ξ的取值分别为0,2,4. ……6分
, ……8分
,
,
∴ξ的分布列为
ξ
0
2
4
P
……11分
∴Eξ= ……13分
18. 解法一:(几何法)
(Ⅰ)连结,则是的中点,
在△中,,
且平面,平面,
∴∥平面
(Ⅱ)取中点
即,
解法二:(向量法)以点为原点,为轴,建系如图
,
(Ⅰ)若为线段上的中点,
则,
,
∴ ∥平面 ………………………………6’
(Ⅱ)易知平面的法向量……………………7’
设平面的法向量 , 由
解得 …………………9’
,
……………………13’
19.解:(Ⅰ)由已知条件,直线的方程为,…………………1分
代入椭圆方程得.
整理得 ① …………………2分
直线与椭圆有两个不同的交点和等价于,
…………………………………………………3分
解得或.…………………5分
即的取值范围为.……………6分
(Ⅱ)设,则,
由方程①,. ②
又. ③ ……………7分
而.
所以与垂直等价于,…………9分
将②③代入上式,解得.…………………………11分
由(Ⅰ)知或,故没有符合题意的常数.………………13分
20. 解:由题意, …………………………………………2分
(1)当时,
由得,解得,函数的单调增区间是;
由得,解得,函数的单调增区间是
∴当时,函数有极小值为.………6分
(2)当时,由于,均有,
即,恒成立,
∴,, ……………………………………………………8分
由(1),函数极小值即为最小值,
∴,解得.………………………………10分
(3),
∵且,
∴,
∴,……………………………………………12分
又,∴,
∴,即.……14分
21. (1)解:==, ……………………………1分
矩阵的特征多项式为=,……………………3分
令,得矩阵的特征值为。 ……………………………4分
对于特征值解相应的线性方程组得一个非零解
∴是矩阵的属于特征值的一个特征向量。 ……………6分
对于特征值解相应的线性方程组得一个非零解
∴是矩阵的属于特征值的一个特征向量。 ……………7分
(2)解:直线化成普通方程是………………………2分
设所求的点为P则P到直线的距离
当时,即时,d取最小值1,……5分
此时,点P的坐标是……………………………………………7分
(3)解:根据题意,即,……………………2分
……………………4分
或(舍去)
当且仅当时等号成立,……………7分
数学(理科)试卷
本试卷分第1卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第21题(1)、(2)、(3)题为选考题,本剧要求选答;其他题为必考题,本卷满分150分,考试时间120分钟·21世纪教育网
参考公式:21世纪教育网
锥体的体积公式: ,其中S为底面面积,h为高;21世纪教育网
球的表面积、体积公式: 其中r为球的半径.21世纪教育网
第Ⅰ卷(选择题共50分)21世纪教育网
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中有
且仅有一项是符合题目要求的.把答案填涂在答题卡的相应位置
1.已知,i是虚数单位,若,则复数x+2i共轭复数是( )
A. B. C. D.
2.已知向量,若,则锐角等于( )
A. B. C. D.
3.已知集合,,则( )
A. B. C. D.
4.阅读右边的流程图,若输入的a、b、c分别是11、22、33,
则输出的a、b、c分别是:( )
A.33、11、22 B.11、22、33
C.22、11、33 D.33、22、11
5.已知为两条不同的直线,为两个不同的平面,
则下列命题中正确的是( )
A.
B.
C.
D.
6.如图,边长为2的正方形内有一内切圆.在图形上随机
投掷一个点,则该点落到圆内的概率是( )
A. B. C. D.
7.“”是“直线”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
8.函数的图象大致为( )
9.为得到函数的图象,只需将函数的图象( )
A.向左平移个长度单位 B.向右平移个长度单位
C.向左平移个长度单位 D.向右平移个长度单位
10.已知函数满足,且当时,,
则,,的大小关系是( )
A. B.
C. D.
第Ⅱ卷(非选择题共100分)
二、填空题:本大题共5小题,每小题4分,共20分。把答案填在答题卡相应位置。
11.由直线,x=2,曲线及x轴所围图形的面积为
12.已知实数满足如果目标函数的最小值为,则实数等于
13.等比数列的前项和为,已知,,成等差数列,则的公比为 .
14.若对任意实数都成立,则 .
15.若不等式的解集是,则以下结论中:
①; ②; ③; ④; ⑤,
正确结论的序号是
三、解答题:本大题共6小题,共80分。解答应写出文字说明,证明过程或演算步骤。
16. (本小题满分13分)
已知:函数的周期为,且当时,函数的最小值为0.
(1)求函数的表达式;
(2)在△ABC中,若,且2sin2B=cosB+cos(A-C),求 的值.
17.(本小题满分13分)
甲、乙两名同学参加一项射击游戏,两人约定,其中任何一人每射击一次,击中目标得2分,未击中目标得0分.若甲、乙两名同学射击的命中率分别为和p ,且甲、乙两人各射击一次所得分数之和为2的概率为,假设甲、乙两人射击互不影响.
(1)求p的值;
(2) 记甲、乙两人各射击一次所得分数之和为ξ,求ξ的分布列和数学期望.
18. (本小题满分13分)
如图,正方形与正方形所在平面互相垂直,为的中点,
(Ⅰ)若为线段上的中点,求证:平面;
(Ⅱ)求二面角的余弦值;
19.(本小题满分13分)
在平面直角坐标系中,经过点且斜率为的直线与椭圆有两个不同的交点和.
(I)求的取值范围;
( II)设椭圆与轴正半轴、轴正半轴的交点分别为,是否存在常数,使得向量与垂直?如果存在,求值;如果不存在,请说明理由.
20.(本小题满分14分)
已知函数.
(1)当时,求函数的单调区间和极值;
(2)当时,若,均有,求实数的取值范围;
(3)若,,且,试比较与的大小.
21.本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分。
如果多做,则按所做的前两题计分。
(1)(本小题满分7分)选修4-2:矩阵与变换
已知,,试求的特征值以及属于每个特征值的一个特征向量.
(2)(本小题满分7分)选修4-4:坐标系与参数方程
在曲线上求一点,使它到直线
的距离最小,并求出该点坐标和最小距离。
(3)(本小题满分7分)选修4-5;不等式选讲
若。
评分标准与参考答案
一、DCBAD CADAD
二、11.2ln2 12. 5 13. 14. 12 15. ②③⑤
三、
16.(1)解:∵ ,T=,
即.……………3分
∵[0,] , ∴≤≤ ∴≤≤1
∴的最小值为m,∴m=0
即 ………………………………7分
(2)=2 ∴
而∠(0,), ∴∠= …………………………9 分
在△ABC中,∵A+B=,2sin2B=cosB+cos(A-C)
∴ 2cos2A-sinA-sinA=0 解得sinA=
∵0 ,∴ sinA= ……………………13分
17. 解:(1)设“甲射击一次,击中目标”为事件A,“乙射击一次,击中目标”为事件B,“甲射击一次,未击中目标”为事件,“乙射击一次,未击中目标”为事件,则
……1分
依题意得, ……3分
解得,故p的值为. ……5分
(2)ξ的取值分别为0,2,4. ……6分
, ……8分
,
,
∴ξ的分布列为
ξ
0
2
4
P
……11分
∴Eξ= ……13分
18. 解法一:(几何法)
(Ⅰ)连结,则是的中点,
在△中,,
且平面,平面,
∴∥平面
(Ⅱ)取中点
即,
解法二:(向量法)以点为原点,为轴,建系如图
,
(Ⅰ)若为线段上的中点,
则,
,
∴ ∥平面 ………………………………6’
(Ⅱ)易知平面的法向量……………………7’
设平面的法向量 , 由
解得 …………………9’
,
……………………13’
19.解:(Ⅰ)由已知条件,直线的方程为,…………………1分
代入椭圆方程得.
整理得 ① …………………2分
直线与椭圆有两个不同的交点和等价于,
…………………………………………………3分
解得或.…………………5分
即的取值范围为.……………6分
(Ⅱ)设,则,
由方程①,. ②
又. ③ ……………7分
而.
所以与垂直等价于,…………9分
将②③代入上式,解得.…………………………11分
由(Ⅰ)知或,故没有符合题意的常数.………………13分
20. 解:由题意, …………………………………………2分
(1)当时,
由得,解得,函数的单调增区间是;
由得,解得,函数的单调增区间是
∴当时,函数有极小值为.………6分
(2)当时,由于,均有,
即,恒成立,
∴,, ……………………………………………………8分
由(1),函数极小值即为最小值,
∴,解得.………………………………10分
(3),
∵且,
∴,
∴,……………………………………………12分
又,∴,
∴,即.……14分
21. (1)解:==, ……………………………1分
矩阵的特征多项式为=,……………………3分
令,得矩阵的特征值为。 ……………………………4分
对于特征值解相应的线性方程组得一个非零解
∴是矩阵的属于特征值的一个特征向量。 ……………6分
对于特征值解相应的线性方程组得一个非零解
∴是矩阵的属于特征值的一个特征向量。 ……………7分
(2)解:直线化成普通方程是………………………2分
设所求的点为P则P到直线的距离
当时,即时,d取最小值1,……5分
此时,点P的坐标是……………………………………………7分
(3)解:根据题意,即,……………………2分
……………………4分
或(舍去)
当且仅当时等号成立,……………7分
同课章节目录
