2024年浙江省中考数学模拟练习试卷(含解析)
文档属性
| 名称 | 2024年浙江省中考数学模拟练习试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 23:52:59 | ||
图片预览

文档简介
2024年浙江省中考数学模拟练习试卷
(考试时间:120分钟 试卷满分:120分)
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下图是由一个长方体和一个圆柱组成的几何体,它的俯视图是( )
A. B. C. D.
2.下列计算正确的是( )
A. B. C. D.
截至2022年3月24日,携带“祝融号”火星车的“天问一号”环绕器在轨运行609天,
距离地球277000000千米;数据277000000用科学记数法表示为( )
A. B. C. D.
4.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
5.已知点P(m﹣3,m﹣1)在第二象限,则m的取值范围在数轴上表示正确的是( )
A. B.
C. D.
6.化简的结果是( )
A. B. C. D.
7 .从甲、乙、丙三人中任选两人参加青年志愿者活动,甲被选中的概率是( )
A. B. C. D.
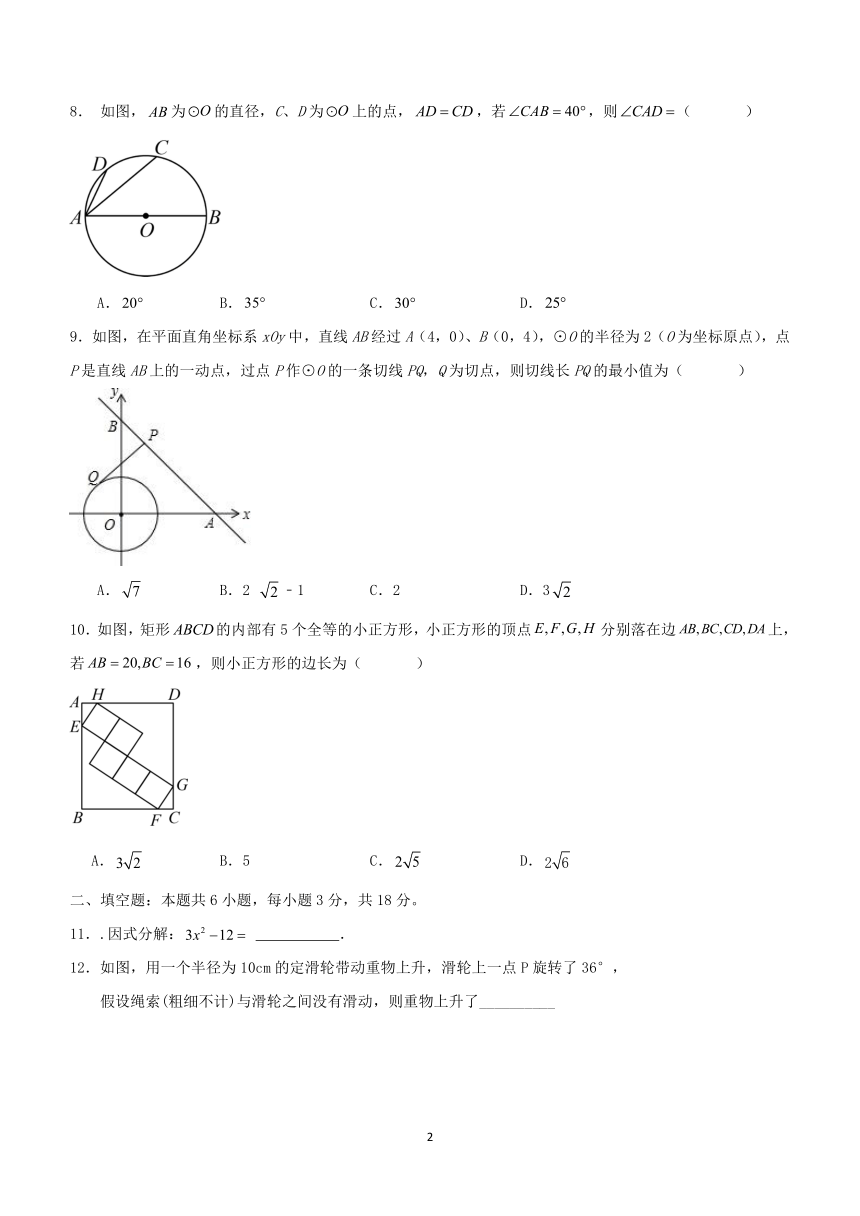
8. 如图,为的直径,C、D为上的点,,若,则( )
A. B. C. D.
9.如图,在平面直角坐标系xOy中,直线AB经过A(4,0)、B(0,4),⊙O的半径为2(O为坐标原点),点P是直线AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
A. B.2 ﹣1 C.2 D.3
10.如图,矩形的内部有5个全等的小正方形,小正方形的顶点分别落在边上,若,则小正方形的边长为( )
A. B.5 C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11..因式分解: .
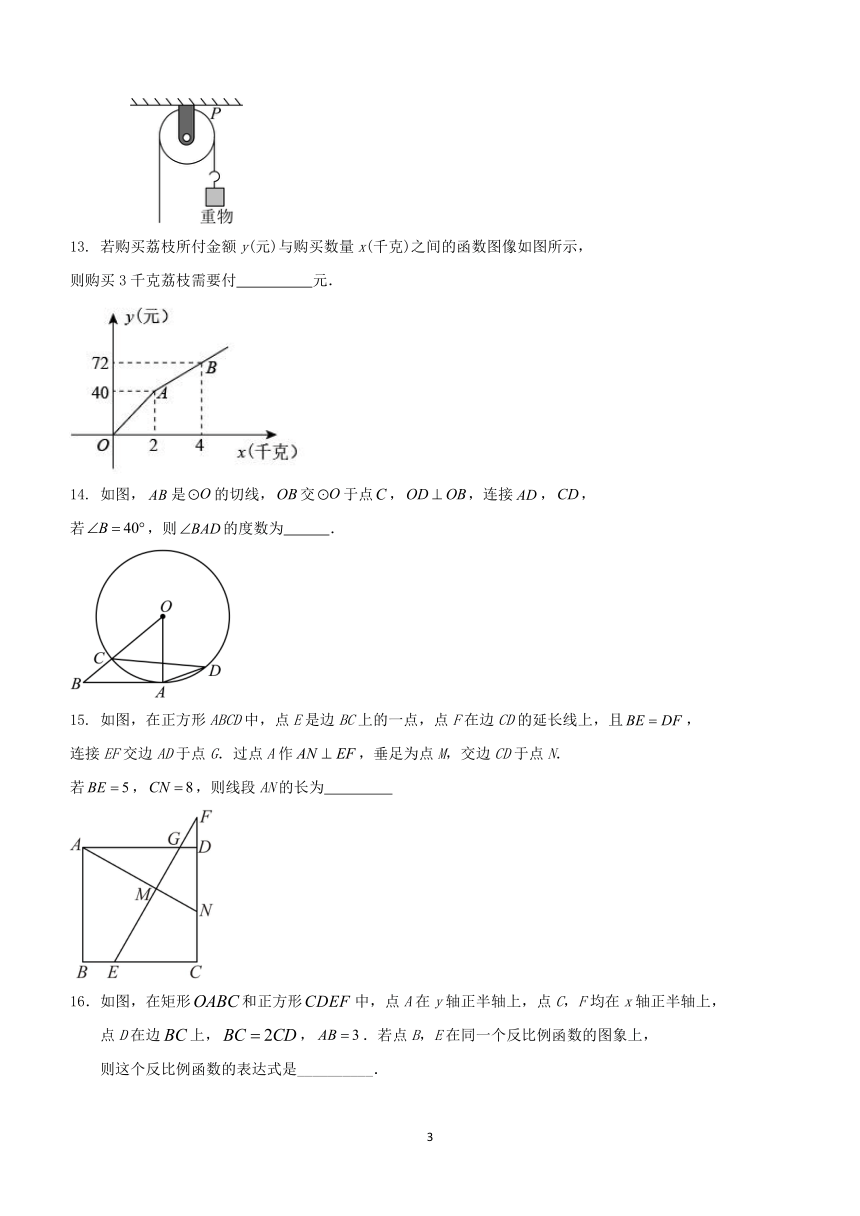
12.如图,用一个半径为10cm的定滑轮带动重物上升,滑轮上一点P旋转了36°,
假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了__________
若购买荔枝所付金额y(元)与购买数量x(千克)之间的函数图像如图所示,
则购买3千克荔枝需要付 元.
如图,是的切线,交于点,,连接,,
若,则的度数为 .
如图,在正方形ABCD中,点E是边BC上的一点,点F在边CD的延长线上,且,
连接EF交边AD于点G.过点A作,垂足为点M,交边CD于点N.
若,,则线段AN的长为
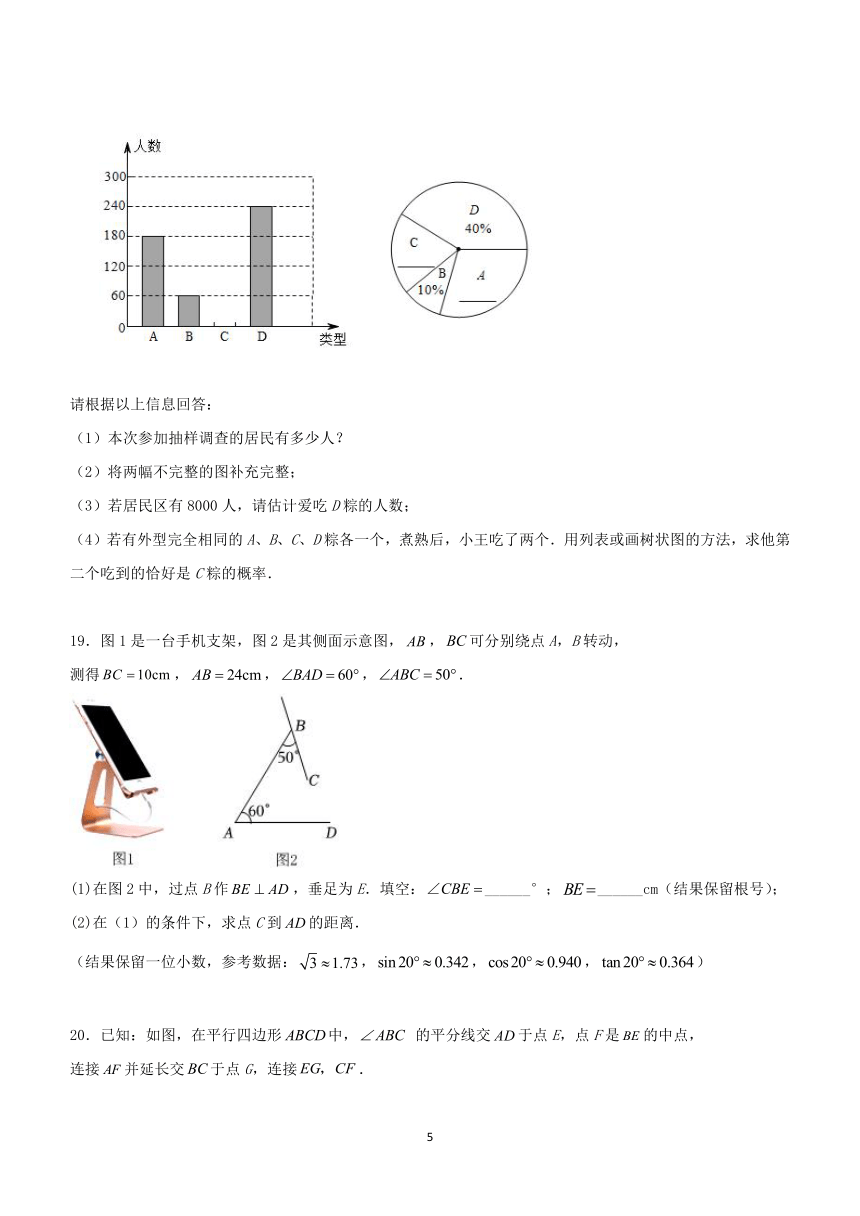
16.如图,在矩形和正方形中,点A在y轴正半轴上,点C,F均在x轴正半轴上,
点D在边上,,.若点B,E在同一个反比例函数的图象上,
则这个反比例函数的表达式是__________.
三、解答题(第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.(1).
(2).
如图,在的网格中,线段的端点都在格点上(两条网格线的交点叫格点).
请用无刻度的直尺画出符合要求的图形,并保留画图痕迹(不要求写画法).
(1)在图1中画出一个以为边的,使顶点在格点上.
(2)在图2中的线段上找出一点,使.
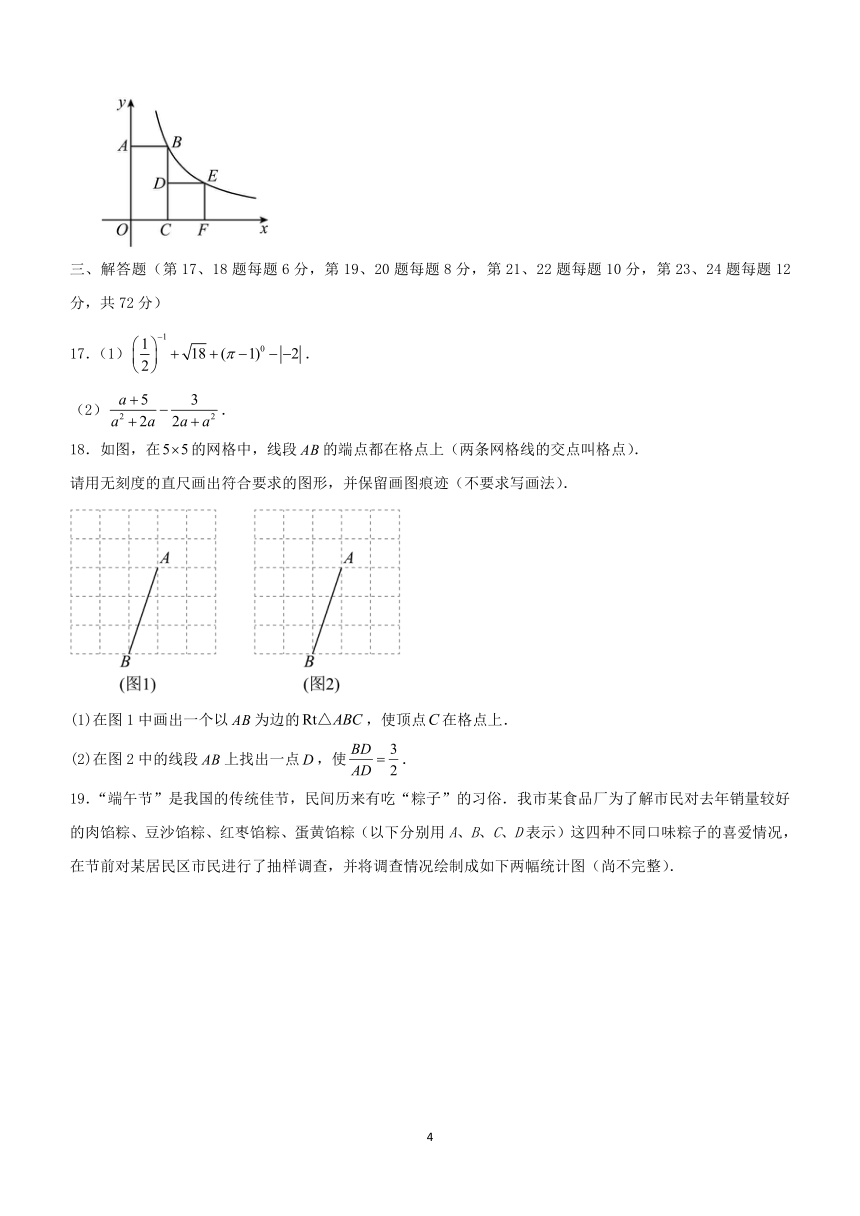
19.“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
图1是一台手机支架,图2是其侧面示意图,,可分别绕点A,B转动,
测得,,,.
(1)在图2中,过点B作,垂足为E.填空:______°;______cm(结果保留根号);
(2)在(1)的条件下,求点C到的距离.
(结果保留一位小数,参考数据:,,,)
已知:如图,在平行四边形中, 的平分线交于点E,点F是的中点,
连接并延长交于点G,连接.
(1)求证:四边形是菱形;
(2)若,,求的长.
22.第19届杭州亚运会,吉祥物为“宸宸”、“琮琮”、“莲莲”,
如图,某校准备举行“第19届亚运会”知识竞赛活动,
拟购买30套吉祥物(“宸宸”、“琮琮”、“莲莲”)作为竞赛奖品.某商店有甲,乙两种规格,
其中乙规格比甲规格每套贵20元.
(1)若用700元购买甲规格与用900元购买乙规格的数量相同,求甲、乙两种规格每套吉祥物的价格;
(2)在(1)的条件下,若购买甲规格数量不超过乙规格数量的2倍,如何购买才能使总费用最少?
23.如图1,公园草坪的地面O处有一根直立水管,喷水口可上下移动,喷出的抛物线形水线也随之上下平移,图2是其示意图.开始喷水后,若喷水口在O处,水线落地点为A,若喷水口上升到P处,水线落地点为B,记长度为h.
(1)已知.若喷水口在P处,,.
①求水线最高点与点B之间的水平距离;
②求水线的最大高度;
③身高的小红要从水线下某点经过,为了不被水喷到,该点与O的水平距离应满足什么条件?请说明理由.
(2)在喷水口上升过程中,当时,用含h的式子表示水线的最大高度.
24.如图1,已知为的直径,弦于点,是上一点,连接,,.
(1)求证:;
(2)如图2,延长相交于点,连接.
①已知,求的长;
②记与的交点为,若,当时,求的值.
2024年浙江省中考数学模拟练习试卷(解析版)
(考试时间:120分钟 试卷满分:120分)
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下图是由一个长方体和一个圆柱组成的几何体,它的俯视图是( )
A. B. C. D.
【答案】D
【解析】
【分析】根据从上面看得到的图形是俯视图即可解答.
【详解】解:从上面看下边是一个矩形,矩形的上边是一个圆,
故选:D.
2.下列计算正确的是( )
A. B. C. D.
【答案】C
【分析】根据整式的减法运算,同底数幂的乘法、除法运算,幂的乘方进行运算求解,然后进行判断即可.
【详解】解:A中,错误,故不符合要求;
B中,错误,故不符合要求;
C中,正确,故符合要求;
D中,错误,故不符合要求;
故选C.
截至2022年3月24日,携带“祝融号”火星车的“天问一号”环绕器在轨运行609天,
距离地球277000000千米;数据277000000用科学记数法表示为( )
A. B. C. D.
【答案】D
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.
确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同,
当原数绝对值≥10时,n是正整数数.
【详解】解:由题意可知:
.
故选:D.
4.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
【答案】C
【分析】中心对称是指把一个图形绕着某一点旋转,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,中心对称,是针对两个图形而言,是指两个图形的(位置)关系;如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.由此即可求解.
【详解】解:A选项,不是轴对称图形,也不是中心对称图形,不符合题意;
B选项,不是轴对称图形,是中心对称图形,不符合题意;
C选项,是轴对称图形,也是中心对称图形,符合题意;
D选项,是轴对称图形,不是中心对称图形,不符合题意;
故选:C.
5.已知点P(m﹣3,m﹣1)在第二象限,则m的取值范围在数轴上表示正确的是( )
A. B.
C. D.
【答案】D
【分析】先根据题意列出不等式组,求出其中各不等式的解集,再求出这些解集的公共部分即可.
【详解】解:∵点P(m﹣3,m﹣1)在第二象限,
∴,
解得:1<m<3,
故选D.
6.化简的结果是( )
A. B. C. D.
【答案】A
【分析】根据题意首先应通分,然后进行分式的加减运算进而上下约分即可得出答案.
【详解】解:
故选:A.
7 .从甲、乙、丙三人中任选两人参加青年志愿者活动,甲被选中的概率是( )
A. B. C. D.
【答案】C
【分析】画出树状图,共有6种等可能的结果,其中甲被选中的结果有4种,由概率公式即可得出结果.
【详解】解:根据题意画图如下:
共有6种等可能的结果数,其中甲被选中的结果有4种,
则甲被选中的概率为.
故选:C.
8. 如图,为的直径,C、D为上的点,,若,则( )
A. B. C. D.
【答案】D
【分析】连接 、,如图,利用等腰三角形的性质和三角形内角和定理计算出 ,再根据圆心角、弧、弦的关系得到 ,然后根据圆周角定理得到 的度数;
【详解】连接 、,如图,
故选:D
9.如图,在平面直角坐标系xOy中,直线AB经过A(4,0)、B(0,4),⊙O的半径为2(O为坐标原点),点P是直线AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
A. B.2 ﹣1 C.2 D.3
【答案】C
【分析】连接OP、OQ,根据勾股定理知 当PO⊥AB时,线段PQ最短,即线段PQ最小.
【详解】解:如图,连接OP、OQ.
∵PQ是⊙O的切线,
∴OQ⊥PQ;
由勾股定理知,
∵当PO⊥AB时,线段PQ最短;
又∵A(4,0)、B(0,4),
∴OA=OB=4,
∴,
∴,
∵OQ=2,
∴.
故选C.
10.如图,矩形的内部有5个全等的小正方形,小正方形的顶点分别落在边上,若,则小正方形的边长为( )
A. B.5 C. D.
【答案】B
【分析】由矩形的性质可得,求出,证得,得出,过点K作于K,可证明,利用相似三角形对应边成比例求出,再求出,然后利用勾股定理列式求出EG,然后求解即可.
【详解】解:∵四边形是矩形,
∴,
∴,
∴,
∵5个小正方形全等,
∴,
在和中,,
∴,
∴,
过点K作于K,如下图所示,
则四边形为矩形,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
在中,,
∴小正方形的边长为,
故选:B.
二、填空题:本题共6小题,每小题3分,共18分。
11..因式分解: .
【答案】
【分析】先提取公因式3,再利用平方差公式分解可得结果
【详解】原式=
=.
故答案为:
12.如图,用一个半径为10cm的定滑轮带动重物上升,滑轮上一点P旋转了36°,
假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了__________
【答案】2πcm
【分析】根据定滑轮的性质得到重物上升的高度即为滑轮转过的弧长,利用弧长公式计算即可.
【详解】解:根据题意得:滑轮转过的弧长
则重物上升了2πcm,
故答案为:2πcm
若购买荔枝所付金额y(元)与购买数量x(千克)之间的函数图像如图所示,
则购买3千克荔枝需要付 元.
【答案】
【分析】根据图像可得购买3kg荔枝需要付的钱即为当x=3时,y所对应的值,即求出AB段的函数解析式,将x=3代入即可.
【详解】解:设直线的解析式为:,
由图像可知:,
∴,
∴,
当时,,
故答案为:.
如图,是的切线,交于点,,连接,,
若,则的度数为 .
【答案】
【分析】本题考查了切线的性质,等腰三角形的性质以及三角形内角和定理的应用;连接,根据切线的性质可得,根据已知条件可得,进而根据等腰三角形的性质以及三角形内角和定理,可得,进而即可求解.
【详解】解:连接,
∵,是的切线,
∴,
又∵,
∴,
∵,
∴,
∴,
故答案为:.
如图,在正方形ABCD中,点E是边BC上的一点,点F在边CD的延长线上,且,
连接EF交边AD于点G.过点A作,垂足为点M,交边CD于点N.
若,,则线段AN的长为
【答案】
【分析】连接AE、AF、EN,首先可证得,AE=AF,可证得垂直平分EF,可得EN=FN,再根据勾股定理即可求得正方形的边长,再根据勾股定理即可求得AN的长.
【详解】解:如图:连接AE、AF、EN,
四边形ABCD是正方形
设AB=BC=CD=AD=a,,
在与中,
,
,
是等腰三角形,
又,
垂直平分EF,
,
又,
,
在中,,
,
解得a=20,
,,
在中,,
,
故答案为:.
16.如图,在矩形和正方形中,点A在y轴正半轴上,点C,F均在x轴正半轴上,
点D在边上,,.若点B,E在同一个反比例函数的图象上,
则这个反比例函数的表达式是__________.
【答案】
【解析】
【分析】设正方形的边长为m,根据,,得到,根据矩形对边相等得到,推出,根据点B,E在同一个反比例函数的图象上,得到,得到,推出.
【详解】解:∵四边形是矩形,
∴,
设正方形的边长为m,
∴,
∵,
∴,
∴,,
设反比例函数的表达式为,
∴,
解得或(不合题意,舍去),
∴,
∴,
∴这个反比例函数的表达式是,
故答案为:.
三、解答题(第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.(1).
(2).
【答案】(1);(2)
【分析】(1)先计算负整数指数、0指数幂、化简二次根式和绝对值,再计算加减即可;
(2)根据同分母分式的加减法则解答即可.
【详解】解:(1)
.
(2)
.
如图,在的网格中,线段的端点都在格点上(两条网格线的交点叫格点).
请用无刻度的直尺画出符合要求的图形,并保留画图痕迹(不要求写画法).
(1)在图1中画出一个以为边的,使顶点在格点上.
(2)在图2中的线段上找出一点,使.
【答案】(1)答案见解析
(2)答案见解析
【分析】(1)取格点C,连接和即可;
(2)取格点E,F,连接交于点D,点D即为所求.
【详解】(1)解:如下图,取格点C,连接和,
由题意可知:,
为;
(2)如下图,取格点E,F,连接交于点D,
由题意可知:,
,
,
点D即为所求.
19.“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
【答案】(1)600;(2)见解析;(3)3200;(4)
【详解】(1)60÷10%=600(人).
答:本次参加抽样调查的居民有600人.
(2)如图,
(3)8000×40%=3200(人).
答:该居民区有8000人,估计爱吃D粽的人有3200人.
(4)如图;
共有12种等可能的情况,其中他第二个吃到的恰好是C粽的有3种,
∴P(C粽)==.
答:他第二个吃到的恰好是C粽的概率是.
图1是一台手机支架,图2是其侧面示意图,,可分别绕点A,B转动,
测得,,,.
(1)在图2中,过点B作,垂足为E.填空:______°;______cm(结果保留根号);
(2)在(1)的条件下,求点C到的距离.
(结果保留一位小数,参考数据:,,,)
【答案】(1),
(2)
【分析】(1)根据垂直定义可得,从而利用直角三角形的两个锐角互余可得,然后利用角的和差关系进行计算即可得;再解即可求出的长;
(2)过点C作,垂足为F,过点C作,垂足为G,则,,从而利用直角三角形的两个锐角互余可得,在中,利用锐角三角函数的定义求出的长,进行计算即可解答.
【详解】(1)如图:
∵,
∴,
∵,
∴,
∵,
∴;
在中,,
∴,
故答案为:20;
(2)过点C作,垂足为F,过点C作,垂足为G,
则,,
在中,,
∵,
∴,
∴,
∴点C到AD的距离为.
已知:如图,在平行四边形中, 的平分线交于点E,点F是的中点,
连接并延长交于点G,连接.
(1)求证:四边形是菱形;
(2)若,,求的长.
【答案】(1)见解析
(2)
【分析】(1)先证明,然后证明,得,
证出四边形是平行四边形,即可得出结论;
(2)过点F作于点M,由菱形的性质得出,,在中,求出,在中,求出,再求出,得出,中,由勾股定理即可得出的长.
【详解】(1)证明:∵平分,
∴,
∵四边形是平行四边形,
∴且,
∴,
∴,
∴,
∵点F是的中点,
∴,
∵,
∴,
∴,
∵,
∴四边形AEGB是平行四边形,
∵,
∴四边形是菱形;
(2)解:∵,
∴,
过点F作于点M,如图所示:
∵四边形是菱形,
∴,
∴,
∴,
∴,
∴,
∴,
在中,根据勾股定理得:
.
22.第19届杭州亚运会,吉祥物为“宸宸”、“琮琮”、“莲莲”,
如图,某校准备举行“第19届亚运会”知识竞赛活动,
拟购买30套吉祥物(“宸宸”、“琮琮”、“莲莲”)作为竞赛奖品.某商店有甲,乙两种规格,
其中乙规格比甲规格每套贵20元.
(1)若用700元购买甲规格与用900元购买乙规格的数量相同,求甲、乙两种规格每套吉祥物的价格;
(2)在(1)的条件下,若购买甲规格数量不超过乙规格数量的2倍,如何购买才能使总费用最少?
(1)解:设甲规格吉祥物每套价格元,则乙规格每套价格为元,
根据题意,得,
解得.
经检验,是所列方程的根,且符合实际意义.
.
答:甲规格吉祥物每套价格为70元,乙规格每套为90元.
(2)解:设乙规格购买套,甲规格购买套,总费用为元
根据题意,得
,
解得,
,
,
随的增大而增大.
当时,最小值.
故乙规格购买10套、甲规格购买20套总费用最少.
23.如图1,公园草坪的地面O处有一根直立水管,喷水口可上下移动,喷出的抛物线形水线也随之上下平移,图2是其示意图.开始喷水后,若喷水口在O处,水线落地点为A,若喷水口上升到P处,水线落地点为B,记长度为h.
(1)已知.若喷水口在P处,,.
①求水线最高点与点B之间的水平距离;
②求水线的最大高度;
③身高的小红要从水线下某点经过,为了不被水喷到,该点与O的水平距离应满足什么条件?请说明理由.
(2)在喷水口上升过程中,当时,用含h的式子表示水线的最大高度.
【答案】(1)①水线最高点与点B之间的水平距离为2米;②水线的最大高度为米;③该点与O的水平距离应小于4米
(2)水线的最大高度是米
【分析】本题考查了二次函数的实际应用,解题的关键是正确理解题意,熟练掌握用待定系数法求解函数解析式的方法和步骤,以及二次函数的性质.
(1)①根据得出抛物线对称轴为直线,即可解答;②根据抛物线对称轴为直线,得出,得出,设,把代入得求出a、b、c的值,进而得出该抛物线的解析式,即可解答;③把代入,求出函数值,结合二次函数的增减性,即可解答;
(2)设,则,则抛物线对称轴为直线,,设该抛物线解析式为. ,代入得,推出,即可解答.
【详解】(1)解:①∵,
∴抛物线对称轴为直线,
∴水线最高点与点B之间的水平距离为2米;
②∵抛物线对称轴为直线,
∴,
整理得:,
∵,,
∴,
设,
把代入得:
,
解得:,
∴该抛物线的解析式为,
∵,,
∴当时,y取最大值,
∴水线的最大高度为米;
③把代入得:,
解得:,
∵,抛物线对称轴为直线,
∴当时,y随x的增大而增大,当时,y随x的增大而减小,
∴,
∴该点与O的水平距离应小于4米;
(2)解:设,则,
∴抛物线对称轴为直线,,
∴,
设该抛物线解析式为.
∵,
∴,
设,
把,代入得:
,
得:,
∴,
∴水线的最大高度是米.
24.如图1,已知为的直径,弦于点,是上一点,连接,,.
(1)求证:;
(2)如图2,延长相交于点,连接.
①已知,求的长;
②记与的交点为,若,当时,求的值.
【答案】(1)见解析
(2)①;②
【分析】(1)根据垂径定理得出,再根据圆周角定理即可得出答案;
(2)①证明,得出,代入数据求出结果即可;
②连接,根据垂径定理得出,根据勾股定理得出,根据等腰三角形的性质得出,平分,证明,得出即可.
【详解】(1)证明:是直径,,
,
.
(2)解:①,,
∴,
,
,
.
②连接,
是直径,,
,
,
,
,
,
,
,
,
又,
,平分,
,,
,
四边形是圆的内接四边形,
,,
由(1)可知,
,
∴,
.
(考试时间:120分钟 试卷满分:120分)
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下图是由一个长方体和一个圆柱组成的几何体,它的俯视图是( )
A. B. C. D.
2.下列计算正确的是( )
A. B. C. D.
截至2022年3月24日,携带“祝融号”火星车的“天问一号”环绕器在轨运行609天,
距离地球277000000千米;数据277000000用科学记数法表示为( )
A. B. C. D.
4.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
5.已知点P(m﹣3,m﹣1)在第二象限,则m的取值范围在数轴上表示正确的是( )
A. B.
C. D.
6.化简的结果是( )
A. B. C. D.
7 .从甲、乙、丙三人中任选两人参加青年志愿者活动,甲被选中的概率是( )
A. B. C. D.
8. 如图,为的直径,C、D为上的点,,若,则( )
A. B. C. D.
9.如图,在平面直角坐标系xOy中,直线AB经过A(4,0)、B(0,4),⊙O的半径为2(O为坐标原点),点P是直线AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
A. B.2 ﹣1 C.2 D.3
10.如图,矩形的内部有5个全等的小正方形,小正方形的顶点分别落在边上,若,则小正方形的边长为( )
A. B.5 C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11..因式分解: .
12.如图,用一个半径为10cm的定滑轮带动重物上升,滑轮上一点P旋转了36°,
假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了__________
若购买荔枝所付金额y(元)与购买数量x(千克)之间的函数图像如图所示,
则购买3千克荔枝需要付 元.
如图,是的切线,交于点,,连接,,
若,则的度数为 .
如图,在正方形ABCD中,点E是边BC上的一点,点F在边CD的延长线上,且,
连接EF交边AD于点G.过点A作,垂足为点M,交边CD于点N.
若,,则线段AN的长为
16.如图,在矩形和正方形中,点A在y轴正半轴上,点C,F均在x轴正半轴上,
点D在边上,,.若点B,E在同一个反比例函数的图象上,
则这个反比例函数的表达式是__________.
三、解答题(第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.(1).
(2).
如图,在的网格中,线段的端点都在格点上(两条网格线的交点叫格点).
请用无刻度的直尺画出符合要求的图形,并保留画图痕迹(不要求写画法).
(1)在图1中画出一个以为边的,使顶点在格点上.
(2)在图2中的线段上找出一点,使.
19.“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
图1是一台手机支架,图2是其侧面示意图,,可分别绕点A,B转动,
测得,,,.
(1)在图2中,过点B作,垂足为E.填空:______°;______cm(结果保留根号);
(2)在(1)的条件下,求点C到的距离.
(结果保留一位小数,参考数据:,,,)
已知:如图,在平行四边形中, 的平分线交于点E,点F是的中点,
连接并延长交于点G,连接.
(1)求证:四边形是菱形;
(2)若,,求的长.
22.第19届杭州亚运会,吉祥物为“宸宸”、“琮琮”、“莲莲”,
如图,某校准备举行“第19届亚运会”知识竞赛活动,
拟购买30套吉祥物(“宸宸”、“琮琮”、“莲莲”)作为竞赛奖品.某商店有甲,乙两种规格,
其中乙规格比甲规格每套贵20元.
(1)若用700元购买甲规格与用900元购买乙规格的数量相同,求甲、乙两种规格每套吉祥物的价格;
(2)在(1)的条件下,若购买甲规格数量不超过乙规格数量的2倍,如何购买才能使总费用最少?
23.如图1,公园草坪的地面O处有一根直立水管,喷水口可上下移动,喷出的抛物线形水线也随之上下平移,图2是其示意图.开始喷水后,若喷水口在O处,水线落地点为A,若喷水口上升到P处,水线落地点为B,记长度为h.
(1)已知.若喷水口在P处,,.
①求水线最高点与点B之间的水平距离;
②求水线的最大高度;
③身高的小红要从水线下某点经过,为了不被水喷到,该点与O的水平距离应满足什么条件?请说明理由.
(2)在喷水口上升过程中,当时,用含h的式子表示水线的最大高度.
24.如图1,已知为的直径,弦于点,是上一点,连接,,.
(1)求证:;
(2)如图2,延长相交于点,连接.
①已知,求的长;
②记与的交点为,若,当时,求的值.
2024年浙江省中考数学模拟练习试卷(解析版)
(考试时间:120分钟 试卷满分:120分)
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下图是由一个长方体和一个圆柱组成的几何体,它的俯视图是( )
A. B. C. D.
【答案】D
【解析】
【分析】根据从上面看得到的图形是俯视图即可解答.
【详解】解:从上面看下边是一个矩形,矩形的上边是一个圆,
故选:D.
2.下列计算正确的是( )
A. B. C. D.
【答案】C
【分析】根据整式的减法运算,同底数幂的乘法、除法运算,幂的乘方进行运算求解,然后进行判断即可.
【详解】解:A中,错误,故不符合要求;
B中,错误,故不符合要求;
C中,正确,故符合要求;
D中,错误,故不符合要求;
故选C.
截至2022年3月24日,携带“祝融号”火星车的“天问一号”环绕器在轨运行609天,
距离地球277000000千米;数据277000000用科学记数法表示为( )
A. B. C. D.
【答案】D
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.
确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同,
当原数绝对值≥10时,n是正整数数.
【详解】解:由题意可知:
.
故选:D.
4.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
【答案】C
【分析】中心对称是指把一个图形绕着某一点旋转,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,中心对称,是针对两个图形而言,是指两个图形的(位置)关系;如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.由此即可求解.
【详解】解:A选项,不是轴对称图形,也不是中心对称图形,不符合题意;
B选项,不是轴对称图形,是中心对称图形,不符合题意;
C选项,是轴对称图形,也是中心对称图形,符合题意;
D选项,是轴对称图形,不是中心对称图形,不符合题意;
故选:C.
5.已知点P(m﹣3,m﹣1)在第二象限,则m的取值范围在数轴上表示正确的是( )
A. B.
C. D.
【答案】D
【分析】先根据题意列出不等式组,求出其中各不等式的解集,再求出这些解集的公共部分即可.
【详解】解:∵点P(m﹣3,m﹣1)在第二象限,
∴,
解得:1<m<3,
故选D.
6.化简的结果是( )
A. B. C. D.
【答案】A
【分析】根据题意首先应通分,然后进行分式的加减运算进而上下约分即可得出答案.
【详解】解:
故选:A.
7 .从甲、乙、丙三人中任选两人参加青年志愿者活动,甲被选中的概率是( )
A. B. C. D.
【答案】C
【分析】画出树状图,共有6种等可能的结果,其中甲被选中的结果有4种,由概率公式即可得出结果.
【详解】解:根据题意画图如下:
共有6种等可能的结果数,其中甲被选中的结果有4种,
则甲被选中的概率为.
故选:C.
8. 如图,为的直径,C、D为上的点,,若,则( )
A. B. C. D.
【答案】D
【分析】连接 、,如图,利用等腰三角形的性质和三角形内角和定理计算出 ,再根据圆心角、弧、弦的关系得到 ,然后根据圆周角定理得到 的度数;
【详解】连接 、,如图,
故选:D
9.如图,在平面直角坐标系xOy中,直线AB经过A(4,0)、B(0,4),⊙O的半径为2(O为坐标原点),点P是直线AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
A. B.2 ﹣1 C.2 D.3
【答案】C
【分析】连接OP、OQ,根据勾股定理知 当PO⊥AB时,线段PQ最短,即线段PQ最小.
【详解】解:如图,连接OP、OQ.
∵PQ是⊙O的切线,
∴OQ⊥PQ;
由勾股定理知,
∵当PO⊥AB时,线段PQ最短;
又∵A(4,0)、B(0,4),
∴OA=OB=4,
∴,
∴,
∵OQ=2,
∴.
故选C.
10.如图,矩形的内部有5个全等的小正方形,小正方形的顶点分别落在边上,若,则小正方形的边长为( )
A. B.5 C. D.
【答案】B
【分析】由矩形的性质可得,求出,证得,得出,过点K作于K,可证明,利用相似三角形对应边成比例求出,再求出,然后利用勾股定理列式求出EG,然后求解即可.
【详解】解:∵四边形是矩形,
∴,
∴,
∴,
∵5个小正方形全等,
∴,
在和中,,
∴,
∴,
过点K作于K,如下图所示,
则四边形为矩形,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
在中,,
∴小正方形的边长为,
故选:B.
二、填空题:本题共6小题,每小题3分,共18分。
11..因式分解: .
【答案】
【分析】先提取公因式3,再利用平方差公式分解可得结果
【详解】原式=
=.
故答案为:
12.如图,用一个半径为10cm的定滑轮带动重物上升,滑轮上一点P旋转了36°,
假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了__________
【答案】2πcm
【分析】根据定滑轮的性质得到重物上升的高度即为滑轮转过的弧长,利用弧长公式计算即可.
【详解】解:根据题意得:滑轮转过的弧长
则重物上升了2πcm,
故答案为:2πcm
若购买荔枝所付金额y(元)与购买数量x(千克)之间的函数图像如图所示,
则购买3千克荔枝需要付 元.
【答案】
【分析】根据图像可得购买3kg荔枝需要付的钱即为当x=3时,y所对应的值,即求出AB段的函数解析式,将x=3代入即可.
【详解】解:设直线的解析式为:,
由图像可知:,
∴,
∴,
当时,,
故答案为:.
如图,是的切线,交于点,,连接,,
若,则的度数为 .
【答案】
【分析】本题考查了切线的性质,等腰三角形的性质以及三角形内角和定理的应用;连接,根据切线的性质可得,根据已知条件可得,进而根据等腰三角形的性质以及三角形内角和定理,可得,进而即可求解.
【详解】解:连接,
∵,是的切线,
∴,
又∵,
∴,
∵,
∴,
∴,
故答案为:.
如图,在正方形ABCD中,点E是边BC上的一点,点F在边CD的延长线上,且,
连接EF交边AD于点G.过点A作,垂足为点M,交边CD于点N.
若,,则线段AN的长为
【答案】
【分析】连接AE、AF、EN,首先可证得,AE=AF,可证得垂直平分EF,可得EN=FN,再根据勾股定理即可求得正方形的边长,再根据勾股定理即可求得AN的长.
【详解】解:如图:连接AE、AF、EN,
四边形ABCD是正方形
设AB=BC=CD=AD=a,,
在与中,
,
,
是等腰三角形,
又,
垂直平分EF,
,
又,
,
在中,,
,
解得a=20,
,,
在中,,
,
故答案为:.
16.如图,在矩形和正方形中,点A在y轴正半轴上,点C,F均在x轴正半轴上,
点D在边上,,.若点B,E在同一个反比例函数的图象上,
则这个反比例函数的表达式是__________.
【答案】
【解析】
【分析】设正方形的边长为m,根据,,得到,根据矩形对边相等得到,推出,根据点B,E在同一个反比例函数的图象上,得到,得到,推出.
【详解】解:∵四边形是矩形,
∴,
设正方形的边长为m,
∴,
∵,
∴,
∴,,
设反比例函数的表达式为,
∴,
解得或(不合题意,舍去),
∴,
∴,
∴这个反比例函数的表达式是,
故答案为:.
三、解答题(第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.(1).
(2).
【答案】(1);(2)
【分析】(1)先计算负整数指数、0指数幂、化简二次根式和绝对值,再计算加减即可;
(2)根据同分母分式的加减法则解答即可.
【详解】解:(1)
.
(2)
.
如图,在的网格中,线段的端点都在格点上(两条网格线的交点叫格点).
请用无刻度的直尺画出符合要求的图形,并保留画图痕迹(不要求写画法).
(1)在图1中画出一个以为边的,使顶点在格点上.
(2)在图2中的线段上找出一点,使.
【答案】(1)答案见解析
(2)答案见解析
【分析】(1)取格点C,连接和即可;
(2)取格点E,F,连接交于点D,点D即为所求.
【详解】(1)解:如下图,取格点C,连接和,
由题意可知:,
为;
(2)如下图,取格点E,F,连接交于点D,
由题意可知:,
,
,
点D即为所求.
19.“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
【答案】(1)600;(2)见解析;(3)3200;(4)
【详解】(1)60÷10%=600(人).
答:本次参加抽样调查的居民有600人.
(2)如图,
(3)8000×40%=3200(人).
答:该居民区有8000人,估计爱吃D粽的人有3200人.
(4)如图;
共有12种等可能的情况,其中他第二个吃到的恰好是C粽的有3种,
∴P(C粽)==.
答:他第二个吃到的恰好是C粽的概率是.
图1是一台手机支架,图2是其侧面示意图,,可分别绕点A,B转动,
测得,,,.
(1)在图2中,过点B作,垂足为E.填空:______°;______cm(结果保留根号);
(2)在(1)的条件下,求点C到的距离.
(结果保留一位小数,参考数据:,,,)
【答案】(1),
(2)
【分析】(1)根据垂直定义可得,从而利用直角三角形的两个锐角互余可得,然后利用角的和差关系进行计算即可得;再解即可求出的长;
(2)过点C作,垂足为F,过点C作,垂足为G,则,,从而利用直角三角形的两个锐角互余可得,在中,利用锐角三角函数的定义求出的长,进行计算即可解答.
【详解】(1)如图:
∵,
∴,
∵,
∴,
∵,
∴;
在中,,
∴,
故答案为:20;
(2)过点C作,垂足为F,过点C作,垂足为G,
则,,
在中,,
∵,
∴,
∴,
∴点C到AD的距离为.
已知:如图,在平行四边形中, 的平分线交于点E,点F是的中点,
连接并延长交于点G,连接.
(1)求证:四边形是菱形;
(2)若,,求的长.
【答案】(1)见解析
(2)
【分析】(1)先证明,然后证明,得,
证出四边形是平行四边形,即可得出结论;
(2)过点F作于点M,由菱形的性质得出,,在中,求出,在中,求出,再求出,得出,中,由勾股定理即可得出的长.
【详解】(1)证明:∵平分,
∴,
∵四边形是平行四边形,
∴且,
∴,
∴,
∴,
∵点F是的中点,
∴,
∵,
∴,
∴,
∵,
∴四边形AEGB是平行四边形,
∵,
∴四边形是菱形;
(2)解:∵,
∴,
过点F作于点M,如图所示:
∵四边形是菱形,
∴,
∴,
∴,
∴,
∴,
∴,
在中,根据勾股定理得:
.
22.第19届杭州亚运会,吉祥物为“宸宸”、“琮琮”、“莲莲”,
如图,某校准备举行“第19届亚运会”知识竞赛活动,
拟购买30套吉祥物(“宸宸”、“琮琮”、“莲莲”)作为竞赛奖品.某商店有甲,乙两种规格,
其中乙规格比甲规格每套贵20元.
(1)若用700元购买甲规格与用900元购买乙规格的数量相同,求甲、乙两种规格每套吉祥物的价格;
(2)在(1)的条件下,若购买甲规格数量不超过乙规格数量的2倍,如何购买才能使总费用最少?
(1)解:设甲规格吉祥物每套价格元,则乙规格每套价格为元,
根据题意,得,
解得.
经检验,是所列方程的根,且符合实际意义.
.
答:甲规格吉祥物每套价格为70元,乙规格每套为90元.
(2)解:设乙规格购买套,甲规格购买套,总费用为元
根据题意,得
,
解得,
,
,
随的增大而增大.
当时,最小值.
故乙规格购买10套、甲规格购买20套总费用最少.
23.如图1,公园草坪的地面O处有一根直立水管,喷水口可上下移动,喷出的抛物线形水线也随之上下平移,图2是其示意图.开始喷水后,若喷水口在O处,水线落地点为A,若喷水口上升到P处,水线落地点为B,记长度为h.
(1)已知.若喷水口在P处,,.
①求水线最高点与点B之间的水平距离;
②求水线的最大高度;
③身高的小红要从水线下某点经过,为了不被水喷到,该点与O的水平距离应满足什么条件?请说明理由.
(2)在喷水口上升过程中,当时,用含h的式子表示水线的最大高度.
【答案】(1)①水线最高点与点B之间的水平距离为2米;②水线的最大高度为米;③该点与O的水平距离应小于4米
(2)水线的最大高度是米
【分析】本题考查了二次函数的实际应用,解题的关键是正确理解题意,熟练掌握用待定系数法求解函数解析式的方法和步骤,以及二次函数的性质.
(1)①根据得出抛物线对称轴为直线,即可解答;②根据抛物线对称轴为直线,得出,得出,设,把代入得求出a、b、c的值,进而得出该抛物线的解析式,即可解答;③把代入,求出函数值,结合二次函数的增减性,即可解答;
(2)设,则,则抛物线对称轴为直线,,设该抛物线解析式为. ,代入得,推出,即可解答.
【详解】(1)解:①∵,
∴抛物线对称轴为直线,
∴水线最高点与点B之间的水平距离为2米;
②∵抛物线对称轴为直线,
∴,
整理得:,
∵,,
∴,
设,
把代入得:
,
解得:,
∴该抛物线的解析式为,
∵,,
∴当时,y取最大值,
∴水线的最大高度为米;
③把代入得:,
解得:,
∵,抛物线对称轴为直线,
∴当时,y随x的增大而增大,当时,y随x的增大而减小,
∴,
∴该点与O的水平距离应小于4米;
(2)解:设,则,
∴抛物线对称轴为直线,,
∴,
设该抛物线解析式为.
∵,
∴,
设,
把,代入得:
,
得:,
∴,
∴水线的最大高度是米.
24.如图1,已知为的直径,弦于点,是上一点,连接,,.
(1)求证:;
(2)如图2,延长相交于点,连接.
①已知,求的长;
②记与的交点为,若,当时,求的值.
【答案】(1)见解析
(2)①;②
【分析】(1)根据垂径定理得出,再根据圆周角定理即可得出答案;
(2)①证明,得出,代入数据求出结果即可;
②连接,根据垂径定理得出,根据勾股定理得出,根据等腰三角形的性质得出,平分,证明,得出即可.
【详解】(1)证明:是直径,,
,
.
(2)解:①,,
∴,
,
,
.
②连接,
是直径,,
,
,
,
,
,
,
,
,
又,
,平分,
,,
,
四边形是圆的内接四边形,
,,
由(1)可知,
,
∴,
.
同课章节目录
