勾股定理证明教学设计

勾 股 定 理
允山中学 郑毅
一、教学目标
1. 知识与技能：①、探索、发现并掌握勾股定理及其证明。
②、会运用勾股定理进行简单的计算和实际应用。
2. 过程与方法：在探索勾股定理的过程中，让学生经历 “观察—猜想—归纳—验证”的数学思维。
3. 情感态度与价值观：形成实事求是的科学态度以及质疑和独立思考的习惯.
二、教学重点、难点
1．重点：通过拼图探索勾股定理
2．难点：利用数形结合的方法证明勾股定理,形成数形结合的意识。
三、教学过程
（一）、新课引入
电线杆长6米，杆底部距离钢丝绳底部2.5米，你有办法确定钢丝绳的长度吗？
（二）、探究定理
1、做一做
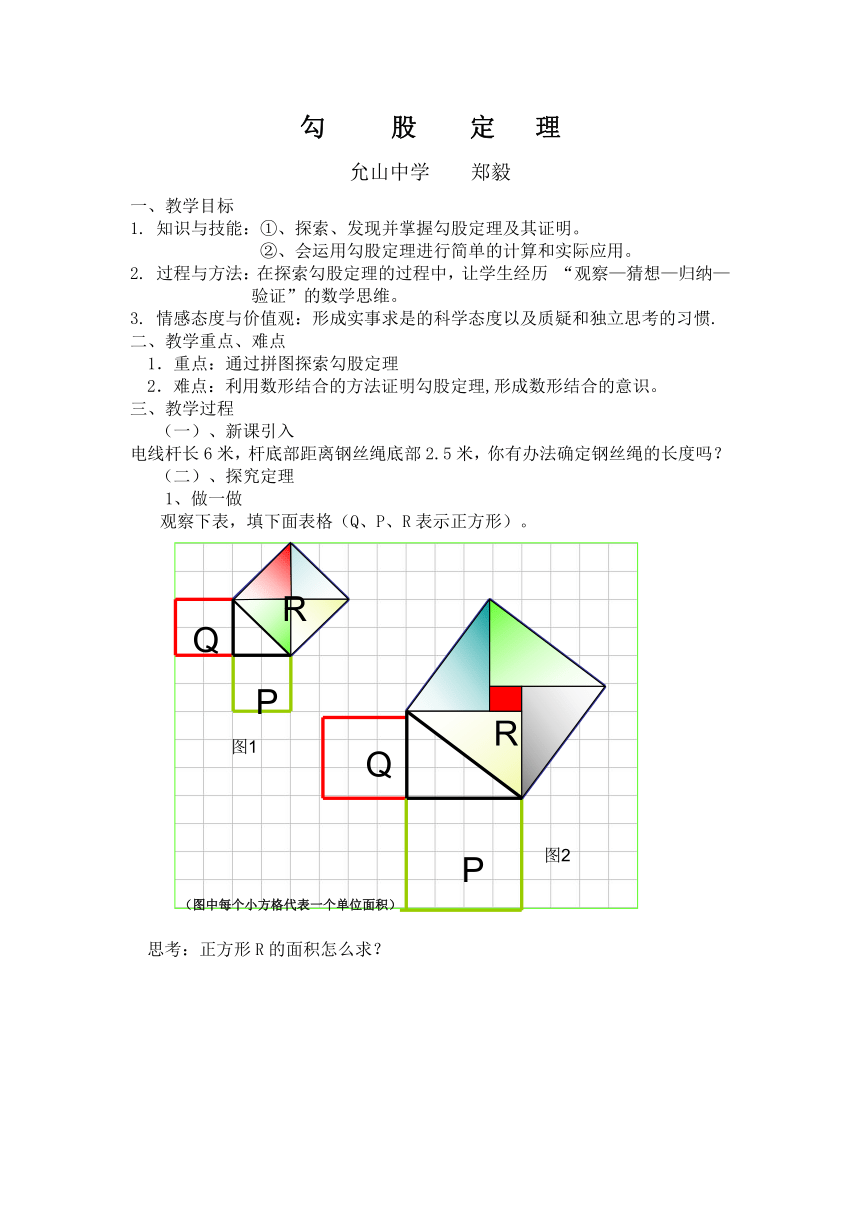
观察下表，填下面表格（Q、P、R表示正方形）。
思考：正方形R的面积怎么求？
问题①：两个小正方形P、Q的面积与大正方形R的面积有何关系？
问题②：如果我们把三个正方形与它围成的直角三角形ABC联系起来看，则上述关系可以怎样表示呢？
2、议一议
对于其他的直角三角形也有这个性质吗？
3、猜一猜
直角三角形的两直角边的平方和等于斜边的平方。即在△ABC中，∠C=90°，∠A、∠B、∠C的对边为a、b、c，有 a2＋b2=c2
4、探一探（小组活动,四人一组）
⑴、请同学们拿出准备好的4个全等的直角三角形模型，三边分别标好a,b,c（a【小组合作探究】，思考：
问题1：你有几种拼法？
问题2：图中分别有几个正方形？几个直角三角形？
问题3：大正方形由哪几个图形构成？
问题4：它们的面积之间满足什么样的关系？
问题5：分别怎么来表示它们的面积？
⑵、证明：
5、归纳总结
勾股定理：直角三角形两直角边的平方和等于斜边的平方。即在△ABC中，∠C=90°，∠A、∠B、∠C的对边为a、b、c，有a2＋b2=c2。
公式变形：
我国称这个结论为“勾股定理”，西方称它为“毕达哥拉斯定理”，为什么呢？
（1）介绍《周髀算经》中西周的商高（公元一千多年前）发现了勾三股四弦五 这个规律
（2）介绍西方毕达哥拉斯于公元前582～493时期发现了勾股定理；
（三）、勾股定理的应用
例：求出下列直角三角形中未知边的长度。
（四）解决问题：
电线杆长6米，杆底部距离钢丝绳底部2.5米，你有办法确定钢丝绳的长度吗？
A
6米
　　　　　　　　　　　　　　　　　　　　　　　　　　　Ｃ　米　Ｂ
你能又快又准确吗？
1、在Rt△ABC中，∠C=90°
（1）若a=5,b=12,则c=
（2）若b=15，c=25，则a=
（3）若a：b=3：4，c=10，则a= b=
2、求下图中未知数x、y的值
3、直角三角形有两条边长度分别为3和4，求第三边长为。
4、在一直角三角形中,两直角边分别为3和4,求斜边上的高。
（五）小结： 　　　　　　　　　
1、本节课我们经历了怎样的过程？ 　　　　　　　　　　　　　　
2、本节课我们学到了什么？
3、学了本节课后我们有什么感想？
（六）拓展练习：
如图6，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形G的边长为7cm,则正方形A，B，C，D的面积之和为_________cm2。
（七）作业：
1、教科书第16页A 1、3、4
2、查资料找勾股定理其他证法。
Q
P
Q
P
图1
图2
（图中每个小方格代表一个单位面积）
R
R
图2
图1
R的面积
（单位面积）
P的面积
（单位面积）
Q的面积
（单位面积）
b
b
b
b
c
c
c
c
a
a
a
a
图2
c2=a2 + b2
a2=c2－b2
b2 =c2-a2
9
12
x
x
5
13
A
C
B