第六单元 圆 单元复习卷 苏教版五年级数学下册(含解析)
文档属性
| 名称 | 第六单元 圆 单元复习卷 苏教版五年级数学下册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 188.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 14:28:24 | ||
图片预览



文档简介
第六单元 圆 单元复习卷 苏教版五年级数学下册
一、单选题
1.在一个钟面上,分针长8cm,时针长6cm,从下午3时到下午4时,分针扫过的面积是( )cm2。
A.200.96 B.113.04 C.50.24 D.28.26
2.车轮转动一周的路程就是车轮的( )
A.周长 B.直径 C.半径 D.面积
3.将圆剪拼成一个长方形,这个长方形的长等于( )
A.r B.πr C.2πr D.πr2
4.下列四个图案中,哪个图案的阴影部分面积与其他三个不同( )
A. B.
C. D.
5.一个半圆的半径是3厘米,它的周长是( )厘米。
A.18.84 B.9.42 C.12.42 D.15.42
6.下列说法中正确的是( )
A.圆周率就是3.14。
B.由于圆的位置不同,所以圆的周长不同。
C.直径是圆内最长的线段。
D.直径是线段,半径是射线。
7.小聪骑自行车到学校用10分钟,从小聪家到学校大约多少米?要解决这个问题,需要下面哪两个条件?( )和( )。
①小聪自行车的车轮外直径约60厘米;②小聪步行大约每分钟50米;③车轮平均每分钟转100圈;④小聪的自行车车身长1.5米。
A.①③ B.③④ C.①② D.②④
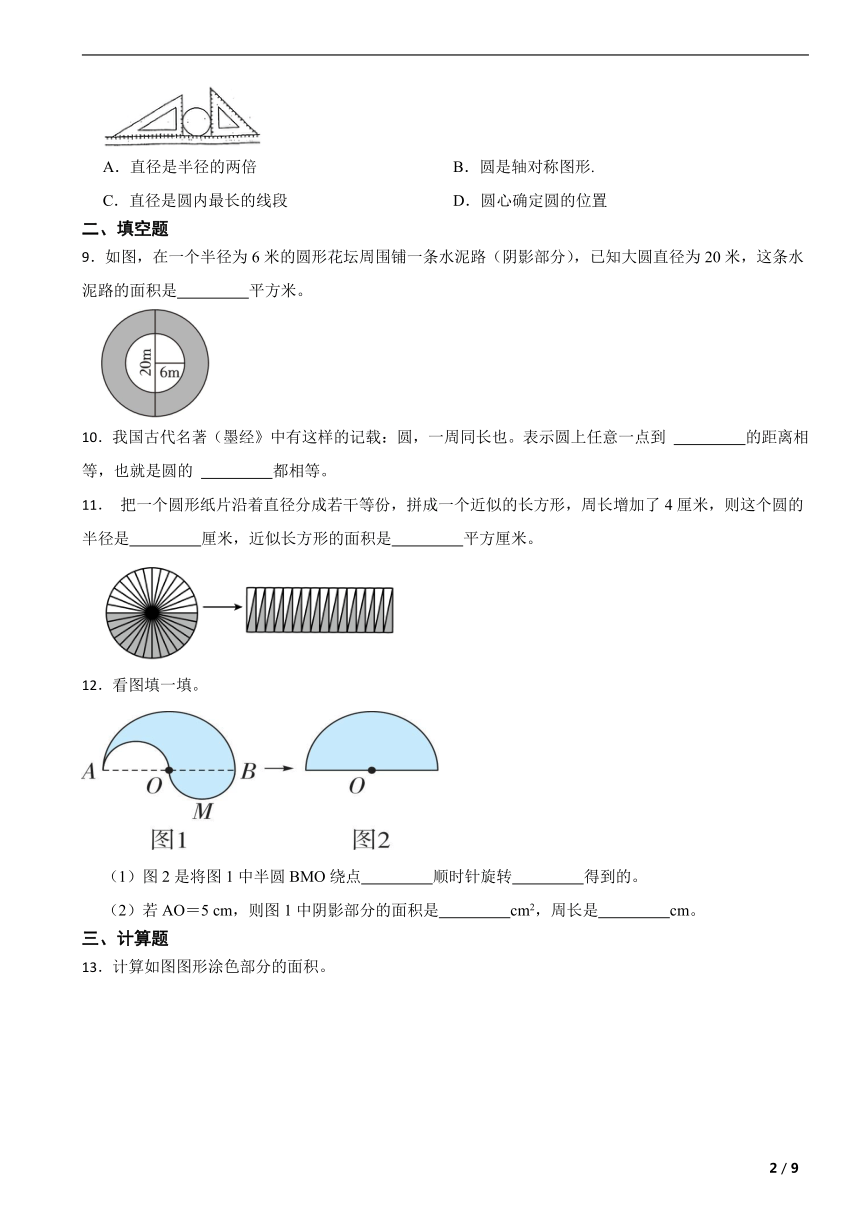
8.用下图方法测量圆的直径,依据是( )。
A.直径是半径的两倍 B.圆是轴对称图形.
C.直径是圆内最长的线段 D.圆心确定圆的位置
二、填空题
9.如图,在一个半径为6米的圆形花坛周围铺一条水泥路(阴影部分),已知大圆直径为20米,这条水泥路的面积是 平方米。
10.我国古代名著(墨经》中有这样的记载:圆,一周同长也。表示圆上任意一点到 的距离相等,也就是圆的 都相等。
11. 把一个圆形纸片沿着直径分成若干等份,拼成一个近似的长方形,周长增加了4厘米,则这个圆的半径是 厘米,近似长方形的面积是 平方厘米。
12.看图填一填。
(1)图2是将图1中半圆BMO绕点 顺时针旋转 得到的。
(2)若AO=5 cm,则图1中阴影部分的面积是 cm2,周长是 cm。
三、计算题
13.计算如图图形涂色部分的面积。
14.求阴影部分的面积。(cm)
四、解决问题
15.一个直径是10m的圆形喷水池,周围有一条环形小路,路宽3m,这条小路的面积是多少平方米?
16.阳光小区里有一个圆形花坛,周长为100.48 米,中间有一个底座为圆形的雕塑,底座半径为6米。这个花坛中除雕塑外的部分种满了太阳花,太阳花的种植面积是多少平方米?
17.一个圆形花坛的周长是62.8米,为了扩大种植的面积,将它的半径增加了2米后,它的面积是多少?
18.两个完全相同的半圆形玉佩,周长都是10.28厘米,如果把它们拼成一个完整的玉佩,玉佩的面积是多少平方厘米?
19.一个钟表的分针走一圈,针尖所走过的路程是50.24厘米。这个分针走一圈扫过的面积是多少平方厘米?
20.一个圆形喷水池的周长是94.2米,绕着这个水池修一条宽2米的水泥路,求路面的面积是多少?
答案解析部分
1.【答案】A
【解析】【解答】解:3.14×82
=3.14×64
=200.96(cm2)
故答案为:A。
【分析】 从下午3时到下午4时,分针转动了一圈,分针扫过的面积是一个圆的面积,圆的半径是分针的长度,S=πr2,据此列式解答。
2.【答案】A
【解析】【解答】解:车轮转动一周的路程就是车轮的周长。
故答案为:A。
【分析】圆的周长=2×π×半径,据此解答。
3.【答案】B
【解析】【解答】解:将圆剪拼成一个长方形,这个长方形的长等于圆周长的一半,也就是πr。
故答案为:B。
【分析】将圆剪拼成一个长方形,长方形的长就是圆周长的一半,宽就是圆的半径。
4.【答案】B
【解析】【解答】、、三个图形用阴影部分的面积都是正方形面积减去正方形内最大圆的面积;中阴影部分的面积与其他三个不同。
故答案为:B。
【分析】A:阴影部分的面积是正方形面积减去最大圆的面积;
B:空白部分是两个圆,这两个空白部分与正方形内最大圆的面积不相等;
C:空白部分四个圆刚好是正方形内最大的圆;
D:空白部分两个半圆合起来刚好是正方形内最大的圆。
5.【答案】D
【解析】【解答】解:3.14×3+3×2
=9.42+6
=15.42(厘米)
故答案为:D。
【分析】圆周长公式:C=2πr。半圆的周长包括圆周长的一半和一条直径的长度。由此用圆周长的一半加上直径的长度即可求出半圆的周长。
6.【答案】C
【解析】【解答】解:A:圆周率的近似数是3.14,原来说法错误;
B:圆的周长与圆的位置无关,原来说法错误;
C:直径是圆内最长的线段,此说法正确;
D:直径和半径都是线段,原来说法错误。
故答案为:C。
【分析】A:圆周率是一个无限不循环小数,3.14是其近似数;
B:圆的周长与圆的直径或半径的大小有关,与圆的位置无关;
C:直径是通过圆心并且两端都在圆上的线段,直径是圆内最长的线段;
D:半径是连接圆心到圆上任意一点的线段,直径和半径都是线段。
7.【答案】A
【解析】【解答】解:①知道车轮外直径,还需要知道车轮每分钟转多少圈,可以求出自行车每分钟行多少米,因此需要①③;②小聪是骑自行车,所以知道步行速度没有用;④知道车身长没有用;
故答案为:A。
【分析】已知时间要求路程还需要知道自行车的速度,也就是自行车每分钟行多少米,据此找到合适的条件。
8.【答案】C
【解析】【解答】解:这种测量方法的依据是直径是圆内最长的线段。
故答案为:C。
【分析】直径是圆内最大长的线段,可以用此方法进行测量。
9.【答案】200.96
【解析】【解答】解:20÷2=10(m)
3.14×(102-62)
=3.14×(100-36)
=3.14×64
=200.96(平方米)
故答案为:200.96。
【分析】观察图可知,水泥路是一个圆环,圆环的面积S=π(R2-r2),据此列式解答。
10.【答案】圆心;半径
【解析】【解答】解:圆上任意一点到圆心的距离相等,也就是圆的半径都相等。
故答案为:圆心;半径。
【分析】在同一圆里,所有的半径都相等,所有的直径都相等,直径等于半径的2倍。
11.【答案】2;12.56
【解析】【解答】解:半径:4÷2=2(厘米)
面积:3.14×22=12.56(平方厘米)
故答案为:2;12.56。
【分析】由图可知,长方形比圆形周长增加了2个圆的半径长度,因此,用增加周长长度÷2即可求出圆的半径;近似长方形的面积=圆面积=π×半径2。
12.【答案】(1)O;180°
(2)39.25;31.4
【解析】【解答】解:(1)图2是将图1中半圆BMO绕点O顺时针旋转180°得到的;
(2)3.14×52÷2
=78.5÷2
=39.25(平方厘米)
5×2×3.14
=10×3.14
=31.4(厘米)。
故答案为:(1)O;180°;(2)39.25;31.4。
【分析】(1)图2是将图1中半圆BMO绕点O顺时针旋转180°得到的;
(2)图1中阴影部分的面积=半圆的面积=π×半径2÷2;阴影部分的周长=圆的周长=π×半径×2。
13.【答案】解:(4+2)×2÷2﹣3.14×22÷4
=6﹣3.14
=2.86(平方厘米)
答:阴影部分的面积是2.86平方厘米
【解析】【分析】梯形的面积=(上底+下底)×高÷2,圆的面积=π×半径的平方÷4,梯形的面积-圆的面积=涂色部分的面积。
14.【答案】解:16÷2=8(cm)
3.14×82÷2-8×8÷2
=3.14×16-32
=50.24-32
=18.24(cm2)
【解析】【分析】阴影部分面积是半圆面积减去半圆内部空白部分等腰直角三角形的面积。等腰直角三角形的两条腰的长度是圆的半径。
15.【答案】解:10÷2=5(米)
5+3=8(米)
3.14×82﹣3.14×52
=3.14×(82﹣52)
=3.14×(64﹣25)
=3.14×39
=122.46(平方米)
答:这条小路的面积是122.46平方米。
【解析】【分析】这条小路的面积就是这个外圆半径为10÷2+3=8米,内圆半径为10÷2=5米的圆环的面积,由此利用圆环的面积公式即可计算。
16.【答案】解:100.48÷3.14÷2=16(米)
3.14×16×16-3.14×6×6
=803.84-113.04
=690.8(平方米)
答:太阳花的种植面积是690.8平方米。
【解析】【分析】圆的周长÷π÷2=圆的半径;π×半径的平方=圆的面积;外圆面积-内圆面积=太阳花的种植面积。
17.【答案】解: 62.8÷3.14÷2
=20÷2
=10(米)
10+2=12(米)
3.14×12×12
=37.68×12
=452.16(平方米)
答:它的面积是452.16平方米。
【解析】【分析】根据圆的周长÷3.14÷2=半径,求出原来的半径,再加上2米,求出现在的半径,再求面积即可。
18.【答案】解:设半圆的半径是r厘米,
2r+3.14r=10.28
5.14r=10.28
r=2
3.14×22=12.56(平方厘米)
答:玉佩的面积是12.56平方厘米。
【解析】【分析】根据题意知道10.28厘米是半圆形的周长,由半圆的周长公式即可求出半径,再根据圆的面积公式,即可求出答案。
19.【答案】解: 50.24÷3.14÷2
=16÷2
=8(厘米)
3.14×82
=3.14×64
=200.96(平方厘米)
答:这个分针走一圈扫过的面积是200.96平方厘米。
【解析】【分析】根据生活经验可知,分针1小时转一圈,分针走一圈,针尖走的路程等于以分针的长为半径的圆的周长,根据圆的周长公式:C=2πr,那么r=C÷2π,据此求出分针的长(半径),然后根据圆的面积公式:S=,把数据代入公式解答。
20.【答案】解: 94.2÷3.14÷2
=30÷2
=15(米)
15+2=17(米)
3.14×(-)
=3.14×64
=200.96(平方米)
答:路面的面积是200.96平方米。
【解析】【分析】根据题意,求路面面积即求圆环面积,可利用圆的周长公式确定圆形喷水池半径,即内圆的半径为(94.2÷3.14÷2)米,则圆环的外圆半径为(94.2÷3.14÷2+2)米,然后再根据圆环的面积公式代入数据进行计算即可得到路面的面积。
1 / 1
一、单选题
1.在一个钟面上,分针长8cm,时针长6cm,从下午3时到下午4时,分针扫过的面积是( )cm2。
A.200.96 B.113.04 C.50.24 D.28.26
2.车轮转动一周的路程就是车轮的( )
A.周长 B.直径 C.半径 D.面积
3.将圆剪拼成一个长方形,这个长方形的长等于( )
A.r B.πr C.2πr D.πr2
4.下列四个图案中,哪个图案的阴影部分面积与其他三个不同( )
A. B.
C. D.
5.一个半圆的半径是3厘米,它的周长是( )厘米。
A.18.84 B.9.42 C.12.42 D.15.42
6.下列说法中正确的是( )
A.圆周率就是3.14。
B.由于圆的位置不同,所以圆的周长不同。
C.直径是圆内最长的线段。
D.直径是线段,半径是射线。
7.小聪骑自行车到学校用10分钟,从小聪家到学校大约多少米?要解决这个问题,需要下面哪两个条件?( )和( )。
①小聪自行车的车轮外直径约60厘米;②小聪步行大约每分钟50米;③车轮平均每分钟转100圈;④小聪的自行车车身长1.5米。
A.①③ B.③④ C.①② D.②④
8.用下图方法测量圆的直径,依据是( )。
A.直径是半径的两倍 B.圆是轴对称图形.
C.直径是圆内最长的线段 D.圆心确定圆的位置
二、填空题
9.如图,在一个半径为6米的圆形花坛周围铺一条水泥路(阴影部分),已知大圆直径为20米,这条水泥路的面积是 平方米。
10.我国古代名著(墨经》中有这样的记载:圆,一周同长也。表示圆上任意一点到 的距离相等,也就是圆的 都相等。
11. 把一个圆形纸片沿着直径分成若干等份,拼成一个近似的长方形,周长增加了4厘米,则这个圆的半径是 厘米,近似长方形的面积是 平方厘米。
12.看图填一填。
(1)图2是将图1中半圆BMO绕点 顺时针旋转 得到的。
(2)若AO=5 cm,则图1中阴影部分的面积是 cm2,周长是 cm。
三、计算题
13.计算如图图形涂色部分的面积。
14.求阴影部分的面积。(cm)
四、解决问题
15.一个直径是10m的圆形喷水池,周围有一条环形小路,路宽3m,这条小路的面积是多少平方米?
16.阳光小区里有一个圆形花坛,周长为100.48 米,中间有一个底座为圆形的雕塑,底座半径为6米。这个花坛中除雕塑外的部分种满了太阳花,太阳花的种植面积是多少平方米?
17.一个圆形花坛的周长是62.8米,为了扩大种植的面积,将它的半径增加了2米后,它的面积是多少?
18.两个完全相同的半圆形玉佩,周长都是10.28厘米,如果把它们拼成一个完整的玉佩,玉佩的面积是多少平方厘米?
19.一个钟表的分针走一圈,针尖所走过的路程是50.24厘米。这个分针走一圈扫过的面积是多少平方厘米?
20.一个圆形喷水池的周长是94.2米,绕着这个水池修一条宽2米的水泥路,求路面的面积是多少?
答案解析部分
1.【答案】A
【解析】【解答】解:3.14×82
=3.14×64
=200.96(cm2)
故答案为:A。
【分析】 从下午3时到下午4时,分针转动了一圈,分针扫过的面积是一个圆的面积,圆的半径是分针的长度,S=πr2,据此列式解答。
2.【答案】A
【解析】【解答】解:车轮转动一周的路程就是车轮的周长。
故答案为:A。
【分析】圆的周长=2×π×半径,据此解答。
3.【答案】B
【解析】【解答】解:将圆剪拼成一个长方形,这个长方形的长等于圆周长的一半,也就是πr。
故答案为:B。
【分析】将圆剪拼成一个长方形,长方形的长就是圆周长的一半,宽就是圆的半径。
4.【答案】B
【解析】【解答】、、三个图形用阴影部分的面积都是正方形面积减去正方形内最大圆的面积;中阴影部分的面积与其他三个不同。
故答案为:B。
【分析】A:阴影部分的面积是正方形面积减去最大圆的面积;
B:空白部分是两个圆,这两个空白部分与正方形内最大圆的面积不相等;
C:空白部分四个圆刚好是正方形内最大的圆;
D:空白部分两个半圆合起来刚好是正方形内最大的圆。
5.【答案】D
【解析】【解答】解:3.14×3+3×2
=9.42+6
=15.42(厘米)
故答案为:D。
【分析】圆周长公式:C=2πr。半圆的周长包括圆周长的一半和一条直径的长度。由此用圆周长的一半加上直径的长度即可求出半圆的周长。
6.【答案】C
【解析】【解答】解:A:圆周率的近似数是3.14,原来说法错误;
B:圆的周长与圆的位置无关,原来说法错误;
C:直径是圆内最长的线段,此说法正确;
D:直径和半径都是线段,原来说法错误。
故答案为:C。
【分析】A:圆周率是一个无限不循环小数,3.14是其近似数;
B:圆的周长与圆的直径或半径的大小有关,与圆的位置无关;
C:直径是通过圆心并且两端都在圆上的线段,直径是圆内最长的线段;
D:半径是连接圆心到圆上任意一点的线段,直径和半径都是线段。
7.【答案】A
【解析】【解答】解:①知道车轮外直径,还需要知道车轮每分钟转多少圈,可以求出自行车每分钟行多少米,因此需要①③;②小聪是骑自行车,所以知道步行速度没有用;④知道车身长没有用;
故答案为:A。
【分析】已知时间要求路程还需要知道自行车的速度,也就是自行车每分钟行多少米,据此找到合适的条件。
8.【答案】C
【解析】【解答】解:这种测量方法的依据是直径是圆内最长的线段。
故答案为:C。
【分析】直径是圆内最大长的线段,可以用此方法进行测量。
9.【答案】200.96
【解析】【解答】解:20÷2=10(m)
3.14×(102-62)
=3.14×(100-36)
=3.14×64
=200.96(平方米)
故答案为:200.96。
【分析】观察图可知,水泥路是一个圆环,圆环的面积S=π(R2-r2),据此列式解答。
10.【答案】圆心;半径
【解析】【解答】解:圆上任意一点到圆心的距离相等,也就是圆的半径都相等。
故答案为:圆心;半径。
【分析】在同一圆里,所有的半径都相等,所有的直径都相等,直径等于半径的2倍。
11.【答案】2;12.56
【解析】【解答】解:半径:4÷2=2(厘米)
面积:3.14×22=12.56(平方厘米)
故答案为:2;12.56。
【分析】由图可知,长方形比圆形周长增加了2个圆的半径长度,因此,用增加周长长度÷2即可求出圆的半径;近似长方形的面积=圆面积=π×半径2。
12.【答案】(1)O;180°
(2)39.25;31.4
【解析】【解答】解:(1)图2是将图1中半圆BMO绕点O顺时针旋转180°得到的;
(2)3.14×52÷2
=78.5÷2
=39.25(平方厘米)
5×2×3.14
=10×3.14
=31.4(厘米)。
故答案为:(1)O;180°;(2)39.25;31.4。
【分析】(1)图2是将图1中半圆BMO绕点O顺时针旋转180°得到的;
(2)图1中阴影部分的面积=半圆的面积=π×半径2÷2;阴影部分的周长=圆的周长=π×半径×2。
13.【答案】解:(4+2)×2÷2﹣3.14×22÷4
=6﹣3.14
=2.86(平方厘米)
答:阴影部分的面积是2.86平方厘米
【解析】【分析】梯形的面积=(上底+下底)×高÷2,圆的面积=π×半径的平方÷4,梯形的面积-圆的面积=涂色部分的面积。
14.【答案】解:16÷2=8(cm)
3.14×82÷2-8×8÷2
=3.14×16-32
=50.24-32
=18.24(cm2)
【解析】【分析】阴影部分面积是半圆面积减去半圆内部空白部分等腰直角三角形的面积。等腰直角三角形的两条腰的长度是圆的半径。
15.【答案】解:10÷2=5(米)
5+3=8(米)
3.14×82﹣3.14×52
=3.14×(82﹣52)
=3.14×(64﹣25)
=3.14×39
=122.46(平方米)
答:这条小路的面积是122.46平方米。
【解析】【分析】这条小路的面积就是这个外圆半径为10÷2+3=8米,内圆半径为10÷2=5米的圆环的面积,由此利用圆环的面积公式即可计算。
16.【答案】解:100.48÷3.14÷2=16(米)
3.14×16×16-3.14×6×6
=803.84-113.04
=690.8(平方米)
答:太阳花的种植面积是690.8平方米。
【解析】【分析】圆的周长÷π÷2=圆的半径;π×半径的平方=圆的面积;外圆面积-内圆面积=太阳花的种植面积。
17.【答案】解: 62.8÷3.14÷2
=20÷2
=10(米)
10+2=12(米)
3.14×12×12
=37.68×12
=452.16(平方米)
答:它的面积是452.16平方米。
【解析】【分析】根据圆的周长÷3.14÷2=半径,求出原来的半径,再加上2米,求出现在的半径,再求面积即可。
18.【答案】解:设半圆的半径是r厘米,
2r+3.14r=10.28
5.14r=10.28
r=2
3.14×22=12.56(平方厘米)
答:玉佩的面积是12.56平方厘米。
【解析】【分析】根据题意知道10.28厘米是半圆形的周长,由半圆的周长公式即可求出半径,再根据圆的面积公式,即可求出答案。
19.【答案】解: 50.24÷3.14÷2
=16÷2
=8(厘米)
3.14×82
=3.14×64
=200.96(平方厘米)
答:这个分针走一圈扫过的面积是200.96平方厘米。
【解析】【分析】根据生活经验可知,分针1小时转一圈,分针走一圈,针尖走的路程等于以分针的长为半径的圆的周长,根据圆的周长公式:C=2πr,那么r=C÷2π,据此求出分针的长(半径),然后根据圆的面积公式:S=,把数据代入公式解答。
20.【答案】解: 94.2÷3.14÷2
=30÷2
=15(米)
15+2=17(米)
3.14×(-)
=3.14×64
=200.96(平方米)
答:路面的面积是200.96平方米。
【解析】【分析】根据题意,求路面面积即求圆环面积,可利用圆的周长公式确定圆形喷水池半径,即内圆的半径为(94.2÷3.14÷2)米,则圆环的外圆半径为(94.2÷3.14÷2+2)米,然后再根据圆环的面积公式代入数据进行计算即可得到路面的面积。
1 / 1
