22.1.4 课时1 二次函数y=ax2+bx+c的图象和性质 分层练习(含答案) 2023-2024学年数学人教版九年级上册
文档属性
| 名称 | 22.1.4 课时1 二次函数y=ax2+bx+c的图象和性质 分层练习(含答案) 2023-2024学年数学人教版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 186.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 00:00:00 | ||
图片预览

文档简介
22.1.4 课时1 二次函数y=ax2+bx+c的图象和性质
【练基础】
必备知识1 二次函数y=ax2+bx+c与y=a(x-h)2+k的关系
1.把二次函数y=x2-4x-3化成y=a(x-h)2+k的形式,正确的是 ( )
A.y=(x-2)2-1 B.y=(x-2)2+1
C.y=(x-2)2-7 D.y=(x+2)+1
2.若二次函数y=x2-mx+6配方后为y=(x-2)2+k,则m,k的值分别为 ( )
A.0,6 B.0,2 C.4,6 D.4,2
3.将抛物线y=x2-6x+21向左平移2个单位长度,再向上平移2个单位长度,得到的抛物线的解析式为 ( )
A.y=(x-8)2+5 B.y=(x-4)2+5
C.y=(x-8)2+3 D.y=(x-4)2+3
必备知识2 二次函数y=ax2+bx+c的图象和性质
4.抛物线y=-x2+4x+2的对称轴是 ( )
A.直线x=2 B.直线x=-2
C.直线x=1 D.直线x=-1
5.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表,则该抛物线的对称轴是直线 ( )
x -1 1 5
y 2 5 2
A.x=3 B.x=2
C.x=1.5 D.x=1
6.已知(-3,y1),(-2,y2),(1,y3)是抛物线y=-3x2-12x+m上的点,则 ( )
A.y3C.y27.二次函数y=2x2+bx+3的图象的对称轴是直线x=1,则常数b的值为 .
8.【改编】若抛物线y=x2-(b+2)x+9的顶点在y轴上,则b= ;若抛物线y=x2-8x+m+6的顶点在x轴上,则m= .
必备知识3 二次函数y=ax2+bx+c(a≠0)的图象与a,b,c的关系
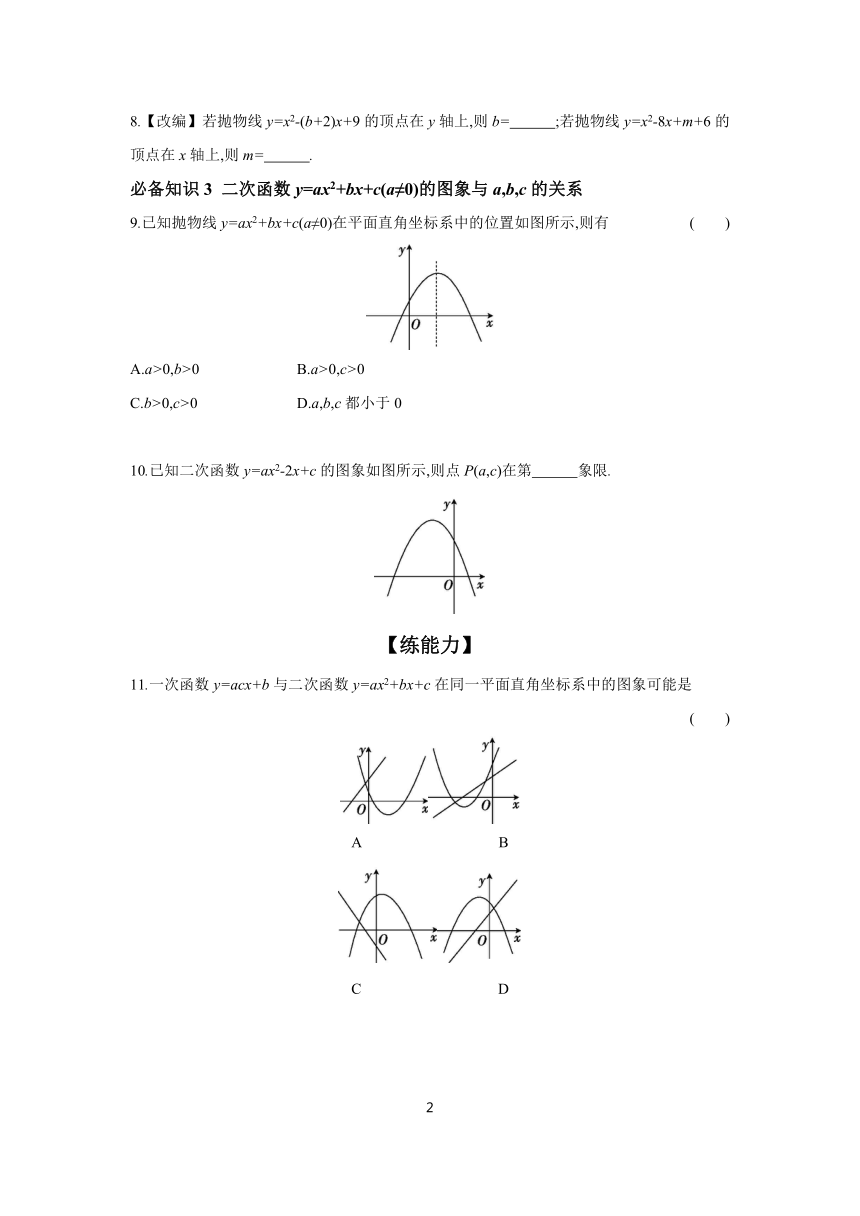
9.已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则有 ( )
A.a>0,b>0 B.a>0,c>0
C.b>0,c>0 D.a,b,c都小于0
10.已知二次函数y=ax2-2x+c的图象如图所示,则点P(a,c)在第 象限.
【练能力】
11.一次函数y=acx+b与二次函数y=ax2+bx+c在同一平面直角坐标系中的图象可能是 ( )
A B
C D
12.老师设计了接力游戏,用合作的方式完成“求抛物线y=2x2+4x-4的顶点坐标”,规则如下:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成解答.过程如图所示:
接力中,自己负责的一步出现错误的是 ( )
A.只有丁 B.乙和丁
C.乙和丙 D.甲和丁
13.已知函数y=ax2-2ax-1(a是常数,a≠0),下列结论正确的是 ( )
A.当a=1时,函数图象经过点(-1,1)
B.当a=-2时,函数图象与x轴没有交点
C.若a>0,则当x≥1时,y随x的增大而减小
D.若a<0,则当x≤1时,y随x的增大而增大
14.在平面直角坐标系xOy中,四条抛物线如图所示,其解析式中的二次项系数一定小于1的是 ( )
A.y1 B.y2 C.y3 D.y4
15.如图,抛物线y=ax2+bx+c与x轴相交于点A、B(m+2,0),与y轴相交于点C,点D在该抛物线上,坐标为(m,c),则点A的坐标是 .
16.【石家庄月考】如图,已知二次函数y=x2+ax+3的图象经过点P(-2,3).
(1)求a的值和图象的顶点坐标.
(2)点Q(m,n)在该二次函数图象上.
①当m=2时,求n的值;
②若点Q到y轴的距离小于2,请根据图象直接写出n的取值范围.
【练素养】
17.阅读材料:设二次函数y1,y2的图象的顶点坐标分别为(h,k),(m,n),若h=2m,k=2n,且开口方向相同,则称y1是y2的“同倍二次函数”.
(1)请写出二次函数y=x2-2x+2的一个“同倍二次函数”: .
(2)已知关于x的二次函数y1=x-2-和二次函数y2=2x2-ax+1,若函数y1恰是y2的“同倍二次函数”,求a的值.
参考答案
练基础
1.C 2.D 3.B 4.A 5.B 6.B 7.-4 8.-2 10 9.C 10.二
练能力
11.B 12.D 13.D 14.A 15.(-2,0)
16.【解析】(1)把P(-2,3)代入y=x2+ax+3,
得4-2a+3=3,∴a=2,∴y=x2+2x+3=(x+1)2+2,
∴图象的顶点坐标为(-1,2).
(2)①由题意知点Q(2,n)在该二次函数图象上,
∴n=4+4+3=11.
②n的取值范围是2≤n<11.
提示:∵点Q到y轴的距离小于2,
∴|m|<2,∴-2练素养
17.【解析】(1)y=(x-2)2+2.(答案不唯一)
提示:∵y=x2-2x+2=(x-1)2+1,
∴该图象顶点坐标为(1,1),
∴y=x2-2x+2的“同倍二次函数”可以是y=(x-2)2+2.
(2)∵二次函数y1=x-2-的顶点坐标为,-,
∴函数y2=2x2-ax+1图象的顶点坐标为,-,
把,-代入y2=2x2-ax+1得-=22-a·+1,
解得a=-2或a=4.
2
【练基础】
必备知识1 二次函数y=ax2+bx+c与y=a(x-h)2+k的关系
1.把二次函数y=x2-4x-3化成y=a(x-h)2+k的形式,正确的是 ( )
A.y=(x-2)2-1 B.y=(x-2)2+1
C.y=(x-2)2-7 D.y=(x+2)+1
2.若二次函数y=x2-mx+6配方后为y=(x-2)2+k,则m,k的值分别为 ( )
A.0,6 B.0,2 C.4,6 D.4,2
3.将抛物线y=x2-6x+21向左平移2个单位长度,再向上平移2个单位长度,得到的抛物线的解析式为 ( )
A.y=(x-8)2+5 B.y=(x-4)2+5
C.y=(x-8)2+3 D.y=(x-4)2+3
必备知识2 二次函数y=ax2+bx+c的图象和性质
4.抛物线y=-x2+4x+2的对称轴是 ( )
A.直线x=2 B.直线x=-2
C.直线x=1 D.直线x=-1
5.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表,则该抛物线的对称轴是直线 ( )
x -1 1 5
y 2 5 2
A.x=3 B.x=2
C.x=1.5 D.x=1
6.已知(-3,y1),(-2,y2),(1,y3)是抛物线y=-3x2-12x+m上的点,则 ( )
A.y3
8.【改编】若抛物线y=x2-(b+2)x+9的顶点在y轴上,则b= ;若抛物线y=x2-8x+m+6的顶点在x轴上,则m= .
必备知识3 二次函数y=ax2+bx+c(a≠0)的图象与a,b,c的关系
9.已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则有 ( )
A.a>0,b>0 B.a>0,c>0
C.b>0,c>0 D.a,b,c都小于0
10.已知二次函数y=ax2-2x+c的图象如图所示,则点P(a,c)在第 象限.
【练能力】
11.一次函数y=acx+b与二次函数y=ax2+bx+c在同一平面直角坐标系中的图象可能是 ( )
A B
C D
12.老师设计了接力游戏,用合作的方式完成“求抛物线y=2x2+4x-4的顶点坐标”,规则如下:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成解答.过程如图所示:
接力中,自己负责的一步出现错误的是 ( )
A.只有丁 B.乙和丁
C.乙和丙 D.甲和丁
13.已知函数y=ax2-2ax-1(a是常数,a≠0),下列结论正确的是 ( )
A.当a=1时,函数图象经过点(-1,1)
B.当a=-2时,函数图象与x轴没有交点
C.若a>0,则当x≥1时,y随x的增大而减小
D.若a<0,则当x≤1时,y随x的增大而增大
14.在平面直角坐标系xOy中,四条抛物线如图所示,其解析式中的二次项系数一定小于1的是 ( )
A.y1 B.y2 C.y3 D.y4
15.如图,抛物线y=ax2+bx+c与x轴相交于点A、B(m+2,0),与y轴相交于点C,点D在该抛物线上,坐标为(m,c),则点A的坐标是 .
16.【石家庄月考】如图,已知二次函数y=x2+ax+3的图象经过点P(-2,3).
(1)求a的值和图象的顶点坐标.
(2)点Q(m,n)在该二次函数图象上.
①当m=2时,求n的值;
②若点Q到y轴的距离小于2,请根据图象直接写出n的取值范围.
【练素养】
17.阅读材料:设二次函数y1,y2的图象的顶点坐标分别为(h,k),(m,n),若h=2m,k=2n,且开口方向相同,则称y1是y2的“同倍二次函数”.
(1)请写出二次函数y=x2-2x+2的一个“同倍二次函数”: .
(2)已知关于x的二次函数y1=x-2-和二次函数y2=2x2-ax+1,若函数y1恰是y2的“同倍二次函数”,求a的值.
参考答案
练基础
1.C 2.D 3.B 4.A 5.B 6.B 7.-4 8.-2 10 9.C 10.二
练能力
11.B 12.D 13.D 14.A 15.(-2,0)
16.【解析】(1)把P(-2,3)代入y=x2+ax+3,
得4-2a+3=3,∴a=2,∴y=x2+2x+3=(x+1)2+2,
∴图象的顶点坐标为(-1,2).
(2)①由题意知点Q(2,n)在该二次函数图象上,
∴n=4+4+3=11.
②n的取值范围是2≤n<11.
提示:∵点Q到y轴的距离小于2,
∴|m|<2,∴-2
17.【解析】(1)y=(x-2)2+2.(答案不唯一)
提示:∵y=x2-2x+2=(x-1)2+1,
∴该图象顶点坐标为(1,1),
∴y=x2-2x+2的“同倍二次函数”可以是y=(x-2)2+2.
(2)∵二次函数y1=x-2-的顶点坐标为,-,
∴函数y2=2x2-ax+1图象的顶点坐标为,-,
把,-代入y2=2x2-ax+1得-=22-a·+1,
解得a=-2或a=4.
2
同课章节目录
