22.1.4 课时2 用待定系数法求二次函数的解析式 分层练习(含答案) 2023-2024学年数学人教版九年级上册
文档属性
| 名称 | 22.1.4 课时2 用待定系数法求二次函数的解析式 分层练习(含答案) 2023-2024学年数学人教版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 85.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-16 17:08:15 | ||
图片预览

文档简介
22.1.4 课时2 用待定系数法求二次函数的解析式
【练基础】
必备知识1 三点式确定二次函数的解析式
1.已知二次函数y=ax2+bx+c的图象如图所示,则其函数解析式是 ( )
A.y=x2-4x+5
B.y=-x2-4x+5
C.y=x2+4x+5
D.y=-x2+4x+5
2.已知某二次函数的图象过(0,1),(1,0),(-2,0)三点,则这个二次函数的解析式是 .
必备知识2 顶点式确定二次函数的解析式
3.某抛物线的形状、开口方向与抛物线y=3x2完全相同,顶点坐标是(-2,4),则该抛物线的解析式为 ( )
A.y=-3(x+2)2+4 B.y=3(x+2)2+4
C.y=-3(x-2)2+4 D.y=3(x-2)2+4
必备知识3 交点式确定二次函数的解析式
4.已知抛物线经过点A(2,0)和点B(-1,0),且与y轴交于x轴上方点C,若OC=2,则这条抛物线的解析式是 ( )
A.y=x2-x-2 B.y=-x2-x-2
C.y=-x2-x+2 D.y=-x2+x+2
5.已知抛物线与x轴交点的横坐标分别为3,1,与y轴交点的纵坐标为6,则该二次函数的解析式为 .
【练能力】
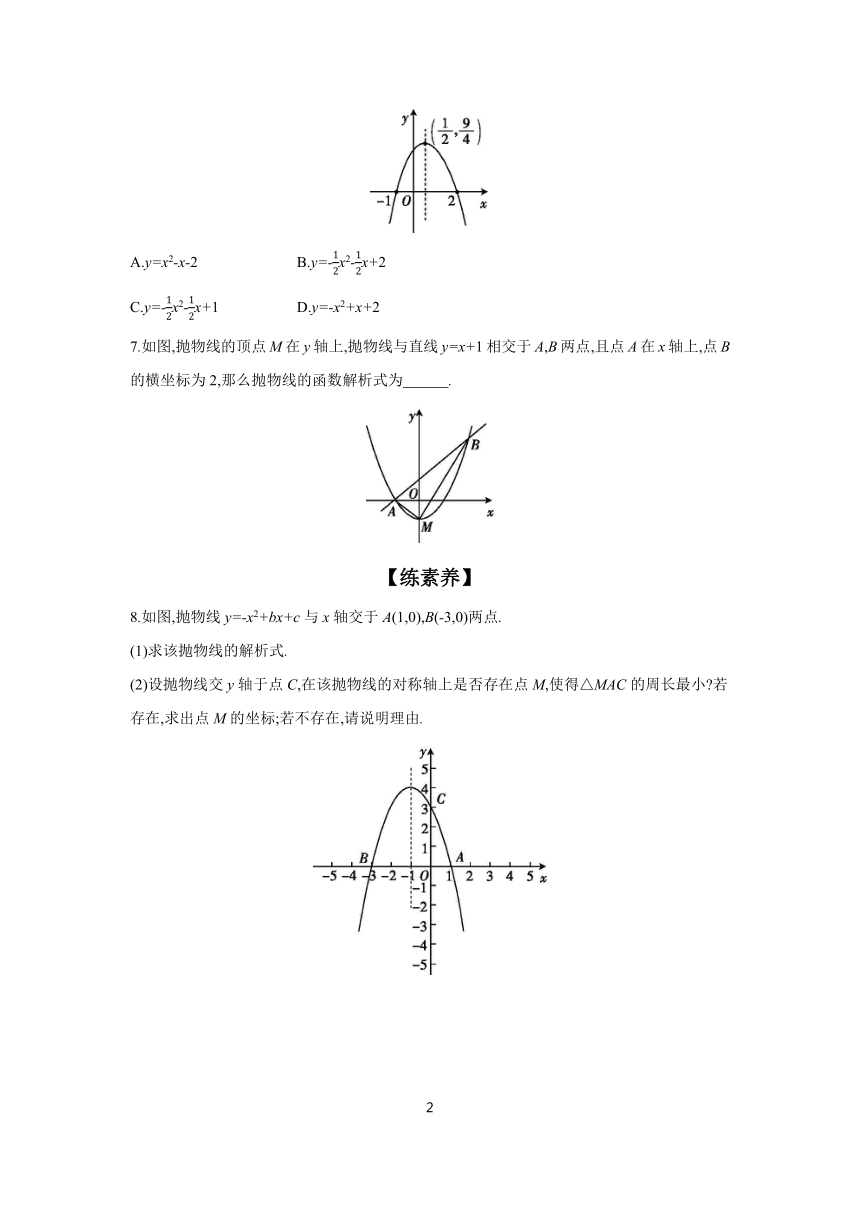
6.如图,这是某个二次函数的图象,根据图象可知,该二次函数的解析式是 ( )
A.y=x2-x-2 B.y=-x2-x+2
C.y=-x2-x+1 D.y=-x2+x+2
7.如图,抛物线的顶点M在y轴上,抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,点B的横坐标为2,那么抛物线的函数解析式为 .
【练素养】
8.如图,抛物线y=-x2+bx+c与x轴交于A(1,0),B(-3,0)两点.
(1)求该抛物线的解析式.
(2)设抛物线交y轴于点C,在该抛物线的对称轴上是否存在点M,使得△MAC的周长最小 若存在,求出点M的坐标;若不存在,请说明理由.
参考答案
练基础
1.B 2.y=-x2-x+1 3.B 4.D
5.y=2x2-8x+6
练能力
6.D 7.y=x2-1
练素养
8.【解析】(1)把点A(1,0),B(-3,0)代入y=-x2+bx+c,
得解得
∴该抛物线的解析式为y=-x2-2x+3.
(2)存在.连接BC交对称轴于点M(图略),则此时△MAC的周长最小.在y=-x2-2x+3中,令x=0,得y=3,∴点C的坐标为(0,3).
设直线BC的解析式为y=kx+n,
∴解得
∴直线BC的解析式为y=x+3.
∵抛物线y=-x2-2x+3的对称轴为直线x=-1,
∴当x=-1时,y=2,∴点M的坐标为(-1,2).
2
【练基础】
必备知识1 三点式确定二次函数的解析式
1.已知二次函数y=ax2+bx+c的图象如图所示,则其函数解析式是 ( )
A.y=x2-4x+5
B.y=-x2-4x+5
C.y=x2+4x+5
D.y=-x2+4x+5
2.已知某二次函数的图象过(0,1),(1,0),(-2,0)三点,则这个二次函数的解析式是 .
必备知识2 顶点式确定二次函数的解析式
3.某抛物线的形状、开口方向与抛物线y=3x2完全相同,顶点坐标是(-2,4),则该抛物线的解析式为 ( )
A.y=-3(x+2)2+4 B.y=3(x+2)2+4
C.y=-3(x-2)2+4 D.y=3(x-2)2+4
必备知识3 交点式确定二次函数的解析式
4.已知抛物线经过点A(2,0)和点B(-1,0),且与y轴交于x轴上方点C,若OC=2,则这条抛物线的解析式是 ( )
A.y=x2-x-2 B.y=-x2-x-2
C.y=-x2-x+2 D.y=-x2+x+2
5.已知抛物线与x轴交点的横坐标分别为3,1,与y轴交点的纵坐标为6,则该二次函数的解析式为 .
【练能力】
6.如图,这是某个二次函数的图象,根据图象可知,该二次函数的解析式是 ( )
A.y=x2-x-2 B.y=-x2-x+2
C.y=-x2-x+1 D.y=-x2+x+2
7.如图,抛物线的顶点M在y轴上,抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,点B的横坐标为2,那么抛物线的函数解析式为 .
【练素养】
8.如图,抛物线y=-x2+bx+c与x轴交于A(1,0),B(-3,0)两点.
(1)求该抛物线的解析式.
(2)设抛物线交y轴于点C,在该抛物线的对称轴上是否存在点M,使得△MAC的周长最小 若存在,求出点M的坐标;若不存在,请说明理由.
参考答案
练基础
1.B 2.y=-x2-x+1 3.B 4.D
5.y=2x2-8x+6
练能力
6.D 7.y=x2-1
练素养
8.【解析】(1)把点A(1,0),B(-3,0)代入y=-x2+bx+c,
得解得
∴该抛物线的解析式为y=-x2-2x+3.
(2)存在.连接BC交对称轴于点M(图略),则此时△MAC的周长最小.在y=-x2-2x+3中,令x=0,得y=3,∴点C的坐标为(0,3).
设直线BC的解析式为y=kx+n,
∴解得
∴直线BC的解析式为y=x+3.
∵抛物线y=-x2-2x+3的对称轴为直线x=-1,
∴当x=-1时,y=2,∴点M的坐标为(-1,2).
2
同课章节目录
