2023-2024学年数学人教版九年级上册23.1 图形的旋转 分层练习(含答案)
文档属性
| 名称 | 2023-2024学年数学人教版九年级上册23.1 图形的旋转 分层练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 401.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 15:23:58 | ||
图片预览


文档简介
23.1 图形的旋转
【练基础】
必备知识1 旋转的相关概念
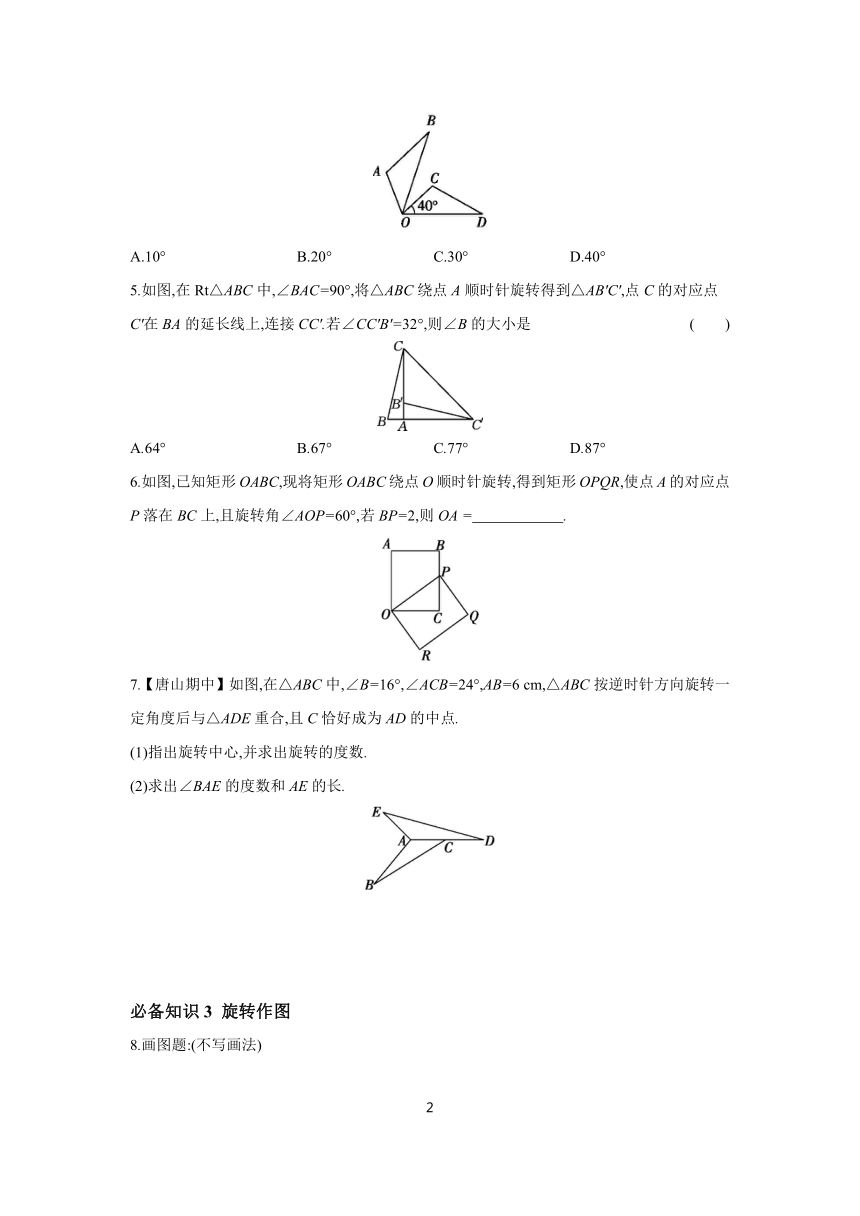
1.数学来源于生活,下列生活中的运动属于旋转的是 ( )
A.国旗上升的过程
B.球场上滚动的足球
C.工作中的风力发电机叶片
D.传输带运输的东西
2.如图,将网格纸中的图形绕点O逆时针旋转90°后得到的图形是 ( )
A B C D
3.如图,△ACB和△DCE都是直角三角形,其中一个三角形是由另一个三角形旋转得到的,则下列叙述中错误的是 ( )
A.旋转中心是点C
B.旋转角是90°
C.既可以看成逆时针旋转又可以看成顺时针旋转
D.旋转中心是点B,旋转角是∠ABC
必备知识2 旋转的性质
4.如图,将△AOB绕着点O顺时针旋转70°,得到△COD,若∠COD=40°,则∠BOC的度数为 ( )
A.10° B.20° C.30° D.40°
5.如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转得到△AB'C',点C的对应点C'在BA的延长线上,连接CC'.若∠CC'B'=32°,则∠B的大小是 ( )
A.64° B.67° C.77° D.87°
6.如图,已知矩形OABC,现将矩形OABC绕点O顺时针旋转,得到矩形OPQR,使点A的对应点P落在BC上,且旋转角∠AOP=60°,若BP=2,则OA = .
7.【唐山期中】如图,在△ABC中,∠B=16°,∠ACB=24°,AB=6 cm,△ABC按逆时针方向旋转一定角度后与△ADE重合,且C恰好成为AD的中点.
(1)指出旋转中心,并求出旋转的度数.
(2)求出∠BAE的度数和AE的长.
必备知识3 旋转作图
8.画图题:(不写画法)
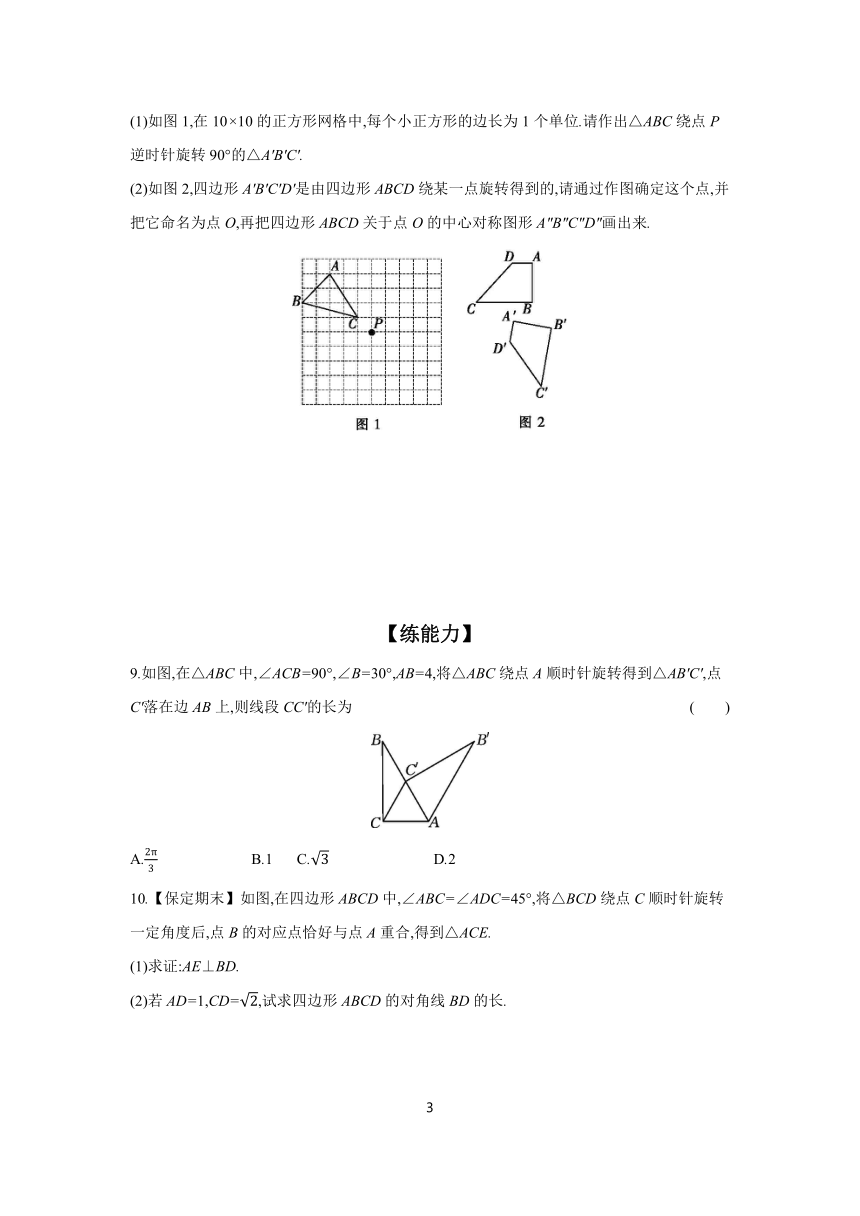
(1)如图1,在10×10的正方形网格中,每个小正方形的边长为1个单位.请作出△ABC绕点P逆时针旋转90°的△A'B'C'.
(2)如图2,四边形A'B'C'D'是由四边形ABCD绕某一点旋转得到的,请通过作图确定这个点,并把它命名为点O,再把四边形ABCD关于点O的中心对称图形A″B″C″D″画出来.
【练能力】
9.如图,在△ABC中,∠ACB=90°,∠B=30°,AB=4,将△ABC绕点A顺时针旋转得到△AB'C',点C'落在边AB上,则线段CC'的长为 ( )
A. B.1 C. D.2
10.【保定期末】如图,在四边形ABCD中,∠ABC=∠ADC=45°,将△BCD绕点C顺时针旋转一定角度后,点B的对应点恰好与点A重合,得到△ACE.
(1)求证:AE⊥BD.
(2)若AD=1,CD=,试求四边形ABCD的对角线BD的长.
11.如图,将一块含30°角的直角三角板OAB绕直角顶点O顺时针旋转x°(0(1)当x=30时,判断△AOE的形状,并说明理由.
(2)请你探索是否存在x,使△BDE是等腰三角形 若存在,请求出x的值;若不存在,请说明理由.
【练素养】
12.(1)如图1,O是等边△ABC内一点,连接OA,OB,OC,且OA=3,OB=4,OC=5,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.
填空:①旋转角的度数为 .
②线段OD的长为 .
③∠BDC的度数为 .
(2)如图2,O是等腰直角△ABC(∠ABC=90°)内一点,连接OA,OB,OC,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.当OA,OB,OC满足什么条件时,∠ODC=90° 请给出证明.
参考答案
练基础
1.C 2.C 3.D 4.C
5.C 【解析】解法一
解法二
6.4
7.【解析】(1)∵△ABC逆时针旋转一定角度后与△ADE重合,A为顶点,
∴旋转中心是点A.
根据旋转的性质可知:∠CAE=∠BAD=180°-∠B-∠ACB=140°,
∴旋转角度是140°.
(2)由旋转可知:△ABC≌△ADE,
∴AB=AD,AC=AE,∠BAC=∠EAD=140°,
∴∠BAE=360°-140°×2=80°.
∵C为AD的中点,
∴AC=AE=AB=×6=3(cm).
8.【解析】(1)如图1,△A'B'C'即所求.
(2)如图2,四边形A″B″C″D″即所求.
练能力
9.D
10.【解析】(1)证明:由题意可得AC=BC,∠ABC=45°,
∴∠BCA=90°.
设BD与AC,AE分别交于点M,N,
∵∠AMN=∠BMC,∠CAE=∠CBD,
∴∠ANM=∠MCB=90°.
即AE⊥BD.
(2)如图,连接DE.
∵∠BCD=∠ACE,
∴∠DCE=∠ACB=90°.
∵CD=CE=,
∴DE=2,∠CDE=45°,
∴∠ADE=∠ADC+∠CDE=90°,
∴AE=,
∴BD=.
11.【解析】(1)△AOE是等边三角形.
理由:∵∠AOB=90°,x°=30°,∴∠AOE=60°.
∵∠A=60°,∴∠A=∠AOE=60°,
∴△AOE是等边三角形.
(2)∵直角三角板OAB绕点O旋转得到△OCD,∴OB=OD,
∴∠BDE=∠OBD=(180°-x°),
∴∠DBE=∠OBD-∠ABO=(180°-x°)-30°,
∠BED=∠ABO+∠BOD=30°+x°.
△BDE是等腰三角形,分三种情况讨论:
①当∠BDE=∠DBE时,(180°-x°)=(180°-x°)-30°,无解;
②当∠BDE=∠BED时,(180°-x°)=30°+x°,解得x=40;
③当∠DBE=∠BED时,
(180°-x°)-30°=30°+x°,解得x=20.
综上所述,当x为20或40时,△BDE是等腰三角形.
练素养
12.【解析】(1)①∵△ABC为等边三角形,
∴BA=BC,∠ABC=60°.
∵△BAO绕点B顺时针旋转后得到△BCD,
∴∠OBD=∠ABC=60°,
∴旋转角的度数为60°.
②∵△BAO绕点B顺时针旋转后得到△BCD,
∴BO=BD,而∠OBD=60°,
∴△OBD为等边三角形,∴OD=OB=4.
③∵△BOD为等边三角形,∴∠BDO=60°.
∵△BAO绕点B顺时针旋转后得到△BCD,
∴CD=AO=3.
在△OCD中,CD=3,OD=4,OC=5,
∵32+42=52,∴CD2+OD2=OC2,
∴△OCD为直角三角形,∠ODC=90°,
∴∠BDC=∠BDO+∠ODC=60°+90°=150°.
(2)当OA2+2OB2=OC2时,∠ODC=90°.
理由如下:
∵△BAO绕点B顺时针旋转后得到△BCD,
∴∠OBD=∠ABC=90°,BO=BD,CD=AO,
∴△OBD为等腰直角三角形,
∴OD=OB.
∵当CD2+OD2=OC2时,△OCD为直角三角形,∠ODC=90°,
∴OA2+2OB2=OC2,
∴当OA,OB,OC满足OA2+2OB2=OC2时,∠ODC=90°.
2
【练基础】
必备知识1 旋转的相关概念
1.数学来源于生活,下列生活中的运动属于旋转的是 ( )
A.国旗上升的过程
B.球场上滚动的足球
C.工作中的风力发电机叶片
D.传输带运输的东西
2.如图,将网格纸中的图形绕点O逆时针旋转90°后得到的图形是 ( )
A B C D
3.如图,△ACB和△DCE都是直角三角形,其中一个三角形是由另一个三角形旋转得到的,则下列叙述中错误的是 ( )
A.旋转中心是点C
B.旋转角是90°
C.既可以看成逆时针旋转又可以看成顺时针旋转
D.旋转中心是点B,旋转角是∠ABC
必备知识2 旋转的性质
4.如图,将△AOB绕着点O顺时针旋转70°,得到△COD,若∠COD=40°,则∠BOC的度数为 ( )
A.10° B.20° C.30° D.40°
5.如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转得到△AB'C',点C的对应点C'在BA的延长线上,连接CC'.若∠CC'B'=32°,则∠B的大小是 ( )
A.64° B.67° C.77° D.87°
6.如图,已知矩形OABC,现将矩形OABC绕点O顺时针旋转,得到矩形OPQR,使点A的对应点P落在BC上,且旋转角∠AOP=60°,若BP=2,则OA = .
7.【唐山期中】如图,在△ABC中,∠B=16°,∠ACB=24°,AB=6 cm,△ABC按逆时针方向旋转一定角度后与△ADE重合,且C恰好成为AD的中点.
(1)指出旋转中心,并求出旋转的度数.
(2)求出∠BAE的度数和AE的长.
必备知识3 旋转作图
8.画图题:(不写画法)
(1)如图1,在10×10的正方形网格中,每个小正方形的边长为1个单位.请作出△ABC绕点P逆时针旋转90°的△A'B'C'.
(2)如图2,四边形A'B'C'D'是由四边形ABCD绕某一点旋转得到的,请通过作图确定这个点,并把它命名为点O,再把四边形ABCD关于点O的中心对称图形A″B″C″D″画出来.
【练能力】
9.如图,在△ABC中,∠ACB=90°,∠B=30°,AB=4,将△ABC绕点A顺时针旋转得到△AB'C',点C'落在边AB上,则线段CC'的长为 ( )
A. B.1 C. D.2
10.【保定期末】如图,在四边形ABCD中,∠ABC=∠ADC=45°,将△BCD绕点C顺时针旋转一定角度后,点B的对应点恰好与点A重合,得到△ACE.
(1)求证:AE⊥BD.
(2)若AD=1,CD=,试求四边形ABCD的对角线BD的长.
11.如图,将一块含30°角的直角三角板OAB绕直角顶点O顺时针旋转x°(0
(2)请你探索是否存在x,使△BDE是等腰三角形 若存在,请求出x的值;若不存在,请说明理由.
【练素养】
12.(1)如图1,O是等边△ABC内一点,连接OA,OB,OC,且OA=3,OB=4,OC=5,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.
填空:①旋转角的度数为 .
②线段OD的长为 .
③∠BDC的度数为 .
(2)如图2,O是等腰直角△ABC(∠ABC=90°)内一点,连接OA,OB,OC,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.当OA,OB,OC满足什么条件时,∠ODC=90° 请给出证明.
参考答案
练基础
1.C 2.C 3.D 4.C
5.C 【解析】解法一
解法二
6.4
7.【解析】(1)∵△ABC逆时针旋转一定角度后与△ADE重合,A为顶点,
∴旋转中心是点A.
根据旋转的性质可知:∠CAE=∠BAD=180°-∠B-∠ACB=140°,
∴旋转角度是140°.
(2)由旋转可知:△ABC≌△ADE,
∴AB=AD,AC=AE,∠BAC=∠EAD=140°,
∴∠BAE=360°-140°×2=80°.
∵C为AD的中点,
∴AC=AE=AB=×6=3(cm).
8.【解析】(1)如图1,△A'B'C'即所求.
(2)如图2,四边形A″B″C″D″即所求.
练能力
9.D
10.【解析】(1)证明:由题意可得AC=BC,∠ABC=45°,
∴∠BCA=90°.
设BD与AC,AE分别交于点M,N,
∵∠AMN=∠BMC,∠CAE=∠CBD,
∴∠ANM=∠MCB=90°.
即AE⊥BD.
(2)如图,连接DE.
∵∠BCD=∠ACE,
∴∠DCE=∠ACB=90°.
∵CD=CE=,
∴DE=2,∠CDE=45°,
∴∠ADE=∠ADC+∠CDE=90°,
∴AE=,
∴BD=.
11.【解析】(1)△AOE是等边三角形.
理由:∵∠AOB=90°,x°=30°,∴∠AOE=60°.
∵∠A=60°,∴∠A=∠AOE=60°,
∴△AOE是等边三角形.
(2)∵直角三角板OAB绕点O旋转得到△OCD,∴OB=OD,
∴∠BDE=∠OBD=(180°-x°),
∴∠DBE=∠OBD-∠ABO=(180°-x°)-30°,
∠BED=∠ABO+∠BOD=30°+x°.
△BDE是等腰三角形,分三种情况讨论:
①当∠BDE=∠DBE时,(180°-x°)=(180°-x°)-30°,无解;
②当∠BDE=∠BED时,(180°-x°)=30°+x°,解得x=40;
③当∠DBE=∠BED时,
(180°-x°)-30°=30°+x°,解得x=20.
综上所述,当x为20或40时,△BDE是等腰三角形.
练素养
12.【解析】(1)①∵△ABC为等边三角形,
∴BA=BC,∠ABC=60°.
∵△BAO绕点B顺时针旋转后得到△BCD,
∴∠OBD=∠ABC=60°,
∴旋转角的度数为60°.
②∵△BAO绕点B顺时针旋转后得到△BCD,
∴BO=BD,而∠OBD=60°,
∴△OBD为等边三角形,∴OD=OB=4.
③∵△BOD为等边三角形,∴∠BDO=60°.
∵△BAO绕点B顺时针旋转后得到△BCD,
∴CD=AO=3.
在△OCD中,CD=3,OD=4,OC=5,
∵32+42=52,∴CD2+OD2=OC2,
∴△OCD为直角三角形,∠ODC=90°,
∴∠BDC=∠BDO+∠ODC=60°+90°=150°.
(2)当OA2+2OB2=OC2时,∠ODC=90°.
理由如下:
∵△BAO绕点B顺时针旋转后得到△BCD,
∴∠OBD=∠ABC=90°,BO=BD,CD=AO,
∴△OBD为等腰直角三角形,
∴OD=OB.
∵当CD2+OD2=OC2时,△OCD为直角三角形,∠ODC=90°,
∴OA2+2OB2=OC2,
∴当OA,OB,OC满足OA2+2OB2=OC2时,∠ODC=90°.
2
同课章节目录
