23.2.1 中心对称 分层练习 (含答案)2023-2024学年数学人教版九年级上册
文档属性
| 名称 | 23.2.1 中心对称 分层练习 (含答案)2023-2024学年数学人教版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 275.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 15:12:37 | ||
图片预览

文档简介
23.2.1 中心对称
【练基础】
必备知识1 中心对称的定义
1.已知下列命题,其中正确的个数是 ( )
(1)关于中心对称的两个图形可能全等;
(2)关于中心对称的两个图形的对应角相等;
(3)两个全等的三角形一定关于中心对称.
A.0个 B.1个 C.2个 D.3个
2.下列各组图形中,△A'B'C'与△ABC成中心对称的是 ( )
A B
C D
3.下列说法中,正确的个数是 ( )
①线段两端点关于它的中点对称;
②菱形一组对边关于对角线交点对称;
③成中心对称的两个图形一定全等;
④如果两个图形全等,那么这两个图形一定关于某点成中心对称;
⑤如果两个三角形的对应点连线都经过一点,那么这两个三角形成中心对称.
A.2个 B.3个 C.4个 D.5个
必备知识2 中心对称的性质
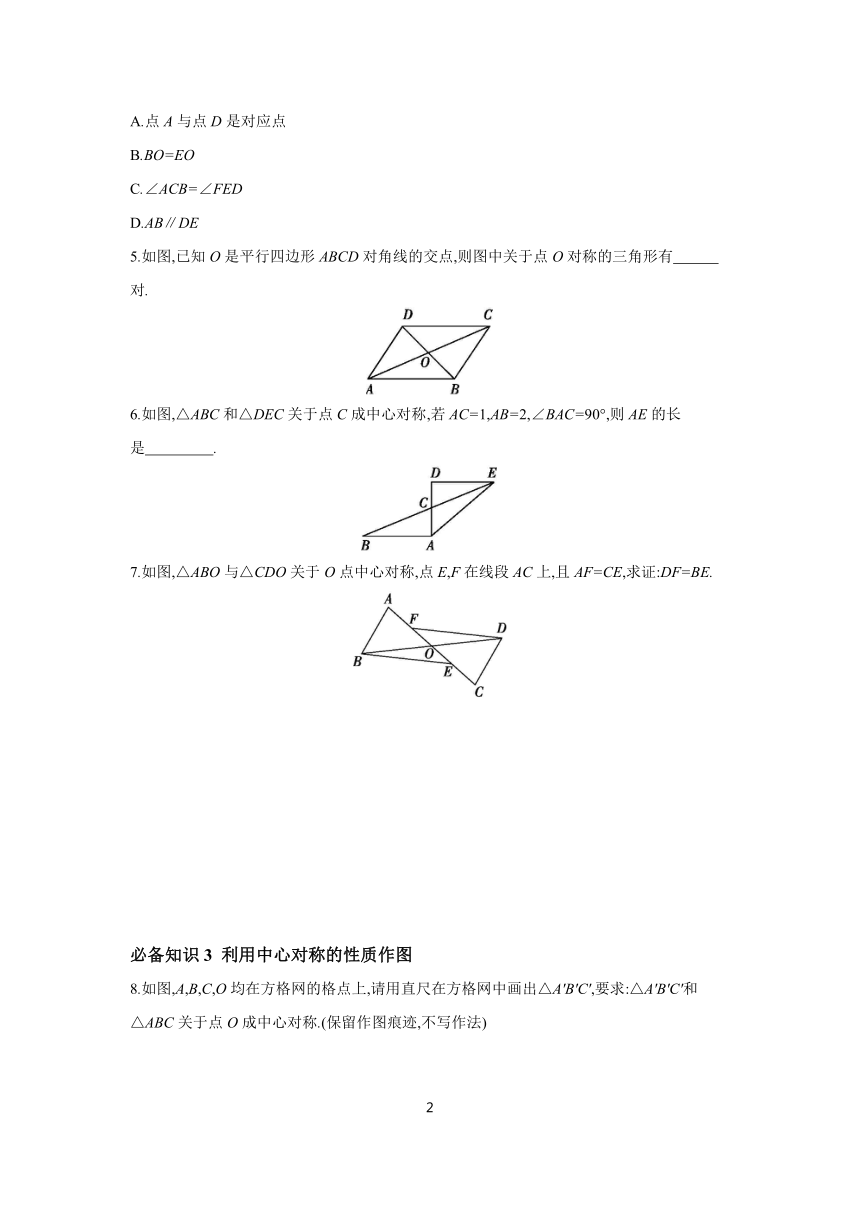
4.如图,△DEF是由△ABC绕点O旋转180°得到的,则下列结论不成立的是 ( )
A.点A与点D是对应点
B.BO=EO
C.∠ACB=∠FED
D.AB∥DE
5.如图,已知O是平行四边形ABCD对角线的交点,则图中关于点O对称的三角形有 对.
6.如图,△ABC和△DEC关于点C成中心对称,若AC=1,AB=2,∠BAC=90°,则AE的长是 .
7.如图,△ABO与△CDO关于O点中心对称,点E,F在线段AC上,且AF=CE,求证:DF=BE.
必备知识3 利用中心对称的性质作图
8.如图,A,B,C,O均在方格网的格点上,请用直尺在方格网中画出△A'B'C',要求:△A'B'C'和△ABC关于点O成中心对称.(保留作图痕迹,不写作法)
【练能力】
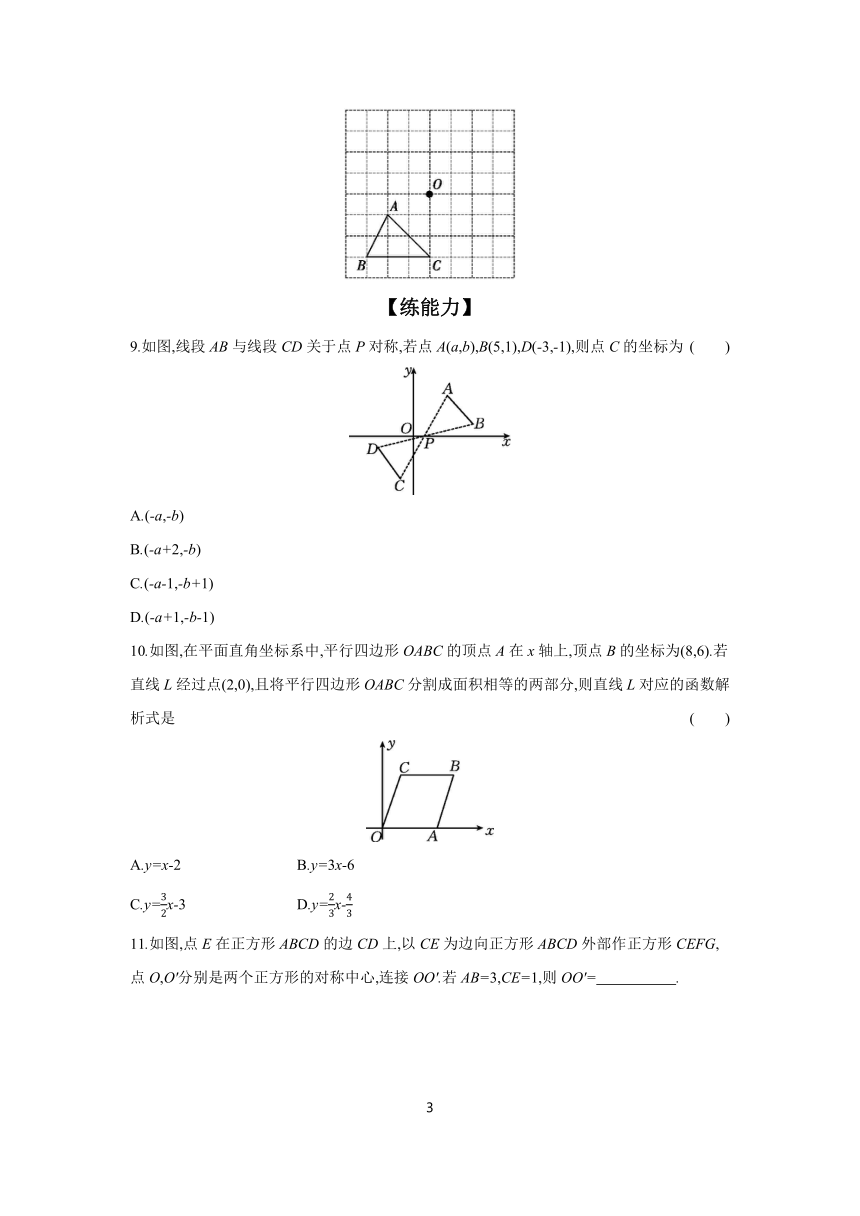
9.如图,线段AB与线段CD关于点P对称,若点A(a,b),B(5,1),D(-3,-1),则点C的坐标为 ( )
A.(-a,-b)
B.(-a+2,-b)
C.(-a-1,-b+1)
D.(-a+1,-b-1)
10.如图,在平面直角坐标系中,平行四边形OABC的顶点A在x轴上,顶点B的坐标为(8,6).若直线L经过点(2,0),且将平行四边形OABC分割成面积相等的两部分,则直线L对应的函数解析式是 ( )
A.y=x-2 B.y=3x-6
C.y=x-3 D.y=x-
11.如图,点E在正方形ABCD的边CD上,以CE为边向正方形ABCD外部作正方形CEFG,点O,O'分别是两个正方形的对称中心,连接OO'.若AB=3,CE=1,则OO'= .
12.如图,A,B为x轴上的两点,以AB为边作矩形ABCD,且A,C的坐标分别为(-8,0),(-2,4),现将矩形ABCD向右平移4个单位长度后,再向上平移个单位长度得到矩形EFGH.
(1)若a=4,请求出点H的坐标.
(2)若将矩形ABCD与矩形EFGH理解为关于点P中心对称,且点P的坐标为(-3,m),求m的值.
【练素养】
13.如图,△ABM与△ACM关于直线AF成轴对称,△ABE与△DCE关于点E成中心对称,点E,D,M都在线段AF上,BM的延长线交CF于点P.
(1)求证:AC=CD.
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
参考答案
练基础
1.B 2.D 3.B 4.C 5.4 6.2
7.【解析】∵△ABO与△CDO关于O点中心对称,∴BO=DO,AO=CO.
∵AF=CE,∴AO-AF=CO-CE,∴FO=EO.
在△FOD和△EOB中,
∴△FOD≌△EOB(SAS),∴DF=BE.
8.【解析】如图,△A'B'C'即所求.
练能力
9.B 【解析】∵线段AB与线段CD关于点P对称,
∴P为线段AC,BD的中点,设C(m,n),
∴=,=,
∴m=2-a,n=-b,
∴C(2-a,-b),故选B.
10.C 11.
12.【解析】(1)∵点A(-8,0)向右平移4个单位长度后,再向上平移==2个单位长度得到点E,
∴点E的坐标为(-4,2).
∵点C(-2,4)向右平移4个单位长度后,再向上平移==2个单位长度得到点G,
∴点G的坐标为(2,6),
∴点H的坐标为(-4,6).
(2)如图,连接AG,DF,它们的交点为P.
由题意有A(-8,0),G2,4+,
∴AG的中点P的坐标为-3,2+.
∵点P的坐标为(-3,m),∴m=2+=.
练素养
13.【解析】(1)证明:∵△ABM与△ACM关于直线AF成轴对称,∴△ABM≌△ACM,∴AB=AC.
又∵△ABE与△DCE关于点E成中心对称,
∴△ABE≌△DCE,∴AB=CD,∴AC=CD.
(2)∠F=∠MCD.
理由:由(1)可得∠BAE=∠CAE=∠CDE,∠CMA=∠BMA,
∵∠BAC=2∠MPC,∠BMA=∠PMF,
∴设∠MPC=α,则∠BAE=∠CAE=∠CDE=α,
设∠BMA=β,则∠PMF=∠CMA=β,
∴∠F=∠CPM-∠PMF=α-β,
∠MCD=∠CDE-∠DMC=α-β,
∴∠F=∠MCD.
2
【练基础】
必备知识1 中心对称的定义
1.已知下列命题,其中正确的个数是 ( )
(1)关于中心对称的两个图形可能全等;
(2)关于中心对称的两个图形的对应角相等;
(3)两个全等的三角形一定关于中心对称.
A.0个 B.1个 C.2个 D.3个
2.下列各组图形中,△A'B'C'与△ABC成中心对称的是 ( )
A B
C D
3.下列说法中,正确的个数是 ( )
①线段两端点关于它的中点对称;
②菱形一组对边关于对角线交点对称;
③成中心对称的两个图形一定全等;
④如果两个图形全等,那么这两个图形一定关于某点成中心对称;
⑤如果两个三角形的对应点连线都经过一点,那么这两个三角形成中心对称.
A.2个 B.3个 C.4个 D.5个
必备知识2 中心对称的性质
4.如图,△DEF是由△ABC绕点O旋转180°得到的,则下列结论不成立的是 ( )
A.点A与点D是对应点
B.BO=EO
C.∠ACB=∠FED
D.AB∥DE
5.如图,已知O是平行四边形ABCD对角线的交点,则图中关于点O对称的三角形有 对.
6.如图,△ABC和△DEC关于点C成中心对称,若AC=1,AB=2,∠BAC=90°,则AE的长是 .
7.如图,△ABO与△CDO关于O点中心对称,点E,F在线段AC上,且AF=CE,求证:DF=BE.
必备知识3 利用中心对称的性质作图
8.如图,A,B,C,O均在方格网的格点上,请用直尺在方格网中画出△A'B'C',要求:△A'B'C'和△ABC关于点O成中心对称.(保留作图痕迹,不写作法)
【练能力】
9.如图,线段AB与线段CD关于点P对称,若点A(a,b),B(5,1),D(-3,-1),则点C的坐标为 ( )
A.(-a,-b)
B.(-a+2,-b)
C.(-a-1,-b+1)
D.(-a+1,-b-1)
10.如图,在平面直角坐标系中,平行四边形OABC的顶点A在x轴上,顶点B的坐标为(8,6).若直线L经过点(2,0),且将平行四边形OABC分割成面积相等的两部分,则直线L对应的函数解析式是 ( )
A.y=x-2 B.y=3x-6
C.y=x-3 D.y=x-
11.如图,点E在正方形ABCD的边CD上,以CE为边向正方形ABCD外部作正方形CEFG,点O,O'分别是两个正方形的对称中心,连接OO'.若AB=3,CE=1,则OO'= .
12.如图,A,B为x轴上的两点,以AB为边作矩形ABCD,且A,C的坐标分别为(-8,0),(-2,4),现将矩形ABCD向右平移4个单位长度后,再向上平移个单位长度得到矩形EFGH.
(1)若a=4,请求出点H的坐标.
(2)若将矩形ABCD与矩形EFGH理解为关于点P中心对称,且点P的坐标为(-3,m),求m的值.
【练素养】
13.如图,△ABM与△ACM关于直线AF成轴对称,△ABE与△DCE关于点E成中心对称,点E,D,M都在线段AF上,BM的延长线交CF于点P.
(1)求证:AC=CD.
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
参考答案
练基础
1.B 2.D 3.B 4.C 5.4 6.2
7.【解析】∵△ABO与△CDO关于O点中心对称,∴BO=DO,AO=CO.
∵AF=CE,∴AO-AF=CO-CE,∴FO=EO.
在△FOD和△EOB中,
∴△FOD≌△EOB(SAS),∴DF=BE.
8.【解析】如图,△A'B'C'即所求.
练能力
9.B 【解析】∵线段AB与线段CD关于点P对称,
∴P为线段AC,BD的中点,设C(m,n),
∴=,=,
∴m=2-a,n=-b,
∴C(2-a,-b),故选B.
10.C 11.
12.【解析】(1)∵点A(-8,0)向右平移4个单位长度后,再向上平移==2个单位长度得到点E,
∴点E的坐标为(-4,2).
∵点C(-2,4)向右平移4个单位长度后,再向上平移==2个单位长度得到点G,
∴点G的坐标为(2,6),
∴点H的坐标为(-4,6).
(2)如图,连接AG,DF,它们的交点为P.
由题意有A(-8,0),G2,4+,
∴AG的中点P的坐标为-3,2+.
∵点P的坐标为(-3,m),∴m=2+=.
练素养
13.【解析】(1)证明:∵△ABM与△ACM关于直线AF成轴对称,∴△ABM≌△ACM,∴AB=AC.
又∵△ABE与△DCE关于点E成中心对称,
∴△ABE≌△DCE,∴AB=CD,∴AC=CD.
(2)∠F=∠MCD.
理由:由(1)可得∠BAE=∠CAE=∠CDE,∠CMA=∠BMA,
∵∠BAC=2∠MPC,∠BMA=∠PMF,
∴设∠MPC=α,则∠BAE=∠CAE=∠CDE=α,
设∠BMA=β,则∠PMF=∠CMA=β,
∴∠F=∠CPM-∠PMF=α-β,
∠MCD=∠CDE-∠DMC=α-β,
∴∠F=∠MCD.
2
同课章节目录
