2023-2024学年数学人教版九年级上册23.2.2 中心对称图形 分层练习(含答案)
文档属性
| 名称 | 2023-2024学年数学人教版九年级上册23.2.2 中心对称图形 分层练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 349.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 15:13:27 | ||
图片预览

文档简介
23.2.2 中心对称图形
【练基础】
必备知识1 中心对称图形
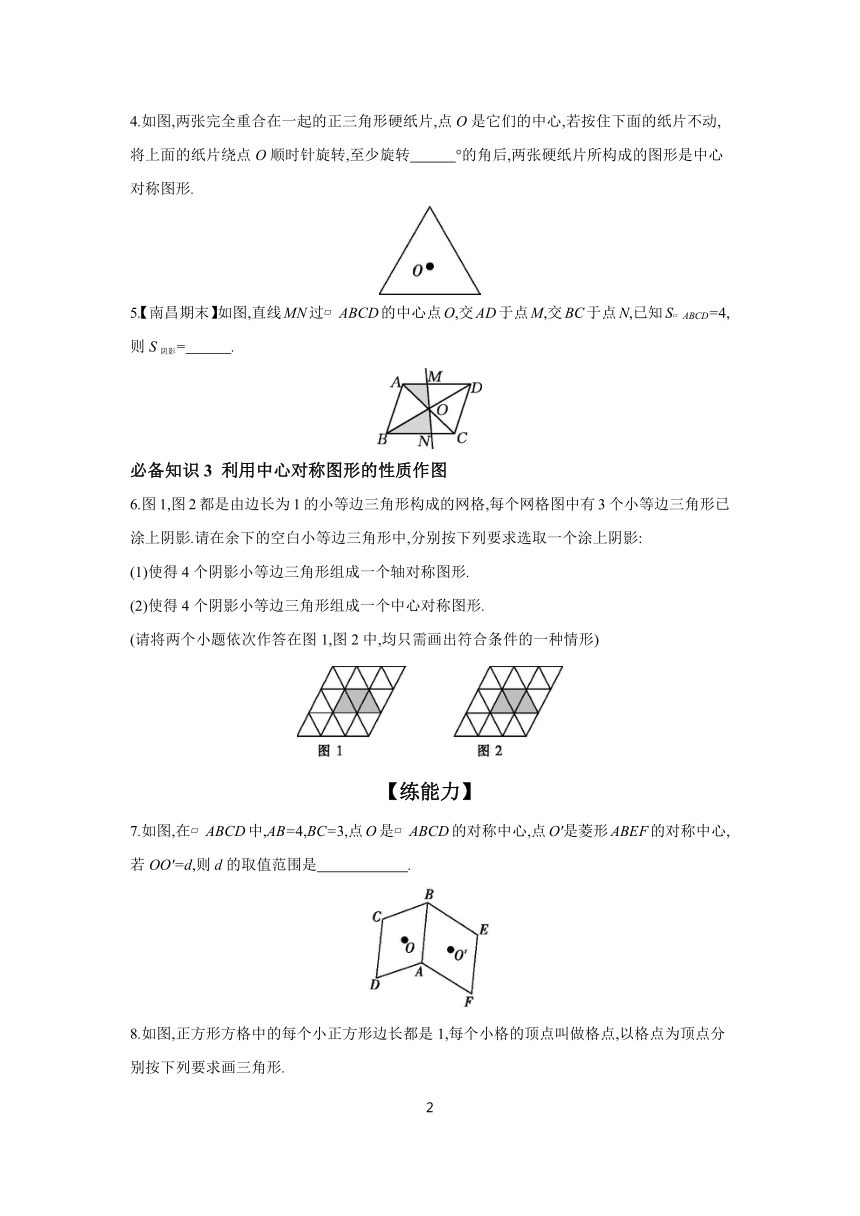
1.《国家宝藏》节目立足于中华文化宝库资源,通过对文物的梳理与总结,演绎文物背后的故事与历史让更多的观众走进博物馆,让一个个馆藏文物鲜活起来,如图,这四幅图是我国一些博物馆的标志,其中是中心对称图形的是 ( )
A B
C D
2.下列四幅图片上呈现的是垃圾类型及标识图案,其中标识图案是中心对称图形的是 ( )
A B C D
3.没有哪一门学科能像数学这样,利用如此多的符号图形,展现一系列完备且完美的世界.下面是由4个数学式子绘制成的完美曲线,其中是中心对称图形的是 ( )
A.笛卡尔心形线 B.f三叶玫瑰形曲线
C.蝴蝶形曲线 D.(s)太极曲线
必备知识2 中心对称图形的性质
4.如图,两张完全重合在一起的正三角形硬纸片,点O是它们的中心,若按住下面的纸片不动,将上面的纸片绕点O顺时针旋转,至少旋转 °的角后,两张硬纸片所构成的图形是中心对称图形.
5.【南昌期末】如图,直线MN过 ABCD的中心点O,交AD于点M,交BC于点N,已知S ABCD=4,则S阴影= .
必备知识3 利用中心对称图形的性质作图
6.图1,图2都是由边长为1的小等边三角形构成的网格,每个网格图中有3个小等边三角形已涂上阴影.请在余下的空白小等边三角形中,分别按下列要求选取一个涂上阴影:
(1)使得4个阴影小等边三角形组成一个轴对称图形.
(2)使得4个阴影小等边三角形组成一个中心对称图形.
(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
【练能力】
7.如图,在 ABCD中,AB=4,BC=3,点O是 ABCD的对称中心,点O'是菱形ABEF的对称中心,若OO'=d,则d的取值范围是 .
8.如图,正方形方格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图1中,画出一个三角形,使它的三边长都是无理数,并作出该三角形的一个中心对称图形.
(2)在图2中,画出一个直角三角形,使它的三边长都是整数,并通过旋转或轴对称等作出一个中心对称图形.
(3)在图3中,画出一个中心对称图形.
【练素养】
9.图1,图2,图3的网格均由边长为1的小正方形组成,图1是三国时期吴国的数学家赵爽所绘制的“弦图”,它由四个形状、大小完全相同的直角三角形组成,赵爽利用这个“弦图”对勾股定理作出了证明,是中国古代数学的一项重要成就,请根据下列要求解答问题.
(1)图1中的“弦图”的四个直角三角形组成的图形是 对称图形.(填“轴”或“中心”)
(2)请将“弦图”中的四个直角三角形通过你所学过的图形变换,在图2,图3的网格纸中设计另外两个不同的图案,画图要求:
①每个直角三角形的顶点均在网格纸的格点上,且四个三角形互不重叠,不必涂阴影;
②图2中所设计的图案(不含方格纸)必须是轴对称图形而不是中心对称图形,图3中所设计的图案(不含方格纸)必须既是轴对称图形,又是中心对称图形.
参考答案
练基础
1.A 2.D 3.D 4.60 5.1
6.【解析】(1)轴对称图形如图1所示.
(2)中心对称图形如图2所示.
练能力
7.0.5≤d≤3.5
8.【解析】(1)答案不唯一,如三边长分别为2、、如图1.
(2)答案不唯一,如三边长分别为3、4、5,如图2.
(3)答案不唯一,如画一个平行四边形,如图3.
9.【解析】(1)中心.
(2)图1是轴对称图形而不是中心对称图形.
图2既是轴对称图形,又是中心对称图形.
2
【练基础】
必备知识1 中心对称图形
1.《国家宝藏》节目立足于中华文化宝库资源,通过对文物的梳理与总结,演绎文物背后的故事与历史让更多的观众走进博物馆,让一个个馆藏文物鲜活起来,如图,这四幅图是我国一些博物馆的标志,其中是中心对称图形的是 ( )
A B
C D
2.下列四幅图片上呈现的是垃圾类型及标识图案,其中标识图案是中心对称图形的是 ( )
A B C D
3.没有哪一门学科能像数学这样,利用如此多的符号图形,展现一系列完备且完美的世界.下面是由4个数学式子绘制成的完美曲线,其中是中心对称图形的是 ( )
A.笛卡尔心形线 B.f三叶玫瑰形曲线
C.蝴蝶形曲线 D.(s)太极曲线
必备知识2 中心对称图形的性质
4.如图,两张完全重合在一起的正三角形硬纸片,点O是它们的中心,若按住下面的纸片不动,将上面的纸片绕点O顺时针旋转,至少旋转 °的角后,两张硬纸片所构成的图形是中心对称图形.
5.【南昌期末】如图,直线MN过 ABCD的中心点O,交AD于点M,交BC于点N,已知S ABCD=4,则S阴影= .
必备知识3 利用中心对称图形的性质作图
6.图1,图2都是由边长为1的小等边三角形构成的网格,每个网格图中有3个小等边三角形已涂上阴影.请在余下的空白小等边三角形中,分别按下列要求选取一个涂上阴影:
(1)使得4个阴影小等边三角形组成一个轴对称图形.
(2)使得4个阴影小等边三角形组成一个中心对称图形.
(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
【练能力】
7.如图,在 ABCD中,AB=4,BC=3,点O是 ABCD的对称中心,点O'是菱形ABEF的对称中心,若OO'=d,则d的取值范围是 .
8.如图,正方形方格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图1中,画出一个三角形,使它的三边长都是无理数,并作出该三角形的一个中心对称图形.
(2)在图2中,画出一个直角三角形,使它的三边长都是整数,并通过旋转或轴对称等作出一个中心对称图形.
(3)在图3中,画出一个中心对称图形.
【练素养】
9.图1,图2,图3的网格均由边长为1的小正方形组成,图1是三国时期吴国的数学家赵爽所绘制的“弦图”,它由四个形状、大小完全相同的直角三角形组成,赵爽利用这个“弦图”对勾股定理作出了证明,是中国古代数学的一项重要成就,请根据下列要求解答问题.
(1)图1中的“弦图”的四个直角三角形组成的图形是 对称图形.(填“轴”或“中心”)
(2)请将“弦图”中的四个直角三角形通过你所学过的图形变换,在图2,图3的网格纸中设计另外两个不同的图案,画图要求:
①每个直角三角形的顶点均在网格纸的格点上,且四个三角形互不重叠,不必涂阴影;
②图2中所设计的图案(不含方格纸)必须是轴对称图形而不是中心对称图形,图3中所设计的图案(不含方格纸)必须既是轴对称图形,又是中心对称图形.
参考答案
练基础
1.A 2.D 3.D 4.60 5.1
6.【解析】(1)轴对称图形如图1所示.
(2)中心对称图形如图2所示.
练能力
7.0.5≤d≤3.5
8.【解析】(1)答案不唯一,如三边长分别为2、、如图1.
(2)答案不唯一,如三边长分别为3、4、5,如图2.
(3)答案不唯一,如画一个平行四边形,如图3.
9.【解析】(1)中心.
(2)图1是轴对称图形而不是中心对称图形.
图2既是轴对称图形,又是中心对称图形.
2
同课章节目录
