23.2.3 关于原点对称的点的坐标 分层练习(含答案) 2023-2024学年数学人教版九年级上册
文档属性
| 名称 | 23.2.3 关于原点对称的点的坐标 分层练习(含答案) 2023-2024学年数学人教版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 346.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 15:13:54 | ||
图片预览


文档简介
23.2.3 关于原点对称的点的坐标
【练基础】
必备知识1 关于原点对称的点的坐标
1.【2022·唐山期末】在平面直角坐标系中,点A(-2,4)与点A'关于原点对称,则点A'的坐标是 ( )
A.(-2,-4) B.(2,4)
C.(-2,4) D.(2,-4)
2.“小马虎”在做作业时,将点A横、纵坐标的顺序颠倒了,误为A(-b,a),“小糊涂”也不细心,将点B的坐标写成其关于x轴对称的点的坐标,误为B(-a,-b),则A、B两点原来的位置关系是 ( )
A.关于x轴对称 B.关于原点对称
C.关于y轴对称 D.重合
3.【2023·保定月考】已知点A(-1,-2)与点B( ,2)关于点P(2,0)对称,则 指的是 ( )
A.1 B.3 C.5 D.2
4.点A(-4,3)关于原点O对称的点为B,则线段AB的长为 .
5.已知点M(a,-3)和点N(4,b)关于原点对称,则(a+b)2027= .
6.已知点P(2x,y2+4)与点Q(x2+1,-4y)关于原点对称,求x+y的值.
必备知识2 利用关于原点对称的点的坐标作图
7.已知点A(-1,3a-1)与点B(2b+1,-2)关于x轴对称,点C(a+2,b)与点D关于原点对称.
(1)求点A,B,C,D的坐标.
(2)顺次连接点A,D,B,C,求所得图形的面积.
8.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)将△ABC先向右平移4个单位长度,再向下平移5个单位长度,得到△A1B1C1,画出△A1B1C1,并写出点B对应的点B1的坐标.
(2)将△ABC绕着点O按逆时针方向旋转90°得到△A2B2C2,画出△A2B2C2.
【练能力】
9.若点P(a+1,a-2)关于原点对称的点位于第二象限,则a的取值范围表示正确的是 ( )
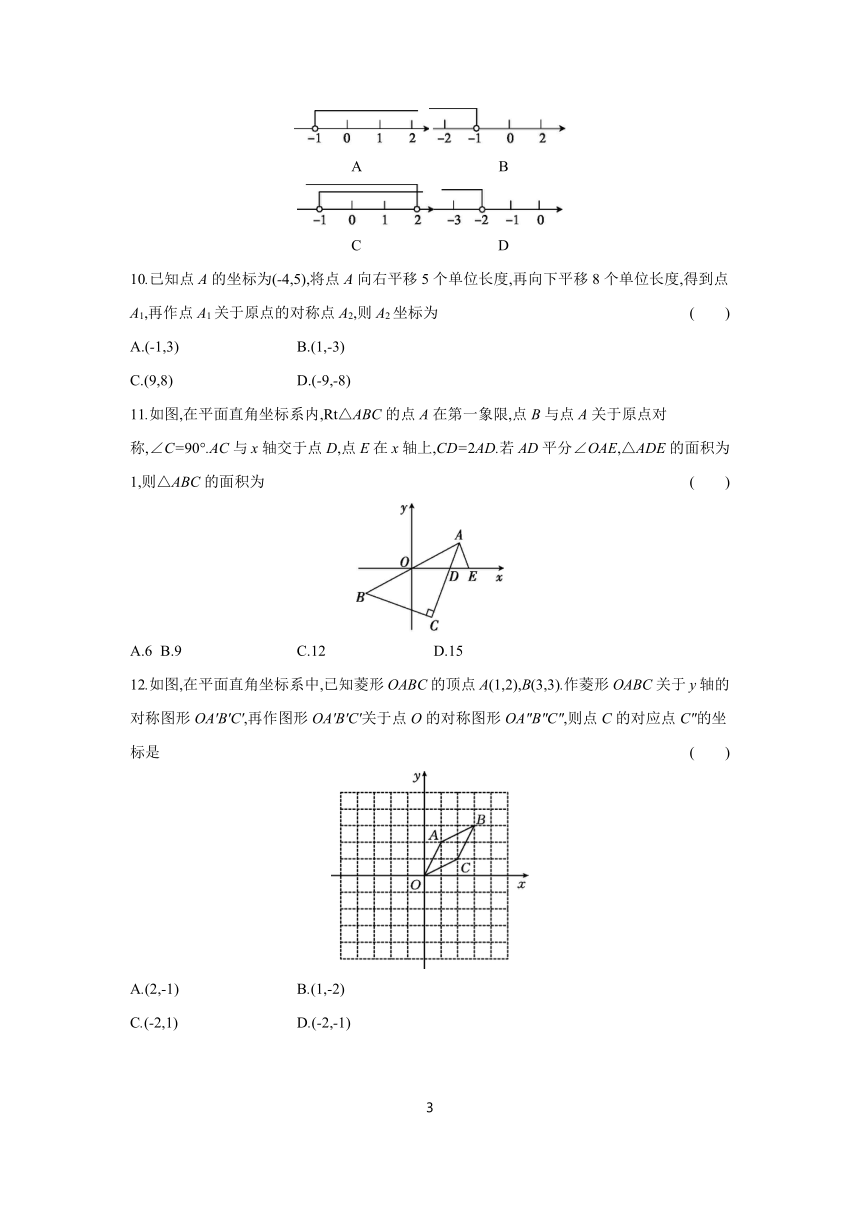
A B
C D
10.已知点A的坐标为(-4,5),将点A向右平移5个单位长度,再向下平移8个单位长度,得到点A1,再作点A1关于原点的对称点A2,则A2坐标为 ( )
A.(-1,3) B.(1,-3)
C.(9,8) D.(-9,-8)
11.如图,在平面直角坐标系内,Rt△ABC的点A在第一象限,点B与点A关于原点对称,∠C=90°.AC与x轴交于点D,点E在x轴上,CD=2AD.若AD平分∠OAE,△ADE的面积为1,则△ABC的面积为 ( )
A.6 B.9 C.12 D.15
12.如图,在平面直角坐标系中,已知菱形OABC的顶点A(1,2),B(3,3).作菱形OABC关于y轴的对称图形OA'B'C',再作图形OA'B'C'关于点O的对称图形OA″B″C″,则点C的对应点C″的坐标是 ( )
A.(2,-1) B.(1,-2)
C.(-2,1) D.(-2,-1)
13.在平面直角坐标系中,已知点A(3,2),作点A关于y轴的对称点A1,点A1关于原点的对称点A2,点A2关于x轴的对称点A3,A3关于y轴的对称点A4,…,按此规律,则点A2027的坐标为 .
14.在平面直角坐标系中,对于平面内任一点(a,b),若规定以下三种变换:
①f(a,b)=(-b,-a),如f(1,3)=(-3,-1);
②g(a,b)=(b,a),如g(1,3)=(3,1);
③h(a,b)=(-a,b),如h(1,3)=(-1,3).
且规定了运算顺序是“由内到外”,例如按照以上规定有:f(g(2,-3))=f(-3,2)=(-2,3),那么f(g(h(5,-3)))= .
15.已知点P(x2+2x,3)在第二象限,且与点Q(x+2,y)关于原点对称,试求x+2y的值.
16.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,5),B(-4,2),C(-2,2).
(1)平移△ABC,使点B移动到点B1(1,1),画出平移后的△A1B1C1,并写出点A1,C1的坐标.
(2)画出△ABC关于原点O对称的△A2B2C2.
(3)线段AA1的长度为 .
参考答案
练基础
1.D 2.B 3.C 4.10 5.-1
6.【解析】∵点P(2x,y2+4)与点Q(x2+1,-4y)关于原点对称,
∴x2+1+2x=0,y2+4-4y=0,
∴(x+1)2=0,(y-2)2=0,
∴x=-1,y=2,∴x+y=1.
7.【解析】(1)∵点A(-1,3a-1)与点B(2b+1,-2)关于x轴对称,
∴2b+1=-1,3a-1=2,
解得a=1,b=-1,
∴点A(-1,2),B(-1,-2),C(3,-1).
∵点C(a+2,b)与点D关于原点对称,
∴点D(-3,1).
(2)如图所示:
四边形ADBC的面积为×4×2+×4×4=12.
8.【解析】(1)如图,△A1B1C1即所求,点B1的坐标为(2,-4).
(2)如图,△A2B2C2即所求.
练能力
9.C 10.A 11.C 12.A 13.(3,-2) 14.(5,3)
15.【解析】根据题意,得(x2+2x)+(x+2)=0,y=-3.
解方程(x2+2x)+(x+2)=0,得x1=-1,x2=-2.
当x=-1时,x2+2x=-1,点P(-1,3)在第二象限,符合题意.
当x=-2时,x2+2x=0,与点P在第二象限矛盾,不符合题意,舍去.
∴x=-1,y=-3,∴x+2y=-7.
16.【解析】(1)△A1B1C1如图所示,A1(4,4),C1(3,1).
(2)△A2B2C2如图所示.
(3).
2
【练基础】
必备知识1 关于原点对称的点的坐标
1.【2022·唐山期末】在平面直角坐标系中,点A(-2,4)与点A'关于原点对称,则点A'的坐标是 ( )
A.(-2,-4) B.(2,4)
C.(-2,4) D.(2,-4)
2.“小马虎”在做作业时,将点A横、纵坐标的顺序颠倒了,误为A(-b,a),“小糊涂”也不细心,将点B的坐标写成其关于x轴对称的点的坐标,误为B(-a,-b),则A、B两点原来的位置关系是 ( )
A.关于x轴对称 B.关于原点对称
C.关于y轴对称 D.重合
3.【2023·保定月考】已知点A(-1,-2)与点B( ,2)关于点P(2,0)对称,则 指的是 ( )
A.1 B.3 C.5 D.2
4.点A(-4,3)关于原点O对称的点为B,则线段AB的长为 .
5.已知点M(a,-3)和点N(4,b)关于原点对称,则(a+b)2027= .
6.已知点P(2x,y2+4)与点Q(x2+1,-4y)关于原点对称,求x+y的值.
必备知识2 利用关于原点对称的点的坐标作图
7.已知点A(-1,3a-1)与点B(2b+1,-2)关于x轴对称,点C(a+2,b)与点D关于原点对称.
(1)求点A,B,C,D的坐标.
(2)顺次连接点A,D,B,C,求所得图形的面积.
8.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)将△ABC先向右平移4个单位长度,再向下平移5个单位长度,得到△A1B1C1,画出△A1B1C1,并写出点B对应的点B1的坐标.
(2)将△ABC绕着点O按逆时针方向旋转90°得到△A2B2C2,画出△A2B2C2.
【练能力】
9.若点P(a+1,a-2)关于原点对称的点位于第二象限,则a的取值范围表示正确的是 ( )
A B
C D
10.已知点A的坐标为(-4,5),将点A向右平移5个单位长度,再向下平移8个单位长度,得到点A1,再作点A1关于原点的对称点A2,则A2坐标为 ( )
A.(-1,3) B.(1,-3)
C.(9,8) D.(-9,-8)
11.如图,在平面直角坐标系内,Rt△ABC的点A在第一象限,点B与点A关于原点对称,∠C=90°.AC与x轴交于点D,点E在x轴上,CD=2AD.若AD平分∠OAE,△ADE的面积为1,则△ABC的面积为 ( )
A.6 B.9 C.12 D.15
12.如图,在平面直角坐标系中,已知菱形OABC的顶点A(1,2),B(3,3).作菱形OABC关于y轴的对称图形OA'B'C',再作图形OA'B'C'关于点O的对称图形OA″B″C″,则点C的对应点C″的坐标是 ( )
A.(2,-1) B.(1,-2)
C.(-2,1) D.(-2,-1)
13.在平面直角坐标系中,已知点A(3,2),作点A关于y轴的对称点A1,点A1关于原点的对称点A2,点A2关于x轴的对称点A3,A3关于y轴的对称点A4,…,按此规律,则点A2027的坐标为 .
14.在平面直角坐标系中,对于平面内任一点(a,b),若规定以下三种变换:
①f(a,b)=(-b,-a),如f(1,3)=(-3,-1);
②g(a,b)=(b,a),如g(1,3)=(3,1);
③h(a,b)=(-a,b),如h(1,3)=(-1,3).
且规定了运算顺序是“由内到外”,例如按照以上规定有:f(g(2,-3))=f(-3,2)=(-2,3),那么f(g(h(5,-3)))= .
15.已知点P(x2+2x,3)在第二象限,且与点Q(x+2,y)关于原点对称,试求x+2y的值.
16.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,5),B(-4,2),C(-2,2).
(1)平移△ABC,使点B移动到点B1(1,1),画出平移后的△A1B1C1,并写出点A1,C1的坐标.
(2)画出△ABC关于原点O对称的△A2B2C2.
(3)线段AA1的长度为 .
参考答案
练基础
1.D 2.B 3.C 4.10 5.-1
6.【解析】∵点P(2x,y2+4)与点Q(x2+1,-4y)关于原点对称,
∴x2+1+2x=0,y2+4-4y=0,
∴(x+1)2=0,(y-2)2=0,
∴x=-1,y=2,∴x+y=1.
7.【解析】(1)∵点A(-1,3a-1)与点B(2b+1,-2)关于x轴对称,
∴2b+1=-1,3a-1=2,
解得a=1,b=-1,
∴点A(-1,2),B(-1,-2),C(3,-1).
∵点C(a+2,b)与点D关于原点对称,
∴点D(-3,1).
(2)如图所示:
四边形ADBC的面积为×4×2+×4×4=12.
8.【解析】(1)如图,△A1B1C1即所求,点B1的坐标为(2,-4).
(2)如图,△A2B2C2即所求.
练能力
9.C 10.A 11.C 12.A 13.(3,-2) 14.(5,3)
15.【解析】根据题意,得(x2+2x)+(x+2)=0,y=-3.
解方程(x2+2x)+(x+2)=0,得x1=-1,x2=-2.
当x=-1时,x2+2x=-1,点P(-1,3)在第二象限,符合题意.
当x=-2时,x2+2x=0,与点P在第二象限矛盾,不符合题意,舍去.
∴x=-1,y=-3,∴x+2y=-7.
16.【解析】(1)△A1B1C1如图所示,A1(4,4),C1(3,1).
(2)△A2B2C2如图所示.
(3).
2
同课章节目录
