2023-2024学年数学人教版九年级上册24.1.1 圆 分层练习(含解析)
文档属性
| 名称 | 2023-2024学年数学人教版九年级上册24.1.1 圆 分层练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 172.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 15:14:24 | ||
图片预览

文档简介
24.1.1 圆
【练基础】
必备知识1 圆的定义
1.以已知点O为圆心,线段a为半径作圆,可以作 ( )
A.1个 B.2个 C.3个 D.无数个
2.以3 cm为半径画圆,这样的圆有 ( )
A.1个 B.2个 C.3个 D.无数个
3.如图,△ABC和△ABD都为直角三角形,且∠C=∠D=90°.求证:A,B,C,D四点在同一个圆上.
必备知识2 与圆有关的概念
4.等于圆周的弧叫做 ( )
A.劣弧 B.半圆 C.优弧 D.圆
5.下列说法,正确的是 ( )
A.半径相等的两个圆大小相等
B.长度相等的两条弧是等弧
C.直径不一定是圆中最长的弦
D.圆上两点之间的部分叫做弦
6.已知AB是半径为5的圆的一条弦,则AB的长不可能是 ( )
A.4 B.8 C.10 D.12
7.如图,在☉O中,线段 是☉O的半径;线段 是☉O的弦,其中最长的弦是 ; 是劣弧, 是优弧.(将满足要求的答案全部填上)
必备知识3 与圆有关的计算和推理
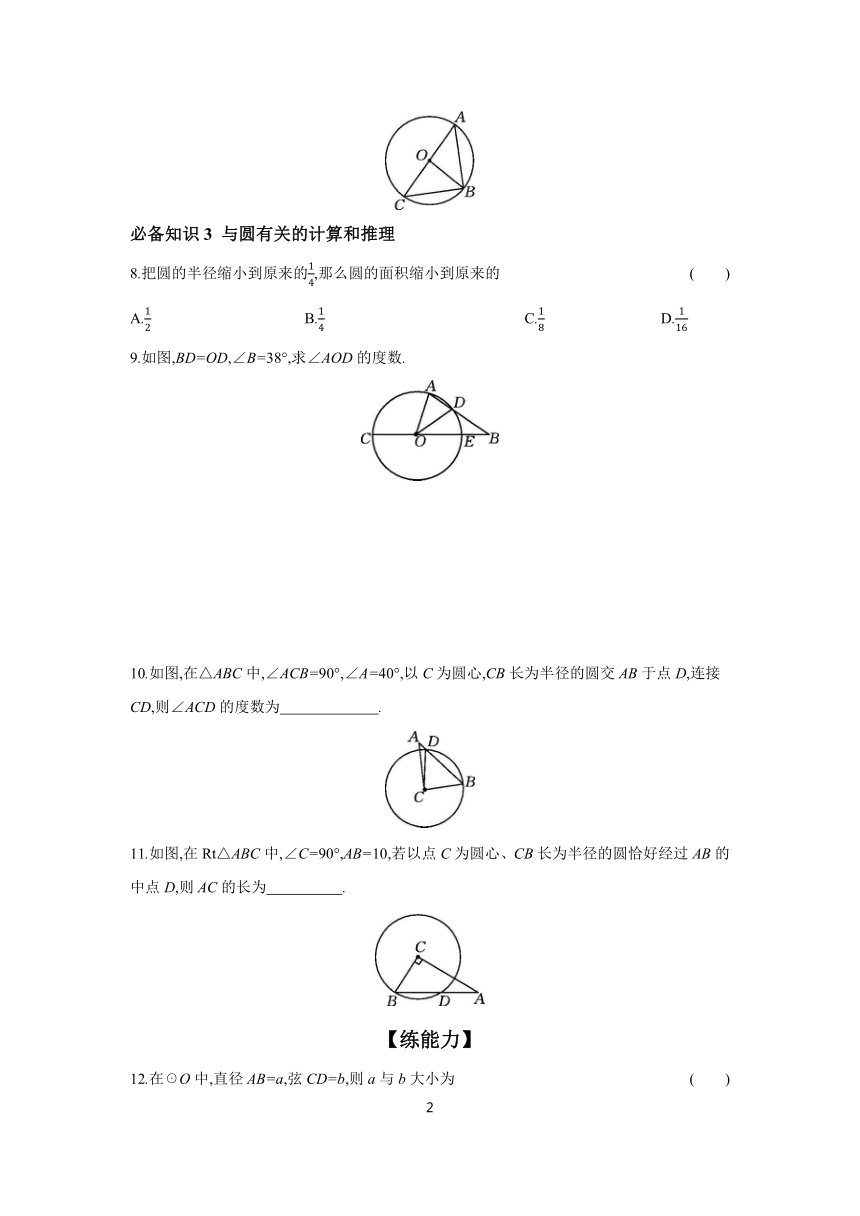
8.把圆的半径缩小到原来的,那么圆的面积缩小到原来的 ( )
A. B. C. D.
9.如图,BD=OD,∠B=38°,求∠AOD的度数.
10.如图,在△ABC中,∠ACB=90°,∠A=40°,以C为圆心,CB长为半径的圆交AB于点D,连接CD,则∠ACD的度数为 .
11.如图,在Rt△ABC中,∠C=90°,AB=10,若以点C为圆心、CB长为半径的圆恰好经过AB的中点D,则AC的长为 .
【练能力】
12.在☉O中,直径AB=a,弦CD=b,则a与b大小为 ( )
A.a>b B.a≥b
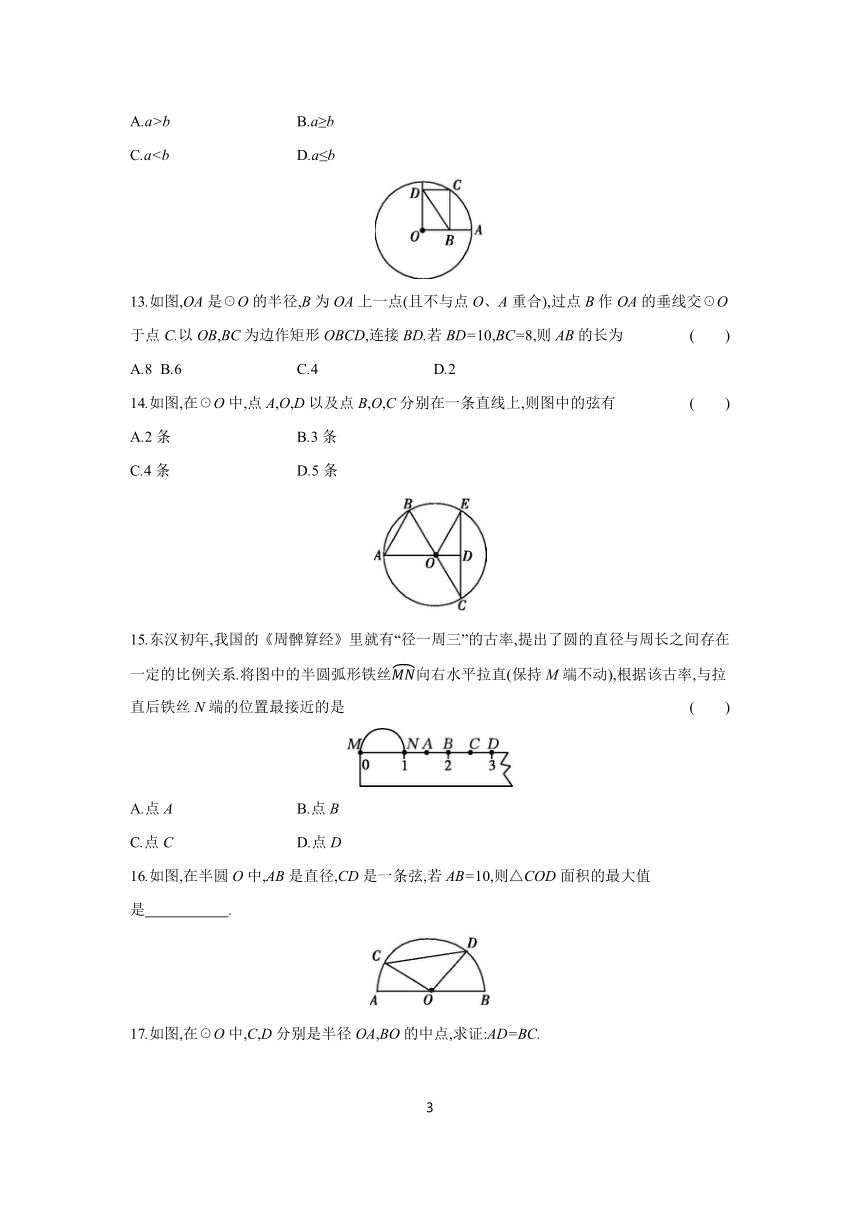
C.a13.如图,OA是☉O的半径,B为OA上一点(且不与点O、A重合),过点B作OA的垂线交☉O于点C.以OB,BC为边作矩形OBCD,连接BD.若BD=10,BC=8,则AB的长为 ( )
A.8 B.6 C.4 D.2
14.如图,在☉O中,点A,O,D以及点B,O,C分别在一条直线上,则图中的弦有 ( )
A.2条 B.3条
C.4条 D.5条
15.东汉初年,我国的《周髀算经》里就有“径一周三”的古率,提出了圆的直径与周长之间存在一定的比例关系.将图中的半圆弧形铁丝向右水平拉直(保持M端不动),根据该古率,与拉直后铁丝N端的位置最接近的是 ( )
A.点A B.点B
C.点C D.点D
16.如图,在半圆O中,AB是直径,CD是一条弦,若AB=10,则△COD面积的最大值是 .
17.如图,在☉O中,C,D分别是半径OA,BO的中点,求证:AD=BC.
18.如图,AB是☉O的直径,CD是☉O的弦,AB,CD的延长线交于点E.已知AB=2DE,∠AEC=25°,求∠AOC的度数.
【练素养】
19.在☉O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在☉O上,且OP⊥PQ.
(1)如图1,当PQ∥AB时,求PQ的长度.
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
参考答案
练基础
1.A 2.D
3.【解析】如图,取AB的中点O,连接OC,OD.
∵△ABC和△ABD都为直角三角形,且∠ACB=∠ADB=90°,
∴DO,CO分别为Rt△ABD和Rt△ABC斜边上的中线,
∴OA=OB=OC=OD,
∴A,B,C,D四点在同一个圆上.
4.C 5.A 6.D
7.【解析】OA,OB,OC;AB,BC,AC;AC;, ,
8.D
9.【解析】∵BD=OD,∠B=38°,
∴∠DOB=∠B=38°,
∴∠ADO=∠DOB+∠B=2×38°=76°.
∵OA=OD,∴∠A=∠ADO=76°,
∴∠AOD=180°-∠A-∠ADO=180°-76°-76°=28°.
10.10° 11.5
练能力
12.B 13.C 14.B 15.A 16.12.5
17.【解析】∵OA,OB是☉O的两条半径,
∴AO=BO.
∵C,D分别是半径OA,BO的中点,
∴OC=OD.
在△ODA和△OCB中,
∴△ODA≌△OCB(SAS),
∴AD=BC.
18.【解析】如图,连接OD.
∵AB=2DE=2OD,
∴OD=DE.
又∵∠E=25°,
∴∠DOE=∠E=25°,
∴∠ODC=50°,
同理∠C=∠ODC=50°.
∴∠AOC=∠E+∠OCE=75°.
练素养
19.【解析】(1)如图1,连接OQ.
∵PQ∥AB,OP⊥PQ.∴OP⊥AB.
在Rt△OBP中,∵OB=AB=3,∠ABC=30°,
∴PB=2OP,由勾股定理可得OP=.
在Rt△OPQ中,PQ===.
(2)如图2,连接OQ,在Rt△OPQ中,PQ==,
∴当OP的长最小时,PQ的长最大.
此时OP⊥BC,则OP=OB=,
∴PQ长的最大值为==.
2
【练基础】
必备知识1 圆的定义
1.以已知点O为圆心,线段a为半径作圆,可以作 ( )
A.1个 B.2个 C.3个 D.无数个
2.以3 cm为半径画圆,这样的圆有 ( )
A.1个 B.2个 C.3个 D.无数个
3.如图,△ABC和△ABD都为直角三角形,且∠C=∠D=90°.求证:A,B,C,D四点在同一个圆上.
必备知识2 与圆有关的概念
4.等于圆周的弧叫做 ( )
A.劣弧 B.半圆 C.优弧 D.圆
5.下列说法,正确的是 ( )
A.半径相等的两个圆大小相等
B.长度相等的两条弧是等弧
C.直径不一定是圆中最长的弦
D.圆上两点之间的部分叫做弦
6.已知AB是半径为5的圆的一条弦,则AB的长不可能是 ( )
A.4 B.8 C.10 D.12
7.如图,在☉O中,线段 是☉O的半径;线段 是☉O的弦,其中最长的弦是 ; 是劣弧, 是优弧.(将满足要求的答案全部填上)
必备知识3 与圆有关的计算和推理
8.把圆的半径缩小到原来的,那么圆的面积缩小到原来的 ( )
A. B. C. D.
9.如图,BD=OD,∠B=38°,求∠AOD的度数.
10.如图,在△ABC中,∠ACB=90°,∠A=40°,以C为圆心,CB长为半径的圆交AB于点D,连接CD,则∠ACD的度数为 .
11.如图,在Rt△ABC中,∠C=90°,AB=10,若以点C为圆心、CB长为半径的圆恰好经过AB的中点D,则AC的长为 .
【练能力】
12.在☉O中,直径AB=a,弦CD=b,则a与b大小为 ( )
A.a>b B.a≥b
C.a13.如图,OA是☉O的半径,B为OA上一点(且不与点O、A重合),过点B作OA的垂线交☉O于点C.以OB,BC为边作矩形OBCD,连接BD.若BD=10,BC=8,则AB的长为 ( )
A.8 B.6 C.4 D.2
14.如图,在☉O中,点A,O,D以及点B,O,C分别在一条直线上,则图中的弦有 ( )
A.2条 B.3条
C.4条 D.5条
15.东汉初年,我国的《周髀算经》里就有“径一周三”的古率,提出了圆的直径与周长之间存在一定的比例关系.将图中的半圆弧形铁丝向右水平拉直(保持M端不动),根据该古率,与拉直后铁丝N端的位置最接近的是 ( )
A.点A B.点B
C.点C D.点D
16.如图,在半圆O中,AB是直径,CD是一条弦,若AB=10,则△COD面积的最大值是 .
17.如图,在☉O中,C,D分别是半径OA,BO的中点,求证:AD=BC.
18.如图,AB是☉O的直径,CD是☉O的弦,AB,CD的延长线交于点E.已知AB=2DE,∠AEC=25°,求∠AOC的度数.
【练素养】
19.在☉O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在☉O上,且OP⊥PQ.
(1)如图1,当PQ∥AB时,求PQ的长度.
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
参考答案
练基础
1.A 2.D
3.【解析】如图,取AB的中点O,连接OC,OD.
∵△ABC和△ABD都为直角三角形,且∠ACB=∠ADB=90°,
∴DO,CO分别为Rt△ABD和Rt△ABC斜边上的中线,
∴OA=OB=OC=OD,
∴A,B,C,D四点在同一个圆上.
4.C 5.A 6.D
7.【解析】OA,OB,OC;AB,BC,AC;AC;, ,
8.D
9.【解析】∵BD=OD,∠B=38°,
∴∠DOB=∠B=38°,
∴∠ADO=∠DOB+∠B=2×38°=76°.
∵OA=OD,∴∠A=∠ADO=76°,
∴∠AOD=180°-∠A-∠ADO=180°-76°-76°=28°.
10.10° 11.5
练能力
12.B 13.C 14.B 15.A 16.12.5
17.【解析】∵OA,OB是☉O的两条半径,
∴AO=BO.
∵C,D分别是半径OA,BO的中点,
∴OC=OD.
在△ODA和△OCB中,
∴△ODA≌△OCB(SAS),
∴AD=BC.
18.【解析】如图,连接OD.
∵AB=2DE=2OD,
∴OD=DE.
又∵∠E=25°,
∴∠DOE=∠E=25°,
∴∠ODC=50°,
同理∠C=∠ODC=50°.
∴∠AOC=∠E+∠OCE=75°.
练素养
19.【解析】(1)如图1,连接OQ.
∵PQ∥AB,OP⊥PQ.∴OP⊥AB.
在Rt△OBP中,∵OB=AB=3,∠ABC=30°,
∴PB=2OP,由勾股定理可得OP=.
在Rt△OPQ中,PQ===.
(2)如图2,连接OQ,在Rt△OPQ中,PQ==,
∴当OP的长最小时,PQ的长最大.
此时OP⊥BC,则OP=OB=,
∴PQ长的最大值为==.
2
同课章节目录
