24.1.2 垂直于弦的直径 分层练习(含答案) 2023-2024学年数学人教版九年级上册
文档属性
| 名称 | 24.1.2 垂直于弦的直径 分层练习(含答案) 2023-2024学年数学人教版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 167.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 00:00:00 | ||
图片预览

文档简介
24.1.2 垂直于弦的直径
【练基础】
必备知识1 圆的对称性
1.下列说法中,不正确的是 ( )
A.圆既是轴对称图形又是中心对称图形
B.圆有无数条对称轴
C.圆的每一条直径都是它的对称轴
D.圆的对称中心是它的圆心
必备知识2 垂径定理及其推论
2.下列判断中正确的是 ( )
A.平分弦的直线垂直于弦
B.平分弦的直线也必平分弦所对的两条弧
C.弦的垂直平分线必平分弦所对的两条弧
D.平分一条弧的直线必平分这条弧所对的弦
3.在☉O中,直径AB=15,弦DE⊥AB于点C,若OC∶OB=3∶5,则DE的长为 ( )
A.6 B.9 C.12 D.15
4.如图,AB为☉O的直径,弦CD⊥AB于点H,若AB=10,CD=8,则BH的长度为 .
5.若☉O的半径为4 cm,弦AB=4 cm,则点O到AB的距离为 cm.
6.如图,☉O半径为10,P是弦AB上一动点,AB=16,则OP的取值范围是 .
必备知识3 垂径定理的应用
7.如图, 这是一座圆弧形拱桥,它的跨度(弧所对的弦长)24 m,拱高(弧的中点到弦的距离)4 m,则求拱桥的半径为 ( )
A.16 m B.20 m C.24 m D.28 m
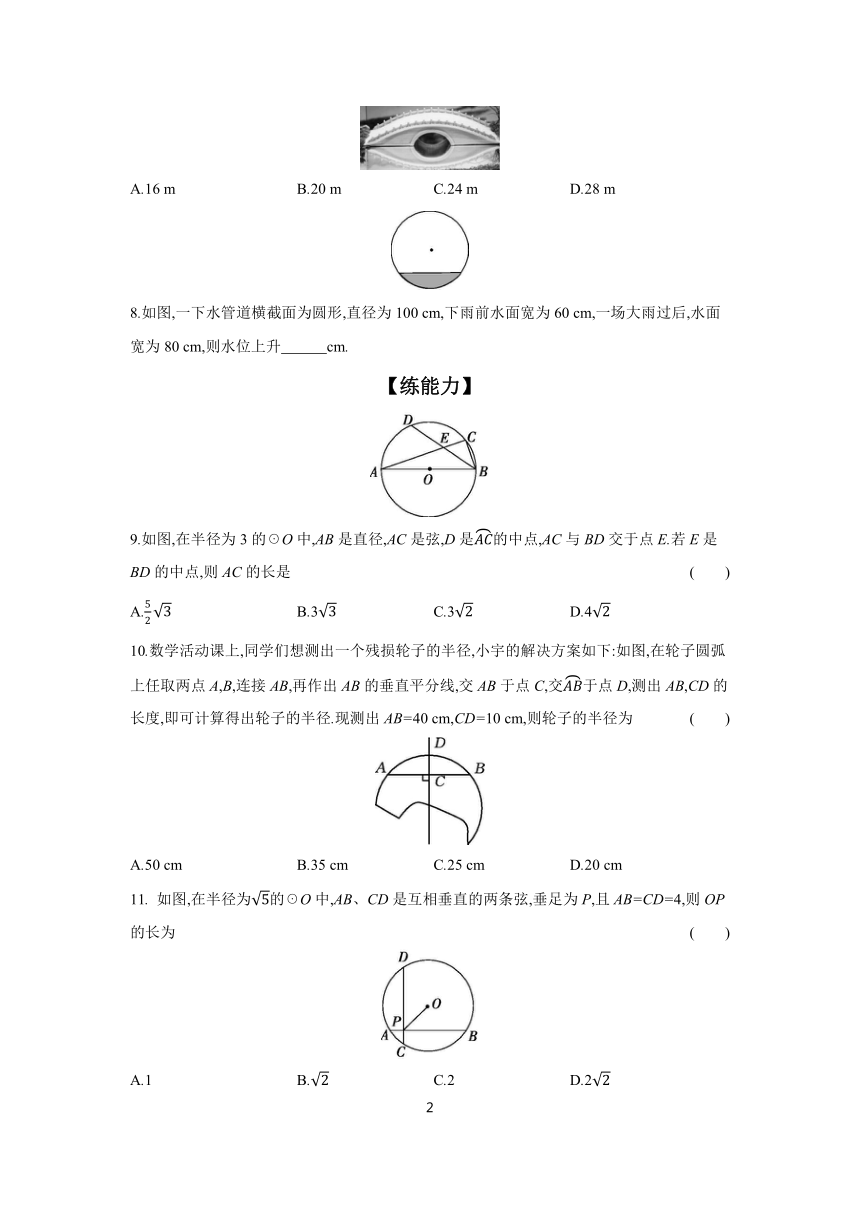
8.如图,一下水管道横截面为圆形,直径为100 cm,下雨前水面宽为60 cm,一场大雨过后,水面宽为80 cm,则水位上升 cm.
【练能力】
9.如图,在半径为3的☉O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是 ( )
A. B.3 C.3 D.4
10.数学活动课上,同学们想测出一个残损轮子的半径,小宇的解决方案如下:如图,在轮子圆弧上任取两点A,B,连接AB,再作出AB的垂直平分线,交AB于点C,交于点D,测出AB,CD的长度,即可计算得出轮子的半径.现测出AB=40 cm,CD=10 cm,则轮子的半径为 ( )
A.50 cm B.35 cm C.25 cm D.20 cm
11. 如图,在半径为的☉O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=4,则OP的长为 ( )
A.1 B. C.2 D.2
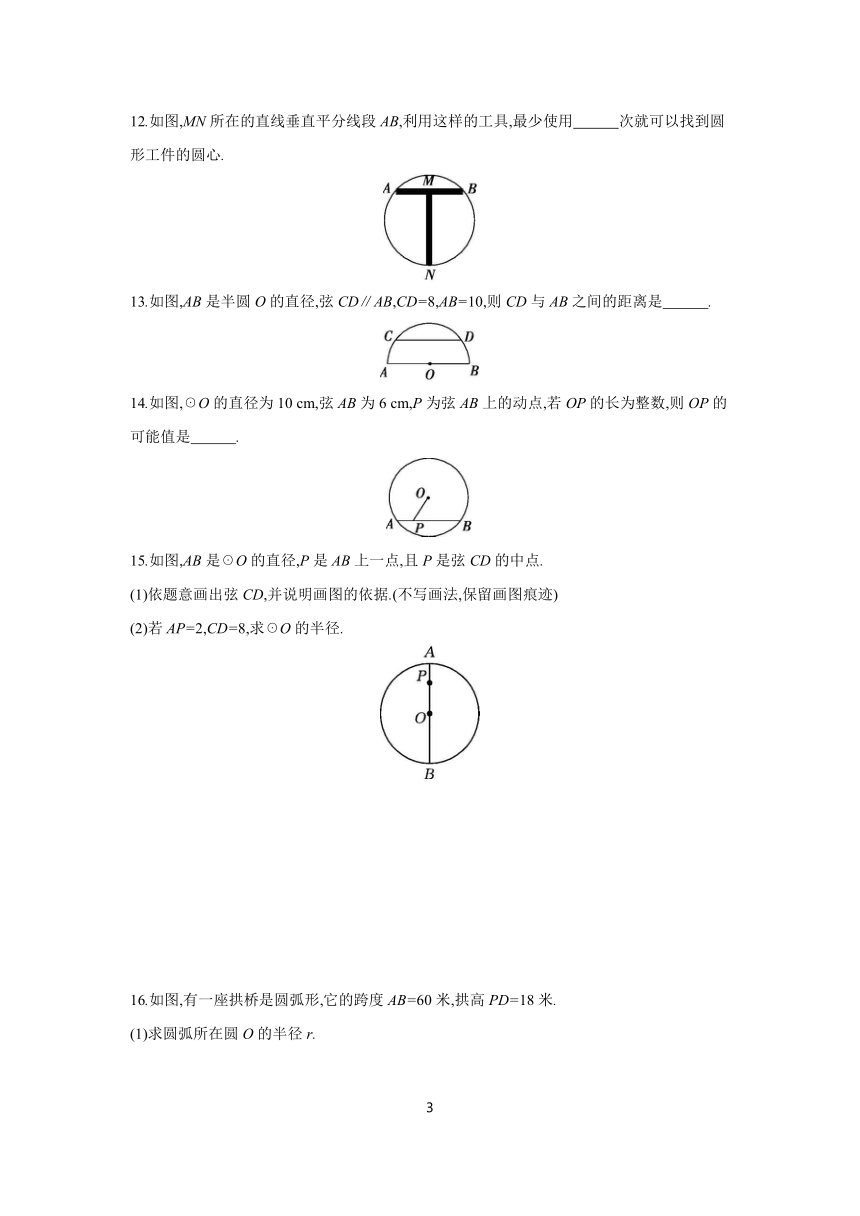
12.如图,MN所在的直线垂直平分线段AB,利用这样的工具,最少使用 次就可以找到圆形工件的圆心.
13.如图,AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是 .
14.如图,☉O的直径为10 cm,弦AB为6 cm,P为弦AB上的动点,若OP的长为整数,则OP的可能值是 .
15.如图,AB是☉O的直径,P是AB上一点,且P是弦CD的中点.
(1)依题意画出弦CD,并说明画图的依据.(不写画法,保留画图痕迹)
(2)若AP=2,CD=8,求☉O的半径.
16.如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在圆O的半径r.
(2)当洪水泛滥到跨度小于等于30米时,需要采取紧急措施.当拱顶离水面只有4米,即PE=4米时,是否需要采取紧急措施
【练素养】
17.如图,这是一张盾构隧道断面结构图.隧道内部是一个以O为圆心,AB为直径的圆.隧道内部共分为三层,上层为排烟道,中间为行车隧道,下层为服务层.点A到顶棚的距离为1.6 m,顶棚到路面的距离为6.4 m,点B到路面的距离为4.0 m.请求出路面CD的宽度.(精确到0.1 m)
参考答案
练基础
1.C 2.C 3.C 4.2 5.2 6.6≤OP≤10 7.B
8.10或70
练能力
9.D 10.C 11.B 12.2 13.3 14.4或5
15.【解析】(1)弦CD如图所示.
依据:平分弦(不是直径)的直径垂直于弦.
(2)如图,连接OD.
∵P是弦CD的中点,AB是☉O的直径,∴OA⊥CD,PD=CD.
∵CD=8,∴PD=4.
设☉O的半径为r,则OD=r,OP=OA-AP=r-2,
在Rt△ODP中,∠OPD=90°,
∴OD2=OP2+PD2,即r2=(r-2)2+42,解得r=5,
即☉O的半径为5.
16.【解析】(1)如图,连接OA,
由题意,得AD=AB=30米,OD=(r-18)米.
在Rt△ADO中,由勾股定理,得r2=302+(r-18)2,解得r=34.
故圆弧所在圆O的半径r为34米.
(2)如图,连接OA',
在Rt△OA'E中,OA'=34米,OE=OP-PE=30米,
由勾股定理,得A'E2=342-302,
∴A'E=16米,∴A'B'=32米.
∵32>30,∴不需要采取紧急措施.
练素养
17.【解析】如图,连接OC,设AB交CD于点E.
由题意知AB=1.6+6.4+4=12,
∴OC=OB=6 m,OE=OB-BE=6-4=2 m.
由题意可知AB⊥CD,
∵AB过点O,
∴CD=2CE.
在Rt△OCE中,由勾股定理得CE===4,
∴CD=2CE=8≈11.3 m.
∴路面CD的宽度为11.3 m.
2
【练基础】
必备知识1 圆的对称性
1.下列说法中,不正确的是 ( )
A.圆既是轴对称图形又是中心对称图形
B.圆有无数条对称轴
C.圆的每一条直径都是它的对称轴
D.圆的对称中心是它的圆心
必备知识2 垂径定理及其推论
2.下列判断中正确的是 ( )
A.平分弦的直线垂直于弦
B.平分弦的直线也必平分弦所对的两条弧
C.弦的垂直平分线必平分弦所对的两条弧
D.平分一条弧的直线必平分这条弧所对的弦
3.在☉O中,直径AB=15,弦DE⊥AB于点C,若OC∶OB=3∶5,则DE的长为 ( )
A.6 B.9 C.12 D.15
4.如图,AB为☉O的直径,弦CD⊥AB于点H,若AB=10,CD=8,则BH的长度为 .
5.若☉O的半径为4 cm,弦AB=4 cm,则点O到AB的距离为 cm.
6.如图,☉O半径为10,P是弦AB上一动点,AB=16,则OP的取值范围是 .
必备知识3 垂径定理的应用
7.如图, 这是一座圆弧形拱桥,它的跨度(弧所对的弦长)24 m,拱高(弧的中点到弦的距离)4 m,则求拱桥的半径为 ( )
A.16 m B.20 m C.24 m D.28 m
8.如图,一下水管道横截面为圆形,直径为100 cm,下雨前水面宽为60 cm,一场大雨过后,水面宽为80 cm,则水位上升 cm.
【练能力】
9.如图,在半径为3的☉O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是 ( )
A. B.3 C.3 D.4
10.数学活动课上,同学们想测出一个残损轮子的半径,小宇的解决方案如下:如图,在轮子圆弧上任取两点A,B,连接AB,再作出AB的垂直平分线,交AB于点C,交于点D,测出AB,CD的长度,即可计算得出轮子的半径.现测出AB=40 cm,CD=10 cm,则轮子的半径为 ( )
A.50 cm B.35 cm C.25 cm D.20 cm
11. 如图,在半径为的☉O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=4,则OP的长为 ( )
A.1 B. C.2 D.2
12.如图,MN所在的直线垂直平分线段AB,利用这样的工具,最少使用 次就可以找到圆形工件的圆心.
13.如图,AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是 .
14.如图,☉O的直径为10 cm,弦AB为6 cm,P为弦AB上的动点,若OP的长为整数,则OP的可能值是 .
15.如图,AB是☉O的直径,P是AB上一点,且P是弦CD的中点.
(1)依题意画出弦CD,并说明画图的依据.(不写画法,保留画图痕迹)
(2)若AP=2,CD=8,求☉O的半径.
16.如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在圆O的半径r.
(2)当洪水泛滥到跨度小于等于30米时,需要采取紧急措施.当拱顶离水面只有4米,即PE=4米时,是否需要采取紧急措施
【练素养】
17.如图,这是一张盾构隧道断面结构图.隧道内部是一个以O为圆心,AB为直径的圆.隧道内部共分为三层,上层为排烟道,中间为行车隧道,下层为服务层.点A到顶棚的距离为1.6 m,顶棚到路面的距离为6.4 m,点B到路面的距离为4.0 m.请求出路面CD的宽度.(精确到0.1 m)
参考答案
练基础
1.C 2.C 3.C 4.2 5.2 6.6≤OP≤10 7.B
8.10或70
练能力
9.D 10.C 11.B 12.2 13.3 14.4或5
15.【解析】(1)弦CD如图所示.
依据:平分弦(不是直径)的直径垂直于弦.
(2)如图,连接OD.
∵P是弦CD的中点,AB是☉O的直径,∴OA⊥CD,PD=CD.
∵CD=8,∴PD=4.
设☉O的半径为r,则OD=r,OP=OA-AP=r-2,
在Rt△ODP中,∠OPD=90°,
∴OD2=OP2+PD2,即r2=(r-2)2+42,解得r=5,
即☉O的半径为5.
16.【解析】(1)如图,连接OA,
由题意,得AD=AB=30米,OD=(r-18)米.
在Rt△ADO中,由勾股定理,得r2=302+(r-18)2,解得r=34.
故圆弧所在圆O的半径r为34米.
(2)如图,连接OA',
在Rt△OA'E中,OA'=34米,OE=OP-PE=30米,
由勾股定理,得A'E2=342-302,
∴A'E=16米,∴A'B'=32米.
∵32>30,∴不需要采取紧急措施.
练素养
17.【解析】如图,连接OC,设AB交CD于点E.
由题意知AB=1.6+6.4+4=12,
∴OC=OB=6 m,OE=OB-BE=6-4=2 m.
由题意可知AB⊥CD,
∵AB过点O,
∴CD=2CE.
在Rt△OCE中,由勾股定理得CE===4,
∴CD=2CE=8≈11.3 m.
∴路面CD的宽度为11.3 m.
2
同课章节目录
