2023-2024学年数学人教版九年级上册24.1.3 弧、弦、圆心角 分层练习(含解析)
文档属性
| 名称 | 2023-2024学年数学人教版九年级上册24.1.3 弧、弦、圆心角 分层练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 204.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 15:15:09 | ||
图片预览


文档简介
24.1.3 弧、弦、圆心角
【练基础】
必备知识1 圆心角的定义
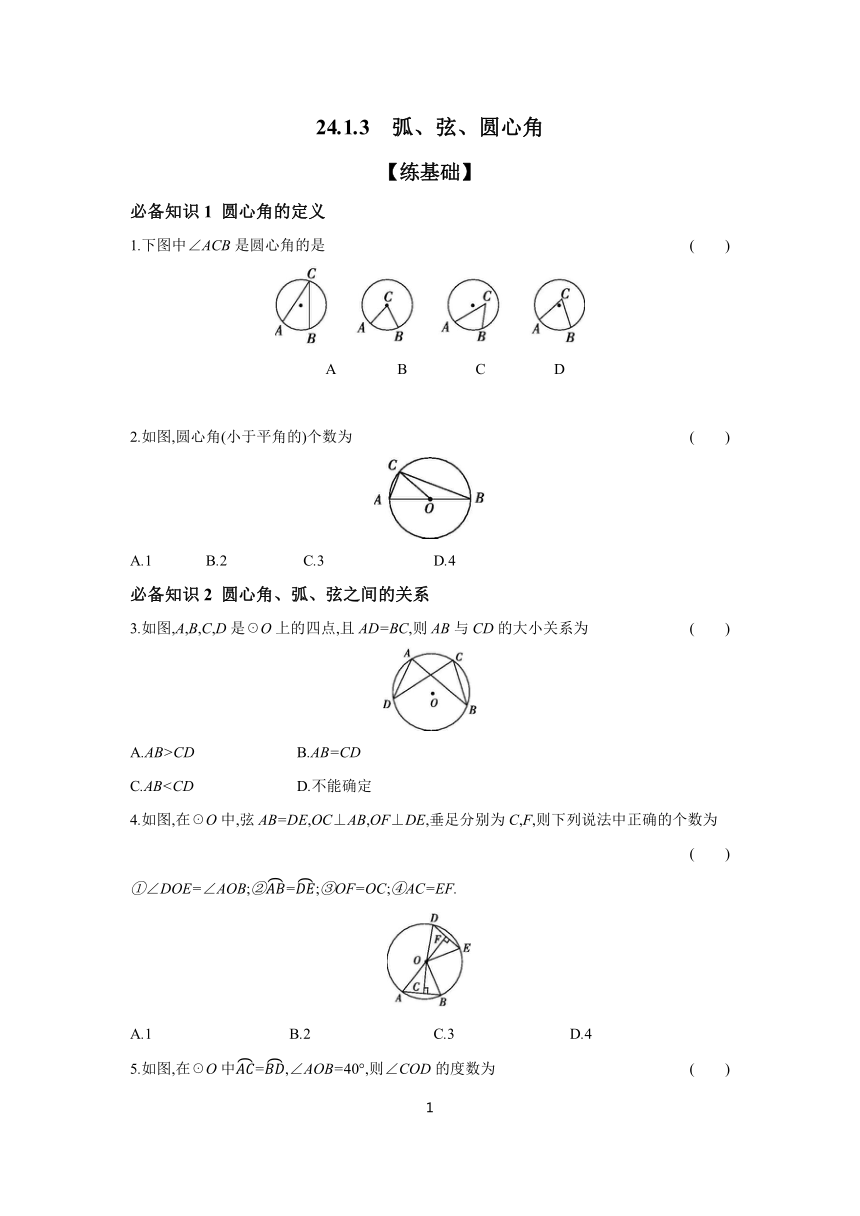
1.下图中∠ACB是圆心角的是 ( )
A B C D
2.如图,圆心角(小于平角的)个数为 ( )
A.1 B.2 C.3 D.4
必备知识2 圆心角、弧、弦之间的关系
3.如图,A,B,C,D是☉O上的四点,且AD=BC,则AB与CD的大小关系为 ( )
A.AB>CD B.AB=CD
C.AB4.如图,在☉O中,弦AB=DE,OC⊥AB,OF⊥DE,垂足分别为C,F,则下列说法中正确的个数为 ( )
①∠DOE=∠AOB;②=;③OF=OC;④AC=EF.
A.1 B.2 C.3 D.4
5.如图,在☉O中=,∠AOB=40°,则∠COD的度数为 ( )
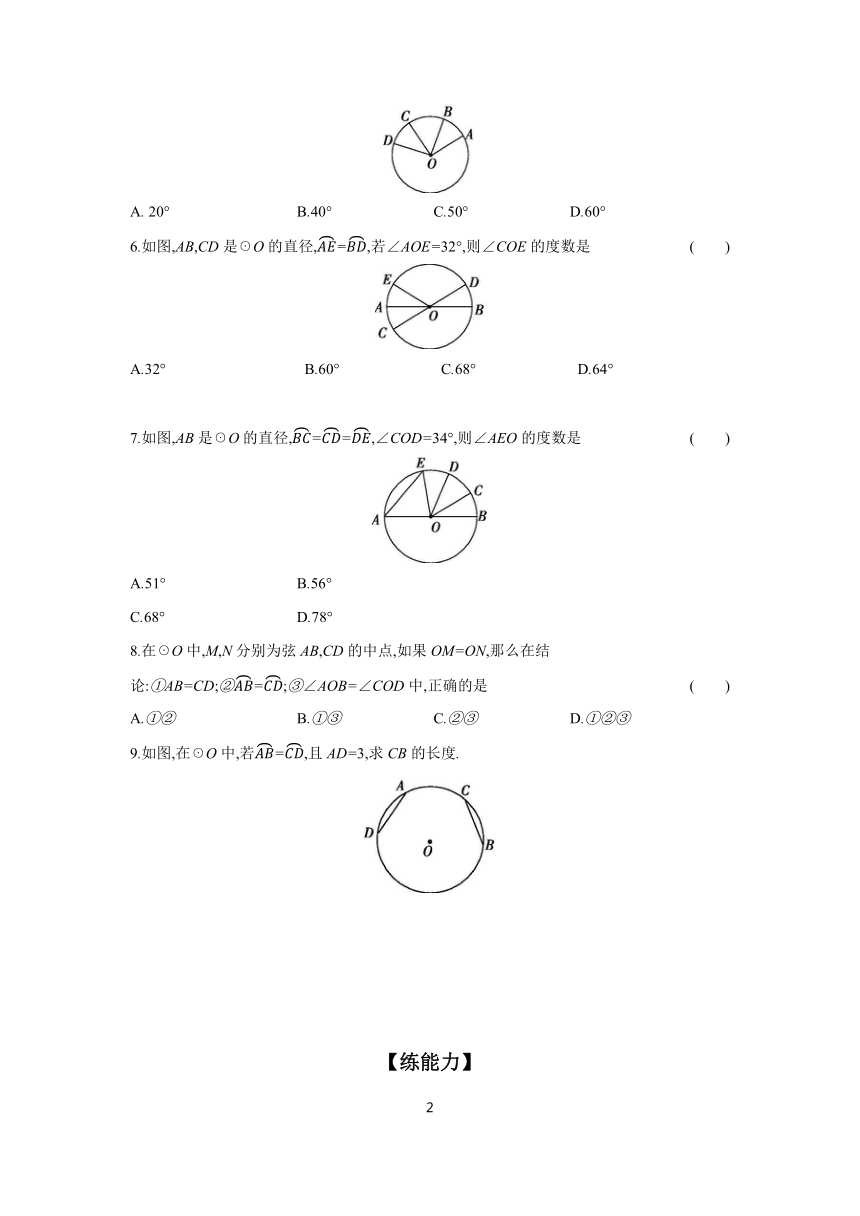
A. 20° B.40° C.50° D.60°
6.如图,AB,CD是☉O的直径,=,若∠AOE=32°,则∠COE的度数是 ( )
A.32° B.60° C.68° D.64°
7.如图,AB是☉O的直径,==,∠COD=34°,则∠AEO的度数是 ( )
A.51° B.56°
C.68° D.78°
8.在☉O中,M,N分别为弦AB,CD的中点,如果OM=ON,那么在结论:①AB=CD;②=;③∠AOB=∠COD中,正确的是 ( )
A.①② B.①③ C.②③ D.①②③
9.如图,在☉O中,若=,且AD=3,求CB的长度.
【练能力】
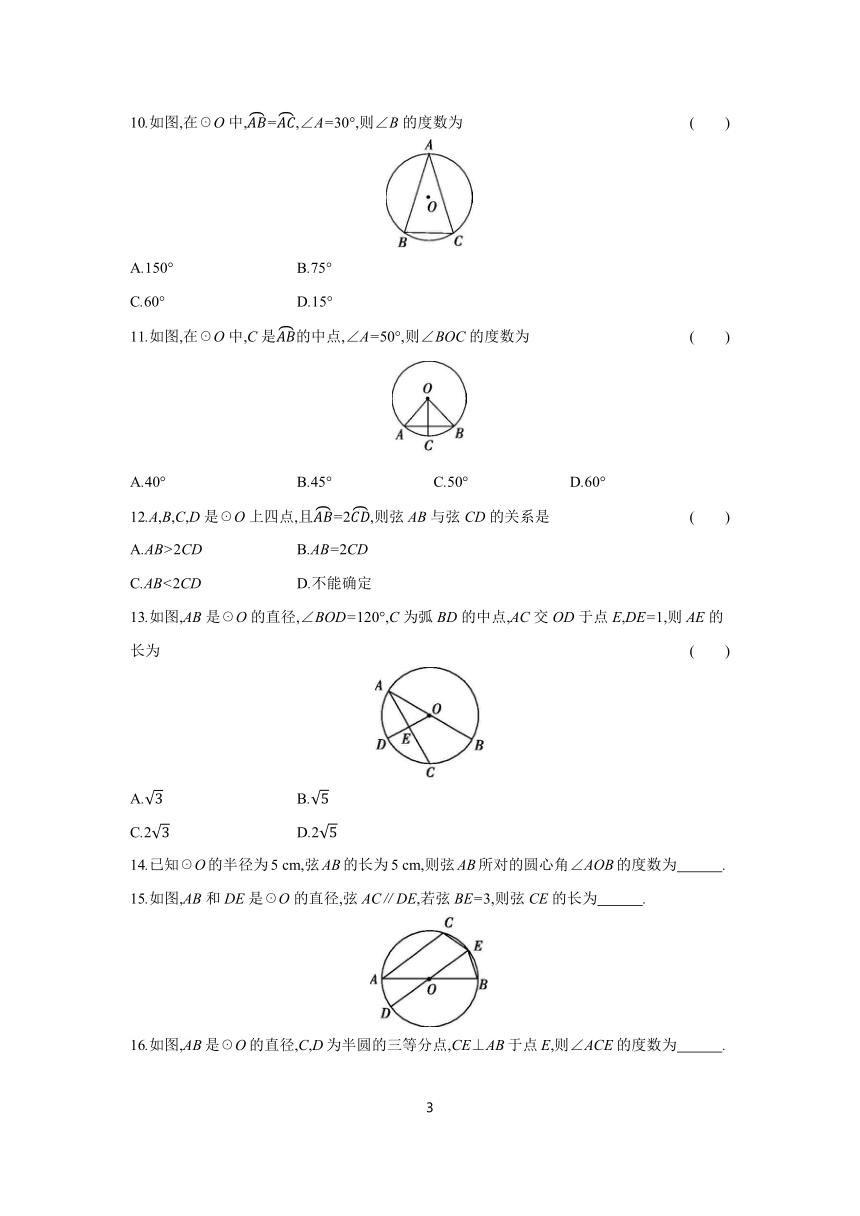
10.如图,在☉O中,=,∠A=30°,则∠B的度数为 ( )
A.150° B.75°
C.60° D.15°
11.如图,在☉O中,C是的中点,∠A=50°,则∠BOC的度数为 ( )
A.40° B.45° C.50° D.60°
12.A,B,C,D是☉O上四点,且=2,则弦AB与弦CD的关系是 ( )
A.AB>2CD B.AB=2CD
C.AB<2CD D.不能确定
13.如图,AB是☉O的直径,∠BOD=120°,C为弧BD的中点,AC交OD于点E,DE=1,则AE的长为 ( )
A. B.
C.2 D.2
14.已知☉O的半径为5 cm,弦AB的长为5 cm,则弦AB所对的圆心角∠AOB的度数为 .
15.如图,AB和DE是☉O的直径,弦AC∥DE,若弦BE=3,则弦CE的长为 .
16.如图,AB是☉O的直径,C,D为半圆的三等分点,CE⊥AB于点E,则∠ACE的度数为 .
17.如图,MB,MD是☉O的两条弦,点A,C分别在,上,且AB=CD,M是的中点.
(1)求证:MB=MD.
(2)过点O作OE⊥MB于点E,当OE=1,MD=4时,求☉O的半径.
18.如图,以 ABCD的顶点A为圆心,AB为半径作☉A,分别交BC,AD于E,F两点,交BA的延长线于点G,判断和是否相等,并说明理由.
【练素养】
19.如图,AB为☉O的弦,半径OC,OD分别交AB于点E,F.且=.
(1)求证:AE=BF.
(2)作半径ON⊥AB于点M,交☉O于点N,若AB=12,MN=3,求OM的长.
参考答案
练基础
1.B 2.B 3.B 4.D 5.B 6.D 7.A 8.D
9.【解析】∵=,
∴-=-,即=,
∴CB=AD=3.
练能力
10.B 11.A 12.C 13.A 14.60° 15.3 16.30°
17.【解析】(1)证明:∵AB=CD,
∴=.
∵M是的中点,
∴=,
∴=,
∴MB=DM.
(2)如图,连接OM.
∵DM=BM=4,OE⊥BM,
∴EM=BE=2.
∵OE=1,∠OEM=90°,
∴OM===,
∴☉O的半径为.
18.【解析】=.理由如下:
如图,连接AE,则AB=AE,
∴∠B=∠AEB.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠B=∠GAF,∠FAE=∠AEB,
∴∠GAF=∠FAE,∴=.
练素养
19.【解析】(1)证明:
如图1,连接OA,OB.
∵OA=OB,
∴∠A=∠B.
∵=,
∴∠AOE=∠BOF.
在△AOE和△BOF中,
∴△AOE≌△BOF(ASA),
∴AE=BF.
(2)如图2,连接OA.
∵OM⊥AB,
∴AM=AB=6.
设OM=x,则OA=ON=x+3.
在Rt△AOM中,由勾股定理得62+x2=(x+3)2,
解得x=4.5,
∴OM=4.5.
2
【练基础】
必备知识1 圆心角的定义
1.下图中∠ACB是圆心角的是 ( )
A B C D
2.如图,圆心角(小于平角的)个数为 ( )
A.1 B.2 C.3 D.4
必备知识2 圆心角、弧、弦之间的关系
3.如图,A,B,C,D是☉O上的四点,且AD=BC,则AB与CD的大小关系为 ( )
A.AB>CD B.AB=CD
C.AB
①∠DOE=∠AOB;②=;③OF=OC;④AC=EF.
A.1 B.2 C.3 D.4
5.如图,在☉O中=,∠AOB=40°,则∠COD的度数为 ( )
A. 20° B.40° C.50° D.60°
6.如图,AB,CD是☉O的直径,=,若∠AOE=32°,则∠COE的度数是 ( )
A.32° B.60° C.68° D.64°
7.如图,AB是☉O的直径,==,∠COD=34°,则∠AEO的度数是 ( )
A.51° B.56°
C.68° D.78°
8.在☉O中,M,N分别为弦AB,CD的中点,如果OM=ON,那么在结论:①AB=CD;②=;③∠AOB=∠COD中,正确的是 ( )
A.①② B.①③ C.②③ D.①②③
9.如图,在☉O中,若=,且AD=3,求CB的长度.
【练能力】
10.如图,在☉O中,=,∠A=30°,则∠B的度数为 ( )
A.150° B.75°
C.60° D.15°
11.如图,在☉O中,C是的中点,∠A=50°,则∠BOC的度数为 ( )
A.40° B.45° C.50° D.60°
12.A,B,C,D是☉O上四点,且=2,则弦AB与弦CD的关系是 ( )
A.AB>2CD B.AB=2CD
C.AB<2CD D.不能确定
13.如图,AB是☉O的直径,∠BOD=120°,C为弧BD的中点,AC交OD于点E,DE=1,则AE的长为 ( )
A. B.
C.2 D.2
14.已知☉O的半径为5 cm,弦AB的长为5 cm,则弦AB所对的圆心角∠AOB的度数为 .
15.如图,AB和DE是☉O的直径,弦AC∥DE,若弦BE=3,则弦CE的长为 .
16.如图,AB是☉O的直径,C,D为半圆的三等分点,CE⊥AB于点E,则∠ACE的度数为 .
17.如图,MB,MD是☉O的两条弦,点A,C分别在,上,且AB=CD,M是的中点.
(1)求证:MB=MD.
(2)过点O作OE⊥MB于点E,当OE=1,MD=4时,求☉O的半径.
18.如图,以 ABCD的顶点A为圆心,AB为半径作☉A,分别交BC,AD于E,F两点,交BA的延长线于点G,判断和是否相等,并说明理由.
【练素养】
19.如图,AB为☉O的弦,半径OC,OD分别交AB于点E,F.且=.
(1)求证:AE=BF.
(2)作半径ON⊥AB于点M,交☉O于点N,若AB=12,MN=3,求OM的长.
参考答案
练基础
1.B 2.B 3.B 4.D 5.B 6.D 7.A 8.D
9.【解析】∵=,
∴-=-,即=,
∴CB=AD=3.
练能力
10.B 11.A 12.C 13.A 14.60° 15.3 16.30°
17.【解析】(1)证明:∵AB=CD,
∴=.
∵M是的中点,
∴=,
∴=,
∴MB=DM.
(2)如图,连接OM.
∵DM=BM=4,OE⊥BM,
∴EM=BE=2.
∵OE=1,∠OEM=90°,
∴OM===,
∴☉O的半径为.
18.【解析】=.理由如下:
如图,连接AE,则AB=AE,
∴∠B=∠AEB.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠B=∠GAF,∠FAE=∠AEB,
∴∠GAF=∠FAE,∴=.
练素养
19.【解析】(1)证明:
如图1,连接OA,OB.
∵OA=OB,
∴∠A=∠B.
∵=,
∴∠AOE=∠BOF.
在△AOE和△BOF中,
∴△AOE≌△BOF(ASA),
∴AE=BF.
(2)如图2,连接OA.
∵OM⊥AB,
∴AM=AB=6.
设OM=x,则OA=ON=x+3.
在Rt△AOM中,由勾股定理得62+x2=(x+3)2,
解得x=4.5,
∴OM=4.5.
2
同课章节目录
