24.1.4 圆周角 分层练习(含答案) 2023-2024学年数学人教版九年级上册
文档属性
| 名称 | 24.1.4 圆周角 分层练习(含答案) 2023-2024学年数学人教版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 242.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-15 00:00:00 | ||
图片预览

文档简介
24.1.4 圆周角
【练基础】
必备知识1 圆周角的定义
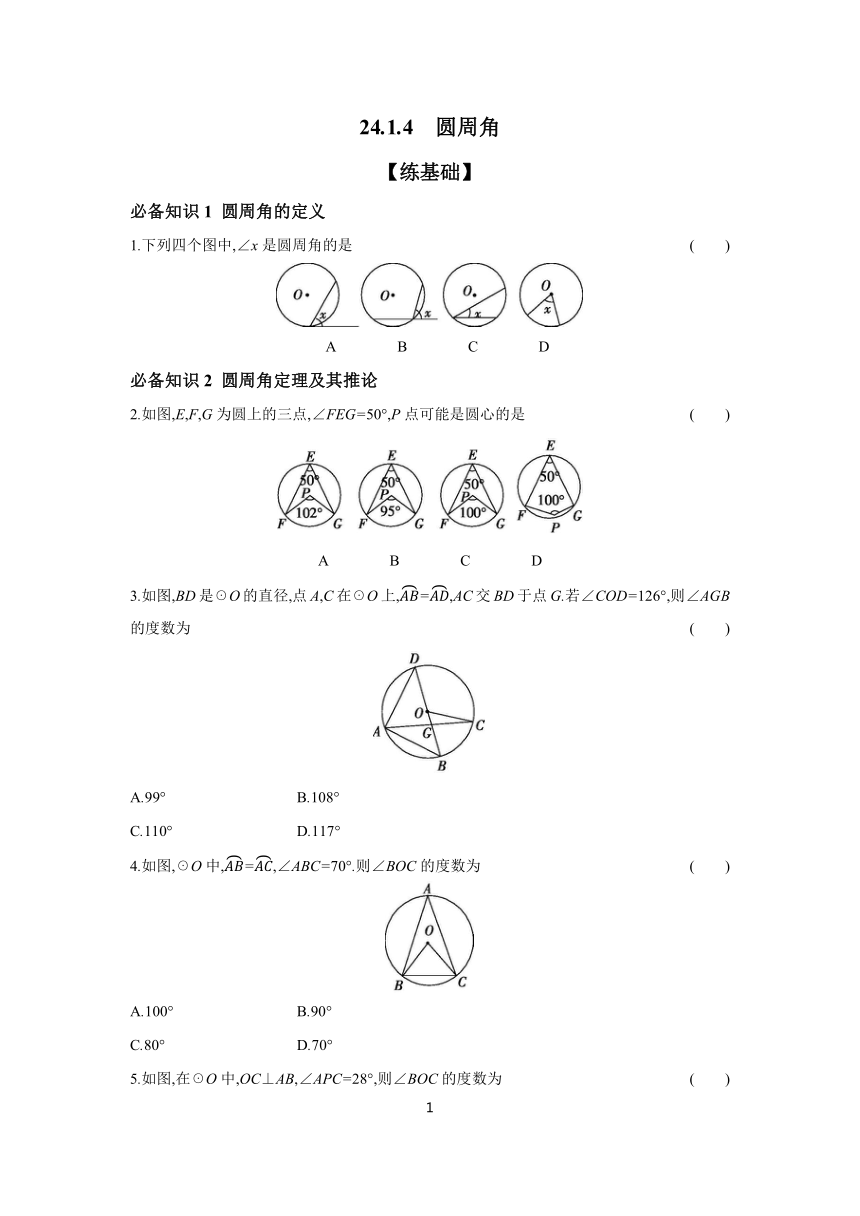
1.下列四个图中,∠x是圆周角的是 ( )
A B C D
必备知识2 圆周角定理及其推论
2.如图,E,F,G为圆上的三点,∠FEG=50°,P点可能是圆心的是 ( )
A B C D
3.如图,BD是☉O的直径,点A,C在☉O上,=,AC交BD于点G.若∠COD=126°,则∠AGB的度数为 ( )
A.99° B.108°
C.110° D.117°
4.如图,☉O中,=,∠ABC=70°.则∠BOC的度数为 ( )
A.100° B.90°
C.80° D.70°
5.如图,在☉O中,OC⊥AB,∠APC=28°,则∠BOC的度数为 ( )
A.14° B.28°
C.42° D.56°
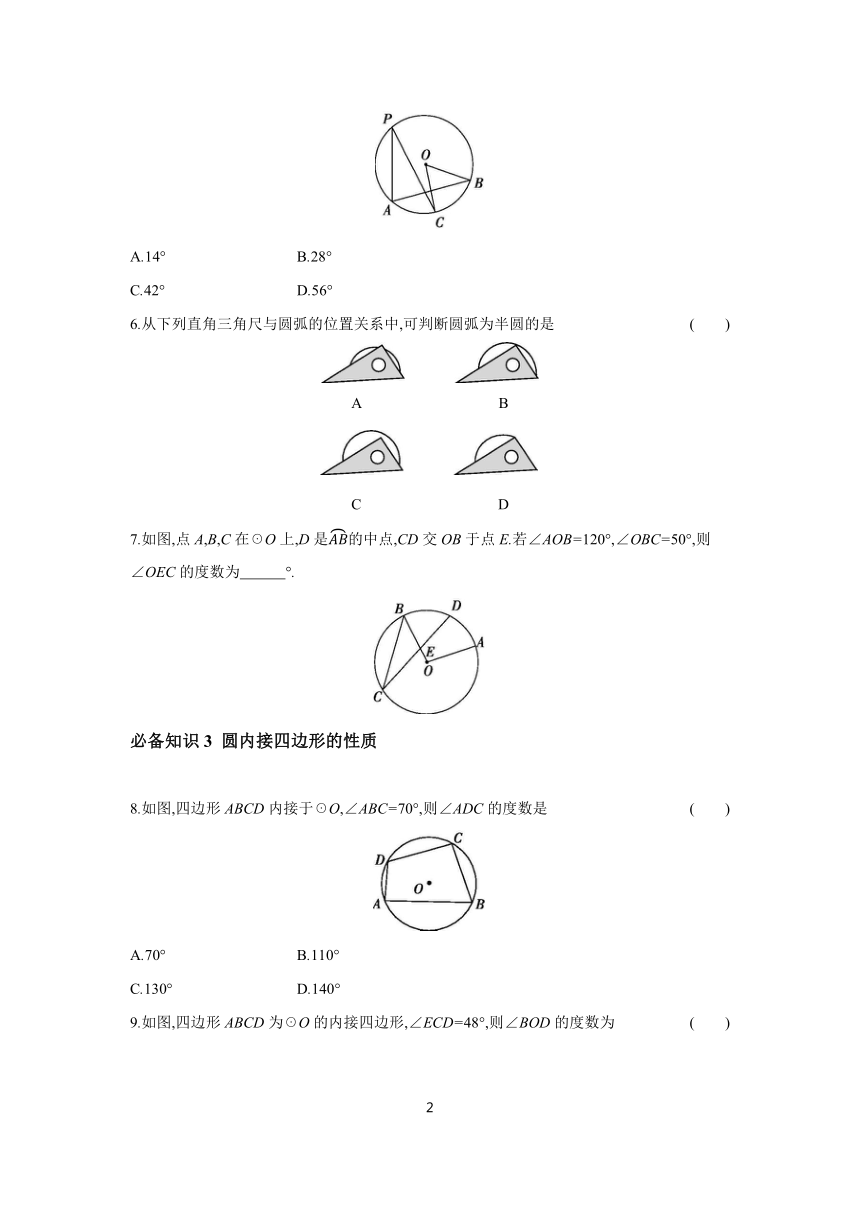
6.从下列直角三角尺与圆弧的位置关系中,可判断圆弧为半圆的是 ( )
A B
C D
7.如图,点A,B,C在☉O上,D是的中点,CD交OB于点E.若∠AOB=120°,∠OBC=50°,则∠OEC的度数为 °.
必备知识3 圆内接四边形的性质
8.如图,四边形ABCD内接于☉O,∠ABC=70°,则∠ADC的度数是 ( )
A.70° B.110°
C.130° D.140°
9.如图,四边形ABCD为☉O的内接四边形,∠ECD=48°,则∠BOD的度数为 ( )
A.48° B.96°
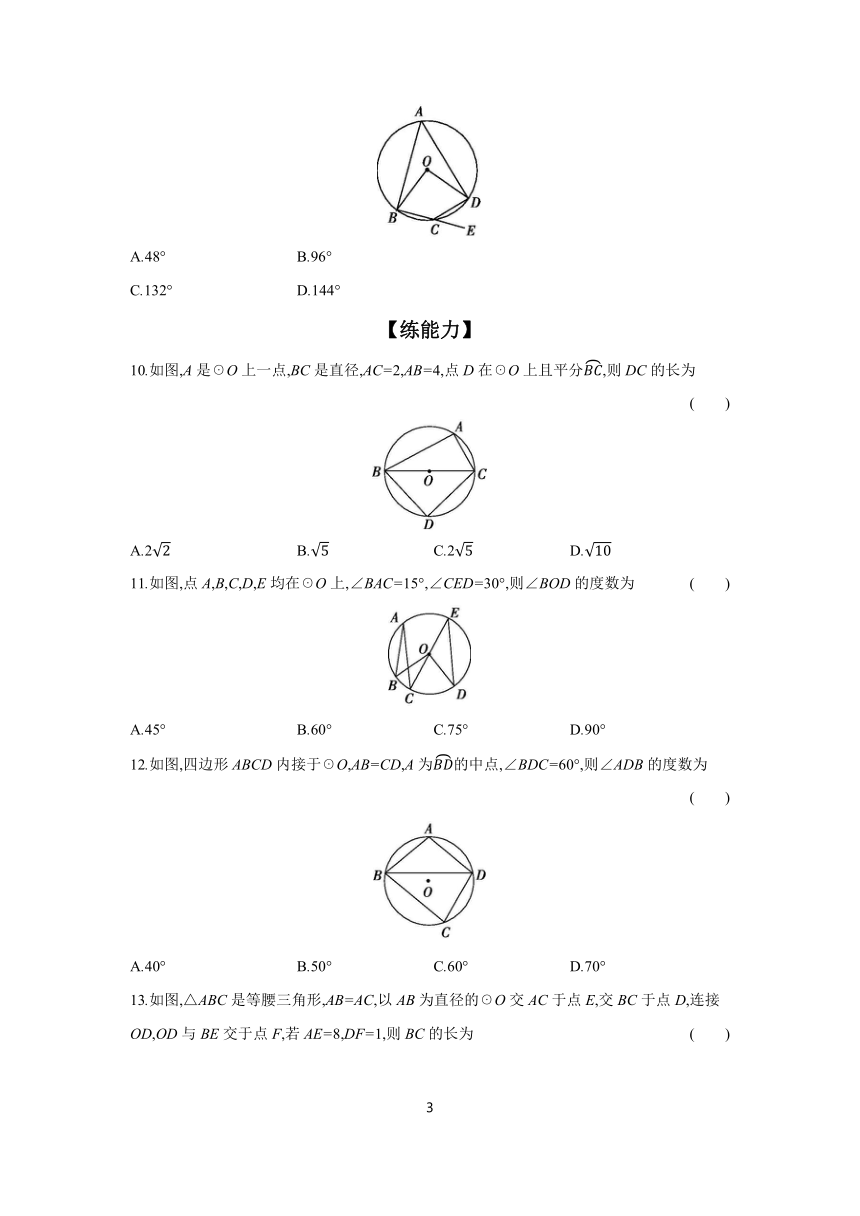
C.132° D.144°
【练能力】
10.如图,A是☉O上一点,BC是直径,AC=2,AB=4,点D在☉O上且平分,则DC的长为 ( )
A.2 B. C.2 D.
11.如图,点A,B,C,D,E均在☉O上,∠BAC=15°,∠CED=30°,则∠BOD的度数为 ( )
A.45° B.60° C.75° D.90°
12.如图,四边形ABCD内接于☉O,AB=CD,A为的中点,∠BDC=60°,则∠ADB的度数为 ( )
A.40° B.50° C.60° D.70°
13.如图,△ABC是等腰三角形,AB=AC,以AB为直径的☉O交AC于点E,交BC于点D,连接OD,OD与BE交于点F,若AE=8,DF=1,则BC的长为 ( )
A.2 B. C.6 D.2
14.如图,A,B,C是半径为4的☉O上的三个点,若∠BAC=45°,则弦BC的长等于 .
15.在☉O中,若弦BC垂直平分半径OA,则弦BC所对的圆周角的度数为 .
16.如图,A,B,C是☉O上的三个点,∠AOB=50°,∠B=55°,则∠A的度数为 .
17.如图,A,P,B,C是☉O上的四个点,∠APC=∠CPB=60°.
(1)判断△ABC的形状,并证明你的结论.
(2)证明:PA+PB=PC.
【练素养】
18.请阅读下列材料,并完成相应的任务.
克罗狄斯·托勒密(约90年-168年),古希腊天文学家、地理学家和光学家.在数学方面,他还论证了四边形的特性,即有名的托勒密定理,托勒密定理的内容如下:
圆的内接四边形的两条对角线的乘积等于两组对边乘积的和.如图1,若四边形ABCD内接于☉O,则有 .
任务:(1)材料中划横线部分应填写的内容为 .
(2)如图2,四边形ABCD内接于☉O,BD平分∠ABC,∠COD=120°,求证:BD=AB+BC.
参考答案
练基础
1.C 2.C 3.B 4.C 5.D 6.B 7.80 8.B 9.B
练能力
10.D 11.D 12.A 13.D 14.4 15.60°或120°
16.30°
17.【解析】(1)△ABC是等边三角形.
证明:由圆周角定理,得∠ABC=∠APC=60°,∠BAC=∠CPB=60°,
∴△ABC是等边三角形.
(2)证明:如图,在PC上截取PH=PA,连接AH.
∵∠APC=60°,
∴△APH为等边三角形,
∴AP=AH,∠AHP=60°.
在△APB和△AHC中,
∴△APB≌△AHC(AAS),
∴PB=HC,
∴PC=PH+HC=PA+PB,
即PA+PB=PC.
练素养
18.【解析】(1)AC·BD=AB·CD+BC·AD.
(2)证
明:如图,连接AC.
∵∠COD=120°,
∴∠CBD=∠CAD=60°.
∵BD平分∠ABC,
∴∠ABD=∠CBD=60°,
∴∠ACD=60°,
∴△ACD是等边三角形,
∴AC=AD=CD.
∵四边形ABCD是圆内接四边形,
∴AC·BD=AB·CD+BC·AD,
∴BD=AB+BC.
2
【练基础】
必备知识1 圆周角的定义
1.下列四个图中,∠x是圆周角的是 ( )
A B C D
必备知识2 圆周角定理及其推论
2.如图,E,F,G为圆上的三点,∠FEG=50°,P点可能是圆心的是 ( )
A B C D
3.如图,BD是☉O的直径,点A,C在☉O上,=,AC交BD于点G.若∠COD=126°,则∠AGB的度数为 ( )
A.99° B.108°
C.110° D.117°
4.如图,☉O中,=,∠ABC=70°.则∠BOC的度数为 ( )
A.100° B.90°
C.80° D.70°
5.如图,在☉O中,OC⊥AB,∠APC=28°,则∠BOC的度数为 ( )
A.14° B.28°
C.42° D.56°
6.从下列直角三角尺与圆弧的位置关系中,可判断圆弧为半圆的是 ( )
A B
C D
7.如图,点A,B,C在☉O上,D是的中点,CD交OB于点E.若∠AOB=120°,∠OBC=50°,则∠OEC的度数为 °.
必备知识3 圆内接四边形的性质
8.如图,四边形ABCD内接于☉O,∠ABC=70°,则∠ADC的度数是 ( )
A.70° B.110°
C.130° D.140°
9.如图,四边形ABCD为☉O的内接四边形,∠ECD=48°,则∠BOD的度数为 ( )
A.48° B.96°
C.132° D.144°
【练能力】
10.如图,A是☉O上一点,BC是直径,AC=2,AB=4,点D在☉O上且平分,则DC的长为 ( )
A.2 B. C.2 D.
11.如图,点A,B,C,D,E均在☉O上,∠BAC=15°,∠CED=30°,则∠BOD的度数为 ( )
A.45° B.60° C.75° D.90°
12.如图,四边形ABCD内接于☉O,AB=CD,A为的中点,∠BDC=60°,则∠ADB的度数为 ( )
A.40° B.50° C.60° D.70°
13.如图,△ABC是等腰三角形,AB=AC,以AB为直径的☉O交AC于点E,交BC于点D,连接OD,OD与BE交于点F,若AE=8,DF=1,则BC的长为 ( )
A.2 B. C.6 D.2
14.如图,A,B,C是半径为4的☉O上的三个点,若∠BAC=45°,则弦BC的长等于 .
15.在☉O中,若弦BC垂直平分半径OA,则弦BC所对的圆周角的度数为 .
16.如图,A,B,C是☉O上的三个点,∠AOB=50°,∠B=55°,则∠A的度数为 .
17.如图,A,P,B,C是☉O上的四个点,∠APC=∠CPB=60°.
(1)判断△ABC的形状,并证明你的结论.
(2)证明:PA+PB=PC.
【练素养】
18.请阅读下列材料,并完成相应的任务.
克罗狄斯·托勒密(约90年-168年),古希腊天文学家、地理学家和光学家.在数学方面,他还论证了四边形的特性,即有名的托勒密定理,托勒密定理的内容如下:
圆的内接四边形的两条对角线的乘积等于两组对边乘积的和.如图1,若四边形ABCD内接于☉O,则有 .
任务:(1)材料中划横线部分应填写的内容为 .
(2)如图2,四边形ABCD内接于☉O,BD平分∠ABC,∠COD=120°,求证:BD=AB+BC.
参考答案
练基础
1.C 2.C 3.B 4.C 5.D 6.B 7.80 8.B 9.B
练能力
10.D 11.D 12.A 13.D 14.4 15.60°或120°
16.30°
17.【解析】(1)△ABC是等边三角形.
证明:由圆周角定理,得∠ABC=∠APC=60°,∠BAC=∠CPB=60°,
∴△ABC是等边三角形.
(2)证明:如图,在PC上截取PH=PA,连接AH.
∵∠APC=60°,
∴△APH为等边三角形,
∴AP=AH,∠AHP=60°.
在△APB和△AHC中,
∴△APB≌△AHC(AAS),
∴PB=HC,
∴PC=PH+HC=PA+PB,
即PA+PB=PC.
练素养
18.【解析】(1)AC·BD=AB·CD+BC·AD.
(2)证
明:如图,连接AC.
∵∠COD=120°,
∴∠CBD=∠CAD=60°.
∵BD平分∠ABC,
∴∠ABD=∠CBD=60°,
∴∠ACD=60°,
∴△ACD是等边三角形,
∴AC=AD=CD.
∵四边形ABCD是圆内接四边形,
∴AC·BD=AB·CD+BC·AD,
∴BD=AB+BC.
2
同课章节目录
